Having attracted much attention in the past few years, predator-prey system provides a good mathematical model to present the correlation between predators and preys. This paper focuses on the robust stability of Lotka-Volterra predator-prey system with the fuzzy impulsive control model, and Takagi-Sugeno (T-S) fuzzy impulsive control model as well. Via the T-S model and the Lyapunov method, the controlling conditions of the asymptotical stability and exponential stability are established. Furthermore, the numerical simulation for the Lotka-Volterra predator-prey system with impulsive effects verifies the effectiveness of the proposed methods.

1. Introduction

Since Volterra presented the differential equation to solve the issue of the sharp change of the population of the sharks (predator) and the minions (prey) in 1925, the predator-prey system has been applied into many areas and played an important role in the biomathematics. Much attention has been attracted to the stability of the predator-prey system. Brauer and Soudack studied the global behavior of a predator-prey system under constant-rate prey harvesting with a pair of nonlinear ordinary differential equations [1]. Xu and his workmates concluded that a short-time delay could ensure the stability of the predator-prey system [2]. After analyzing the different capability between the mature and immature predator, Wang and his workmates obtained the global stability with the small time-delay system [3]. Li and his partners studied the impulsive control of Lotka-Volterra predator-prey system and established sufficient conditions of the asymptotic stability with the method of Lyapunov functions [4]. Liu and Zhang studied the coexistence and stability of predator-prey model with Beddington-DeAngelis functional response and stage structure [5]. Li did some work on the predator-prey system with Holling II functional response and obtained the existence, uniqueness and global asymptotic stability of the in random perturbation [6]. Furthermore, Ko and Ryu studied the qualitative behavior of nonconstant positive solutions on a general Gauss-type predator-prey model with constant diffusion rates under homogenous Neumann boundary condition [7]. Additionally, many papers discussed the predator-prey system with other different methods, such as LaSalle’s invariance principle method [8], Liu and Chen’s impulsive perturbations method [9], and Moghadas and Alexander’s generalized Gauss-type predator–prey model [10].

In recent years, fuzzy impulsive theory has been applied to the stability analysis of the non-linear differential equations [11–15]. However, it should be admitted that the stability of fuzzy logic controller (FLC) is still an open problem. It is well-known that the parallel distributed compensation technique has been the most popular controller design approach and belongs to a continuous input control way. It is important to point out that there exist many systems, like the predator-prey system, which cannot commonly endure continuous control inputs, or they have impulsive dynamical behavior due to abrupt jumps at certain instants during the evolving processes. In this sense, it is the same with communication networks, biological population management, chemical control, and so forth [16–23]. Hence, it is necessary to extend FLC and reflect these impulsive jump phenomena in the predator-prey system. Until recently, few papers talk about the stability of Lotka-Volterra predator-prey system with fuzzy impulsive control. In this paper, the writer will study the robustness of the predator-prey system by the fuzzy impulsive control based on the T-S mathematical model.

The rest of this paper is organized as follows. Section 2 describes the Lotka-Volterra predator-prey system and T-S fuzzy system with impulsive control. In Section 3, the theoretic analysis and design algorithm on stability of the impulsive fuzzy system are performed. Numerical simulations for the predator-prey system with impulsive effects are carried out with respect to the proposed method in Section 4. Finally, some conclusions are made in Section 5.

2. Problem Equation

The Lotka-Volterra predator-prey system is expressed with the following differential equation:

(2.1)

where x₁(t), x₂(t) (x₁(t) > 0, x₂(t) > 0) denote the species density of the preys and the predators in the group at time t respectively. The coefficient μ₁ > 0 denotes the birth rate of the preys, and μ₂ > 0 denotes the death rate of the predators. The other two coefficients r₁₂ and r₂₁ (both positive) describe interactions between the species.

In order to discuss the stability of the system, a matrix differential equation is presented as follows:

(2.2)

Lemma 2.1. , where x(t) ∈ Rⁿ is the state variable, and f ∈ C[Rⁿ, Rⁿ] satisfiesf(0) = 0, is a vector field defined over a compact region W⊆Rⁿ. By using the methods introduced in [24], one can construct fuzzy model for system (2.1) as follows.

Control Rule i (i = 1,2, …, r): IF z₁(t) is M_i1, z₂(t) is M_i2…, and z_p(t) is M_ip, THEN , where r is the number of T-S fuzzy rules, and z₁(t), z₂(t), …, z_p(t) are the premise variables, each M_ij (j = 1,2, …, p) is a fuzzy set, and A_i ∈ R^n×n is a constant matrix.

Thus, the nonlinear equation can be transformed to the following linear equation.

If x₂(t) is M_i

(2.3)

where

(2.4)

and d_i is related to the value of x₂(t) (here, d_i = x₂(t)). M_i, x(t), A_i ∈ R^{2 × 2}, r is the number of the IF-THEN rules, K_i,j ∈ R^{2 × 2} denotes the control of the j th impulsive instant,

Correspondently, with center-average defuzzifier, the overall T-S fuzzy impulsive system can be represented as follows:

(2.5)

where

and

Obviously, .

Lemma 2.2. If P is a real semipositive matrix, then a real matrix C exists, making P = C^TC.

3. Stability Analysis

Theorem 3.1. Assume that λ_i is the maximum eigenvalue of , let λ(α) = max _i {λ_i}, 0 < δ_j = τ_j − τ_j−1 < ∞ is impulsive distance [25]. If λ(α) ≥ 0 and there exists a constant scalar ε > 1 and a semipositive matrix P, such that

(3.1)

where

(3.2)

Then the system (2.5) is stable globally and asymptotically.

Proof. Let the candidate Lyapunov function be in the form of

(3.3)

Clearly, for t ≠ τ_j,

(3.4)

where t ∈ (τ_j−1, τ_j] (j = 1,2, …).

For t = τ_j, we have

(3.5)

Let j = 1, for any t ∈ (τ₀, τ₁], by (3.4), we obtain

(3.6)

Then

(3.7)

From (3.5) and (3.7), we obtain

(3.8)

In the same way, for any t ∈ (τ₁, τ₂], we have

(3.9)

Similarly, for all k and t ∈ (τ_k, τ_k+1], we obtain

(3.10)

From (3.2), we obtain

(3.11)

Thus, for t ∈ (τ_k, τ_k+1], k ∈ N, we have

(3.12)

So, if t → ∞, then k → ∞ and V(t, x) → 0. So the system (2.5) is stable globally and asymptotically.

Theorem 3.2. Assume that λ_i is the maximum eigenvalue of , let λ(α) = max _i {λ_i}, 0 < δ_j = τ_j − τ_j−1 < ∞ is impulsive distance. If λ(α) < 0 and a constant scalar 0 ≤ ε < −λ(α) exists, such that

(3.13)

where P = C^TC and β_j = max _i ∥C(I + K_i,j)∥.

Then the system (2.5) is stable globally and exponentially.

Proof. Let the candidate Lyapunov function be in the form of

(3.14)

Firstly, (3.4)–(3.10) hold.

From (3.13), we obtain

(3.15)

Thus, for t ∈ (τ_k, τ_k+1], k ∈ N,

(3.16)

Note that 0 ≤ ε < −λ(α), thus λ(α) + ε < 0. So the system (2.5) is stable globally and exponentially.

Next, we consider some special cases of the two theorems. Assume that K = K_i,j and σ = σ_j in the two theorems above, so we can have the following corollary.

Corollary 3.3. Let λ_i be the largest eigenvalue of [A + A^T], (i = 1,2, …, r), λ(α) = max _i {λ_i} > 0. If there exists a constant ε > 1 and a real semi-positive P such that

(3.17)

where P = C^TC, β_j = max _i ∥C(I + K_i,j)∥, and 0 < δ = τ_j − τ_j−1 < ∞ (j ∈ N) is impulsive distance. Then the system (2.5) is stable globally and asymptotically.

Corollary 3.4. Let λ_i be the largest eigenvalue of [A + A^T](i = 1,2, …, r), λ(α) = max _i {λ_i} < 0. If there exists a constant 0 ≤ ε < −λ(α) and a real semi-positive P such that

(3.18)

where P = C^TC, β_j = max _i ∥C(I + K_i,j)∥, and 0 < δ = τ_j − τ_j−1 < ∞(j ∈ N) is impulsive distance. Then the system (2.5) is stable globally and exponentially.

4. Numerical Simulation

In this section, we present a design example to show how to perform the impulsive fuzzy control on the Lotka-Volterra predator-prey systems with impulsive effects. Especially, the biological systems are very complex, nonlinear, and uncertain. As a result, they should be represented by fuzzy logical method with linguistic description.

Now, consider a predator-prey system with impulsive effects as follows:

(4.1)

where,

(4.2)

Solving From (2.3), we have the following impulsive fuzzy control for the above predator-prey model.

Rule i IF x₂(t) is M_i, then

(4.3)

where,

(4.4)

due to x₂(t)∈[0, d] = [0,0.12], and M₁(x₂(t)) = x₂(t)/d, M₂(x₂(t)) = −x₂(t)/d.

Let ε = 1.2, δ = 0.05, P = I, μ₁ = 0.2, μ₂ = 0.16, r₁₂ = 0.10, r₂₁ = 0.31.

From Theorem 3.1 and Corollary 3.3, we can get that λ(α) = 0.194.

Thus, we have chosen diag ([−0.82, − 0.82]) as impulsive control matrix, such that

(4.5)

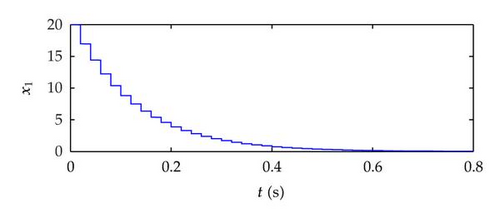
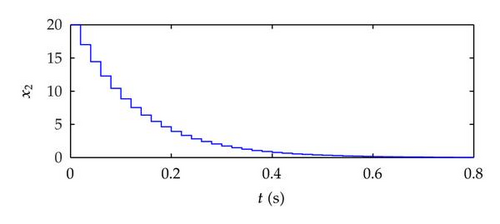
Thus, from Theorem 3.1 and Corollary 3.3, we can conclude that the numerical example is globally stable. The phase portrait of the system with impulsive control is shown in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The phase portrait of the system with fuzzy impulsive control.

5. Conclusions

The impulsive control technique, which was proved to be suitable for complex and nonlinear system with impulsive effects, was applied to analyzing the framework of the fuzzy systems based on T-S model and the proposed design approach. First, the robustness of the Lotka-Volterra predator-prey system based on the fuzzy impulsive control was carefully analyzed. Then, the overall impulsive fuzzy system was obtained by blending local linear impulsive system. Meanwhile, the asymptotical stability and exponential stability of the impulsive fuzzy system were derived by Lyapunov method. Finally, a numerical example for predator-prey systems with impulsive effects was given to illustrate the application of impulsive fuzzy control. The simulation results show that the proposed method was effective.

Acknowledgments

This work was supported by the National Natural Science Foundation of China, Project no. 50975300 and the Foundation of Education Department of Guangxi, China, Project no. 200808MS079.

References

1 Brauer F. and Soudack A. C., Stability regions in predator-prey systems with constant-rate prey harvesting, Journal of Mathematical Biology. (1979) 8, no. 1, 55–71, https://doi.org/10.1007/BF00280586, ZBL0406.92020.
10.1007/BF00280586
Web of Science® Google Scholar
2 Xu J., Pei L., and Lu Z., Lyapunov stability for a class of predator-prey model with delayed nutrient recycling, Chaos, Solitons and Fractals. (2006) 28, no. 1, 173–181, 2175552, https://doi.org/10.1016/j.chaos.2005.05.023, ZBL1125.34343.
10.1016/j.chaos.2005.05.023
Web of Science® Google Scholar
3 Wang W., Mulone G., Salemi F., and Salone V., Permanence and stability of a stage-structured predator-prey model, Journal of Mathematical Analysis and Applications. (2001) 262, no. 2, 499–528, 1859322, https://doi.org/10.1006/jmaa.2001.7543, ZBL0997.34069.
10.1006/jmaa.2001.7543
Web of Science® Google Scholar
4 Li D., Wang S., Zhang X., and Yang D., Impulsive control of uncertain Lotka-Volterra predator-prey system, Chaos, Solitons and Fractals. (2009) 41, no. 4, 1572–1577, 2537766, https://doi.org/10.1016/j.chaos.2008.06.021, ZBL1198.34092.
10.1016/j.chaos.2008.06.021
Web of Science® Google Scholar
5 Liu S. and Zhang J., Coexistence and stability of predator-prey model with Beddington-DeAngelis functional response and stage structure, Journal of Mathematical Analysis and Applications. (2008) 342, no. 1, 446–460, 2440811, https://doi.org/10.1016/j.jmaa.2007.12.038, ZBL1146.34057.
10.1016/j.jmaa.2007.12.038
Web of Science® Google Scholar
6 Li Y. and Gao H., Existence, uniqueness and global asymptotic stability of positive solutions of a predator-prey system with Holling II functional response with random perturbation, Nonlinear Analysis. Theory, Methods & Applications. (2008) 68, no. 6, 1694–1705, https://doi.org/10.1016/j.na.2007.01.008, 2388843, ZBL1143.34033.
10.1016/j.na.2007.01.008
Web of Science® Google Scholar
7 Ko W. and Ryu K., A qualitative study on general Gause-type predator-prey models with constant diffusion rates, Journal of Mathematical Analysis and Applications. (2008) 344, no. 1, 217–230, 2416302, https://doi.org/10.1016/j.jmaa.2008.03.006, ZBL1144.35029.
10.1016/j.jmaa.2008.03.006
Web of Science® Google Scholar
8 Hale J. K., Ordinary Differential Equations, 1969, Wiley-Interscience Press, New York, NY, USA, 0419901.
Google Scholar
9 Liu X. and Chen L., Complex dynamics of Holling type II Lotka-Volterra predator-prey system with impulsive perturbations on the predator, Chaos, Solitons and Fractals. (2003) 16, no. 2, 311–320, 1949478, https://doi.org/10.1016/S0960%2D0779(02)00408%2D3, ZBL1085.34529.
10.1016/S0960-0779(02)00408-3
Web of Science® Google Scholar
10 Moghadas S. M. and Alexander M. E., Dynamics of a generalized Gause-type predator-prey model with a seasonal functional response, Chaos, Solitons and Fractals. (2005) 23, no. 1, 55–65, https://doi.org/10.1016/j.chaos.2004.04.030, ZBL1058.92049.
10.1016/j.chaos.2004.04.030
Web of Science® Google Scholar
11 Liu B., Chen G., Teo K. L., and Liu X., Robust global exponential synchronization of general Lur′e chaotic systems subject to impulsive disturbances and time delays, Chaos, Solitons and Fractals. (2005) 23, no. 5, 1629–1641, https://doi.org/10.1016/j.chaos.2004.06.050, 2101578.
10.1016/j.chaos.2004.06.050
Web of Science® Google Scholar
12 Chuang C.-F., Wang W.-J., and Chen Y.-J., H_∞ synchronization of fuzzy model based chen chaotic systems, Proceedings of the IEEE International Conference on Control Applications (CCA ′10), September 2010, 1199–1204, 2-s2.0-78649409621, https://doi.org/10.1109/CCA.2010.5611325.
10.1109/CCA.2010.5611325
Google Scholar
13 Park C.-W., Lee C.-H., and Park M., Design of an adaptive fuzzy model based controller for chaotic dynamics in Lorenz systems with uncertainty, Information Sciences. (2002) 147, no. 1-4, 245–266, https://doi.org/10.1016/S0020%2D0255(02)00271%2D2, 1940753, ZBL1008.93512.
10.1016/S0020-0255(02)00271-2
Web of Science® Google Scholar
14 Guan X. P. and Hua C. C., Synchronization of uncertain time delay chaotic systems using the adaptive fuzzy method, Chinese Physics Letters. (2002) 19, no. 8, 1031–1034, 2-s2.0-0036679014, https://doi.org/10.1088/0256%2D307X/19/8/301.
10.1088/0256-307X/19/8/301
Web of Science® Google Scholar
15 Dong L., Shi-long W., Xiao-Hong Z., Yang D., and Wang H., Fuzzy impulsive control of permanent magnet synchronous motors, Chinese Physics Letters. (2008) 25, no. 2, 401–404, 2-s2.0-42649123973, https://doi.org/10.1088/0256%2D307X/25/2/014.
10.1088/0256-307X/25/2/014
Web of Science® Google Scholar
16 Xiang Z. and Chen G., Stability analysis and robust H_∞ control of switched stochastic systems with time-varying delay, Journal of Applied Mathematics. (2012) 2012, 17, 202916, https://doi.org/10.1155/2012/202916.
10.1155/2012/202916
Google Scholar
17 Guan Z.-H., Liao R.-Q., Zhou F., and Wang H. O., On impulsive control and its application to Chen′s chaotic system, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2002) 12, no. 5, 1191–1197, 1913998, ZBL1051.93508, https://doi.org/10.1142/S0218127402005030.
10.1142/S0218127402005030
Web of Science® Google Scholar
18 Tang S. Y. and Chen L. S., Multiple attractors in stage-structured population models with birth pulses, Bulletin of Mathematical Biology. (2003) 65, no. 3, 479–495, 2-s2.0-0037406610, https://doi.org/10.1016/S0092%2D8240(03)00005%2D3.
10.1016/S0092-8240(03)00005-3
PubMed Web of Science® Google Scholar
19 Xiang S. Y., Pan W., Yan L., Luo B., Jiang N., and Wen K., Using polarization properties to enhance performance of chaos synchronization communication between vertical-cavity surface-emitting lasers, Optics and Laser Technology. (2010) 42, no. 4, 674–681, 2-s2.0-73249122858, https://doi.org/10.1016/j.optlastec.2009.11.010.
10.1016/j.optlastec.2009.11.010
CAS Web of Science® Google Scholar
20 Tang S. Y. and Chen L., Density-dependent birth rate, birth pulses and their population dynamic consequences, Journal of Mathematical Biology. (2002) 44, no. 2, 185–199, 1889910, https://doi.org/10.1007/s002850100121, ZBL0990.92033.
10.1007/s002850100121
PubMed Web of Science® Google Scholar
21 Li X., Rakkiyappan R., and Balasubramaniam P., Existence and global stability analysis of equilibrium of fuzzy cellular neural networks with time delay in the leakage term under impulsive perturbations, Journal of the Franklin Institute. (2011) 348, no. 2, 135–155, https://doi.org/10.1016/j.jfranklin.2010.10.009, 2771833.
10.1016/j.jfranklin.2010.10.009
Web of Science® Google Scholar
22 Rakkiyappan R. and Balasubramaniam P., On exponential stability results for fuzzy impulsive neural networks, Fuzzy Sets and Systems. (2010) 161, no. 13, 1823–1835, https://doi.org/10.1016/j.fss.2009.12.016, 2610673, ZBL1198.34160.
10.1016/j.fss.2009.12.016
Web of Science® Google Scholar
23 Martynyuk A. A., Stability in the models of real world phenomena, Nonlinear Dynamics and Systems Theory. (2011) 11, no. 1, 7–52, 2798814.
Google Scholar
24 Tanaka K. and Wang H., Fuzzy Control Systems Design and Analysis, a Linear Matrix Inequality Approach, 2001, Wiley, New York, NY, USA.
10.1002/0471224596
Google Scholar
25 Wang Y., Honglin Y. U., Zhang X., and Li D., Stability analysis and design of time-varying nonlinear systems based on impulsive fuzzy model, Discrete Dynamics in Nature and Society. (2012) 2012, 16, 192546, https://doi.org/10.1155/2012/192546.
10.1155/2012/192546
Web of Science® Google Scholar

Citing Literature

All articles

Stability Analysis of Predator-Prey System with Fuzzy Impulsive Control

Abstract

1. Introduction

2. Problem Equation

3. Stability Analysis

4. Numerical Simulation

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Stability Analysis of Predator-Prey System with Fuzzy Impulsive Control

Abstract

1. Introduction

2. Problem Equation

3. Stability Analysis

4. Numerical Simulation

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information