This paper is concerned with the finite-time H_∞ filtering problem for linear continuous time-varying systems with uncertain observations and ℒ₂-norm bounded noise. The design of finite-time H_∞ filter is equivalent to the problem that a certain indefinite quadratic form has a minimum and the filter is such that the minimum is positive. The quadratic form is related to a Krein state-space model according to the Krein space linear estimation theory. By using the projection theory in Krein space, the finite-time H_∞ filtering problem is solved. A numerical example is given to illustrate the performance of the H_∞ filter.

1. Introduction

Most of the literatures on estimation problem always assume the observations contain the signal to be estimated [1–8]. In [5], the linear matrix inequality technique was applied to solve the finite-time H_∞ filtering problem of singular Markovian jump systems. In [6], new stability and robust stability results for 2D discrete stochastic systems were proposed based on weaker conservative assumptions. In [7], an observer was incorporated to the vaccination control rule for an SEIR propagation disease model. In [8], two linear observer prototypes for a class of linear hybrid systems were proposed based on the prediction error. However, in practice, the observation may contain the signal in a random manner, that is, the observation consists of noise alone in a nonzero probability, and it is commonly called uncertain observations or missing measurements [9, 10]. In this paper, the finite-time H_∞ filtering problem is investigated for linear continuous time-varying systems with uncertain observations and ℒ₂-norm bounded noises.

The H₂-based optimal filtering has been well studied for linear systems with uncertain observations [9–13]. In [9], the recursive least-squares estimator was proposed for linear discrete-time systems with uncertain observations. The robust optimal filter for discrete time-varying systems with missing measurements and norm-bounded parameter uncertainties was designed by optimizing the upper bound of the state estimation error variance in [10]. Using the covariance information, the recursive least-squares filtering and fixed-point smoothing algorithms for linear continuous-time systems with uncertain observations were proposed in [11]. Linear and nonlinear one-step prediction algorithms for discrete-time systems with uncertain observations were presented from a covariance assignment viewpoint in [12]. The statistical convergence properties of the estimation error covariance were studied, and the existence of a critical value for the arrival rate of the observations was shown in [13]. In recent years, due to the fact that the H_∞-based estimation approach does not require the information on statistics of input noise, it has received more and more attention for linear systems with uncertain observations [14–16]. Using Lyapunov function approach, the H_∞ filtering algorithms in terms of linear matrix inequalities were proposed for systems with missing measurements in [14–16]. To authors’ best knowledge, research on finite-time H_∞ filtering for linear continuous time-varying systems with uncertain observations has not been fully investigated and remains to be challenging, which motivates the present study.

Although the Krein space linear estimation theory [1, 3] has been applied to fault detection and nonlinear estimation [17, 18], no results have been developed for systems with uncertain observations, which will be an interesting research topic in the future. In this paper, the problem of finite-time H_∞ filtering will be investigated for linear continuous time-varying systems with uncertain observations and ℒ₂-norm bounded input noise. Based on the knowledge of Krein space linear estimation theory [1, 3], a new approach in Krein space will be developed to handle the H_∞ filtering problem for linear continuous time-varying systems with uncertain observations. It will be shown that the H_∞ filtering problem for linear continuous time-varying systems with uncertain observations is partially equivalent to an H₂ filtering problem for a certain Krein space state-space model. Through employing projection theory, both the existence condition and a solution of the H_∞ filtering can be obtained in terms of a differential Riccati equation. The major contribution of this paper can be summarized as follows: (i) it shows that the H_∞ filtering problem for systems with uncertain observations can be converted into an H₂ optimal estimation problem subject to a fictitious Krein space stochastic systems; (ii) it develops a Kalman-like robust estimator for linear continuous time-varying systems with uncertain observations.

Notation. Elements in a Krein space will be denoted by boldface letters, and elements in the Euclidean space of complex numbers will be denoted by normal letters. The superscripts “−1” and “*” stand for the inverse and complex conjugation of a matrix, respectively. δ(t − τ) = 0 for t ≠ τ and δ(t − τ) = 1 for t = τ. ℝⁿ denotes the n-dimensional Euclidean space. I is the identity matrix with appropriate dimensions. For a real matrix, P > 0 (resp., P < 0) means that P is symmetric and positive (resp., negative) definite. 〈·, ·〉 denotes the inner product in Krein space. diag {⋯} denotes a block-diagonal matrix. θ(t) ∈ ℒ₂[0, T] means . ℒ{⋯} denotes the linear space spanned by sequence {⋯}. An abstract vector space {𝒦, 〈·, ·〉} that satisfies the following requirements is called a Krein space [1].

(i)
𝒦 is a linear space over 𝒞, the field of complex numbers.
(ii)
There exists a bilinear form 〈·, ·〉∈𝒞 on 𝒦 such that
(a)
〈y, x〉 = 〈x, y〉 ^*,
(b)
〈ax + by, z〉 = a〈x, z〉+b〈y, z〉,
for any x, y, z ∈ 𝒦, a, b ∈ 𝒞, and where * denotes complex conjugation.
(iii)
The vector space 𝒦 admits a direct orthogonal sum decomposition
()
such that {𝒦₊, 〈·, ·〉} and {𝒦₋, −〈·, ·〉} are Hilbert spaces, and
()
for any x ∈ 𝒦₊ and y ∈ K₋.

2. System Model and Problem Formulation

In this paper, we consider the following linear continuous time-varying system with uncertain observations

()

where x(t) ∈ ℝⁿ is the state vector, w(t) ∈ ℝ^p is an exogenous disturbance belonging to ℒ₂[0, T], y(t) ∈ ℝ^m is the observation, v(t) ∈ ℝ^m is the observation noise belonging to ℒ₂[0, T], z(t) ∈ ℝ^q is the signal to be estimated, and A(t), B(t), C(t), and L(t) are known real time-varying matrices with appropriate dimensions.

The stochastic variable r(t) ∈ ℝ takes the values of 0 and 1 with

()

[11]. Note that many literatures associated with observer design are based on the assumption that p(t) = 1 [1–4], it can be unreasonable in many practical applications [9, 10, 13]. In this paper, we assume that p(t) is a known positive scalar.

The finite-time H_∞ filtering problem under investigation is stated as follows: given a scalar γ > 0, a matrix P₀ > 0, and the observation {y(s)|_0≤s≤t}, find an estimate of the signal z(t), denoted by

, such that

()

where

Thus, the finite-time H_∞ filtering problem can be equivalent to the following:

(I)
J_ℱ has a minimum with respect to ;
(II)
can be chosen such that the value of J_ℱ at its minimum is positive.

3. Main Results

In this section, through introducing a fictitious Krein space-state space model, we construct a partially equivalent Krein space projection problem. By using innovation analysis approach, we derive the finite-time H_∞ filter and its existence condition.

3.1. Construct a Partially Equivalent Krein Space Problem

To begin with, we introduce the following state transition matrix:

()

it follows from the state-space model (2.1) that

()

Thus, we can rewrite J_ℱ as

()

where

()

Moreover, we introduce the following Krein space stochastic system

()

where x₀, w(t), v(t), v_s(t), and e_f(t) are mutually uncorrelated white noises with zero means and known covariance matrices as

()

Let

()

then it follows from (3.1), (3.3), (3.4), and (3.7) that

()

According to [1] and [3], we have the following results.

Lemma 3.1. Consider system (2.1), given a scalar γ > 0 and a matrix P₀ > 0, then J_ℱ in (2.3) has the minimum over {x₀, w(t)|_0≤t≤T} if and only if the innovation exists for 0 ≤ t ≤ T, where

()

, and

denote the projection of y_z(t) onto

. In this case the minimum value of J_ℱ is

()

where

is obtained from the Krein space projection of x(t) onto ℒ{{y_z(j)}|_0≤τ<t}.

Remark 3.2 3.2. By analyzing the indefinite quadratic form J_ℱ in (3.4) and using the Krein space linear estimation theory [1], it has been shown that the H_∞ filtering problem for linear systems with uncertain observations is equivalent to the H₂ estimation problem with respect to a Krein space stochastic system, which is new as far as we know. In this case, Krein space projection method can be applied to derive an H_∞ estimator for linear systems with uncertain observations, which is more simple and intuitive than previous versions.

3.2. Solution of the Finite-Time H_∞ Filtering Problem

By applying the standard Kalman filter formula to system (3.6), we have the following lemma.

Lemma 3.3. Consider the Krein space stochastic system (3.6), the prediction is calculated by

()

where

()

and P(t) is computed by

()

Now we are in the position to present the main results of this subsection.

Theorem 3.4 3.4. Consider system (2.1), given a scalar γ > 0 and a matrix P₀ > 0, and suppose P(t) is the bounded positive definite solution to Riccati differential equation (3.14). Then, one possible level-γ finite-time H_∞ filter that achieves (2.3) is given by

()

where

()

with

Proof. It follows from Lemma 3.3 that if P(t) is a bounded positive definite solution to Riccati differential equation (3.14), then the projection exists. According to Lemma 3.1, it is obvious that the H_∞ filter that achieves (2.3) exists. If this is the case, the minimum value of J_ℱ is given by (3.11). In order to achieve min J_ℱ > 0, one natural choice is to set

()

thus the finite-time H_∞ filter can be given by (3.15).

On the other hand, from (3.12) and (3.15), It is easy to verify that (3.16) holds.

Remark 3.5. Let

()

it follows from (2.1) and (3.16) that

()

where

()

Unlike [14–16], the parameter matrices in the filtering error equation (3.19) do not contain the stochastic variable r(t), which is an interesting phenomenon. As mentioned in Definition 1 in [19], it is obvious that, if (C(t), A(t)) is detectable, then the filtering error equation (3.19) is exponentially stable. Based on the above analysis, it can be concluded that the following assumptions are necessary for the finite-time H_∞ filter design in this paper:

(i)
(C(t), A(t)) is detectable,
(ii)
w(t), v(t) ∈ ℒ₂[0, T].

4. A Numerical Example

We consider system (2.1) with the following parameters:

()

and set γ = 1.1, x(0) = [0 0]^*, p(t) = 0.8, and P₀ = I. In addition, we suppose that the noises w(t) and v(t) are generated by Gaussian with zero means and covariances Q_w = 1, Q_v = 0.02, the sampling time is 0.02 s, and the stochastic variable r(t) is simulated as in Figure 1. Based on Theorem 3.4, we design the finite-time H_∞ filter. Figure 2 shows the true value of signal z(t) and its H_∞ filtering estimate, and Figure 3 shows the estimation error

. It can be observed from the simulation results that the finite-time H_∞ filter has good tracking performance.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Stochastic variable r(t).

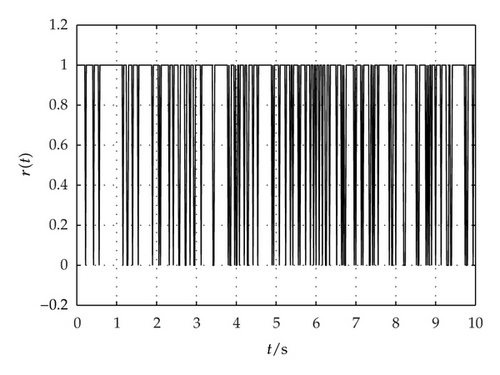
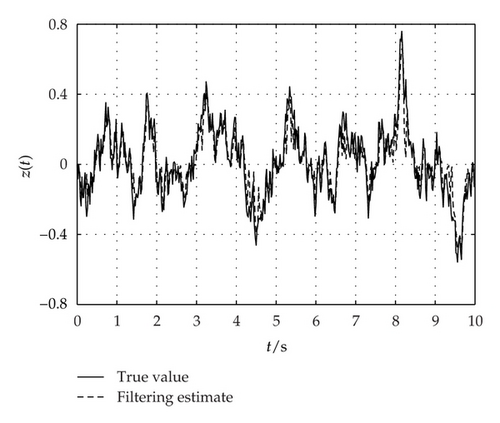
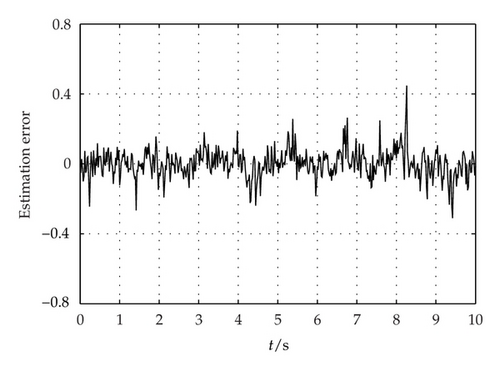
5. Conclusions

In this paper, we have proposed a new finite-time H_∞ filtering technique for linear continuous time-varying systems with uncertain observations. By introducing a Krein state-space model, it is shown that the H_∞ filtering problem can be partially equivalent to a Krein space H₂ filtering problem. A sufficient condition for the existence of the finite-time H_∞ filter is given, and the filter is derived in terms of a differential Riccati equation.

Future research work will extend the proposed method to investigate the H_∞ multistep prediction and fixed-lag smoothing problem for linear continuous time-varying systems with uncertain observations.

Acknowledgments

The authors sincerely thank the anonymous reviewers for providing valuable comments and useful suggestions aimed at improving the quality of this paper. The authors also thank the editor for the efficient and professional processing of their paper. This work is supported by the National Natural Science Foundation of China (60774004, 61034007, and 60874016) and the Independent Innovation Foundation of Shandong University, China (2010JC003).

References

1 Hassibi B., Sayed A. H., and Kailath T., Indefinite-Quadratic Estimation and Control: A Unified Approach to H2 and H∞ Theories, 1999, SIAM, New York, NY, USA, https://doi.org/10.1137/1.9781611970760, 1677962, ZBL0997.93506.
10.1137/1.9781611970760
Google Scholar
2 Kailath T., A view of three decades of linear filtering theory, IEEE Transactions on Information Theory. (1974) 20, no. 2, 146–181, 0465437, ZBL0307.93040.
10.1109/TIT.1974.1055174
Web of Science® Google Scholar
3 Zhang H. and Xie L., Control and Estimation of Systems with Input/Output Delays, 2007, 355, Springer, Berlin, Germany, 2311449.
Google Scholar
4 Anderson B. D. O. and Moore J. B., Optimal Filtering, 1979, Prentice-Hall, Englewood Cliffs, NJ, USA.
Google Scholar
5 Liu C. X., Zhang Y. Q., and Sun H. X., Finite-time H_∞ filtering for singular stochastic systems, Journal of Applied Mathematics. (2012) 2012, 16, https://doi.org/10.1155/2012/615790, 615790.
10.1155/2012/615790
Google Scholar
6 Cui J.-R., Hu G.-D., and Zhu Q., Stability and robust stability of 2D discrete stochastic systems, Discrete Dynamics in Nature and Society. (2011) 2011, 11, 545361, https://doi.org/10.1155/2011/545361, 2788365, ZBL1213.93169.
10.1155/2011/545361
Web of Science® Google Scholar
7 De la Sen M., Ibeas A., and Alonso-Quesada S., Observer-based vaccination strategy for a true mass action SEIR epidemic model with potential estimation of all the populations, Discrete Dynamics in Nature and Society. (2011) 2011, 19, 743067, https://doi.org/10.1155/2011/743067, 2846459, ZBL1233.92067.
10.1155/2011/743067
Web of Science® Google Scholar
8 De La Sen M. and Luo N., Design of linear observers for a class of linear hybrid systems, International Journal of Systems Science. (2000) 31, no. 9, 1077–1090, 2-s2.0-0034286579, https://doi.org/10.1080/002077200418351.
10.1080/002077200418351
Web of Science® Google Scholar
9 Nahi N. E., Optimal recursive estimation with uncertain observation, IEEE Transactions on Information Theory. (1969) 15, no. 4, 457–462, 0247716, ZBL0174.51102.
10.1109/TIT.1969.1054329
Web of Science® Google Scholar
10 Wang Z., Yang F., Ho D. W. C., and Liu X., Robust finite-horizon filtering for stochastic systems with missing measurements, IEEE Signal Processing Letters. (2005) 12, no. 6, 437–440, 2-s2.0-20444374021, https://doi.org/10.1109/LSP.2005.847890.
10.1109/LSP.2005.847890
CAS Web of Science® Google Scholar
11 Nakamori S., Estimation of signal using covariance information given uncertain observations in continuous-time systems, IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences. (1996) E79-A, no. 6, 736–744, 2-s2.0-0030168214.
Google Scholar
12 NaNacara W. and Yaz E. E., Recursive estimator for linear and nonlinear systems with uncertain observations, Signal Processing. (1997) 62, no. 2, 215–228, 2-s2.0-0031249546.
10.1016/S0165-1684(97)00126-6
Web of Science® Google Scholar
13 Sinopoli B., Schenato L., Franceschetti M., Poolla K., Jordan M. I., and Sastry S. S., Kalman filtering with intermittent observations, IEEE Transactions on Automatic Control. (2004) 49, no. 9, 1453–1464, https://doi.org/10.1109/TAC.2004.834121, 2086911.
10.1109/TAC.2004.834121
Web of Science® Google Scholar
14 Wang W. and Yang F. W., H_∞ filter design for discrete-time systems with missing measurements, Acta Automatica Sinica. (2006) 32, no. 1, 107–111, 2-s2.0-33645780430.
Google Scholar
15 Wang Z., Yang F., Ho D. W. C., and Liu X., Robust H_∞ filtering for stochastic time-delay systems with missing measurements, IEEE Transactions on Signal Processing. (2006) 54, no. 7, 2579–2587, 2-s2.0-33745727022, https://doi.org/10.1109/TSP.2006.874370.
10.1109/TSP.2006.874370
Web of Science® Google Scholar
16 Zhang H., Chen Q., Yan H., and Liu J., Robust H_∞ filtering for switched stochastic system with missing measurements, IEEE Transactions on Signal Processing. (2009) 57, no. 9, 3466–3474, https://doi.org/10.1109/TSP.2009.2020376, 2682700.
10.1109/TSP.2009.2020376
Web of Science® Google Scholar
17 Zhao H., Zhong M., and Zhang M., H_∞ fault detection for linear discrete time-varying systems with delayed state, IET Control Theory & Applications. (2010) 4, no. 11, 2303–2314, https://doi.org/10.1049/iet%2Dcta.2009.0215, 2798826.
10.1049/iet-cta.2009.0215
Web of Science® Google Scholar
18 Zhao H., Zhang C., Wang G., and Xing G., H_∞ estimation for a class of Lipschitz nonlinear discrete-time systems with time delay, Abstract and Applied Analysis. (2011) 2011, 22, 970978, https://doi.org/10.1155/2011/970978, 2817280, ZBL1217.93164.
10.1155/2011/970978
Google Scholar
19 Nagpal K. M. and Khargonekar P. P., Filtering and smoothing in an H_∞ setting, IEEE Transactions on Automatic Control. (1991) 36, no. 2, 152–166, https://doi.org/10.1109/9.67291, 1093089, ZBL0758.93074.
10.1109/9.67291
Web of Science® Google Scholar

Citing Literature

All articles

Finite-Time H_∞ Filtering for Linear Continuous Time-Varying Systems with Uncertain Observations

Abstract

1. Introduction

2. System Model and Problem Formulation

3. Main Results

3.1. Construct a Partially Equivalent Krein Space Problem

3.2. Solution of the Finite-Time H_∞ Filtering Problem

4. A Numerical Example

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Finite-Time H∞ Filtering for Linear Continuous Time-Varying Systems with Uncertain Observations

Abstract

1. Introduction

2. System Model and Problem Formulation

3. Main Results

3.1. Construct a Partially Equivalent Krein Space Problem

3.2. Solution of the Finite-Time H∞ Filtering Problem

4. A Numerical Example

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

Finite-Time H_∞ Filtering for Linear Continuous Time-Varying Systems with Uncertain Observations

3.2. Solution of the Finite-Time H_∞ Filtering Problem