We study the numerical solutions to semi-infinite-domain two-point boundary value problems and initial value problems. A smooth, strictly monotonic transformation is used to map the semi-infinite domain x ∈ [0, ∞) onto a half-open interval t ∈ [−1, 1). The resulting finite-domain two-point boundary value problem is transcribed to a system of algebraic equations using Chebyshev-Gauss (CG) collocation, while the resulting initial value problem over a finite domain is transcribed to a system of algebraic equations using Chebyshev-Gauss-Radau (CGR) collocation. In numerical experiments, the tuning of the map ϕ : [−1, +1)→[0, +∞) and its effects on the quality of the discrete approximation are analyzed.

1. Introduction

Boundary value problems (BVPs) on infinite intervals and initial value problems (IVPs) frequently occur in mathematical modelling of various applied problems. Typically, these problems arise very frequently in fluid dynamics, aerodynamics, quantum mechanics, electronics, astrophysics, and other domains of science, as examples, in the study of unsteady flow of a gas through a semi-infinite medium [1–3], heat transfer in the radial flow between parallel circular disks [4], draining flows [5], circular membranes [6–8], plasma physics [9, 10], radially symmetric solutions of semilinear elliptic equations [10–12], non-Newtonian fluid flows [13], study of stellar structure, thermal behavior of a spherical cloud of gas, isothermal gas sphere, theory of thermionic currents [14–16], and modeling of vortex solitons [17, 18].

The analytical solutions to BVPs and IVPs are not readily attainable and thus the need for finding efficient computational algorithms for obtaining numerical solutions arises. During the last few years much progress has been made in the numerical treatment of boundary value problems over infinite intervals (see e.g., [19–23] and references therein). Moreover, different spectral methods have been proposed for solving problems on unbounded domains. One of the methods is through the use of polynomials that are orthogonal over unbounded domains, such as the Hermite spectral and the Laguerre spectral methods [24–29]. However, all of these algorithms need certain quadratures on unbounded domains, which introduce errors and so weaken the merit of spectral approximations.

Another approach is replacing the infinite domain with [−L, L] and the semi-infinite interval with [0, L] by choosing L sufficiently large. This method is named as the domain truncation [30]. When we use finite difference methods or finite element methods to solve unbounded problems numerically, we often utilize domain truncation and impose certain conditions on artificial boundaries, which destroy the accuracy usually [22].

Another direct approach for solving such problems is based on rational approximations. Christov [31] and Boyd [32, 33] developed some spectral methods on unbounded intervals by using mutually orthogonal systems of rational functions. Boyd [33] defined a new spectral basis, named rational Chebyshev functions on the semi-infinite interval, by mapping it to the Chebyshev polynomials. Guo et al. [34] introduced a new set of rational Legendre functions that are mutually orthogonal in L²(0, +∞). They applied a spectral scheme using the rational Legendre functions for solving the Korteweg-de Vries equation on the half-line. Boyd et al. [35] applied pseudospectral methods on a semi-infinite interval and compared the rational Chebyshev, the Laguerre and the mapped Fourier sine methods. The authors of [36–40] solved some IVPs and BVPs on semi-infinite intervals.

The use of a suitable mapping to transfer infinite domains to the finite domains and then applying the standard spectral methods for the transformed problems in finite domains is another approach that is frequently used [41–45] and is used in this paper too.

In this paper we describe two collocation methods for the numerical solution of semi-infinite-domain two-point boundary value problems and initial value problems. For mapping the semi-infinite domain x ∈ [0, ∞) onto a finite half-open interval t ∈ [−1, +1), the algebraic and logarithmic transformations, which are smooth and strictly monotonic, are used. The Chebyshev-Gauss (CG), Chebyshev-Gauss-Radau (CGR), and Chebyshev-Gauss-Lobatto (CGL) points are then introduced. Then, the resulting finite-domain two-point boundary value problem is discretized using CG collocation, and the resulting initial value problem over a finite domain is discretized using CGR collocation in order to handle the initial slope condition based on the collocation points. Our collocation schemes avoid the singularity at t = +1 introduced by the change of variables because the final CG or CGR point is strictly smaller than t = +1. Furthermore, in the CG scheme for two-point boundary value problems, the function at x = +∞ is obtained directly from the final condition, while, in the CGR scheme for initial value problems, the function at x = +∞ is estimated after solving the problem. In addition, we find that if the exact solution to the original problem decays exponentially fast as x → ∞, then better approximations to the problem can be attained by using a transformation x = ϕ(t) that grows more slowly near the point t = +1, while if the exact solution decays algebraically as x → ∞, then better approximations to the problem can be attained by using a transformation that grows more rapidly near the point t = +1. Thus, by tuning the choice of the transformation, the accuracy of the discretization can be improved.

This paper is organized as follows: in Section 2, using algebraic and logarithmic transformations we transform the semi-infinite-domain BVPs and IVPs to finite-domain problems. In Section 3, we discuss the choices for collocation points and explain our method. Section 4 is devoted to some numerical examples and analysis of tuning the transformations. Finally, in Section 5 we provide conclusions.

2. Problem Statement and Domain Transformation

Consider the semi-infinite-domain two-point boundary value problem as

()

where f is a continuous function and c₀ and c₁ are known constants. Also, consider the initial value problem over a semi-infinite domain as defined by (2.1) with the conditions

()

where c₀ and

are known constants and in this case we assume that lim _x→∞ y(x) exists.

We make the change of variables x = ϕ(t), where ϕ is a differentiable, strictly monotonic function of t that maps the interval [−1,1) onto [0, ∞). There are several typical mappings that relate infinite and finite domains to each other, but three specific types of mappings, as algebraic, logarithmic, and exponential, are more practical. Typical examples of such functions are the algebraic transformation

()

and the logarithmic transformation

()

where L is a positive parameter that is called mapping parameter, and in this paper we set K = 1/2, 1, and 3/2. Note that other positive values for K are possible, but these values seem to be proper for a wide range of problems. Algebraic transformation with K = 1 and exponential transformation were proposed in [41, 42], while other algebraic transformations are introduced in this paper.

Boyd in [30, 42] offered guidelines for optimizing the mapping parameter L where L > 0. Boyd used these guidelines to obtain approximations to known functions and not to find solutions to differential equations. In general, there is no way to avoid a small amount of trial and error in choosing L when solving problems on an infinite domain. Note that the optimum value of L varies with the number of collocation points, and, as Boyd [30] stated, for smooth functions the error is relatively insensitive to the precise choice of L in the neighborhood of the optimum value of L.

As we will see in the numerical experiments, better discretization can be achieved by tuning the transformations to the problem. For a fixed L, the logarithmic transformation produces slower growth in x = ϕ(t) as t approaches +1 than that of algebraic transformations introduced here. Moreover, in algebraic transformations by increasing K faster growth in x = ϕ(t) is produced. However, the logarithmic transformation and the algebraic transformation with K = 1/2 have almost the same behavior. In particular, we will see that if the exact solution to the original problem decays exponentially fast as x → ∞, then both transformations (algebraic and logarithmic) work, but logarithmic transformation and algebraic transformation with K = 1/2 give better results in comparison with other choices for algebraic transformations. On the other hand, if the exact solution decays algebraically as x → ∞, then algebraic transformations with K = 1 and K = 3/2 give much better results. Furthermore, the smoothness of the exact solution in the transformed coordinate plays an important role in tuning the transformations to the problem.

The transformations in (2.4)-(2.5) are especially convenient because they yield simple expressions for derivatives. With a general transformation x = ϕ(t) with ϕ^′(t) > 0, −1 ⩽ t ⩽ 1, the first and second derivatives of y(x) can be expressed in terms of t as follows:

()

After changing variables from x to t, the nonlinear differential equation in (2.1) becomes

()

Moreover, the boundary conditions in (2.2) become

()

while the initial conditions in (2.3) become

()

3. Collocation Methods for Semi-Infinite-Domain BVPs and IVPs

In this section we formulate discrete approximations to the problems described in Section 2. These schemes are based on global collocation using CG and CGR collocation points. As will be seen, the schemes for semi-infinite-domain two-point boundary value problems and for initial value problems are different in respect of their treatment of the origin and the infinity. For semi-infinite-domain two-point boundary value problems, the function value at the infinity is obtained directly from the boundary condition at the infinity, while for initial value problems the derivative at the origin is expanded based on collocation points to handle the initial slope condition, and the function value at the infinity is estimated after obtaining the approximate solution.

3.1. CG, CGR, and CGL Collocation Points

The CG, CGR, and CGL collocation points [46] lie on the open interval (−1,1), the half-open interval [−1,1) or (−1,1], and the closed interval [−1,1], respectively. The CG points contain neither −1 nor 1, the CGR points contain only one of the points −1 or 1, and the CGL points contain both −1 and 1. The CG points are the roots of T_N(t) (Nth-degree Chebyshev polynomial) as

()

the CGR points are defined by

()

and the CGL points are the roots of

()

It is known that the CG and CGL points are symmetric about the origin whereas the CGR points are asymmetric. In addition, the CGR points are not unique in that two sets of points exist (one including the point −1 and the other including the point +1). The CGR points that include the initial point are called the standard CGR points and the CGR points that include the terminal end point are often called the flipped CGR points.

3.2. Gauss Collocation Scheme for Infinite-Domain Two-Point Boundary Value Problems

Consider a set of CG collocation points (t₁, t₂, …, t_N) defined by (3.1) on the interval (−1,1) and two additional noncollocated points t₀ = −1 and t_N+1 = 1 (the terminal value, corresponding to x = +∞). The function Y ∈ L²[−1,1] is approximated by a polynomial of degree at most N + 1 as

()

where Y_j = Y(t_j) and

()

is a basis of (N + 1)th-degree Lagrange polynomials satisfying L_j(t_i) = δ_ij. Notice that the basis includes the functions L₀ and L_N+1 corresponding to the initial value t₀ = −1 (x = 0) and the terminal value t_N+1 = 1 (x = +∞).

The derivative matrix

at CG collocation points t_i, i = 1,2, …, N is defined by

()

and the second derivative

is defined by

()

For computing the entries of D⁽¹⁾ and D⁽²⁾, we follow the method proposed in [47]. According to [47] the entries of D⁽¹⁾ are computed by

()

where i = 1,2, …, N, j = 0,1, …, N + 1, and

. For large value of N, the computation of ratio c_i/c_j in

may cause round-off error, and therefore to avoid this problem as mentioned in [47] we can compute them as

()

The entries of matrix D⁽²⁾ can be computed recursively by the entries of D⁽¹⁾ as follows:

()

Similarly, higher-order derivative matrices can be computed recursively by lower-order ones. For more details, see [47].

Therefore, the approximations of the first and second derivatives of the series of (3.4) at CG collocation points t_i, i = 1,2, …, N, are obtained as follows:

()

where

and

are the ith row of D⁽¹⁾ and D⁽²⁾, respectively. The rectangular N × (N + 2) matrices D⁽¹⁾ and D⁽²⁾ formed by the coefficients

and

, (i = 1, …, N, j = 0, …, N + 1) are the first- and second-order Gauss differentiation matrices since they transform the approximation of Y(t) at t₀, …, t_N+1 to the first and second derivatives of Y(t) at the gauss collocation points t₁, …, t_N.

Our discrete approximation to the semi-infinite-domain two-point boundary value problem in (2.1)-(2.2) is obtained as follows. After transformation of the domain, approximating the function Y using the series of (3.4) and evaluating the boundary conditions in (2.8) at noncollocated (but interpolation) points t₀ = −1 and t_N+1 = 1 imply

()

As a result, N unknowns Y₁, …, Y_N remain to be determined. By evaluating (2.7) at each collocation point t_i, i = 1, …, N, and replacing Y^′(t_i) and Y^′′(t_i) by their discrete approximations in (3.11)-(3.12) we obtain

()

By using (3.14) we generate a set of N nonlinear algebraic equations for the unknowns Y₁, …, Y_N that can be solved using Newton’s iterative method. It is well known that the initial guess for Newton’s iterative method is important especially for complicated problems. To choose the initial guess for our problem, in the first stage we set N = 5 and apply Newton’s iterative method for solving N nonlinear equations by choosing the values of the linear function between the boundary conditions in (2.8) as our initial guesses. We then increase N by 5 or 10 and use the approximate solution at stage one as our initial guess for the next stage. We continue this approach until the results are similar up to a required number of decimal places for two consecutive stages.

Note that, although the transformed two-point boundary value problem in (2.7) may have a singularity at t = −1 and the change of variable x = ϕ(t) must have a singularity at t = +1, we never evaluate the problem at the singularities, rather we evaluate it at the collocation points that are all strictly more than −1 and less than 1.

With substituting the obtained values of Y_j, j = 0,1, …, N + 1, in (3.4) the approximation of Y(t) is obtained. Finally, the approximate solutions on [0, ∞) using the algebraic transformations in (2.4) with K = 1/2, 1, and 3/2 are found as

()

respectively, where

()

and the approximate solution on [0, ∞) using the logarithmic transformation in (2.5) is found as

()

3.3. Radau Collocation Scheme for Initial Value Problems

Consider the standard CGR collocation points −1 = t₀ < ⋯<t_N < +1 defined by (3.2) and the additional noncollocated point t_N+1 = 1. As the CG scheme, the function Y is approximated using (3.4). It is worth mentioning that for the Radau scheme, the point t₀ is a collocation point, while, for the Gauss scheme in the previous subsection, the point t₀ is just an interpolation node. For IVPs, the CGR points are more appropriate because they allow approximation of the initial slope condition to be obtained based on collocation points.

Again, the derivative matrix D⁽¹⁾ at CGR collocation points t_i, i = 0,1, …, N, is defined by

()

and the second derivative D⁽²⁾ is defined by

()

The elements of D⁽¹⁾ and D⁽²⁾ are computed similarly to the previous subsection with the difference that here i = 0,1, …, N. In addition, the approximations of the first and second derivatives of the series of (3.4) at CGR collocation points t_i, i = 0,1, …, N, are obtained using (3.11)-(3.12). Notice that, in the CGR scheme, unlike the CG scheme, the approximation of Y^′(t₀) is obtained based on collocation points. The rectangular (N + 1)×(N + 2) matrices D⁽¹⁾ and D⁽²⁾ formed by the coefficients

and

, (i = 0, …, N, j = 0, …, N + 1) are the first- and second-order Radau differentiation matrices, respectively. These matrices transform the approximation of Y(t) at t₀, …, t_N+1 to the first and second derivatives of Y(t) at the Radau collocation points t₀, …, t_N.

The discrete approximation to the initial value problem in (2.1) and (2.3) is obtained as follows. After transformation of the domain, by approximating the function Y using the series of (3.4) and evaluating the boundary conditions in (2.9) at the collocation (also interpolation) point t₀ = −1 and using (3.11) we obtain

()

Consequently, N + 1 unknowns Y₁, Y₂, …, Y_N+1 remain to be determined. Unlike the CG scheme for infinite-domain BVPs, in the CGR scheme for IVPs the function value at the infinity, Y_N+1, appears in the unknowns. As the CG scheme, we evaluate (2.7) at collocation points t_i for i = 1, …, N and replace Y^′(t_i) and Y^′′(t_i) by their discrete approximations in (3.11)-(3.12) to generate N algebraic equations, by which in combination with (3.21) we obtain a set of N + 1 algebraic equations for the unknowns Y₁, Y₂, …, Y_N+1. In this case, to choose the initial guess for Newton’s iterative method, in the first stage we set N = 5 and apply Newton’s iterative method for solving N + 1 nonlinear equations by choosing c₀ in (2.9) as our initial guess. We then proceed the procedure described for the CG scheme.

Note that the CGR scheme of this subsection can also be applied for infinite-domain two-point boundary values problems in Section 3.2. Nevertheless, the errors using either the CG or CGR schemes are almost the same.

3.4. Assessment of Spectral Accuracy

The convergence properties of the approximation to y(x) can be determined from the behavior of the function Y(t) = y(ϕ(t)). Infinite-order accuracy is expected when Y(t) is infinitely smooth on [−1,1]. Assuming that y(x) itself is infinitely smooth on [0, +∞), the critical issue is the behavior of the derivatives of Y(t) at t = 1. Moreover, unlike expansions on a finite domain, spectral approximations on a semi-infinite domain have two discretization parameters, the mapping parameter L in addition to the number of collocation points. Furthermore, the decay rate of the solution y(x) plays an important role in investigating the convergence properties. More precisely, if y(x) decays exponentially fast as x → ∞, then better approximations to the problem can be attained by using a transformation x = ϕ(t) that grows more slowly near the point t = +1, while if y(x) decays algebraically as x → ∞, then better approximations can be attained by using a transformation that grows more rapidly near the point t = +1. In the next section, we analyze the effects of the mentioned parameters via test examples.

4. Illustrative Examples

We tested the methods presented in this paper on several problems such as the problem of unsteady flow of gas through a semi-infinite porous medium and the Flierl-Petviashvili (FP) equation. For the FP equation, a modified version of the Radau scheme of this paper is introduced in order to approximate the FP monopole. In this section we also analyze tuning the transformations to the problems. All solutions were obtained using the well-known symbolic software “Mathematica 8."

4.1. Semi-Infinite-Domain Two-Point Boundary Value Problems

Example 4.1. We begin with a simple example to illustrate and analyze tuning the transformations. Consider the linear semi-infinite-domain two-point boundary value problem [22]

()

The exact analytical solution is

. The problem in (4.1) was solved for N = (10, 20, 30) using the collocation method described in Section 3.2 with the CG collocation points described in Section 3.1 and with the strictly monotonic transformations of the domain t ∈ [−1,1) given in (2.4)-(2.5).

The maximum absolute error is defined by

()

where I_N+1(Y)(t) and Y_e(t) are the approximated and exact solutions in the transformed coordinate, respectively. The maximum absolute errors obtained using the CG scheme of this paper, are given in Table 1 with the logarithmic transformation and the algebraic transformations with K = 1/2, 1, and 3/2 given in (2.4)-(2.5). As can be seen, for all four transformations, the errors decrease until N = 30, demonstrating an approximately exponential convergence rate. It is seen that, for each value of N, there exists an optimal value for the mapping parameter L and this optimal value varies with the transformation. In addition, it is observed that changing the values of mapping parameter L improves the quality of the discretization, significantly. For example, for N = 20, the maximum absolute error using the logarithmic transformation ϕ_l decreases from 2.72 × 10⁻⁸ for L = 1 to 1.80 × 10⁻¹⁵ for L = 5. Moreover, the logarithmic transformation ϕ_l allows accurate results to be obtained much more efficiently. For example, to achieve an error of less than 10⁻¹⁴ we require less than 20 collocation points using the logarithmic transformation with L = 3, while for other transformations more collocation points are needed (see Table 1). However, the algebraic transformation ϕ_a with K = 1/2 produces very satisfactory results too. Finally, it is seen that for each value of N, the best maximum absolute error for logarithmic transformation is less than that for algebraic transformations.

The different behavior of the transformations given in (2.4)-(2.5) is understood if we apply the change of variables to the continuous solution. The exact solution in the transformed coordinates is as follows:

()

Here the subscripts a and l correspond to the algebraic and logarithmic transformations given in (2.4)-(2.5). An advantage of using the logarithmic change of variable and also the algebraic change of variable with K = 1/2, as compared to other algebraic change of variables, is that for proper values of L they essentially move collocation points associated with large values of x to the left. Because the exact solution changes slowly when x is large, this leftward movement of the collocation points is beneficial since more collocation points are situated where the solution is changing most rapidly. The disadvantage of a logarithmic change of variables is seen in the function ln (1 − t) where the growth is so slow near t = +1 that the transformed solution possesses a singularity in a derivative at t = +1. In other words, the jth derivative of a function of the form (1 − t) ^α, where α > 0 is not an integer, is singular at t = +1 for j > α. To achieve exponential convergence, Y(t) should be infinitely smooth. For this particular problem, it is seen that for K = 1/2,1, and 3/2, Y_a(t) and all its derivatives with respect to t approach 0 as t → 1⁻, thus, algebraic transformations ϕ_a(t) would produce satisfactory results (see Table 1). On the other hand, Y_l(t) is relatively smooth with

derivatives at t = +1 if L is an integer and with [2L] derivatives if L is not an integer ([·] denotes the greatest integer value), although not infinitely smooth, and with a proper value for L, collocation points corresponding to large values of x, where the solution changes slowly, are moved to the left (when compared to the algebraic transformations) where the solution changes more rapidly. As a result, for 10 ⩽ N ⩽ 30, the logarithmic transformation yields a solution that is often more accurate than the other choices for ϕ.

The problem in (4.1) has been solved in [22] using domain truncation and a forth-order finite difference method (FFDM) and later in [23] using the precise time integration (PTI) method. In Table 2, a comparison is made between the values obtained using the present CG collocation method with the logarithmic transformation ϕ_l for L = 5 and N = 20, method in [22] with truncated domain [0,10] and h = 1/64, and method in [23] with matrix exponential technique. It is seen that our method is more accurate than the FFDM and PTI methods, and even though the exact results become extremely small when x > 6, our method is still capable of giving results with high precision.

Table 1. Maximum absolute errors for Example 4.1.

Mapping	N	L
Mapping	N	1	2	3	4	5	6
ϕ_a(t) K = 1/2	10	3.31 × 10⁻⁶	2.22 × 10⁻⁷	5.96 × 10⁻⁷	4.65 × 10⁻⁵	4.22 × 10⁻⁴	2.08 × 10⁻³
	20	8.48 × 10⁻⁸	3.42 × 10⁻¹⁰	9.20 × 10⁻¹²	2.95 × 10⁻¹³	1.16 × 10⁻¹³	4.12 × 10⁻¹¹
	30	3.10 × 10⁻⁹	9.60 × 10⁻¹³	8.51 × 10⁻¹⁵	8.40 × 10⁻¹⁵	8.00 × 10⁻¹⁵	8.00 × 10⁻¹⁵
ϕ_a(t) K = 1	10	1.32 × 10⁻⁴	1.14 × 10⁻⁵	4.05 × 10⁻⁶	4.46 × 10⁻⁶	2.32 × 10⁻⁵	5.81 × 10⁻⁵
	20	4.18 × 10⁻⁷	4.00 × 10⁻⁸	1.34 × 10⁻⁸	7.20 × 10⁻⁹	6.43 × 10⁻⁹	4.77 × 10⁻⁹
	30	6.58 × 10⁻⁹	1.71 × 10⁻¹⁰	1.45 × 10⁻¹¹	1.05 × 10⁻¹¹	2.53 × 10⁻¹²	9.52 × 10⁻¹³
ϕ_a(t) K = 3/2	10	5.75 × 10⁻⁴	2.78 × 10⁻⁴	2.21 × 10⁻⁴	3.20 × 10⁻⁴	2.38 × 10⁻⁴	1.75 × 10⁻⁴
	20	5.47 × 10⁻⁶	8.18 × 10⁻⁷	3.55 × 10⁻⁷	6.47 × 10⁻⁸	9.80 × 10⁻⁸	4.63 × 10⁻⁸
	30	5.42 × 10⁻⁸	6.15 × 10⁻⁹	2.10 × 10⁻⁹	1.29 × 10⁻⁹	7.22 × 10⁻¹⁰	1.88 × 10⁻¹⁰
ϕ_l(t)	10	1.06 × 10⁻⁶	5.41 × 10⁻⁹	6.18 × 10⁻¹⁰	2.83 × 10⁻⁹	5.55 × 10⁻⁶	8.42 × 10⁻⁵
	20	2.72 × 10⁻⁸	3.11 × 10⁻¹²	4.25 × 10⁻¹⁵	2.95 × 10⁻¹⁵	1.80 × 10⁻¹⁵	6.10 × 10⁻¹⁵
	30	3.12 × 10⁻⁹	4.61 × 10⁻¹⁴	3.52 × 10⁻¹⁵	1.65 × 10⁻¹⁵	1.05 × 10⁻¹⁵	5.07 × 10⁻¹⁵

Table 2. Approximate and exact values of y(x) for Example 4.1.

x	FFDM [22]	PTI [23]	Present method	Exact
1	1.00220 × 10⁻¹	1.0021048 × 10⁻¹	1.002104788741 × 10⁻¹	1.002104788741 × 10⁻¹
2	1.12776 × 10⁻²	1.1275892 × 10⁻²	1.127589195768 × 10⁻²	1.127589195768 × 10⁻²
4	1.76737 × 10⁻⁴	1.7670378 × 10⁻⁴	1.767037762946 × 10⁻⁴	1.767037762946 × 10⁻⁴
6	3.11068 × 10⁻⁶	3.1101148 × 10⁻⁶	3.110114828388 × 10⁻⁶	3.110114828396 × 10⁻⁶
8	5.63886 × 10⁻⁸	5.6428565 × 10⁻⁸	5.642859756603 × 10⁻⁸	5.642859752063 × 10⁻⁸
10	8.13692 × 10⁻¹⁰	—	1.031258865734 × 10⁻⁹	1.031258873612 × 10⁻⁹
12	—	—	1.887856605151 × 10⁻¹¹	1.887856203661 × 10⁻¹¹
14	—	—	3.457320525861 × 10⁻¹³	3.457322449053 × 10⁻¹³
15	—	—	4.679133135965 × 10⁻¹⁴	4.678891146411 × 10⁻¹⁴

Example 4.2. Consider the following nonlinear semi-infinite-domain two-point boundary value problem:

()

The exact analytical solution is

. This example was solved for N = (10, 20, 30, 40) using the CG collocation method described in Section 3.2 with the strictly monotonic transformations of the domain t ∈ [−1,1) given in (2.4)-(2.5).

The maximum absolute errors obtained using the CG scheme of this paper are given in Table 3. In this example, the exact solution decays algebraically; thus, algebraic transformations yield more accurate results in comparison with the logarithmic transformation. It is seen from Table 3 that for this problem the algebraic transformations are relatively not sensitive to the mapping parameter L. In addition, the algebraic transformation ϕ_a with K = 3/2 allows accurate results to be obtained more efficiently, and as N increases the errors obtained using this transformation decay more rapidly than the errors obtained using other choices for ϕ. For example, for N = 40, using ϕ_a with K = 1 and L = 5 the maximum absolute error is obtained as 2.18 × 10⁻⁷, while using ϕ_a with K = 3/2 and L = 5 the maximum absolute error is obtained as 1.05 × 10⁻⁹ (see Table 3). An advantage of using the algebraic change of variable ϕ_a with K = 3/2, as compared to other changes of variables, is that it moves collocation points to the right. Because the exact solution decays slowly, this rightward movement of the collocation points is beneficial since more collocation points are situated where x is large.

Now, consider the exact continuous solution in the transformed coordinates using the transformations given in (2.4)-(2.5) as

()

The subscripts a and l correspond to the algebraic and logarithmic transformations. The second reason that the transformation ϕ_a with K = 3/2 yields more accurate results is related to the smoothness of Y_a(t) and Y_l(t). It can be easily seen that Y_a(t) with K = 3/2 has two derivatives as t → 1⁻, while Y_a(t) with K = 1 has one derivative. In addition, the first derivatives of functions Y_a(t) with K = 1/2 and Y_l(t) approach −∞ as t → 1⁻, which induces a relatively large error when these transformations are used.

Table 3. Maximum absolute errors for Example 4.2.

Mapping	N	L
Mapping	N	1	2	3	4	5	6
ϕ_a(t) K = 1/2	10	5.84 × 10⁻³	2.23 × 10⁻³	1.31 × 10⁻²	1.79 × 10⁻²	3.62 × 10⁻²	7.23 × 10⁻²
	20	1.77 × 10⁻³	6.45 × 10⁻⁴	3.56 × 10⁻⁴	3.62 × 10⁻⁴	2.00 × 10⁻⁴	1.36 × 10⁻³
	30	7.63 × 10⁻⁴	2.40 × 10⁻⁴	1.39 × 10⁻⁴	9.40 × 10⁻⁵	6.12 × 10⁻⁵	4.95 × 10⁻⁵
	40	4.10 × 10⁻⁴	1.38 × 10⁻⁴	7.75 × 10⁻⁵	5.53 × 10⁻⁵	3.60 × 10⁻⁵	2.74 × 10⁻⁵
ϕ_a(t) K = 1	10	1.85 × 10⁻³	2.71 × 10⁻³	5.81 × 10⁻³	1.22 × 10⁻²	4.83 × 10⁻²	2.28 × 10⁻²
	20	2.62 × 10⁻⁵	1.47 × 10⁻⁵	3.45 × 10⁻⁵	9.53 × 10⁻⁵	1.23 × 10⁻⁴	3.61 × 10⁻⁴
	30	7.20 × 10⁻⁶	2.45 × 10⁻⁶	1.31 × 10⁻⁶	1.00 × 10⁻⁶	2.89 × 10⁻⁶	6.57 × 10⁻⁶
	40	2.84 × 10⁻⁶	1.00 × 10⁻⁶	5.55 × 10⁻⁷	3.40 × 10⁻⁷	2.18 × 10⁻⁷	2.60 × 10⁻⁷
ϕ_a(t) K = 3/2	10	7.24 × 10⁻³	7.19 × 10⁻³	1.48 × 10⁻²	1.12 × 10⁻²	1.92 × 10⁻²	6.81 × 10⁻²
	20	6.95 × 10⁻⁵	5.47 × 10⁻⁵	5.75 × 10⁻⁵	1.07 × 10⁻⁴	1.81 × 10⁻⁴	2.24 × 10⁻⁴
	30	7.52 × 10⁻⁷	5.63 × 10⁻⁷	8.65 × 10⁻⁷	1.57 × 10⁻⁶	2.98 × 10⁻⁶	3.82 × 10⁻⁶
	40	1.12 × 10⁻⁸	3.64 × 10⁻⁹	1.94 × 10⁻⁹	1.22 × 10⁻⁹	1.05 × 10⁻⁹	1.14 × 10⁻⁹
		L
		1	5	10	15	20	25
ϕ_l(t)	10	6.78 × 10⁻²	2.31 × 10⁻²	7.22 × 10⁻²	3.75 × 10⁻¹	—	—
	20	6.40 × 10⁻²	1.11 × 10⁻²	3.85 × 10⁻³	5.58 × 10⁻³	1.77 × 10⁻²	1.22 × 10⁻²
	30	7.20 × 10⁻²	8.00 × 10⁻³	2.95 × 10⁻³	1.65 × 10⁻³	9.96 × 10⁻⁴	1.56 × 10⁻³
	40	3.82 × 10⁻²	7.15 × 10⁻³	2.55 × 10⁻³	1.43 × 10⁻³	9.00 × 10⁻⁴	6.95 × 10⁻⁴

Example 4.3. In this example we consider the nonlinear semi-infinite-domain two-point boundary value problem due to Kidder [2] as

()

which appears in the problem of the transient flow of gas [2] within a one-dimensional semi-infinite porous medium. The typical boundary conditions imposed by the physical properties are

()

The problem in (4.6)-(4.7) was handled by Kidder [2] where a perturbation technique is carried out to include terms of the second order. The principal limitation of his work is that the complexity of the calculations increases rapidly with increasing order of the terms. Moreover, Countryman and Kannan [48], without solving the problem in (4.6)-(4.7), showed that the lower and upper solutions β(x) and γ(x) for this problem are obtained from the linear infinite-domain two-point boundary value problems

()

respectively. It can be easily seen that the solutions β(x) and γ(x) are given by

()

where the error function is defined by

()

Further,

()

where y(x) is the solution to (4.6)-(4.7).

In this example the solution decays exponentially fast as x increases; thus, according to the results obtained in Examples 4.1 and 4.2, we solve this problem using the logarithmic transformation ϕ_l and also using the algebraic transformation ϕ_a with K = 1/2. It is worth mentioning that for problems whose exact solution is not available, we first solve the problem using the algebraic transformation ϕ_a with K = 1 and N = 30 to determine the decay rate of the solution. We then tune the transformations, appropriately, to improve the quality of our discretization technique.

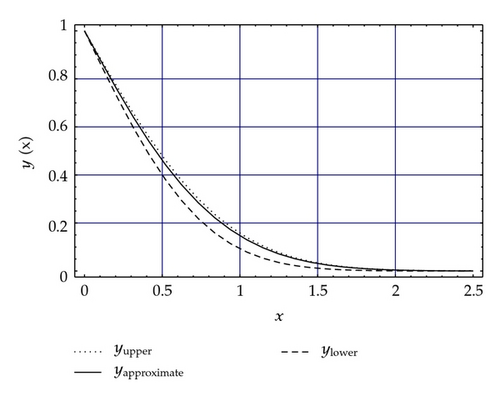
For comparison purposes, the estimated values of y(x) for specific value of α = 0.5 obtained using the perturbation method in [2], the CG scheme of this paper with ϕ_l for L = 4 and N = 50 together with the lower and upper solutions [48] given in (4.9), are listed in Table 4. In addition, in Table 5 we give the approximate values of y(x) obtained using the present CG method for α = 0.5 and different transformations. It is seen that both transformations ϕ_a with K = 1/2 and ϕ_l produce almost the same results. Moreover, the values obtained using the present method highly agree with the upper solutions given in Table 4, while the value of y(x) obtained by the perturbation method [2] deviates from the upper solution at x = 1. In addition, as expected, changing the values of the mapping parameter L improves the precision of our collocation method. For example, at x = 5 the value of y(x) obtained using both transformations for L = 1, a bit deviate from the upper solution given in Table 4, while increasing L to L = 4, improves the precision (see Table 5). The computational results for y(x) using the present CG scheme with ϕ_l, L = 4, and N = 50 together with the lower and upper solutions in (4.9) are shown in Figure 1. Finally, we note that unlike the perturbation technique used by Kidder [2], where the complexity of the calculations increases rapidly with the increase of order of terms, the present CG scheme leads to approximation through a reduced size of calculations.

Table 4. Approximate, lower, and upper values of y(x) for Example 4.3.

x	Kidder [2]	Lower solution [48]	Upper solution [48]	Present method
0.1	0.8816588283	0.8664422385	0.8875370840	0.881364651392
0.2	0.7663076781	0.7366004905	0.7772974108	0.765828813075
0.3	0.6565379995	0.6138834718	0.6713732405	0.656000684962
0.4	0.5544024032	0.5011272661	0.5716076449	0.553898941764
0.5	0.4613650295	0.4004059668	0.4795001222	0.460942762761
0.6	0.3783109315	0.3129383317	0.3961439092	0.377981584588
0.7	0.3055976546	0.2390937496	0.3221988062	0.305352338492
0.8	0.2431325473	0.1784850363	0.2578990353	0.242954391586
0.9	0.1904623681	0.1301238831	0.2030917876	0.190334233477
1.0	0.1587689826	0.0926090195	0.1572992071	0.146773312549
2.0	—	0.0007693696	0.0046777350	0.004299182851
3.0	—	4.5262 × 10⁻⁷	0.0000220905	0.000020292763
4.0	—	1.730 × 10⁻¹¹	1.5417 × 10⁻⁸	1.416256 × 10⁻⁸
5.0	—	1.388 × 10⁻¹⁷	1.537 × 10⁻¹²	1.41205 × 10⁻¹²

Table 5. Approximate values of y(x) for Example 4.3 obtained using the present method with N = 50.

x	ϕ_a (K = 1/2)		ϕ_l
x	L = 1	L = 4	L = 1	L = 4
0.1	0.881364651392	0.881364651392	0.881364651393	0.881364651392
0.2	0.765828813074	0.765828813075	0.765828813076	0.765828813075
0.3	0.656000684962	0.656000684962	0.656000684960	0.656000684962
0.4	0.553898941764	0.553898941764	0.553898941764	0.553898941764
0.5	0.460942762760	0.460942762761	0.460942762762	0.460942762761
0.6	0.377981584586	0.377981584588	0.377981584588	0.377981584588
0.7	0.305352338493	0.305352338492	0.305352338489	0.305352338492
0.8	0.242954391588	0.242954391586	0.242954391585	0.242954391586
0.9	0.190334233474	0.190334233477	0.190334233480	0.190334233477
1.0	0.146773312552	0.146773312549	0.146773312546	0.146773312549
2.0	0.004299182854	0.004299182851	0.004299182856	0.004299182851
3.0	0.000020292768	0.000020292763	0.000020292759	0.000020292763
4.0	1.415843 × 10⁻⁸	1.416261 × 10⁻⁸	1.416474 × 10⁻⁸	1.416256 × 10⁻⁸
5.0	2.30431 × 10⁻¹²	1.40494 × 10⁻¹²	1.68339 × 10⁻¹²	1.41205 × 10⁻¹²

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Computational results of y(x), lower and upper solutions for Example 4.3.

4.2. Initial Value Problems

Example 4.4. Consider the Lane-Emden equation given by

()

where lim _x→∞ y(x) = 0. The exact analytical solution is given in [50] by

. The problem in (4.12) was solved for N = (20, 30, 40) using the CGR collocation scheme described in Section 3.3 with the strictly monotonic algebraic transformations of the domain t ∈ [−1,1) given in (2.4). As stated in Section 3, in the CGR scheme of this paper, the function value at t = +1 (x = +∞) is an unknown variable in the discretization and is approximated after obtaining the approximate solution. The maximum absolute errors together with the approximate values of y(∞) obtained using the CGR scheme of this paper and the algebraic transformations ϕ_a with K = 1/2, 1, and 3/2 are given in Table 6.

Similarly to Example 4.2, the exact solution of this problem decays algebraically, and, hence, algebraic transformations allow accurate results to be obtained more efficiently and they are relatively not sensitive to the mapping parameter L. But, unlike Example 4.2, here, ϕ_a with K = 1 is more accurate than ϕ_a with K = 3/2. Again, the different behavior of these transformations is understood by considering the exact solution in the transformed coordinates using the algebraic transformations as

()

It can be easily seen that Y_a(t) with K = 1 is infinitely smooth, while Y_a(t) with K = 3/2 has just one derivative as t → 1⁻ and also

with K = 1/2 approaches −∞ as t → 1⁻. As a result, for this particular problem, the algebraic transformation with K = 1 yields a solution that is by far more accurate than other choices for ϕ.

Table 6. Maximum absolute errors and approximations of y(∞) for Example 4.4.

Mapping	N	L				(L, y(∞))
Mapping	N	1	2	3	4	(L, y(∞))
ϕ_a(t) K = 1/2	20	1.87 × 10⁻²	9.32 × 10⁻³	6.21 × 10⁻³	4.65 × 10⁻³	(4,4.6534 × 10⁻³)
	30	1.26 × 10⁻²	6.30 × 10⁻³	4.20 × 10⁻³	3.15 × 10⁻³	(4,3.1477 × 10⁻³)
	40	9.53 × 10⁻³	4.76 × 10⁻³	3.17 × 10⁻³	2.38 × 10⁻³	(4,2.3788 × 10⁻³)
ϕ_a(t) K = 1	20	6.84 × 10⁻⁹	3.36 × 10⁻⁹	8.00 × 10⁻⁹	3.32 × 10⁻⁸	(2,8.1966 × 10⁻¹¹)
	30	6.65 × 10⁻¹³	3.34 × 10⁻¹³	1.79 × 10⁻¹²	8.00 × 10⁻¹²	(2,3.1491 × 10⁻¹⁵)
	40	3.50 × 10⁻¹⁵	4.87 × 10⁻¹⁵	5.25 × 10⁻¹⁵	5.76 × 10⁻¹⁵	(1,5.6380 × 10⁻¹⁶)
ϕ_a(t) K = 3/2	20	7.10 × 10⁻⁵	3.55 × 10⁻⁵	2.34 × 10⁻⁵	1.76 × 10⁻⁵	(4,1.0517 × 10⁻⁵)
	30	2.20 × 10⁻⁵	1.09 × 10⁻⁵	7.25 × 10⁻⁶	5.42 × 10⁻⁶	(4,3.2707 × 10⁻⁶)
	40	5.43 × 10⁻⁶	3.14 × 10⁻⁶	4.22 × 10⁻⁷	3.15 × 10⁻⁷	(4,1.2510 × 10⁻⁷)

Example 4.5. Finally, in this example we consider the Flierl-Petviashvili (FP) equation [17, 18]. The FP monopole y(x) is the radially symmetric solution to the equation

()

where the boundary condition is y(∞) = 0. Flierl [17] and Petviashvili [18] independently derived this equation as a model for vortex solitons in the ocean and in plasmas, respectively. Equation (4.14) was investigated by Boyd in [20] and later by Wazwaz in [49].

In this problem the FP monopole α is an unknown value that should be determined. Boyd [20] and Wazwaz [49] employed the boundary condition y(∞) = 0 in combination with the Pade approximants in order to approximate the FP monopole α. In this paper, however, we do not use the boundary condition y(∞) = 0. In fact, here, we aim to solve the following problem:

()

and then we approximate the value of α = y(0).

Our procedure for solving this problem and approximating the FP monopole α is obtained by a little change in our CGR scheme as follows. After expressing the FP equation in (4.15) in terms of t using (2.7), in the first stage, we set N = 5 and evaluate the mentioned equation at collocation points (t₁, t₂, …, t₅) (in general (t₁, t₂, …, t_N)) and noncollocated point t₆ = 1 (in general t_N+1 = 1), by which in combination with the initial slope condition in (3.21) we obtain a system of 7 (in general N + 2) algebraic equations for unknowns Y₀, Y₁, …, Y₆ (in general Y₀, Y₁, …, Y_N+1). Note that evaluating (2.7) at noncollocated point t_N+1 = 1 is not versus our CGR collocation scheme because at t_N+1 = 1 the coefficients of Y^′(t_N+1) and Y^′′(t_N+1) in (2.7) using the transformations of this paper will be zero and there is no need to approximate these derivatives based on collocation points. For N = 5, the obtained system of algebraic equations has 64 (in general 2^N+1) solution sets. These solution sets can be obtained using any symbolic software. We obtained them using “Mathematica” with the command “NSolve.” Now we evaluate each of the solution sets. The complex solution sets should be discarded. Next, as Boyd [20] stated from physical grounds, the solution y(x) for FP equation is negative and increasing; thus, between the real solution sets, after discarding the solution sets that are oscillatory or contain positive elements, the acceptable solution set is obtained. We then increase N by 5, but in this stage we solve the obtained system of algebraic equations using Newton’s iterative method and utilize the approximate solution at stage one as initial guess for Newton’s method. We continue this approach until the results for α ≈ Y₀ are similar up to a required number of decimal places for two consecutive stages.

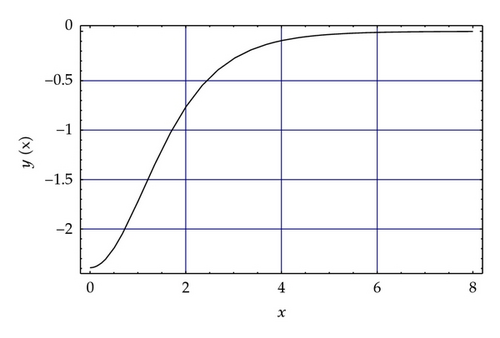
Solving this problem using the above procedure and using ϕ_a with K = 1 and N = 5 reveals that the exact solution of the FP equation decays almost exponentially; thus, for this problem both algebraic and logarithmic changes of variables would work. In this example we set the mapping parameter L = 2, which provides faster convergence. Table 7 exhibits the approximated and exact values of FP monopole α. It is observed that using both algebraic and logarithmic transformations of this paper, the approximations converge monotonically to the exact α = y(0) as N increases. However, the algebraic transformation ϕ_a with K = 1/2 provides more rapid convergence in comparison with other transformations. Moreover, it is seen that our procedure produces more accurate results than those obtained in [20, 49] by using the Pade approximants. The computational result for y(x) using the present CGR scheme with N = 40, L = 2, ϕ_a, and K = 1/2 is shown in Figure 2.

Table 7. Approximate and exact values of α = y(0) for Example 4.5.

N	ϕ_a (K = 1/2)	ϕ_a (K = 1)	ϕ_a (K = 3/2)	ϕ_l
5	−2.416296577	−2.488733071	−2.221866799	−2.385636308
10	−2.391957269	−2.391760175	−2.387175116	−2.391957083
15	−2.391956196	−2.391955001	−2.391806999	−2.391956290
20	−2.391956398	−2.391956374	−2.391958288	−2.391956428
25	−2.391956405	−2.391956410	−2.391956155	−2.391956397
30	−2.391956403	−2.391956404	−2.391956426	−2.391956405
35	−2.391956403	−2.391956403	−2.391956405	−2.391956402
40	−2.391956403	−2.391956403	−2.391956403	−2.391956404
Wazwaz [49], Pade [8/8]	−2.3922139
Boyd [20], Pade [10/10]	−2.3919746
Exact	−2.3919564

5. Conclusions

Two collocation methods have been presented for the numerical solution of nonlinear semi-infinite-domain two-point boundary value problems and initial value problems using global collocation at Chebyshev-Gauss and Chebyshev-Gauss-Radau points. It was shown that the transformed problems that arise from a transformation followed by Gauss or Radau collocation include an approximation to the solution at x = +∞. The results of this paper indicate that the use of Chebyshev-Gauss and Chebyshev-Gauss-Radau points lead to accurate approximations to continuous nonlinear semi-infinite-domain boundary and initial value problems. Algebraic and logarithmic transformations were utilized and a new category of algebraic transformations was introduced. For problems whose exact solution decays algebraically, the transformations were relatively insensitive to the mapping parameter L. Furthermore, by tuning the transformations used to map the semi-infinite domain [0, ∞) to a finite interval, it was possible to improve the accuracy in the discrete approximation, significantly. However, the proper choice of transformation should be based on the criterions that the solution to the problem be smooth in the transformed coordinate and the transformation should adjust spacing of the collocation points based on the decay rate of the solution.

References

1 Agarwal R. P. and O′Regan D., Infinite interval problems modeling the flow of a gas through a semi-infinite porous medium, Studies in Applied Mathematics. (2002) 108, no. 3, 245–257, https://doi.org/10.1111/1467%2D9590.01411, 1895284, ZBL1152.34315.
10.1111/1467-9590.01411
Web of Science® Google Scholar
2 Kidder R. E., Unsteady flow of gas through a semi-infinite porous medium, Journal of Applied Mechanics. (1957) 24, 329–332, 0092536, ZBL0078.40903.
10.1115/1.4011542
Google Scholar
3 Hashim I. and Wilson S. K., The onset of oscillatory Marangoni convection in a semi-infinitely deep layer of fluid, Zeitschrift für Angewandte Mathematik und Physik. (1999) 50, no. 4, 546–558, https://doi.org/10.1007/s000330050165, 1709703, ZBL0938.76027.
10.1007/s000330050165
Web of Science® Google Scholar
4 Na T. Y., Computational Methods in Engineering Boundary Value Problems, 1979, Academic Press, New York, NY, USA, 561710.
Google Scholar
5 Agarwal R. P. and O′Regan D., Singular problems on the infinite interval modelling phenomena in draining flows, IMA Journal of Applied Mathematics. (2001) 66, no. 6, 621–635, https://doi.org/10.1093/imamat/66.6.621, 1869408, ZBL1073.34506.
10.1093/imamat/66.6.621
Web of Science® Google Scholar
6 Agarwal R. P. and O′Regan D., An infinite interval problem arising in circularly symmetric deformations of shallow membrane caps, International Journal of Non-Linear Mechanics. (2004) 39, no. 5, 779–784, https://doi.org/10.1016/S0020%2D7462(03)00041%2D6, 2036912.
10.1016/S0020-7462(03)00041-6
Web of Science® Google Scholar
7 Dickey R. W., Membrane caps under hydrostatic pressure, Quarterly of Applied Mathematics. (1988) 46, no. 1, 95–104, 934684, ZBL0644.73061.
10.1090/qam/934684
Web of Science® Google Scholar
8 Dickey R. W., Rotationally symmetric solutions for shallow membrane caps, Quarterly of Applied Mathematics. (1989) 47, no. 3, 571–581, 1012280, ZBL0683.73022.
10.1090/qam/1012280
Web of Science® Google Scholar
9 Greguš M., On a special boundary value problem, Acta Mathematica. (1982) 40, 161–168, 686972, ZBL0512.34014.
Google Scholar
10 Agarwal R. P. and O′Regan D., Infinite interval problems modeling phenomena which arise in the theory of plasma and electrical potential theory, Studies in Applied Mathematics. (2003) 111, no. 3, 339–358, https://doi.org/10.1111/1467%2D9590.t01%2D1%2D00237, 1999644, ZBL1141.34313.
10.1111/1467-9590.t01-1-00237
Web of Science® Google Scholar
11 Erbe L. and Schmitt K., On radial solutions of some semilinear elliptic equations, Differential and Integral Equations. (1988) 1, no. 1, 71–78, 920490, ZBL0721.35020.
10.57262/die/1371747583
Google Scholar
12 Granas A., Guenther R. B., Lee J. W., and O′Regan D., Boundary value problems on infinite intervals and semiconductor devices, Journal of Mathematical Analysis and Applications. (1986) 116, no. 2, 335–348, https://doi.org/10.1016/S0022%2D247X(86)80002%2D6, 842804, ZBL0594.34019.
10.1016/S0022-247X(86)80002-6
Web of Science® Google Scholar
13 Agarwal R. P. and O′Regan D., Infinite interval problems arising in non-linear mechanics and non-Newtonian fluid flows, International Journal of Non-Linear Mechanics. (2003) 38, no. 9, 1369–1376, https://doi.org/10.1016/S0020%2D7462(02)00076%2D8, 1991507.
10.1016/S0020-7462(02)00076-8
Web of Science® Google Scholar
14 Chandrasekhar S., An Introduction to the Study of Stellar Structure, 1957, Dover, New York, NY, USA, 0092663.
Google Scholar
15 Davis H. T., Introduction to Nonlinear Differential and Integral Equations, 1962, Dover, New York, NY, USA, 0181773.
Google Scholar
16 Richardson O. U., The Emission of Electricity from Hot Bodies, 1921, London, UK.
Google Scholar
17 Flierl G. R., Baroclinic solitary waves with radial symmetry, Dynamics of Atmospheres and Oceans. (1979) 3, no. 1, 15–38, 2-s2.0-0001916570.
10.1016/0377-0265(79)90034-4
Web of Science® Google Scholar
18 Petviashvili V. I., Red spot of Jupiter and the drift soliton in a plasma, JETP Letters. (1981) 32, 619–622.
Web of Science® Google Scholar
19 Lentini M. and Keller H. B., Boundary value problems on semi-infinite intervals and their numerical solution, SIAM Journal on Numerical Analysis. (1980) 17, no. 4, 577–604, https://doi.org/10.1137/0717049, 584732, ZBL0465.65044.
10.1137/0717049
Web of Science® Google Scholar
20 Boyd J., Padé approximant algorithm for solving nonlinear ordinary differential equation boundary value problems on an unbounded domain, Computers in Physics. (1997) 11, no. 3, 299–303.
10.1063/1.168606
Web of Science® Google Scholar
21 Fazio R., A survey on free boundary identification of the truncated boundary in numerical BVPs on infinite intervals, Journal of Computational and Applied Mathematics. (2002) 140, no. 1-2, 331–344, https://doi.org/10.1016/S0377%2D0427(01)00526%2DX, 1934448.
10.1016/S0377-0427(01)00526-X
Web of Science® Google Scholar
22 Ravi Kanth A. S. V. and Reddy Y. N., A numerical method for solving two-point boundary value problems over infinite intervals, Applied Mathematics and Computation. (2003) 144, no. 2-3, 483–494, https://doi.org/10.1016/S0096%2D3003(02)00422%2D8, 1994086, ZBL1024.65060.
10.1016/S0096-3003(02)00422-8
Web of Science® Google Scholar
23 Chen B., Tong L., and Gu Y., Precise time integration for linear two-point boundary value problems, Applied Mathematics and Computation. (2006) 175, no. 1, 182–211, https://doi.org/10.1016/j.amc.2005.08.001, 2216334, ZBL1088.65070.
10.1016/j.amc.2005.08.001
Web of Science® Google Scholar
24 Coulaud O., Funaro D., and Kavian O., Laguerre spectral approximation of elliptic problems in exterior domains, Computer Methods in Applied Mechanics and Engineering. (1990) 80, no. 1–3, 451–458, https://doi.org/10.1016/0045%2D7825(90)90050%2DV, 1067965, ZBL0734.73090.
10.1016/0045-7825(90)90050-V
Web of Science® Google Scholar
25 Funaro D., Computational aspects of pseudospectral Laguerre approximations, Applied Numerical Mathematics. (1990) 6, no. 6, 447–457, https://doi.org/10.1016/0168%2D9274(90)90003%2DX, 1087134, ZBL0708.65072.
10.1016/0168-9274(90)90003-X
Web of Science® Google Scholar
26 Shen J., Stable and efficient spectral methods in unbounded domains using Laguerre functions, SIAM Journal on Numerical Analysis. (2000) 38, no. 4, 1113–1133, https://doi.org/10.1137/S0036142999362936, 1786133, ZBL0979.65105.
10.1137/S0036142999362936
Web of Science® Google Scholar
27 Funaro D. and Kavian O., Approximation of some diffusion evolution equations in unbounded domains by Hermite functions, Mathematics of Computation. (1991) 57, no. 196, 597–619, https://doi.org/10.2307/2938707, 1094949, ZBL0764.35007.
10.1090/S0025-5718-1991-1094949-X
Web of Science® Google Scholar
28 Guo B.-Y., Error estimation of Hermite spectral method for nonlinear partial differential equations, Mathematics of Computation. (1999) 68, no. 227, 1067–1078, https://doi.org/10.1090/S0025%2D5718%2D99%2D01059%2D5, 1627789, ZBL0918.65069.
10.1090/S0025-5718-99-01059-5
Web of Science® Google Scholar
29 Parand K., Dehghan M., Rezaei A. R., and Ghaderi S. M., An approximation algorithm for the solution of the nonlinear Lane-Emden type equations arising in astrophysics using Hermite functions collocation method, Computer Physics Communications. (2010) 181, no. 6, 1096–1108, https://doi.org/10.1016/j.cpc.2010.02.018, 2644949, ZBL1216.65098.
10.1016/j.cpc.2010.02.018
CAS Web of Science® Google Scholar
30 Boyd J. P., Chebyshev and Fourier Spectral Methods, 2000, 2nd edition, Dover, New York, NY, USA, 1874071.
Google Scholar
31 Christov C. I., A complete orthonormal system of functions in L²(−∞, ∞) space, SIAM Journal on Applied Mathematics. (1982) 42, no. 6, 1337–1344, https://doi.org/10.1137/0142093, 678221, ZBL0562.33009.
10.1137/0142093
Web of Science® Google Scholar
32 Boyd J. P., Spectral methods using rational basis functions on an infinite interval, Journal of Computational Physics. (1987) 69, no. 1, 112–142, https://doi.org/10.1016/0021%2D9991(87)90158%2D6, 892255, ZBL0615.65090.
10.1016/0021-9991(87)90158-6
Web of Science® Google Scholar
33 Boyd J. P., Orthogonal rational functions on a semi-infinite interval, Journal of Computational Physics. (1987) 70, no. 1, 63–88, https://doi.org/10.1016/0021%2D9991(87)90002%2D7, 888932, ZBL0614.42013.
10.1016/0021-9991(87)90002-7
Web of Science® Google Scholar
34 Guo B.-Y., Shen J., and Wang Z.-Q., A rational approximation and its applications to differential equations on the half line, Journal of Scientific Computing. (2000) 15, no. 2, 117–147, https://doi.org/10.1023/A:1007698525506, 1827574, ZBL0984.65104.
10.1023/A:1007698525506
Google Scholar
35 Boyd J. P., Rangan C., and Bucksbaum P. H., Pseudospectral methods on a semi-infinite interval with application to the hydrogen atom: a comparison of the mapped Fourier-sine method with Laguerre series and rational Chebyshev expansions, Journal of Computational Physics. (2003) 188, no. 1, 56–74, 2-s2.0-0038346445, https://doi.org/10.1016/S0021%2D9991(03)00127%2DX.
10.1016/S0021-9991(03)00127-X
CAS Web of Science® Google Scholar
36 Chowdhury M. S. H. and Hashim I., Solutions of Emden-Fowler equations by homotopy-perturbation method, Nonlinear Analysis: Real World Applications. (2009) 10, no. 1, 104–115, https://doi.org/10.1016/j.nonrwa.2007.08.017, 2451694, ZBL1154.34306.
10.1016/j.nonrwa.2007.08.017
Web of Science® Google Scholar
37 Parand K. and Taghavi A., Rational scaled generalized Laguerre function collocation method for solving the Blasius equation, Journal of Computational and Applied Mathematics. (2009) 233, no. 4, 980–989, https://doi.org/10.1016/j.cam.2009.08.106, 2557289.
10.1016/j.cam.2009.08.106
Web of Science® Google Scholar
38 Abbasbandy S., A numerical solution of Blasius equation by Adomian′s decomposition method and comparison with homotopy perturbation method, Chaos, Solitons and Fractals. (2007) 31, no. 1, 257–260, 2-s2.0-33745859755, https://doi.org/10.1016/j.chaos.2005.10.071.
10.1016/j.chaos.2005.10.071
Web of Science® Google Scholar
39 Parand K., Abbasbandy S., Kazem S., and Rezaei A. R., Comparison between two common collocation approaches based on radial basis functions for the case of heat transfer equations arising in porous medium, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 3, 1396–1407, 2-s2.0-77957361317, https://doi.org/10.1016/j.cnsns.2010.07.011.
10.1016/j.cnsns.2010.07.011
Web of Science® Google Scholar
40 Parand K., Abbasbandy S., Kazem S., and Rad J. A., A novel application of radial basis functions for solving a model of first-order integro-ordinary differential equation, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 11, 4250–4258, https://doi.org/10.1016/j.cnsns.2011.02.020, 2806736, ZBL1222.65150.
10.1016/j.cnsns.2011.02.020
Web of Science® Google Scholar
41 Grosch C. E. and Orszag S. A., Numerical solution of problems in unbounded regions: coordinate transforms, Journal of Computational Physics. (1977) 25, no. 3, 273–295, 0488870, https://doi.org/10.1016/0021%2D9991(77)90102%2D4, ZBL0403.65050.
10.1016/0021-9991(77)90102-4
Web of Science® Google Scholar
42 Boyd J. P., The optimization of convergence for Chebyshev polynomial methods in an unbounded domain, Journal of Computational Physics. (1982) 45, no. 1, 43–79, https://doi.org/10.1016/0021%2D9991(82)90102%2D4, 650425, ZBL0488.65035.
10.1016/0021-9991(82)90102-4
Web of Science® Google Scholar
43 Guo B.-Y., Gegenbauer approximation and its applications to differential equations on the whole line, Journal of Mathematical Analysis and Applications. (1998) 226, no. 1, 180–206, https://doi.org/10.1006/jmaa.1998.6025, 1646485, ZBL0913.41020.
10.1006/jmaa.1998.6025
Web of Science® Google Scholar
44 Guo B.-Y., Jacobi spectral approximations to differential equations on the half line, Journal of Computational Mathematics. (2000) 18, no. 1, 95–112, 1741177, ZBL0948.65071.
Web of Science® Google Scholar
45 Guo B.-Y., Jacobi approximations in certain Hilbert spaces and their applications to singular differential equations, Journal of Mathematical Analysis and Applications. (2000) 243, no. 2, 373–408, https://doi.org/10.1006/jmaa.1999.6677, 1741531, ZBL0951.41006.
10.1006/jmaa.1999.6677
Web of Science® Google Scholar
46 Abramowitz M. and Stegun I., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 1965, Dover, New York, NY, USA, 1225604.
Google Scholar
47 Costa B. and Don W. S., On the computation of high order pseudospectral derivatives, Applied Numerical Mathematics. (2000) 33, no. 1–4, 151–159, https://doi.org/10.1016/S0168%2D9274(99)00078%2D1, 1770248.
10.1016/S0168-9274(99)00078-1
Web of Science® Google Scholar
48 Countryman M. and Kannan R., Nonlinear boundary value problems on semi-infinite intervals, Computers & Mathematics with Applications. (1994) 28, no. 10–12, 59–75, https://doi.org/10.1016/0898%2D1221(94)00186%2D3, 1300682, ZBL0810.65080.
10.1016/0898-1221(94)00186-3
Web of Science® Google Scholar
49 Wazwaz A.-M., Padé approximants and Adomian decomposition method for solving the Flierl-Petviashivili equation and its variants, Applied Mathematics and Computation. (2006) 182, no. 2, 1812–1818, https://doi.org/10.1016/j.amc.2006.06.018, 2282623, ZBL1107.65061.
10.1016/j.amc.2006.06.018
Web of Science® Google Scholar
50 Bender C. M., Milton K. A., Pinsky S. S., and SimmonsL. M.Jr., A new perturbative approach to nonlinear problems, Journal of Mathematical Physics. (1989) 30, no. 7, 1447–1455, https://doi.org/10.1063/1.528326, 1002247, ZBL0684.34008.
10.1063/1.528326
Web of Science® Google Scholar

Citing Literature

All articles

Analysis of IVPs and BVPs on Semi-Infinite Domains via Collocation Methods

Abstract

1. Introduction

2. Problem Statement and Domain Transformation