Generalized Lower and Upper Approximations in Quantales
Abstract
We introduce the concepts of set-valued homomorphism and strong set-valued homomorphism of a quantale which are the extended notions of congruence and complete congruence, respectively. The properties of generalized lower and upper approximations, constructed by a set-valued mapping, are discussed.
1. Introduction
The concept of Rough set was introduced by Pawlak [1] as a mathematical tool for dealing with vagueness or uncertainty. In Pawlak’s rough sets, the equivalence classes are the building blocks for the construction of the lower and upper approximations. It soon invoked a natural question concerning a possible connection between rough sets and algebraic systems. Biswas and Nanda [2] introduced the notion of rough subgroups. Kuroki [3] and Qimei [4] introduced the notions of a rough ideal and a rough prime ideal in a semigroup, respectively. Davvaz in [5] introduced the notion of rough subring with respect to an ideal of a ring. Rough modules have been investigated by Davvaz and Mahdavipour [6]. Rasouli and Davvaz studied the roughness in MV-algebra [7]. In [8–12], the roughness of various hyperstructures are discussed. Further, some authors consider the rough set in a fuzzy algebraic system, see [13–16]. The concept of quantale was introduced by Mulvey [17] in 1986 with the purpose of studying the spectrum of C*-algebra, as well as constructive foundations for quantum mechanics. There are abundant contents in the structure of quantales, because quantale can be regarded as the generalization of frame. Since quantale theory provides a powerful tool in studying noncommutative structures, it has wide applications, especially in studying noncommutative C*-algebra theory, the ideal theory of commutative ring, linear logic, and so on. The quantale theory has aroused great interests of many researchers, and a great deal of new ideas and applications of quantale have been proposed in twenty years [18–24].
The majority of studies on rough sets for algebraic structures such as semigroups, groups, rings, and modules have been concentrated on a congruence relation. An equivalence relation is sometimes difficult to be obtained in real-world problems due to the vagueness and incompleteness of human knowledge. From this point of view, Davvaz [25] introduced the concept of set-valued homomorphism for groups. And then, Yamak et al. [26, 27] introduced the concepts of set-valued homomorphism and strong set-valued homomorphism of a ring and a module. In this paper, the concepts of set-valued homomorphism and strong set-valued homomorphism in quantales are introduced. We discuss the properties of generalized lower and upper approximations in quantales.
2. Preliminaries
In this section, we give some basic notions and results about quantales and rough set theory (see [19, 22, 25, 28]), which will be necessary in the next sections.
Definition 2.1. A quantale is a complete lattice Q with an associative binary operation ∘ satisfying
An element e ∈ Q is called a left (right) unit if and only if e∘a = a (a∘e = a), e is called a unit if it is both a right and left unit.
A quantale Q is called a commutative quantale if a∘b = b∘a for all a, b ∈ Q.
A quantale Q is called an idempotent quantale if a∘a = a for all a ∈ Q.
A subset S of Q is called a subquantale of Q if it is closed under ∘ and arbitrary sups.
In a quantale Q, we denote the top element of Q by 1 and the bottom by 0. For A, B⊆Q, we write A∘B to denote the set {a∘b∣a ∈ A, b ∈ B}, A∨B to denote {a∨b∣a ∈ A, b ∈ B} and .
Definition 2.2. Let Q be a quantale, a subset ∅ ≠ I⊆Q is called a left (right) ideal of Q if
- (1)
a, b ∈ I implies a∨b ∈ I,
- (2)
a ∈ I, b ∈ Q and b ≤ a imply b ∈ I for all,
- (3)
a ∈ Q and x ∈ I imply a∘x ∈ I (x∘a ∈ I).
A subset I⊆Q is called an ideal if it is both a left and a right ideal.
Let X be a subset of Q, we write ↓X = {y ∈ Q∣y ≤ x for some x ∈ X}, X is a lower set if and only if X = ↓X. It is obvious that an ideal I is a directed lower set. For every (left, right) ideal I of Q, it is easy to see that 0 ∈ I.
An ideal of Q is called a prime ideal if a∘b ∈ I implies a ∈ I or b ∈ I for all a, b ∈ Q.
An ideal I of Q is called a semi-prime ideal if a∘a ∈ I implies a ∈ I for all a ∈ Q.
An ideal I of Q (I ≠ Q) is called a primary ideal if for all a, b ∈ Q, a∘b ∈ I and a ∉ I imply bn ∈ I for some n > 0. ().
Definition 2.3. A nonempty subset M⊆Q is called an m-system of Q, if for all a, b ∈ M, ↓(a∘1∘b)∩M ≠ ∅.
A nonempty subset S⊆Q is called a multiplicative set of Q, if a∘b ∈ S for all a, b ∈ S.
Every ideal of Q is both an m-system and a multiplicative set.
Definition 2.4. Let Q be a quantale, an equivalence relation θ on L is called a congruence on Q if for all a, b, c, d, ai, bi ∈ Q (i ∈ I), we have
- (1)
aθb, cθd⇒(a∘c)θ(b∘d),
- (2)
.
Definition 2.5. Let Q be a quantale, a congruence θ on Q is called a complete congruence, if
- (1)
[a] θ∘[b] θ = [a∘b] θ for all a, b ∈ Q,
- (2)
for all ai ∈ Q (i ∈ I).
Definition 2.6. Let (Q1, ∘1) and (Q2, ∘2) be two quantales. A map f : Q1 → Q2 is said to be a homomorphism if
- (1)
f(a ∘1 b) = f(a)∘2f(b) for all a, b ∈ Q1;
- (2)
for all ai ∈ Q1 (i ∈ I).
Definition 2.7. Let U and W be two nonempty universes. Let T be a set-valued mapping given by T : U → P(W), where P(W) denotes the set of all subsets of W. Then the triple (U, W, T) is referred to as a generalized approximation space. For any set A⊆W, the generalized lower and upper approximations, T−(A) and T−(A), are defined by
The pair (T−(A), T−(A)) is referred to as a generalized rough set.
From the definition, the following theorems can be easily derived.
Theorem 2.8. Let U, W be nonempty universes and T : U → P*(W) be a set-valued mapping, where P*(W) denotes the set of all nonempty subsets of W. If A⊆W, then T−(A)⊆T−(A).
If W = U and RT = {(x, y)∣y ∈ T(x)} is an equivalence relation on U, then the pair (U, RT) is the Pawlak approximation space. Therefore, a generalized rough set is an extended notion of Pawlak’s rough set.
Theorem 2.9. Let (U, W, T) be a generalized approximation space, its lower and upper approximation operators satisfy the following properties. For all A, B ∈ P(W),
- (1)
T−(A) = (T−(Ac)) c, T−(A) = (T−(Ac)) c,
- (2)
T−(W) = U, T−(∅) = ∅,
- (3)
T−(A∩B) = T−(A)∩T−(B), T−(A ∪ B) = T−(A) ∪ T−(B),
- (4)
A⊆B⇒T−(A)⊆T−(B), T−(A)⊆T−(B),
- (5)
T−(A ∪ B)⊇T−(A) ∪ T−(B), T−(A∩B)⊆T−(A)∩T−(B),
3. Generalized Rough Subsets in Quantales
In this paper, (Q1, ∘1) and (Q2, ∘2) are two quantales.
Theorem 3.1. Let T : Q1 → P(Q2) be a set-valued mapping and ∅ ≠ A, B⊆Q2. Then
- (1)
T−(A) ∪ T−(B)⊆T−(A∨B), if 0 ∈ A∩B,
- (2)
T−(A) ∪ T−(B)⊆T−(A ∘2 B), if e ∈ A∩B,
- (3)
T−(A)∩T−(B)⊆T−(A∨B),
- (4)
T−(A)∩T−(B)⊆T−(A∨B), if Q2 is an idempotent quantale,
- (5)
T−(A) ∪ T−(B)⊆T−(A∨B), if 0 ∈ A∩B,
- (6)
T−(A) ∪ T−(B)⊆T−(A ∘2 B), if e ∈ A∩B.
Proof. (1) Suppose that a ∈ A, we have a = a∨0 ∈ A∨B for 0 ∈ B. So A⊆A∨B. Similarly, B⊆A∨B. So A ∪ B⊆A∨B. By Theorem 2.9, we have T−(A) ∪ T−(B) = T−(A ∪ B)⊆T−(A∨B).
(2) Suppose that a ∈ A, we have a = a ∘2 e ∈ A ∘2 B for e ∈ B. So A⊆A ∘2 B. Similarly, B⊆A ∘2 B. So A ∪ B⊆A ∘2 B. By Theorem 2.9, we have T−(A) ∪ T−(B) = T−(A ∪ B)⊆T−(A ∘2 B).
(3) It is obvious that A∩B⊆A∨B. By Theorem 2.9, we have T−(A) ∩ T−(B) = T−(A ∩ B)⊆T−(A∨B).
(4) Since Q2 is an idempotent quantale, we have A∩B⊆A∘B. By Theorem 2.9, we have T−(A)∩T−(B) = T−(A∩B)⊆T−(A ∘2 B).
(5) and (6) The proofs are similar to (1) and (2), respectively.
Definition 3.2. A set-valued mapping T : Q1 → P(Q2) is called a set-valued homomorphism if
- (1)
T(a) ∘2 T(b)⊆T(a ∘1 b) for all a, b ∈ Q1,
- (2)
for all ai ∈ Q1(i ∈ I).
T is called a strong set-valued homomorphism if the equalities in (1), (2) hold.
Example 3.3. (1) Let θ be a congruence on Q2. Then the set-valued mapping T : Q1 → P(Q2) defined by T(x) = [x] θ is a set-valued homomorphism but not necessarily a strong set-valued homomorphism. If θ is complete, then T is a strong set-valued homomorphism.
(2) Let f be a quantale homomorphism from Q1 to Q2. Then the set-valued mapping T : Q1 → P(Q2) defined by T(a) = {f(a)} is a strong set-valued homomorphism.
Theorem 3.4. Let T : Q1 → P(Q2) be a set-valued homomorphism and ∅ ≠ A, B⊆Q2. Then
- (1)
T−(A)∨T−(B)⊆T−(A∨B),
- (2)
T−(A) ∘1 T−(B)⊆T−(A ∘2 B),
- (3)
T−(A)∩T−(B)⊆T−(A∨B),
- (4)
T−(A)∩T−(B)⊆T−(A ∘2 B), if Q1 is an idempotent quantale.
Proof. (1) Suppose that c ∈ T−(A)∨T−(B), there exist a ∈ T−(A), b ∈ T−(B) such that c = a∨b. So there exist x ∈ A∩T(a) and y ∈ B∩T(b). Hence x∨y ∈ A∨B and x∨y ∈ T(a)∨T(b). Since T is a set-valued homomorphism, we have x∨y ∈ T(a∨b). Therefore, T(a∨b)∩(A∨B) ≠ ∅ which implies that c = a∨b ∈ T−(A∨B).
(2) The proof is similar to (1).
(3) Suppose that x ∈ T−(A) ∩ T−(B), there exist a ∈ A∩T(x) and b ∈ B∩T(x). Since T is a set-valued homomorphism, we have a∨b ∈ T(x)∨T(x)⊆T(x). So a∨b ∈ T(x)∩(A∨B) which implies that x ∈ T−(A∨B).
(4) Suppose that x ∈ T−(A) ∩ T−(B), there exist a ∈ A ∩ T(x) and b ∈ B ∩ T(x). Since T is a set-valued homomorphism and Q1 is idempotent, we have a∨b ∈ T(x) ∘2 T(x)⊆T(x ∘1 x) = T(x). So a∨b ∈ T(x)∩(A∨B) which implies that x ∈ T−(A ∘2 B).
Theorem 3.5. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and ∅ ≠ A, B⊆Q2. Then
- (1)
T−(A)∨T−(B)⊆T−(A∨B),
- (2)
T−(A) ∘1 T−(B)⊆T−(A ∘2 B).
Proof. (1) Suppose that c ∈ T−(A)∨T−(B), there exist a ∈ T−(A), b ∈ T−(B) such that c = a∨b. Hence T(a)⊆A and T(b)⊆B. Since T is a strong set-valued homomorphism, we have T(a∨b) = T(a)∨T(b)⊆A∨B which implies that c = a∨b ∈ T−(A∨B).
(2) The proof is similar to (1).
4. Generalized Rough Ideals in Quantales
Theorem 4.1. Let T : Q1 → P(Q2) be a set-valued mapping. If I and J are, respectively, a right and a left ideal of Q2, then
- (1)
T−(I ∘2 J)⊆T−(I)∩T−(J),
- (2)
T−(I ∘2 J)⊆T−(I)∩T−(J),
- (3)
T−(I∧J)⊆T−(I)∩T−(J),
- (4)
T−(I)∧T−(J) = T−(I∧J),
- (5)
T−(I) ∪ T−(J)⊆T−(I∨J),
- (6)
T−(I) ∪ T−(J)⊆T−(I∨J).
If Q1 is an idempotent quantale and T is a set-valued homomorphism, then the equalities in (1)–(3) hold.
Proof. Since I and J are, respectively, a right and a left ideal of Q2, we have I ∘2 J⊆I∩J, I∧J = I∩J and o ∈ I∩J. By Theorem 2.9, we get the conclusion (1)–(4). By Theorem 3.1, we get (5) and (6).
If Q1 is idempotent, we first show that T−(I)∩T−(J)⊆T−(I ∘2 J). Suppose that x ∈ T−(I)∩T−(J), there exist y ∈ I, z ∈ J such that y, z ∈ T(x). So, y ∘2 z ∈ I ∘2 J and y ∘2 z ∈ T(x) ∘2 T(x). Since T is a set-valued homomorphism and Q1 is idempotent, we have y ∘2 z ∈ T(x ∘1 x) = T(x). Therefore, x ∈ T−(I ∘2 J). So the equality in (1) holds. Since Q1 is idempotent, we have I∩J⊆I ∘2 J. So I∩J = I ∘2 J = I∩J. By Theorem 2.9, we get T−(I ∘2 J) = T−(I∩J) = T−(I)∩T−(J). Since the equality in (1) holds, we have T−(I∧J) = T−(I ∘2 J) = T−(I)∩T−(J).
Lemma 4.2. Let T : Q1 → P(Q2) be a set-valued homomorphism. If A is a lower set of Q2, then T−(A) is a lower set of Q1.
Proof. Suppose x ≤ y ∈ T−(A), then T(y)⊆A. Let z ∈ T(x), a ∈ T(y), we have z∨a ∈ T(x)∨T(y)⊆T(x∨y) = T(y)⊆A. Since A is a lower set, we have z ∈ A. Therefore, T(x)⊆A which implies that x ∈ T−(A).
Lemma 4.3. Let T : Q1 → P(Q2) be a strong set-valued homomorphism. If A is a lower set of Q2, then T−(A) is a lower set of Q1.
Proof. Suppose that x ≤ y ∈ T−(A), there exists z ∈ T(y)∩A. Since T is a strong set-valued homomorphism, we have T(x)∨T(y) = T(x∨y) = T(y). So there exist a ∈ T(x), b ∈ T(y) such that z = a∨b. Since A is a lower set, we have a ∈ A. Thus T(x)∩A ≠ ∅ which follows that x ∈ T−(A).
Lemma 4.4. Let T : Q1 → P(Q2) be a set-valued homomorphism and A a nonempty subset of Q2. If A is closed under arbitrary (resp., finite) sups, then T−(A) is closed under arbitrary (resp., finite) sups.
Proof. Let B⊆T−(A). For each b ∈ B, we have b ∈ T−(A), then there exist xb ∈ T(b)∩A. Since T is a set-valued homomorphism, we have . And we have for A is closed under arbitrary sups. So T(⋁ B)∩A ≠ ∅ which implies that ⋁ B ∈ T−(A).
Lemma 4.5. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and A a nonempty subset of Q2. If A is closed under arbitrary (resp., finite) sups, then T−(A) is closed under arbitrary (resp., finite) sups.
Proof. Let B⊆T−(A). For each b ∈ B, we have T(b)⊆A. Since T is a strong set-valued homomorphism, we have T(⋁ B) = ⋁ T(B). Suppose z ∈ T(⋁ B) = ⋁ T(B), there exist xb ∈ T(b)⊆A (b ∈ B) such that . Since A is closed under arbitrary sups, we have . So T(⋁ B)⊆A which implies that ⋁ B ∈ T−(A).
Theorem 4.6. Let T : Q1 → P(Q2) be a set-valued homomorphism. If A is a subquantale of Q2, then T−(A) is a subquantale of Q1.
Proof. Since T is a set-valued homomorphism and A is a subquantale, by Theorems 3.4 and 2.9, we have T−(A) ∘1 T−(A)⊆T−(A ∘2 A)⊆T−(A). So, T−(A) is closed under ∘1.
Since A is closed under arbitrary sups, by Lemma 4.4, we get T−(A) is closed under arbitrary sups.
Theorem 4.7. Let T : Q1 → P(Q2) be a strong set-valued homomorphism. If A is a subquantale of Q2, then T−(A) is a subquantale of Q1.
Proof. The proof is similar to Theorem 4.6.
Theorem 4.8. Let T : Q1 → P*(Q2) be a strong set-valued homomorphism and I a right (left) ideal of Q2. Then T−(I) is, if it is nonempty, a right (left) ideal of Q1.
Proof. Suppose that a, b ∈ T−(I). Since I is closed under finite sups, by Lemma 4.4, we have T−(I) is closed under finite sups. So a∨b ∈ T−(I).
Since I is a lower set, by Lemma 4.3, we have T−(I) is a lower set.
Suppose a ∈ Q1, x ∈ T−(I), there exists y ∈ I∩T(x). Since I is a right ideal of Q2, we have y ∘2 b ∈ I for each b ∈ T(a)⊆Q2. So y ∘2 b ∈ T(x) ∘2 T(a)⊆T(x ∘1 a). Therefore, T(x ∘1 a)∩I ≠ ∅ which implies that x ∘1 a ∈ T−(I).
Theorem 4.9. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I a right (left) ideal of Q2. Then T−(I) is, if it is nonempty, a right (left) ideal of Q1.
Proof. Suppose a, b ∈ T−(I). Since I is closed under finite sups, by Lemma 4.5, we have T−(I) is closed under finite sups. So, a∨b ∈ T−(I).
Since I is a lower set, by Lemma 4.2, we have T−(I) is a lower set.
Suppose a ∈ Q1, x ∈ T−(I), we have T(x)⊆I. Let y ∈ T(x ∘1 a). Since T is a strong set-valued homomorphism, we have y ∈ T(x) ∘2 T(a), then there exist y1 ∈ T(x)⊆I, y2 ∈ T(a) such that y = y1 ∘2 y2. Since I is a right ideal, we have y = y1 ∘2 y2 ∈ I. Therefore, T(x ∘1 a)⊆I which implies that x∘1a ∈ T−(I).
Definition 4.10. A subset A⊆Q2 is called a generalized rough ideal (subquantale) of Q1 if T−(A) and T−(A) are ideals (subquantales) of Q1.
Corollary 4.11. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I an ideal (a subquantale) of Q2. If T−(I) and T−(I) are nonempty, then I is a generalized rough ideal (subquantale) of Q1.
From the above, we know that an ideal is a generalized rough ideal with respect to a strong set-valued homomorphism. The following example shows that the converse does not hold in general.
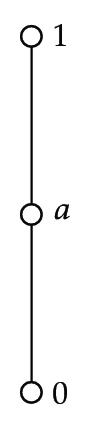
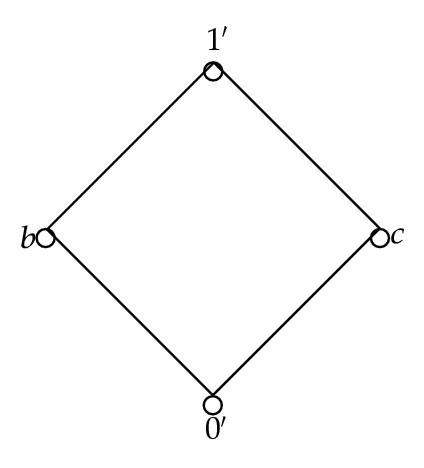
Example 4.12. Let Q1 = {0, a, 1} and Q2 = {0′, b, c, 1′} be quantales shown in Figures 1 and 2 and Tables 1 and 2.
Let T : Q1 → P(Q2) be a strong set-valued homomorphism as defined by T(0) = {0′}, T(a) = {b, c}, T(1) = {1′}. Let A = {0′, b, c}⊆Q2, B = {b, c}⊆Q2, then T−(A) = {0, a} = T−(A) and T−(B) = {a} = T−(B). It is obvious that A is a generalized rough ideal of Q1 but A is not an ideal of Q2 and B is a generalized rough subquantale of Q1 but B is not a subquantale of Q2.
| ∘1 | 0 | a | 1 |
|---|---|---|---|
| 0 | 0 | a | 1 |
| a | 0 | a | 1 |
| 1 | 0 | a | 1 |
| ∘2 | 0′ | b | c | 1′ |
|---|---|---|---|---|
| 0′ | 0′ | b | c | 1′ |
| b | 0′ | b | c | 1′ |
| c | 0′ | b | c | 1′ |
| 1′ | 0′ | b | c | 1′ |
Theorem 4.13. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I a prime ideal of Q2. Then T−(I) is, if it is nonempty, a prime ideal of Q1.
Proof. By Theorem 4.8, we get T−(I) is an ideal of Q1.
Let a ∘1 b ∈ T−(I), there exists x ∈ I∩T(a ∘1 b). Since T is a strong set-valued homomorphism, we have x ∈ T(a) ∘2 T(b), then there exist y ∈ T(a), z ∈ T(b) such that x = y ∘2 z ∈ I. Since I is a prime ideal of Q2, we have y ∈ I or z ∈ I. So T(a)∩I ≠ ∅ or T(b)∩I ≠ ∅ which implies that a ∈ T−(I) or b ∈ T−(I).
Theorem 4.14. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I a prime ideal of Q2. Then T−(I) is, if it is nonempty, a prime ideal of Q1.
Proof. By Theorem 4.9, we get T−(I) is an ideal of Q1.
Let a ∘1 b ∈ T−(I), we have T(a∘1b)⊆I. Since T is a strong set-valued homomorphism, we have T(a) ∘2 T(b)⊆I. We assume that a ∉ T−(I), then T(a)⊈I, there exists x ∈ T(a) but x ∉ I. If y ∈ T(b), then x ∘2 y ∈ T(a) ∘2 T(b)⊆I. Since I is a prime ideal of Q2, we have y ∈ I. Therefore, T(b)⊆I which implies that b ∈ T−(I).
We call I⊆Q2 is a generalized rough prime ideal of Q1 if T−(I) and T−(I) are ideals of Q1.
Theorem 4.15. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I a semiprime ideal of Q2. Then T−(I) is, if it is nonempty, a semiprime ideal of Q1.
Proof. By Theorem 4.9, we get T−(I) is an ideal of Q1.
Suppose that a ∘1 a ∈ T−(I), we have T(a ∘1 a)⊆I. Let x ∈ T(a), we have x ∘2 x ∈ T(a) ∘2 T(a)⊆T(a ∘1 a)⊆I. Since I is a semi-prime ideal, we have x ∈ I. So T(a)⊆I which implies that a ∈ T−(I).
Theorem 4.16. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I a primary ideal of Q2. Then T−(I) is, if T−(I) ≠ ∅ and T−(I) ≠ Q1, a primary ideal of Q1.
Proof. By Theorem 4.8, we get T−(I) is an ideal of Q1.
Suppose that a, b ∈ Q, a ∘1 b ∈ T−(I) and a ∉ T−(I), there exists x ∈ I∩T(a ∘1 b). Since T is a strong set-valued homomorphism, we have x ∈ T(a) ∘2 T(b), there exist y ∈ T(a), z ∈ T(b) such that x = y ∘2 z ∈ I. Since a ∉ T−(I), we get y ∉ I. Since I is a primary ideal, we have zn ∈ I for some n > 0 Since T is a strong set-valued homomorphism, we have zn ∈ T(bn). So T(bn)∩I ≠ ∅ which implies that bn ∈ T−(I).
Theorem 4.17. Let T : Q1 → P(Q2) be a strong set-valued homomorphism and I a primary ideal of Q2. Let Q2 be a commutative quantale and T(x) a finite set for each x ∈ Q1. Then T−(I) is, if T−(I) ≠ ∅ and T−(I) ≠ Q1, a primary ideal of Q1.
Proof. By Theorem 4.9, we get T−(I) is an ideal of Q1.
Suppose a, b ∈ Q, a ∘1 b ∈ T−(I) and a ∉ T−(I), then T(a ∘1 b)⊆I and T(a)⊈I. So there exists x ∈ T(a) with x ∉ I. We assume that T(b) = {y1, y2, …, ym}, then x ∘2 yi ∈ T(a) ∘2 T(b)⊆T(a ∘1 b)⊆I(i = 1,2, …, m). Since I is a primary ideal, there exists for some ni > 0 (i = 1,2, …, m). Let n = max {ni∣i = 1,2, …, m}. Since I is an ideal, we have . Let z ∈ T(bmbn) = T(b) mn. Since Q2 is commutative, there exists {i1, i2, …, is}⊆{1,2, …, m} such that with t1 + t2 + ⋯+ts = mn, where tj > 0 (j = 1,2, …, s). Assume that tj < n, (j = 1,2, …, s), then t1 + t2 + ⋯+ts < sn ≤ mn. It contradicts with t1 + t2 + ⋯+ts = mn. Therefore, there is 1 ≤ k ≤ s such that tk ≥ n, (j = 1,2, …, s), we have . Since I is an ideal, we get z ∈ I. Hence T(bmn)⊆I which implies that bmn ∈ T−(I).
Theorem 4.18. Let T : Q1 → P(Q2) be a set-valued homomorphism. If S is a multiplicative set of Q2, then T−(S) is, if it is nonempty, a multiplicative of Q1. If T is a strong set-valued homomorphism, then T−(S) is, if it is nonempty, a multiplicative of Q1.
Proof. Suppose that a, b ∈ T−(S), there exist x ∈ T(a)∩S, y ∈ T(b)∩S. Hence x∘y ∈ T(a)∘2T(b)⊆T(a∘1b). Since S is a multiplicative set, we have x∘2y ∈ S. Therefore, x∘2y ∈ T(a∘1b)∩S which implies that a∘1b ∈ T−(S).
Suppose a, b ∈ T−(S), then T(a)⊆S, T(b)⊆S. Let x ∈ T(a ∘1 b). Since T is a strong set-valued homomorphism, we have x ∈ T(a) ∘2 T(b). There exist y ∈ T(a)⊆S, z ∈ T(b)⊆S such that x = y ∘2 z. Since S is a multiplicative set, we have x = y ∘2 z ∈ S. So T(a ∘1 b)⊆S which implies that a ∘1 b ∈ T−(S).
We call A⊆Q2 a generalized rough multiplicative set (m-system) of Q1, if T−(A), T−(A) are multiplicative sets (m-systems) of Q1.
Theorem 4.19. Let T : Q1 → P*(Q2) be a set-valued homomorphism. If Q1 is commutative and A⊆Q2 with 1 ∉ T−(A), then the following statements are equivalent:
- (1)
A is a generalized rough prime ideal of Q1,
- (2)
A is a generalized rough ideal and Ac is a generalized rough multiplicative set of Q1,
- (3)
A is a generalized rough ideal and Ac is a generalized rough m-system of Q1.
Proof. (1)⇒(2): Since A is a generalized rough prime ideal of Q1, we get A is a generalized rough ideal of Q1 and T−(A), T−(A) are prime ideals of Q1. Now we show that T−(Ac) is a multiplicative set. Let a, b ∈ T−(Ac). By Theorem 2.9(1), we have a, b ∈ (T−(A)) c. Since T−(A) is a prime ideal, we have a ∘1 b ∉ T−(A) which implies that a ∘1 b ∈ (T−(A)) c = T−(Ac). So T−(Ac) is a multiplicative set. Similarly, T−(Ac) is a multiplicative set.
(2)⇒(3): Let a, b ∈ T−(Ac). Since 1 ∉ T−(A) and T(1) ≠ ∅, we have 1 ∈ T−(Ac). Since T−(Ac) is a multiplicative set, we have a ∘1 1 ∘1 b ∈ T−(Ac). So ↓(a ∘1 1 ∘1 b)∩T−(Ac) ≠ ∅. Therefore, T−(Ac) is an m-system. Similarly, we have T−(Ac) is a m-system.
(3)⇒(1): Let a ∘1 b ∈ T−(A). Suppose a ∉ T−(A) and b ∉ T−(A), then a, b ∈ (T−(A)) c = T−(Ac). Since T−(Ac) is an m-system, we have ↓(a ∘1 1 ∘1 b)∩T−(Ac) ≠ ∅. Thus ↓(a ∘1 1 ∘1 b)∩(T−(A)) c ≠ ∅. Since T−(A) is an ideal and Q1 is commutative, we have a ∘1 1 ∘1 b ∈ T−(A) and ↓(a ∘1 1 ∘1 b)⊆T−(A). It contradicts with ↓(a ∘1 1 ∘1 b)∩(T−(A)) c ≠ ∅. So, a ∈ T−(A) or b ∈ T−(A). Therefore, T−(A) is a prime ideal. Similarly, we have T−(A) as a prime ideal.
5. Conclusion
The Pawlak rough sets on the algebraic sets such as semigroups, groups, rings, modules, and lattices were mainly studied by a congruence relation. However, the generalized Pawlak rough set was defined for two universes and proposed on generalized binary relations. Can we extended congruence relations to two universes for algebraic sets? Therefore, Davvaz [25] introduced the concept of set-valued homomorphism for groups which is a generalization of the concept of congruence. In this paper, the concepts of set-valued homomorphism and strong set-valued homomorphism of quantales are introduced. We construct generalized lower and upper approximations by means of a set-valued mapping and discuss the properties of them. We obtain that the concept of generalized rough ideal (subquantale) is the extended notion of ideal (subquantale). Many results in [29] are the special case of the results in this paper. It is an interesting research topic of rough set, we will further study it in the future.
Acknowledgments
The authors are grateful to the reviewers for their valuable suggestions to improve the paper. This work was supported by the National Science Foundation of China (no. 11071061).




