We first investigate the structures of the square roots of a class of circulant matrices and give classifications of the square roots of these circulant matrices. Then, we develop several algorithms for computing their square roots. We show that our algorithms are faster than the standard algorithm which is based on the Schur decomposition.

1. Introduction

Circulant matrices and their generalizations arise in many areas of physics, electromagnetics, signal processing, statistics, and applied mathematics for the investigation of problems with periodicity properties [1–3]. Also, numerical solutions of certain types of elliptic and parabolic partial differential equations with periodic boundary conditions often involve linear systems Ax = b with A a circulant matrix. For recent years, the properties and applications of them have been extensively investigated [4–9].

A matrix X is said to be a square root of A if X² = A. The number of square roots varies from two (for a nonsingular Jordan block) to infinity (any involuntary matrix is a square root of the identity matrix). The key roles that the square root plays in, for example, the matrix sign function, the definite generalized eigenvalue problem, the polar decomposition, and the geometric mean, make it a useful theoretical and computational tool. The rich variety of methods for computing the matrix square root, with their widely differing numerical stability properties, is an interesting subject of study in their own right [10]. For these reasons, many authors became interested in the matrix square roots [11–14]. Although the theory of matrix square roots is rather complicated, simplifications occur for certain classes of matrices. Consider, for example, Hamiltonian matrices [15], semidefinite matrices [16], and so forth.

This paper is organized as follows. In Section 2, we review some basic properties of a class of circulant matrices. In Section 3, we investigate the structures of the square roots, then give the classifications of all the square roots of these circulant matrices. In Section 4, we develop some algorithms to compute the primary square roots of them. Finally, we present several numerical experiments in Section 5, exhibiting the efficiency of the proposed algorithms in terms of CPU time.

2. Preliminaries

Throughout this paper we denote the set of all n × n complex matrices by ℂ^n×n and the set of all real matrices by ℝ^n×n.

Definition 2.1 (see [4].)Let a = (a₀, a₁, …, a_n−1) ^T ∈ ℂⁿ and k ∈ ℂ. In a k-circulant matrix

()

Another equivalent definition of a k-circulant matrix is as follows: A ∈ ℂ^n×n is a k-circulant matrix if and only if A = G⁻¹AG, where G = Circ_k([0,1, 0, …, 0]).

Let n be an even number, A ∈ ℂ^n×n is a skew k-circulant matrix if A = −G⁻¹AG and a Hermitian k-circulant matrix if , where denotes the elementwise conjugate of the matrix A.

If the circulant matrix A is similar to a block diagonal matrix (even a diagonal matrix), that is, if there exists an invertible matrix P such that P⁻¹AP is a block diagonal matrix, the problem of computing the square roots of a circulant matrix can be reduced to that of computing the square roots of some small size matrices. It will help to reduce the costs of computation.

Lemma 2.2. If k ∈ ℝ, then all the matrices in Circ_k(a) are simultaneously diagonalizable, with the eigenvectors determined completely by k and a primitive nth root of unity.

We first review the structure and reducibility of above matrices. All the formulas become slightly more complicated when n is odd and k is a complex number; for simplicity, we restrict our attention to the case of even n = 2m and k ∈ ℝ. Using the partition, the n × n k-circulant matrix A can be described as

()

where B and C are m × m matrices.

For a skew k-circulant matrix A, its partition can be expressed as follows: if n/2 is odd,

()

and if n/2 is even,the matrix A is of the same form as (2.2).

Define

()

where

()

and I_m is the mth unit matrix.

It can easily get

()

By applying (2.2), (2.4), and (2.6), we have the following.

Lemma 2.3. If A is an n × n k-circulant matrix, then

()

where M = B + rC, N = B − rC.

By applying (2.2)–(2.6), we have the following.

Lemma 2.4. Let A be a skew k-circulant matrix. If n/2 is odd, then

()

where M = B + rC and N = B − rC. If n/2 is even, P⁻¹AP is of the same form as (2.7).

For a Hermitian k-circulant matrix A, its partition can be expressed as follows: if n/2 is odd,

()

and if n/2 is even, the matrix A is of the same form as (2.2).

Define

()

where i is the imaginary unit.

It can easily get

()

By applying (2.2), (2.4), (2.6), (2.9), (2.10), and (2.11), we have the following.

Lemma 2.5. Let A be an n × n Hermitian k-circulant matrix and Q be defined by the relation (2.10). If n/2 is odd, then

()

is an n × n real matrix, where

()

with Re(T) and Im (T) denoting the real and imaginary parts of the matrix T, respectively. If n/2 is even, then P⁻¹AP is of the same form as (2.7).

Definition 2.6. Given a square matrix A, a function f : Ω ∈ ℂ → ℂ is said to be defined on the spectrum σ(A) of A if f and its derivatives of order l − 1 are defined at each element of σ(A). Here, l is the size of the largest Jordan block of A. If p(x) is the interpolating polynomial of all of these values, the function f of A is defined to be f(A): = p(A).

For instance, the square roots of a matrix A whose eigenvalues belong to exactly one Jordan block are functions of A. These are the primary square roots. On the other hand, choices of different branches of the square root for each Jordan block lead to the so-called nonprimary matrix square root functions of A.

In most applications, it is primary square roots that are of interest and simplicity, virtually all the existing theory and available methods are for such square roots [10]; thus, we will concentrate on primary roots in this paper.

Lemma 2.7 (see [10].)Let the nonsingular matrix A ∈ ℂ^n×n have the Jordan canonical form Z⁻¹AZ = J = diag (J₁, J₂, …, J_p), and let s ≤ p be the number of distinct eigenvalues of A. Let

()

where f(x) = x^1/2 and j_k = 1 or 2 denotes the branch of f. Then A has precisely 2^s square roots that are primary functions of A, given by

()

corresponding to all possible choices of j₁, …, j_p, j_k = 1 or 2, subject to the constraint that j_i = j_k whenever λ_i = λ_k.

If s < p, A has nonprimary square roots. They form parametrized families

()

where j_k = 1 or 2, U is an arbitrary nonsingular matrix that commutes with J, and for each j there exist i and k, depending on j, such that λ_i = λ_k while j_i ≠ j_k.

3. Square Roots

In this section we present some new results which characterize the square roots of the circulant matrices.

3.1. Square Roots of k-Circulant Matrices

It is known that the product of two k-circulant matrices is k-circulant, however, whether a k-circulant matrix has square roots which are also k-circulant or not? We have some answers to this question.

Theorem 3.1. Let A ∈ ℂ^n×n be a nonsingular k-circulant matrix and let X² = A, where X are the primary functions of A. Then all square roots X are k-circulant matrices.

Proof. By assumption, X² = A and X = f(A), here f(x) = x^1/2, which is clearly defined on the spectrum of A, including the case that the eigenvalues of the matrix A are complex numbers. From Definition 2.6, we can construct a polynomial p such that p(A) = f(A). Using the fact that the sum and product of two k-circulant matrices are also k-circulant, the polynomial X = p(A) is a k-circulant matrix.

By Lemma 2.7 and Theorem 3.1, we get that any nonsingular k-circulant matrix always has a k-circulant square root.

In fact, if G⁻¹BG = −B, then A = B² implies G⁻¹AG = A. That means k-circulant matrices may have square roots which are skew k-circulant. Although it is unknown whether it is true, if it has a skew k-circulant matrix, we have the following.

Theorem 3.2. Let A ∈ ℂ^n×n be a nonsingular k-circulant matrix. Assume that A has a skew k-circulant square root. (i) If n/2 is even, then each M and N in (2.7) admits a square root, respectively. (ii) If n/2 is odd, then the matrix M and N in (2.7) are similar.

Proof. let Y be a skew k-circulant matrix and Y² = A.

(i) If n/2 is even, by Lemma 2.4, we have . That implies hold simultaneously, that is Y₁ and Y₂ are square roots of M and N, respectively.

(ii) If n/2 is odd, by Lemma 2.4 again, we have .

Note that Y² = A means that Y₁Y₂ = M and Y₂Y₁ = N. Therefore, Y₁ and Y₂ are both nonsingular (due to the nonsingularity of M and N) and . That is to say, M and N in (2.7) are similar.

In general, a nonsingular k-circulant matrix A, besides the k-circulant square roots, possibly has other kinds of square roots (e.g., skew k-circulant square roots), which are nonprimary functions of A. The existence and the families of square roots depend on the spectrums of M and N. The following theorem gives a classification of all the square roots of a nonsingular k-circulant matrix.

Theorem 3.3. Let the nonsingular k-circulant matrix A ∈ ℂ^n×n has s distinct eigenvalues λ_i (i = 1 : s), then A has 2^s k-circulant square roots that are the primary functions of A, given by

()

corresponding to all possible choices of j₁, …, j_p, j_k = 1 or 2, subject to the constraint that j_i = j_k whenever λ_i = λ_k.

If s < n, A has nonprimary square roots. They form parametrized families

()

where j_k = 1 or 2, U is an arbitrary nonsingular matrix that commutes with Λ, and for each j there exist i and k, depending on j, such that λ_i = λ_k while j_i ≠ j_k.

Proof. According to the hypothesis, A has s distinct eigenvalues. Then by Lemma 2.7, A has 2^s square roots which are primary functions of A and take the form (3.1). By Theorem 3.1, the square roots are k-circulant matrices. By Lemma 2.7 again, we get the form (3.2).

Theorem 3.3 shows that the square roots of a nonsingular k-circulant matrix consist of two classes. The first class comprises finitely many primary square roots which are “isolated,” and they are k-circulant matrices. The second class, which may be empty, comprises a finite number of parametrized families of matrices, each family containing infinitely many square roots sharing the same spectrum, and the square roots in this class maybe k-circulant matrices or not.

3.2. Square Roots of Skew k-Circulant Matrices

If A is an n × n nonsingular skew k-circulant matrix, let (λ, x) be an eigenpair of A. From G⁻¹AG = −A we get AG⁻¹x = −λG⁻¹x which means that the eigenvalues of A must appear in ± pairs, and A has a Jordan decomposition of the following form:

()

with

()

where

()

are m_j × m_j matrices such that

, and δ is a forward shift matrix.

Assume that J has s distinct eigenvalues. We have the following result.

Theorem 3.4. Let the nonsingular skew k-circulant matrix A ∈ ℂ^n×n have the Jordan decomposition (3.3), and let s ≤ l be the number of distinct eigenvalues of J. Then A has 4^s square roots, which are primary functions of A, taking the following form:

()

where L is a primary square root of J and

is a primary square root of

, respectively.

If s < l, then A has nonprimary square roots which are of 4^l − 4^s parameterized families in the following form:

()

where U is an arbitrary nonsingular matrix which commutes with

Proof. The proof consists in using Lemma 2.7 again and the fact that A has 2^s distinct eigenvalues and 2^l Jordan blocks.

Let us consider how to compute the primary square roots of a nonsingular skew k-circulant matrix. If n/2 is even, from Lemma 2.4, we can see that skew k-circulant matrices have the same deduced form (2.7). We can use Algorithm 4.2 (in Section 4) in this case. If n/2 is odd, we have that P⁻¹AP takes the form (2.8). Exploiting this form, we have the following theorem.

Theorem 3.5. Let A ∈ ℂ^n×n be a nonsingular skew k-circulant matrix and let n/2 be odd. Assume that Z ∈ ℂ^n×n and are partitioned as follows:

()

which are conformable with the partition of A in (2.3). Then

is a square root of A if and only if

(A)
Z₂Z₃ is a square root of −(1/4)MN;
(B)
Z₁ is a fourth root of −(1/4)MN;
(C)
Z₄ is a fourth root of −(1/4)NM;
(D)
Z₂ is a solution of Z₁Z₂ + Z₂Z₄ = M.
(E)
Z₃ = M⁻¹Z₂N.

hold simultaneously, where P and M, N are defined by the relation (2.4) and (2.8), respectively.

Proof. The proof is similar to that of Theorem 3.5; see [14].

3.3. Square Roots of Hermitian k-Circulant Matrices

In fact, if , then A = B² implies . That means Hermitian k-circulant matrices may have square roots which are still Hermitian k-circulant. Although it is unknown whether it is true, if it has a Hermitian k-circulant square root, we have the following.

Theorem 3.6. Let A be a nonsingular Hermitian k-circulant matrix, assume that A has a Hermitian k-circulant square matrix. (i) If n/2 is even, then each M and N in (2.7) admits a square root, respectively. (ii) If n/2 is odd, then A’s reduced form R_A ∈ ℝ^n×n in (2.12) has a real square root.

Proof. (i) If n/2 is even, the case is similar to Theorem 3.2.

(ii) If n/2 is odd, let Y be a Hermitian k-circulant matrix and Y² = A. Then, by Lemma 2.5, we have that R_Y = Q⁻¹YQ and R_A = Q⁻¹AQ are real and , where Q is defined in (2.10). This means that R_A has a real square root.

In the following, we give a classification of the square roots of a nonsingular Hermitian k-circulant matrix A. Assume that A is a nonsingular Hermitian k-circulant matrix, λ is an eigenvalue of A, and x is a eigenvector corresponding to λ, that is, Ax = λx. Because

, we have that

, which means the complex eigenvalues of A must appear in conjugate pairs, and A has a Jordan decomposition of the following form:

()

with

()

where J_k is the real Jordan block corresponding to real eigenvalues λ_k for k = 1, …, l;

is the Jordan block corresponding to complex eigenvalues λ_l+k, k = 1, …, r.

Theorem 3.7. Let the nonsingular Hermitian k-circulant matrix A ∈ ℂ^n×n have the Jordan decomposition (3.9). Assume that s ≤ l be the number of distinct real eigenvalues of J_R, and t ≤ r be the number of distinct complex conjugate eigenvalue pairs.

If s ≤ l or t ≤ r, then A has 2^s+2t square roots which are primary functions of A.

If s + t < l + r, then A has square roots which are nonprimary functions of A; they form 2^l+2r − 2^s+2t parameterized families.

Proof. The proof is similar to that of Theorem 3.4.

It is showed in Theorem 3.1 that all the primary square roots of a nonsingular k-circulant matrix A are k-circulant. But for nonsingular Hermitian k-circulant matrices, this conclusion does not hold anymore in general. However, if a square root of a nonsingular Hermitian k-circulant matrix A is a real coefficient polynomial in A, then this conclusion holds.

Theorem 3.8. Let A be a nonsingular Hermitian k-circulant matrix, then all square roots of A which are polynomials in A with real coefficients (if exist) are Hermitian k-circulant matrices.

Proof. Using the fact that the sum and product of two Hermitian k-circulant matrices are also Hermitian k-circulant, we complete the proof.

4. Algorithms

In this section we will propose algorithms for computing the primary square roots of the circulant matrix A in Section 3, which are primary functions of A.

Algorithm 4.1. Computes a primary square root of a nonsingular k-circulant matrix A ∈ ℂ^n×n.

Step 1. Compute the eigenvalues of A.

Step 2. Compute the square roots .

Step 3. Compute , .

Then, we obtain .

The cost of Step 1 is about O(nlog ₂n) flops by discrete Fourier transform. The cost of Step 2 is O(n). The cost of Step 3 is about O(nlog ₂n) flops by inverse discrete Fourier transform. So, it needs about O(nlog ₂n) flops in total if we use the fast Fourier transform to compute a primary square root of a k-circulant matrix A (see Table 1).

Table 1. Flops of Algorithm 4.1.

Step	Flops
1	O(nlog₂n)
2	O(n)
3	O(nlog₂n)

Sum	O(nlog₂n)

Algorithm 4.2. Computes a primary square root of a nonsingular skew k-circulant matrix A ∈ ℂ^n×n (n/2 is even).

Step 1. Compute the reduced form P⁻¹AP = diag (M, N) in (2.7).

Step 2. Compute the Schur decompositions and , respectively, where T_M and T_N are two upper triangular matrices.

Step 3. Compute the upper triangular square roots S_M = f(T_M) and S_N = f(T_N), where T_M has n/2 distinct eigenvalues and so does T_N, here f = λ^1/2 is defined on λ ∈ σ(diag (T_M, T_N)).

Step 4. Compute and .

Step 5. Obtain X = Pdiag (X_M, X_N)P⁻¹.

The costs of Steps 1 and 5 in Algorithm 4.2 are about O(n²) flops. The main costs arise in the implementation of Steps 2–4. Those are about 7(1/12)n³ flops (see Table 2). It needs about 28(1/3)n³ flops in total if we use the Schur method (Algorithm 6.3 in [10]) to compute a primary square root of A directly, that means Algorithm 4.2 is about four times cheaper than the standard Schur method.

Table 2. Flops of Algorithm 4.2.

Step	Flops
1	O(n²)
2	(25/4)n³ + O(n²)
3	(1/12)n³ + O(n²)
4	(3/4)n³ + O(n²)
5	O(n²)

Sum	7(1/12)n³ + O(n²)

Algorithm 4.3. Computes a primary square root of a nonsingular skew k-circulant matrix A ∈ ℂ^n×n (n/2 is odd).

Step 1. Compute the reduced form in (2.8).

Step 2. Compute the Schur decomposition T = U^H(−(1/4)MN)U, where T is upper triangular.

Step 3. Compute the upper triangular fourth root S = f(T), where f = λ^1/4 is defined on λ(T), then compute Z₁ = USU^H.

Step 4. Solve the Sylvester equation .

Step 5. Compute .

Step 6. Compute and .

Step 7. Compute Z₄ = M⁻¹Z₁M.

Step 8. Form Z according to (3.8).

Step 9. Obtain X = PZP⁻¹.

The costs of Steps 1 and 9 in Algorithm 4.3 are about O(n²) flops. The main costs are to implement Steps 2–8. In Step 2, it takes about (1/4)n³ flops for computing matrix-matrix multiplication and 3(1/8)n³ for computing the Schur decomposition of −(1/4)MN. In Step 3, it takes about (1/12)n³ flops to compute the upper triangular fourth root S = f(T) (use Step 3 in Algorithm 4.2 twice) and (3/8)n³ to form Z₁. The cost of Step 4 amounts to about (1/4)n³ flops, see Bartels-Stewart Algorithm in [17]. In Steps 5 and 6, it needs to compute 4 matrix-matrix multiplications, which requires about n³ flops. Step 7 involves a matrix-matrix multiplication and a solution of a linear system of equations with multiple right-hand sides, which needs about (7/12)n³ flops. Thus, the whole sum is about 5(2/3)n³ flops (see Table 3), which means Algorithm 4.3 is about 5 times cheaper than the standard Schur method.

Table 3. Flops of Algorithm 4.3.

Step	Flops
1	O(n²)
2	3(3/8)n³ + O(n²)
3	(11/24)n³ + O(n²)
4	(1/4)n³ + O(n²)
5	(1/2)n³ + O(n²)
6	(1/2)n³ + O(n²)
7	(7/12)n³ + O(n²)
8
9	O(n²)

Sum	5(2/3)n³ + O(n²)

Let n/2 be odd (when n/2 is even, we can use Algorithm 4.2 to compute a primary square root of a nonsingular Hermitian k-circulant matrix).

Algorithm 4.4. Computes a primary square root of a nonsingular Hermitian k-circulant matrix A ∈ ℂ^n×n.

Step 1. Compute the reduced form R_A = Q⁻¹AQ in (2.12).

Step 2. Compute the real Schur decomposition T = V^TR_AV, where T is a upper quasitriangular matrix.

Step 3. Compute S = f(T) (see [8] for more details), where T is upper quasitriangular with distinct eigenvalues and f = λ^1/2 is defined on λ(T).

Step 4. Compute .

Step 5. Compute .

The costs of Steps 1 and 5 in Algorithm 4.4 are about O(n²) flops. The main costs are to implement Steps 2–4. In Step 2, it takes about 25n³ real flops for computing the real Schur decomposition of R_A. In Step 3, it takes about (1/3)n³ real flops for S. The cost of Step 4 amounts to about 3n³ to form . Thus, the whole sum is about 28(1/3)n³ real flops (see Table 4). Note the fact that a complex addition is equivalent to two real additions and a complex multiplication is equivalent to four real multiplications and plus two real additions. So Algorithm 4.4 is approximately eight times cheaper than the standard Schur method.

Table 4. Real flops of Algorithm 4.4.

Step	Flops
1	O(n²)
2	25n³ + O(n²)
3	(1/3)n³ + O(n²)
4	3n³ + O(n²)
5	O(n²)

Sum	28(1/3)n³ + O(n²)

5. Numerical Experiments

We present numerical experiments for the comparison of the algorithms presented in this paper and the standard Schur method with respect to execution time.

All of our computations have been done using MATLAB 7.6.0(R2008a) with unit roundoff u = 2⁻⁵³ ≈ 1.1 × 10⁻¹⁶ and executed in an Intel Pentium M Processor 740, 1.73 GHz with 1 GB of RAM.

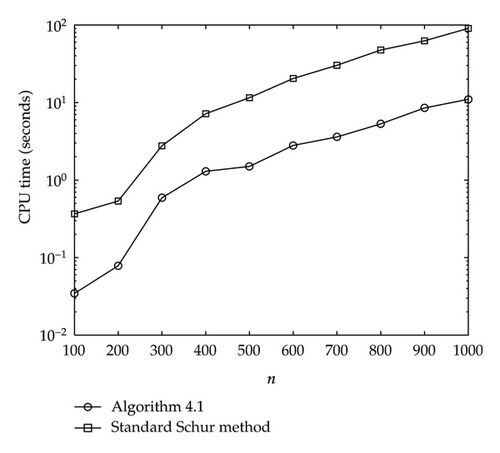
The execution (CPU) time for square roots with respect to n (order of matrix) for Algorithm 4.1 and the standard Schur method is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

CPU time for Algorithm 4.1 and the standard Schur method in logarithmic scale.

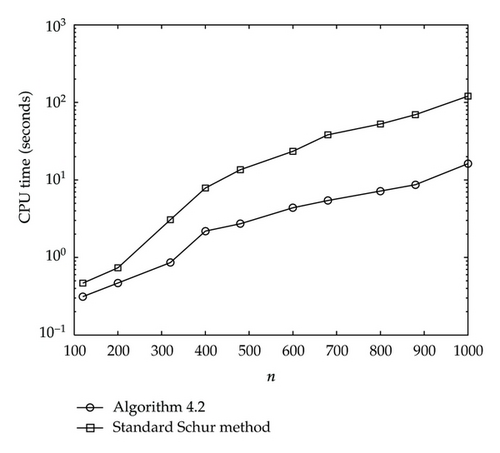
The execution (CPU) time for square roots with respect to n for Algorithm 4.2 and the standard Schur method is shown in Figure 2.

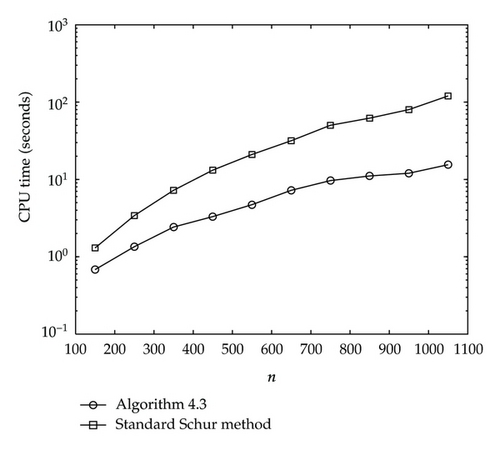
The execution (CPU) time for square roots with respect to n for Algorithm 4.3 and the standard Schur method is shown in Figure 3.

The execution (CPU) time for square roots with respect to n for Algorithm 4.4 and the standard Schur method is shown in Figure 4.

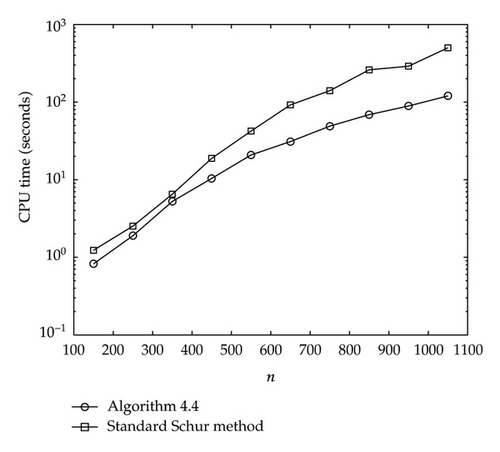
It is evident by the statements of Figures 1–4, the algorithms are clearly faster than the standard Schur methods for computing the circulant matrices in this paper.

Acknowledgments

The author would like to thank the editor and the referees for their helpful comments and valuable suggestions for improving this paper. A Project Supported by Scientific Research Fund of Zhejiang Provincial Education Department (No. Y201223607).

References

1 Davis P. J., Circulant Matrices, 1994, 2nd edition, Chelsea Publishing, New York, NY, USA.
Google Scholar
2 Gray R. M., Toeplitz and Circulant Matrices: A Review, 2000, Stanford University Press, Stanford, Calif, USA.
Google Scholar
3 Mayer A., Castiaux A., and Vigneron J.-P., Electronic Green scattering with n-fold symmetry axis from block circulant matrices, Computer Physics Communications. (1998) 109, no. 1, 81–89, https://doi.org/10.1016/S0010%2D4655(97)00141%2D0, 1621898.
10.1016/S0010-4655(97)00141-0
CAS Web of Science® Google Scholar
4 Cline R. E., Plemmons R. J., and Worm G., Generalized inverses of certain Toeplitz matrices, Linear Algebra and its Applications. (1974) 8, 25–33, 0347844, ZBL0273.15004.
10.1016/0024-3795(74)90004-4
Google Scholar
5 Argiroffo G. R. and Bianchi S. M., On the set covering polyhedron of circulant matrices, Discrete Optimization. (2009) 6, no. 2, 162–173, https://doi.org/10.1016/j.disopt.2008.11.001, 2493319, ZBL1203.90127.
10.1016/j.disopt.2008.11.001
Web of Science® Google Scholar
6 Tsitsas N. L., Alivizatos E. G., and Kalogeropoulos G. H., A recursive algorithm for the inversion of matrices with circulant blocks, Applied Mathematics and Computation. (2007) 188, no. 1, 877–894, https://doi.org/10.1016/j.amc.2006.10.044, 2327764, ZBL1125.65026.
10.1016/j.amc.2006.10.044
Web of Science® Google Scholar
7 Shen S. and Cen J., On the bounds for the norms of r-circulant matrices with the Fibonacci and Lucas numbers, Applied Mathematics and Computation. (2010) 216, no. 10, 2891–2897, https://doi.org/10.1016/j.amc.2010.03.140, 2653105.
10.1016/j.amc.2010.03.140
Web of Science® Google Scholar
8 Jiang Z. L. and Xu Z. B., A new algorithm for computing the inverse and generalized inverse of the scaled factor circulant matrix, Journal of Computational Mathematics. (2008) 26, no. 1, 112–122, 2378589, ZBL1174.65016.
Web of Science® Google Scholar
9 Zhang S. G., Jiang Z. L., and Liu S. Y., An application of the Gröbner basis in computation for the minimal polynomials and inverses of block circulant matrices, Linear Algebra and its Applications. (2002) 347, 101–114, https://doi.org/10.1016/S0024%2D3795(01)00529%2D8, 1899884, ZBL1005.65040.
10.1016/S0024-3795(01)00529-8
Web of Science® Google Scholar
10 Higham N. J., Functions of Matrices: Theory and Computation, 2008, Society for Industrial and Applied Mathematics, Philadelphia, Pa, USA, https://doi.org/10.1137/1.9780898717778, 2396439.
10.1137/1.9780898717778
Web of Science® Google Scholar
11 Cross G. W. and Lancaster P., Square roots of complex matrices, Linear and Multilinear Algebra. (1974) 1, 289–293, 0340278.
10.1080/03081087408817029
Google Scholar
12 Johnson C. R., Okubo K., and Reams R., Uniqueness of matrix square roots and an application, Linear Algebra and its Applications. (2001) 323, no. 1–3, 51–60, https://doi.org/10.1016/S0024%2D3795(00)00243%2D3, 1809757, ZBL0976.15009.
10.1016/S0024-3795(00)00243-3
Web of Science® Google Scholar
13 Hasan M. A., A power method for computing square roots of complex matrices, Journal of Mathematical Analysis and Applications. (1997) 213, no. 2, 393–405, https://doi.org/10.1006/jmaa.1997.5517, 1470859, ZBL0893.65028.
10.1006/jmaa.1997.5517
Web of Science® Google Scholar
14 Lu C. B. and Gu C. Q., The computation of the square roots of circulant matrices, Applied Mathematics and Computation. (2011) 217, no. 16, 6819–6829, https://doi.org/10.1016/j.amc.2011.01.018, 2775673, ZBL1229.65068.
10.1016/j.amc.2011.01.018
Web of Science® Google Scholar
15 Ikramov K. D., Hamiltonian square roots of skew-Hamiltonian matrices revisited, Linear Algebra and its Applications. (2001) 325, no. 1–3, 101–107, https://doi.org/10.1016/S0024%2D3795(00)00304%2D9, 1810098, ZBL0978.15010.
10.1016/S0024-3795(00)00304-9
Web of Science® Google Scholar
16 Reams R., Hadamard inverses, square roots and products of almost semidefinite matrices, Linear Algebra and its Applications. (1999) 288, no. 1–3, 35–43, https://doi.org/10.1016/S0024%2D3795(98)10162%2D3, 1670582, ZBL0933.15006.
10.1016/S0024-3795(98)10162-3
Web of Science® Google Scholar
17 Golub G. H. and van Loan C. F., Matrix Computations, 1996, 3rd edition, Johns Hopkins University Press, Baltimore, Md, USA, 1417720.
CAS Web of Science® Google Scholar

Citing Literature

All articles

Computing the Square Roots of a Class of Circulant Matrices

Abstract

1. Introduction

2. Preliminaries

3. Square Roots

3.1. Square Roots of k-Circulant Matrices

3.2. Square Roots of Skew k-Circulant Matrices

3.3. Square Roots of Hermitian k-Circulant Matrices

4. Algorithms

5. Numerical Experiments

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Computing the Square Roots of a Class of Circulant Matrices

Abstract

1. Introduction

2. Preliminaries

3. Square Roots

3.1. Square Roots of k-Circulant Matrices

3.2. Square Roots of Skew k-Circulant Matrices

3.3. Square Roots of Hermitian k-Circulant Matrices

4. Algorithms

5. Numerical Experiments

Acknowledgments

References

Citing Literature

Figures

References

Related

Information