This paper addresses the problem of finite-time H_∞ filtering for one family of singular stochastic systems with parametric uncertainties and time-varying norm-bounded disturbance. Initially, the definitions of singular stochastic finite-time boundedness and singular stochastic H_∞ finite-time boundedness are presented. Then, the H_∞ filtering is designed for the class of singular stochastic systems with or without uncertain parameters to ensure singular stochastic finite-time boundedness of the filtering error system and satisfy a prescribed H_∞ performance level in some given finite-time interval. Furthermore, sufficient criteria are presented for the solvability of the filtering problems by employing the linear matrix inequality technique. Finally, numerical examples are given to illustrate the validity of the proposed methodology.

1. Introduction

Singular systems also referred to as descriptor systems or generalized state-space systems represent one family of dynamical systems since it generalizes the linear system model and has extensive applications in economics systems, power systems, mechanics systems, chemical processes, and so on; see for more practical examples [1, 2] and the references therein. Many control results in state-space systems have been extended to singular systems, such as stability, stabilization, H_∞ control, and the filtering problems, for instance, see [3–6] and the references therein. Meanwhile, Markovian jump systems are referred to as one special family of hybrid systems and stochastic systems, which are very appropriate to model plants whose structure is subject to random abrupt changes, see the reference [7]. Thus, many attracting results have been studied, such as stochastic stability and stabilization [8, 9], robust control [10–12], guaranteed cost control [13], and other issues. For more details, the readers may be refered to [7, 14] and the references therein. Recently, the problem of state estimation for singular Markovian jump systems has also attracted considerable attention. As far as we know, the traditional Kalman filtering requires the exact knowledge of statistics of the noise signals. To overcome the limitations regarding the system uncertainties and the statistical properties, the H_∞ filtering problem has been proposed and tackled for both the continuous-time case and the discrete-time one including without or with time-delay and full-order or reduced-order [15–20]. For more details, we refer the readers to [7, 21] and the references therein.

On the other hand, in many practical processes, many concerned problems are the practical ones which described that system state does not exceed some bound during some time interval. Compared with classical Lyapunov asymptotical stability, in order to deal with the transient performance of control systems, finite-time stability or short-time stability was introduced in [22]. Employing linear matrix inequality (LMI) theory and Lyapunov function approach, some appealing results were obtained to ensure finite-time stability, finite-time boundedness, and finite-time stabilization of various systems including linear systems, nonlinear systems, and stochastic systems. For instance, Amato et al. [23] investigated the output feedback finite-time stabilization for continuous linear system. Zhang and An [24] considered finite-time control problems for linear stochastic system. For more details of the literature related to finite-time stability, the reader is referred to [25–34] and the references therein. However, to date and to the best of our knowledge, the H_∞ filtering problem for singular stochastic systems has not investigated in finite-time interval. The problem is important and challenging in many practice applications, which motivates us for this study.

This paper deals with the problem of finite-time H_∞ filtering for one family of singular stochastic systems with parametric uncertainties and time-varying norm-bounded disturbance. Our results are totally different from those previous results, although some studies on H_∞ filtering and finite-time stability for singular stochastic systems have been addressed, see [19–21, 31, 32, 35]. The main aim of this paper is to design an H_∞ filtering which guarantees the filtering error system singular stochastic finite-time boundedness and satisfies a prescribed H_∞ performance level in the given finite-time interval. Sufficient criteria are presented for the solvability of the filtering problems by applying the LMI technique. Finally, simulation examples are presented to demonstrate the validity of the developed theoretical results.

Notations. Throughout the paper, ℝⁿ and ℝ^n×m denote the sets of n component real vectors and n × m real matrices, respectively. The superscript T stands for matrix transposition or vector. 𝔼{·} denotes the expectation operator with respective to some probability measure ℙ. In addition, the symbol * denotes the term that is induced by symmetry and diag {⋯} stands for a block-diagonal matrix. λ_min(P) and λ_max(P) denote the smallest and the largest eigenvalue of matrix P, respectively. Notations sup . and inf . denote the supremum and infimum, respectively. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.

2. Problem Formulation

In this paper, let us consider the dynamics of continuous-time singular system with Markovian jumps:

()

where x(t) ∈ ℝⁿ is the state variable,

is the measurement output of the system,

is the signal to be estimated, and E is a singular matrix with rank (E) = r < n; {r_t, t ≥ 0} is continuous-time Markov stochastic process taking values in a finite space 𝕄 : = {1,2, …, N} with transition matrix Γ = (π_ij) _N×N, and the transition probabilities are described as follows:

()

where lim _Δ→0o(Δ)/Δ = 0, π_ij satisfies π_ij ≥ 0 (i ≠ j), and

for all i, j ∈ 𝕄; ΔA(r_t) and ΔB(r_t) are uncertain matrices and satisfy

()

where Δ(r_t) is an unknown, time-varying matrix function and satisfies Δ^T(r_t)Δ(r_t) ≤ I for all r_t ∈ 𝕄; moreover, the disturbance input w(t) ∈ ℝ^p satisfies

()

and the matrices A(r_t), B(r_t), C(r_t), D(r_t), L(r_t), and G(r_t) are coefficient matrices and of appropriate dimension for all r_t ∈ 𝕄.

In this paper, we construct the following full-order filter:

()

where

is the filter state,

is the filter output, and E_f, A_f(r_t), B_f(r_t), and C_f(r_t) are to design the filter matrices with appropriate dimensions.

Define

and combining (2.1) and (2.5), one can obtain the following filtering error dynamics as follows:

()

where

()

For notational simplicity, in the sequel, for each possible r_t = i, i ∈ 𝕄, a matrix K(r_t) will be denoted by K_i; for instance, A(r_t) will be denoted by A_i, B(r_t) by B_i, and so on.

Throughout the paper, we need the following definitions and lemmas.

Definition 2.1 (regular and impulse free, see [21]). (i) The singular system with Markovian jumps (2.1) is said to be regular in time interval [0, T] if the characteristic polynomial det (sE − A_i − ΔA_i) is not identically zero for all t ∈ [0, T].

(ii) The singular systems with Markovian jumps (2.1) is said to be impulse free in time interval [0, T], if deg (det (sE − A_i − ΔA_i)) = rank (E) for all t ∈ [0, T].

Definition 2.2 (singular stochastic finite-time boundedness (SSFTB)). The singular system with Markovian jumps (2.6) which satisfies (2.4) is said to be SSFTB with respect to , with c₁ < c₂, , if the stochastic system (2.6) is regular and impulse free in time interval [0, T] and satisfies

()

Remark 2.3. SSFTB implies that not only is dynamical mode of the filtering error system finite-time bounded but also whole mode of the one is finite-time bounded since the static mode is regular and impulse free.

Definition 2.4 (singular stochastic H∞ finite-time boundedness (SSH∞FTB)). The singular system with Markovian jumps (2.6) is said to be SSH_∞FTB with respect to , if the singular system with Markovian jumps (2.6) is SSFTB with respect to and under the zero-initial condition, the output error e(t) satisfies the cost constrained function

()

for any nonzero w(t) which satisfies (2.4), where γ is a prescribed positive scalar.

Definition 2.5 (see [9].)Let V(x(t), r_t = i, t > 0) be the stochastic function, define its weak infinitesimal operator L of stochastic process {(x(t), r_t = i), t ≥ 0} by

()

Lemma 2.6 (see [36].)For matrices Y, M, and N of appropriate dimensions, where Y is a symmetric matrix, then

()

holds for all matrix F(t) satisfying F^T(t)F(t) ≤ I for all t ∈ ℝ, if and only if there exists a positive constant ϵ, such that the following inequality:

()

holds.

Lemma 2.7 (see [36].)The linear matrix inequality is equivalent to , where and .

Lemma 2.8. The following items are true.

(i) Assume that rank (E) = r, there exist two orthogonal matrices U and V such that E has the decomposition as

()

where Σ_r = diag {δ₁, δ₁, …, δ_r} with δ_k > 0 for all k = 1,2, …, r. Partition U = [U₁ U₂], V = [V₁ V₂], and 𝒱 = [V₁Σ_r V₂] with EV₂ = 0 and

(ii) If P satisfies

()

then

with U and 𝒱 satisfying (2.13) if and only if

()

with P₁₁ ≥ 0 ∈ ℝ^r×r. In addition, when P is nonsingular, one has P₁₁ > 0 and det (P₂₂) ≠ 0. Furthermore, P satisfying (2.14) can be parameterized as

()

where X = diag {P₁₁, Λ}, Y = [P₂₁ P₂₂], and Λ ∈ ℝ^{(n−r)×(n−r)} is an arbitrary parameter matrix.

(iii) If P is a nonsingular matrix, R and Λ are two symmetric positive definite matrices, P and E satisfy (2.14), X is a diagonal matrix from (2.16), and the following equality holds:

()

Then the symmetric positive definite matrix Q = R^−1/2UXU^TR^−1/2 is a solution of (2.17).

Proof. One only requires to prove that (ii) and (iii) hold. Let

()

Then by (2.13) and (2.14), it follows that condition

if and only if P₁₂ = 0 and P₁₁ ≥ 0 ∈ ℝ^r×r. In addition, when P is nonsingular, it follows that P₁₁ > 0 and det (P₂₂) ≠ 0. Noting that (2.13) and U is an orthogonal matrix, thus we have

()

where X = diag {P₁₁, Λ}, Y = [P₂₁ P₂₂] with a parameter matrix Λ ∈ ℝ^{(n−r)×(n−r)}. Thus (ii) is true.

By (i) and (ii), noticing and P = UXU^TE + U₂Y𝒱^T, we have

()

Thus, Q = R^−1/2UXU^TR^−1/2 is a solution of (2.17). This completes the proof of the lemma.

In the paper, our main objective is to concentrate on designing the filter of system (2.1) which guarantees the resulting filtering error dynamic system (2.6) SSH_∞FTB.

3. Main Results

In this section, firstly we give SSH_∞FTB analysis results of the filtering problem for nominal system (2.1). Then these results will be extended to the uncertain systems. Linear matrix inequality conditions are established to show the nominal system or the uncertain system (2.6) is finite-time boundedness, and the output error e(t) and disturbance w(t) satisfy the constrain condition (2.9).

Lemma 3.1. The filtering error system (2.6) is SSFTB with respect to , if there exists a scalar α ≥ 0, a set of nonsingular matrices with , two sets of symmetric positive definite matrices with , with , and for all i ∈ 𝕄 such that the following inequalities hold:

()

Proof. Firstly, one proves the filtering error system (2.6) is regular and impulse free in time interval [0, T]. By Lemma 2.7 and noting that condition (3.1b), one has

()

Now, we choose two orthogonal matrices

and

such that

has the decomposition as

()

where

with δ_k > 0 for all k = 1,2, …, r. Partition

and

with

and

. Denote

()

Noting that condition (3.1a) and

is a nonsingular matrix, by Lemma 2.8, we have

and

. Pre and postmultiplying by

and

, it can easily obtain

. Therefore

is nonsingular, which implies that system (2.6) is regular and impulse free in time interval [0, T].

Let us consider the quadratic Lyapunov function candidate for system (2.6). Computing LV, the derivative of along the solution of system (2.6), we obtain

()

where

. From (3.1b) and (3.5), we obtain

()

Further, (3.6) can be rewritten as

()

Integrating (3.7) from 0 to t, with t ∈ [0, T], we obtain

()

Noting that α ≥ 0, t ∈ [0, T] and condition (3.1c), we have

()

Taking into account that

()

we obtain

()

Therefore, it follows that condition (3.1d) implies

for all t ∈ [0, T]. This completes the proof of the lemma.

Lemma 3.2. The filtering error system (2.6) is SSH_∞FTB with respect to , if there exists a scalar α ≥ 0, a set of nonsingular matrices with , a set of symmetric positive definite matrices with , and for all i ∈ 𝕄 such that (3.1a), (3.1c) and the following inequalities hold:

()

Proof. Noting that

()

Thus, condition (3.12a) implies that

()

Let

for all i ∈ 𝕄, by Lemma 3.1, conditions (3.1a), (3.1c), (3.12b), and (3.14) guarantee that system (2.6) is SSFTB with respect to

. Therefore, we only need to prove that (2.9) holds. Let

and noting that (3.5) and (3.14), we obtain

()

Then using the similar proof as Lemma 3.1, condition (2.9) can be easily obtained and thus is omitted. Therefore, the proof of the lemma is completed.

Denote , and E_f = E. Using Lemmas 2.7 and 3.2, we obtain the following theorem.

Theorem 3.3. The nominal filtering error system (2.6) is SSH_∞FTB with respect to with , if there exists a scalar α ≥ 0, a set of nonsingular matrices {P_i, i ∈ 𝕄} with P_i ∈ ℝ^n×n, a set of positive definite matrices {Q_1i, i ∈ 𝕄} with Q_1i ∈ ℝ^n×n, three sets of matrices {M_i, i ∈ 𝕄} with M_i ∈ ℝ^n×n, {N_i, i ∈ 𝕄} with , {C_fi, i ∈ 𝕄} with , for all i ∈ 𝕄 such that

()

hold, where

, and

In addition, the desired filter parameters can be chosen by

()

Noting that P_i is nonsingular matrix, by Lemma 2.8, there exist two orthogonal matrices U and V, such that E has the decomposition as

()

where Σ_r = diag {δ₁, δ₂, …, δ_r} with δ_k > 0 for all k = 1,2, …, r. Partition U = [U₁ U₂], V = [V₁ V₂], and 𝒱 = [V₁Σ_r V₂] with EV₂ = 0 and

. Let

, from (3.16a),

is of the following form

, and P_i can be expressed as

()

where X_i = diag {P_11i, Λ_i} and Y_i = [P_21i P_22i] with a parameter matrix Λ_i. If we choose Λ_i being a symmetric positive definite matrix, then X_i is a symmetric positive definite matrix. Furthermore, the symmetric positive definite matrix

is a solution of (3.16c), and P_i satisfies

()

From the above discussion, we have the following theorem.

Theorem 3.4. The nominal filtering error system (2.6) is SSH_∞FTB with respect to with , if there exists a scalar α ≥ 0, a set of positive definite matrices {X_i, i ∈ 𝕄} with X_i ∈ ℝ^n×n, four sets of matrices {Y_i, i ∈ 𝕄} with Y_i ∈ ℝ^(n−r)×n, {M_i, i ∈ 𝕄} with M_i ∈ ℝ^n×n, {N_i, i ∈ 𝕄} with , and {C_fi, i ∈ 𝕄} with , for all i ∈ 𝕄 such that (3.16d) and the following linear matrix inequality

()

hold, where

, P_i = UX_iU^TE + U₂Y_i𝒱^T, X_i and Y_i are from the form (3.19); Moreover, other matrical variables are the same as Theorem 3.3.

By Theorems 3.3 and 3.4 and applying Lemmas 2.6–2.8, one can obtain the results stated as follows.

Theorem 3.5. The uncertain filtering error system (2.6) is SSH_∞FTB with respect to with , if there exists a scalar α ≥ 0, a set of positive definite matrices {X_i, i ∈ 𝕄} with X_i ∈ ℝ^n×n, four sets of matrices {Y_i, i ∈ 𝕄} with Y_i ∈ ℝ^(n−r)×n, {M_i, i ∈ 𝕄} with M_i ∈ ℝ^n×n, {N_i, i ∈ 𝕄} with , {C_fi, i ∈ 𝕄} with , and a set of positive scalars {ϵ_i, i ∈ 𝕄}, for all i ∈ 𝕄 such that (3.16d) and the following linear matrix inequality

()

hold, where

, P_i = UX_iU^TE + U₂Y_i𝒱^T, X_i and Y_i are from the form (3.19); Moreover, other matrical variables are the same as Theorem 3.3.

Remark 3.6. Theorems 3.4 and 3.5 extend the H_∞ filtering problem of singular stochastic systems to the finite-time H_∞ filtering problem of singular stochastic systems. In fact, if we fix α = 0 without condition (3.16d), we can obtain sufficient conditions of the H_∞ filtering of singular stochastic systems.

Let I < Q_1i < ηI, then one can check that condition (3.16d) can be guaranteed by imposing the conditions

()

Remark 3.7. The feasibility of conditions stated in Theorem 3.4 and Theorem 3.5 can be turned into the following LMIs-based feasibility problem with a fixed parameter α, respectively:

()

4. Simulation Examples

In this section, numerical results are given to illustrate the effectiveness of the suggested method.

Example 4.1. Consider a two-mode singular stochastic system (2.1) with uncertain parameters as follows:

(i) Mode #1,

()

(ii) Mode #2,

()

and E = diag {1,1, 0}, D₁ = 0.2, G₁ = 0.3, D₂ = 0.1, G₂ = 0.5, d = 0.6, Δ_i = diag {r₁(i), r₂(i), r₃(i)}, where r_j(i) satisfies |r_j(i)| ≤ 1 for all i = 1,2 and j = 1,2, 3. In addition, the switching between the two modes is described by the transition rate matrix

Then, we choose R₁ = R₂ = I₃, T = 2, by Theorem 3.5, the optimal bound with minimum value of relies on the parameter α. We can find feasible solution when 0.34 ≤ α ≤ 11.02. Figures 1 and 2 show the optimal values with different value of α. Noting that when α = 2, it yields the optimal values γ = 9.4643 and c₂ = 5.6786. Then, by using the program fminsearch in the optimization toolbox of Matlab starting at α = 2, the locally convergent solution can be derived as

()

with α = 1.3209, and the optimal values γ = 8.1261, c₂ = 4.8758.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The local optimal bound of γ.

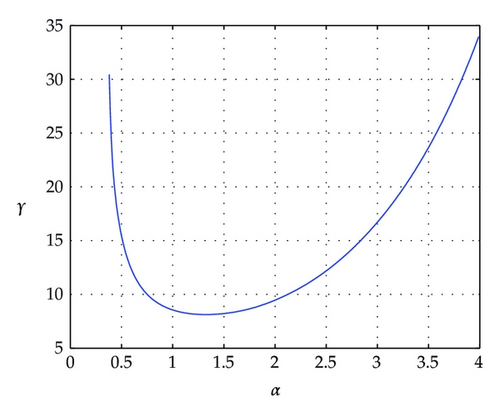
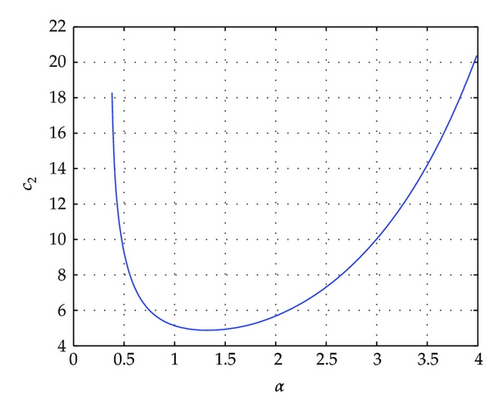
Remark 4.2. From the above example and Remark 3.7, condition (3.22) in Theorem 3.5 is not strict in LMI form, however, one can find the parameter α by an unconstrained nonlinear optimization approach, which a locally convergent solution can be obtained by using the program fminsearch in the optimization toolbox of Matlab.

Example 4.3. Consider a two-mode singular stochastic system (2.1) with uncertain parameters as follows:

()

Moreover, other matrical variables and the transition rate matrix are defined similarly as Example 4.1.

Let R₁ = R₂ = I₃, then the feasible solution of the above filtering error system can be found when α = 0, Theorem 3.5 yields the optimal values γ = 3.7770, c₂ = 2.2663, and

()

Thus, the above filtering error system is stochastically stable and the calculated minimum H_∞ performance γ satisfies ∥T_wz∥<3.7770.

5. Conclusion

In this paper, we deal with the problem of finite-time H_∞ filtering for a class of singular stochastic systems with parametric uncertainties and time-varying norm-bounded disturbance. Designed algorithms are provided to guarantee the filtering error system SSFTB and satisfy a prescribed H_∞ performance level in a given finite-time interval, which can be reduced to feasibility problems involving restricted linear matrix equalities with a fixed parameter. Numerical examples are given to demonstrate the validity of the proposed methodology.

Acknowledgments

The authors would like to thank the reviewers and the editors for their very helpful comments and suggestions to improve the presentation of the paper. The paper was supported by the National Natural Science Foundation of P.R. China under Grant 60874006, by the Doctoral Foundation of Henan University of Technology under Grant 2009BS048, by the Natural Science Foundation of Henan Province of China under Grant 102300410118, by the Foundation of Henan Educational Committee under Grant 2011A120003 and 2011B110009, and by the Foundation of Henan University of Technology under Grant 09XJC011.

References

1 Dai L., Singular Control Systems, 1989, 118, Springer, Berlin, Germany, Lecture Notes in Control and Information Sciences, 986970, https://doi.org/10.1007/BFb0002475, ZBL1002.65518.
10.1007/BFb0002475
Web of Science® Google Scholar
2 Lewis F. L., A survey of linear singular systems, Circuits, Systems, and Signal Processing. (1986) 5, no. 1, 3–36, 893725, https://doi.org/10.1007/BF01600184, ZBL0613.93029.
10.1007/BF01600184
Web of Science® Google Scholar
3 Ishihara J. Y. and Terra M. H., On the Lyapunov theorem for singular systems, IEEE Transactions on Automatic Control. (2002) 47, no. 11, 1926–1930, 1937711, https://doi.org/10.1109/TAC.2002.804463.
10.1109/TAC.2002.804463
Web of Science® Google Scholar
4 Masubuchi I., Kamitane Y., Ohara A., and Suda N., H_∞ control for descriptor systems: a matrix inequalities approach, Automatica. (1997) 33, no. 4, 669–673, https://doi.org/10.1016/S0005%2D1098(96)00193%2D8, 1448959, ZBL0881.93024.
10.1016/S0005-1098(96)00193-8
Web of Science® Google Scholar
5 Xia Y., Shi P., Liu G., and Rees D., Robust mixed H_∞ state-feedback control for continuous-time descriptor systems with parameter uncertainties, Circuits, Systems, and Signal Processing. (2005) 24, no. 4, 431–443, https://doi.org/10.1007/s00034%2D004%2D0917%2D2, 2170596, ZBL1136.93338.
10.1007/s00034-004-0917-2
Web of Science® Google Scholar
6 Zhang L., Huang B., and [email protected], Lam J., LMI synthesis of H₂ and mixed H₂/H_∞ controllers for singular systems, IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing. (2003) 50, no. 9, 615–626, https://doi.org/10.1109/TCSII.2003.816904.
10.1109/TCSII.2003.816904
Web of Science® Google Scholar
7 Boukas E.-K., Control of Singular Systems with Random Abrupt Changes, 2008, Springer, Berlin, Germany, Communications and Control Engineering Series, 2668116.
Google Scholar
8 Boukas E. K., Stabilization of stochastic singular nonlinear hybrid systems, Nonlinear Analysis. (2006) 64, no. 2, 217–228, https://doi.org/10.1016/j.na.2005.05.066, 2188454, ZBL1090.93048.
10.1016/j.na.2005.05.066
Web of Science® Google Scholar
9 Mao X., Stability of stochastic differential equations with Markovian switching, Stochastic Processes and their Applications. (1999) 79, no. 1, 45–67, 1666831, https://doi.org/10.1016/S0304%2D4149(98)00070%2D2, ZBL0962.60043.
10.1016/S0304-4149(98)00070-2
Web of Science® Google Scholar
10 Shi P., Boukas E.-K., and Agarwal R. K., Control of Markovian jump discrete-time systems with norm bounded uncertainty and unknown delay, IEEE Transactions on Automatic Control. (1999) 44, no. 11, 2139–2144, 1735731, https://doi.org/10.1109/9.802932, ZBL1078.93575.
10.1109/9.802932
Web of Science® Google Scholar
11 Boukas E. K., On robust stability of singular systems with random abrupt changes, Nonlinear Analysis. (2005) 63, no. 3, 301–310, https://doi.org/10.1016/j.na.2005.03.110, 2167723, ZBL1089.34046.
10.1016/j.na.2005.03.110
Web of Science® Google Scholar
12 de Souza C. E., Robust stability and stabilization of uncertain discrete-time Markovian jump linear systems, IEEE Transactions on Automatic Control. (2006) 51, no. 5, 836–841, 2232610, https://doi.org/10.1109/TAC.2006.875012.
10.1109/TAC.2006.875012
Web of Science® Google Scholar
13 Boukas E.-K. and Shi P., Stochastic stability and guaranteed cost control of discrete-time uncertain systems with Markovian jumping parameters, International Journal of Robust and Nonlinear Control. (1998) 8, no. 13, 1155–1167, 1656330, https://doi.org/10.1002/(SICI)1099%2D1239(1998110)8:13<1155::AID%2DRNC380>3.0.CO;2%2DF, ZBL0918.93060.
10.1002/(SICI)1099-1239(1998110)8:13<1155::AID-RNC380>3.0.CO;2-F
Web of Science® Google Scholar
14 Krasovskii N. M. and Lidskii E. A., Analytical design of controllers in systems with random attributes, Automation and Remote Control Remote Control. (1961) 22, 1201–1294.
Google Scholar
15 Elsayed A. and Grimble M. J., A new approach to the H_∞ design of optimal digital linear filters, IMA Journal of Mathematical Control and Information. (1989) 6, no. 2, 233–251, 1003679, https://doi.org/10.1093/imamci/6.2.233, ZBL0678.93063.
10.1093/imamci/6.2.233
Web of Science® Google Scholar
16 Mahmoud M. S., Shi P., and Ismail A., Robust Kalman filtering for discrete-time Markovian jump systems with parameter uncertainty, Journal of Computational and Applied Mathematics. (2004) 169, no. 1, 53–69, 2071260, https://doi.org/10.1016/j.cam.2003.11.002, ZBL1067.93059.
10.1016/j.cam.2003.11.002
Web of Science® Google Scholar
17 de Souza C. E., Trofino A., and Barbosa K. A., Mode-independent H_∞ filters for Markovian jump linear systems, IEEE Transactions Automatic Control. (2006) 51, no. 11, 1837–1841, 2265993, https://doi.org/10.1109/TAC.2006.883060.
10.1109/TAC.2006.883060
Web of Science® Google Scholar
18 Xu S., Chen T., and Lam J., Robust H_∞ filtering for uncertain Markovian jump systems with mode-dependent time delays, IEEE Transactions on Automatic Control. (2003) 48, no. 5, 900–907, 1980605, https://doi.org/10.1109/TAC.2003.811277.
10.1109/TAC.2003.811277
Web of Science® Google Scholar
19 Xu S., Lam J., and Zou Y., H_∞ filtering for singular systems, IEEE Transactions on Automatic Control. (2003) 48, no. 12, 2217–2222, 2027248, https://doi.org/10.1109/TAC.2003.820149.
10.1109/TAC.2003.820149
Web of Science® Google Scholar
20 Xu S. and Lam J., Reduced-order H_∞ filtering for singular systems, Systems & Control Letters. (2007) 56, no. 1, 48–57, 2281481, https://doi.org/10.1016/j.sysconle.2006.07.010, ZBL1120.93321.
10.1016/j.sysconle.2006.07.010
Web of Science® Google Scholar
21 Xu S. and Lam J., Robust Control and Filtering of Singular Systems, 2006, 332, Springer, Berlin, Germany, Lecture Notes in Control and Information Sciences, 2232496.
10.1007/11375753_4
Google Scholar
22 Amato F., [email protected], Ariola M., and [email protected], Dorato P., [email protected], Finite-time control of linear systems subject to parametric uncertainties and disturbances, Automatica. (2001) 37, no. 9, 1459–1463, https://doi.org/10.1016/S0005%2D1098(01)00087%2D5, ZBL0983.93060.
10.1016/S0005-1098(01)00087-5
Web of Science® Google Scholar
23 Amato F., Ariola M., and Cosentino C., Finite-time stabilization via dynamic output feedback, Automatica. (2006) 42, no. 2, 337–342, https://doi.org/10.1016/j.automatica.2005.09.007, 2195173, ZBL1099.93042.
10.1016/j.automatica.2005.09.007
Web of Science® Google Scholar
24 Zhang W. and [email protected], An X., [email protected], Finite-time control of linear stochastic systems, International Journal of Innovative Computing, Information and Control. (2008) 4, no. 3, 689–696.
Web of Science® Google Scholar
25 Yang Y., Li J., and Chen G., Finite-time stability and stabilization of nonlinear stochastic hybrid systems, Journal of Mathematical Analysis and Applications. (2009) 356, no. 1, 338–345, 2524242, https://doi.org/10.1016/j.jmaa.2009.02.046, ZBL1163.93033.
10.1016/j.jmaa.2009.02.046
Web of Science® Google Scholar
26 Meng Q. and Shen Y., Finite-time H_∞ control for linear continuous system with norm-bounded disturbance, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1043–1049, 2468938, https://doi.org/10.1016/j.cnsns.2008.03.010, ZBL1221.93066.
10.1016/j.cnsns.2008.03.010
Web of Science® Google Scholar
27 Garcia G., Tarbouriech S., and Bernussou J., Finite-time stabilization of linear time-varying continuous systems, IEEE Transactions on Automatic Control. (2009) 54, no. 2, 364–369, 2491966, https://doi.org/10.1109/TAC.2008.2008325.
10.1109/TAC.2008.2008325
Web of Science® Google Scholar
28 Ambrosino R., Calabrese F., Cosentino C., and De Tommasi G., Sufficient conditions for finite-time stability of impulsive dynamical systems, IEEE Transactions on Automatic Control. (2009) 54, no. 4, 861–865, 2514824, https://doi.org/10.1109/TAC.2008.2010965.
10.1109/TAC.2008.2010965
Web of Science® Google Scholar
29 Amato F., Ambrosino R., Ariola M., and Cosentino C., Finite-time stability of linear time-varying systems with jumps, Automatica. (2009) 45, no. 5, 1354–1358, https://doi.org/10.1016/j.automatica.2008.12.016, 2531617, ZBL1162.93375.
10.1016/j.automatica.2008.12.016
Web of Science® Google Scholar
30 Amato F., Ariola M., and [email protected], Cosentino C., Finite-time control of discrete-time linear systems: analysis and design conditions, Automatica. (2010) 46, no. 5, 919–924, https://doi.org/10.1016/j.automatica.2010.02.008, ZBL1191.93099.
10.1016/j.automatica.2010.02.008
Web of Science® Google Scholar
31 Zhang Y., Liu C., and Mu X., Robust finite-time H_∞ control of singular stochastic systems via static output feedback, Applied Mathematics and Computation. (2012) 218, no. 9, 5629–5640, https://doi.org/10.1016/j.automatica.2010.02.008.
10.1016/j.amc.2011.11.057
Web of Science® Google Scholar
32 Zhang Y., Liu C., and Mu X., Stochastic finite-time guaranteed cost control of Markovian jumping singular systems, Mathematical Problems in Engineering. (2011) 2011, 20, 431751, https://doi.org/10.1155/2011/431751.
10.1155/2011/431751
Web of Science® Google Scholar
33 He S. and Liu F., Stochastic finite-time boundedness of Markovian jumping neural network with uncertain transition probabilities, Applied Mathematical Modelling. (2011) 35, no. 6, 2631–2638, 2776185, https://doi.org/10.1016/j.apm.2010.11.050, ZBL1219.93143.
10.1016/j.apm.2010.11.050
Web of Science® Google Scholar
34 Zhang Y., Liu C., and Mu X., On stochastic finite-time control of discrete-time fuzzy systems with packet dropout, Discrete Dynamics in Nature and Society. (2012) 2012, 18, 752950, https://doi.org/10.1016/j.apm.2010.11.050.
10.1155/2012/752950
Web of Science® Google Scholar
35 Ma S. and Boukas E. K., Robust H_∞ filtering for uncertain discrete Markov jump singular systems with mode-dependent time delay, IET Control Theory & Applications. (2009) 3, no. 3, 351–361, 2502457, https://doi.org/10.1049/iet%2Dcta:20080091.
10.1049/iet-cta:20080091
Web of Science® Google Scholar
36 Boyd S., Ghaoui L. E., Feron E., and Balakrishnan V., Linear Matrix Inequality in Systems and Control Theory, 1994, SIAM, Philadelphia, Pa, USA.
10.1137/1.9781611970777
Google Scholar

Citing Literature

All articles

Finite-Time H_∞ Filtering for Singular Stochastic Systems

Abstract

1. Introduction

2. Problem Formulation

3. Main Results

4. Simulation Examples

5. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Finite-Time H∞ Filtering for Singular Stochastic Systems

Abstract

1. Introduction

2. Problem Formulation

3. Main Results

4. Simulation Examples

5. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

Finite-Time H_∞ Filtering for Singular Stochastic Systems