For its theoretical interest and strong impact on financial markets, option valuation is considered one of the cornerstones of contemporary mathematical finance. This paper specifically studies the valuation of exotic options with digital payoff and flexible payment plan. By means of the Incomplete Fourier Transform, the pricing problem is solved in order to find integral representations of the upfront price for European call and put options. Several applications in the areas of corporate finance, insurance, and real options are discussed. Finally, a new type of digital derivative named supercash option is introduced and some payment schemes are also presented.

1. Introduction

Digital options, also referred to as binary options, are derivatives contracts whose value derives from the value of the so-called underlying asset (e.g., a financial index or a real estate asset). Digital options were first introduced in the 90s by Rubinstein and Reiner [1] and Turnbull [2], and since then their popularity has grown enormously in the derivatives market. In July 2008 they also reached the Chicago Board Options Exchange (CBOE), where digital option contracts on the S&P 500 Index and on the CBOE Volatility Index are traded. Given the peculiar payoff structure, they are embedded in many financial and insurance products and their valuation is crucial for corporate finance and real option problems as well.

In this paper we investigate the digital options world from a fresh perspective. In fact, in the literature, there are several articles devoted to digital options valuation, including [3–5], but none, as far as the authors know, has tried to solve the pricing problem considered here. Our aim is to recover pricing formulas for a wide variety of European installment derivatives with digital-type and path-independent payoffs. In contrast to the smooth payoff patterns of standard options, digital options have discontinuous payoffs, switched completely one way or the other depending on whether the terminal price of the underlying asset satisfies an exercise condition: if such condition occurs, the option pays out a predetermined amount dependent on the terms of the contract; otherwise, the option expires worthless. Furthermore, we consider that the premium can also be paid in installments over the contract lifetime and that the digital option can be lapsed at any payment date before maturity (for more details on the installment feature, see [6–9]).

The rest of the paper is organized as follows. In Section 2 a free boundary problem for the upfront price function and optimal stopping boundary is solved by the Fourier transform method. A general decomposition formula for European-style options with digital payoff structure and flexible payment plan is also derived. Using this approach, several applications in the areas of corporate finance, insurance, and real options are discussed in Section 3. In Section 4 the conclusions are drawn.

2. Problem Formulation

In the standard Black-Scholes-Merton (BSM) model [10, 11], in which there exists a unique risk-neutral probability measure ℚ such that any discounted price process is a martingale and the price process of the risky asset

follows a geometric Brownian motion

()

where

is a standard Brownian motion, σ > 0 the volatility, and μ = (r − δ) the drift, with r ≥ 0 the risk-free rate and δ ≥ 0 the dividend yield, let us consider the European installment options written on S with maturity date T < ∞, payoff H(S_T), and installment rate L_t = L(t). Let H : ℝ⁺ → [y_H, ∞) be a bounded below and left-continuous (resp., right-continuous) function on ℝ⁺ and that H(S_T) → 0 as S_T → 0 (resp., H(S_T) → 0 as S_T → ∞) for call (resp., put) options. Assume that L : [0, T] → ℝ⁺ is a nonnegative real-valued function of bounded variation on [0, T]. Let

be the initial premium function of the option at the time of purchase t ∈ [0, T], defined on the domain 𝒟 = {(S_t, t) ∈ ℝ⁺ × [0, T]}. Let us denote by A_t = A(t; L_t) and G_t = G(t; L_t), for t ∈ [0, T], the optimal stopping (or free) boundaries of call and put options, respectively, such that the domain 𝒟 is divided into a stopping region 𝒮 and a continuation region 𝒞, that is,

()

In order to ensure that the fundamental constraint

is satisfied in the domain 𝒟, it is necessary to impose the following conditions:

()

since the option is worth more alive than dead only in the continuation region 𝒞, where it is then optimal to continue with the installment payments until the maturity date. The initial premium is given by (2.3) if the asset price starts in the stopping region 𝒮, so we assume that the option is alive at the time t ≥ 0 of entering into the contract.

The initial premium function

and the optimal stopping boundary,

for call options and

for put options, jointly solve a free boundary problem consisting of the inhomogeneous BSM partial differential equation (PDE) in 𝒞, that is,

()

subject to the following final and boundary conditions:

()

The Incomplete Fourier Transform (IFT) is used to solve the problem specified by (2.5)–(2.6) in order to obtain an integral representation of the upfront price for the class of European contingent claims with generic payoff and installment rate.

Using the change of variables S_t = e^x and t = T − τ, we get the transformed function v_τ = v(x, τ) ≡ V(e^x, T − τ; L_t) with the continuation region 𝒞_v defined by

()

where a_τ = a(τ) ≡ A(T − τ; L_t) and g_τ = g(τ) ≡ G(T − τ; L_t), respectively, denote the transformed free boundaries of call and put options. It follows that (2.5) reduces to a PDE with constant coefficients

()

with ρ = (r − δ − (1/2)σ²), l_τ = l(τ) ≡ L(T − τ), h(x) ≡ H(e^x) and the associated initial and boundary conditions given by

()

In order to be able to apply the IFT to solve PDE (2.8) for v(x, τ), we will consider the domain 𝒟_v = {(x, τ) ∈ ℝ × [0, T]} by expressing (2.8) as follows:

()

where ℒ_BSM : = (∂/∂τ) − (1/2)σ²(∂²/∂x²) − ρ(∂/∂x) + r is the BSM differential operator and ℋ(x) the Heaviside step function defined as

()

with the initial and boundary conditions that remain unchanged.

Theorem 2.1. Let v(x, τ) be the solution of the PDE (2.10) satisfying the initial and boundary conditions (2.9). Then, the initial premiums of the European installment call and put options with maturity date T, payoff h(x), and payment plan l(τ) are given, respectively, by:

For call options
()
For put options
()

Furthermore, the optimal stopping boundaries a(τ) and g(τ), respectively, for call and put options, satisfy the following relationships:

()

In Appendix A, it is shown how the free boundary problem defined by (2.9)–(2.10) can be solved with the aid of the IFT. Therefore, to price a European installment option for any given payoff pattern h(x) and payment plan l(τ), (2.14) must be solved using numerical methods to find the optimal stopping boundary. Once this is found, the function v(x, τ) can be evaluated via numerical integration. Existence and uniqueness of the solution to the pricing problem of European installment call and put options, as well as the regularity properties of the free boundary, are proved in [12, 13], respectively.

In order to enhance the mathematical tractability and economical meaning, we give a parametric representation of the European installment option price as function of the current asset price S_t and time to maturity τ. This allows to deal with a wide range of payoff structures and payment schemes.

Theorem 2.2. Let H : ℝ⁺ → [y_H, ∞) be differentiable, except for at most a finite number of points, and let L : [0, T] → ℝ⁺ be piecewise continuous over [0, T]. Then, the initial premium functions C(S_t, τ) and P(S_t, τ) of the European installment call and put options can be expressed, respectively, as

()

with

and

the generalized BSM European call and put option pricing formulas

()

and where

()

are the Discounted Expected Payment Streams (DEPS) of call and put options, respectively. Furthermore, the optimal stopping boundaries a_τ and g_τ are given by

()

Theorem 2.2, whose proof is reported in Appendix B, shows that the European installment option price can be divided into two parts: the value of an associated European option with the same characteristics (underlying asset, maturity, and payoff structure) and the DEPS component, which is the present value of all future installment payments along the optimal stopping boundary.

3. Valuation of Digital Installment Options

Now we consider some applications in order to illustrate the flexibility and generality of Theorem 2.2. They cover the fundamental class of digital-type and path-independent payoffs which form the building blocks for pricing a wide range of European derivative securities. In the subsequent propositions, which share a single proof given in Appendix C, we will provide explicit formulas for the initial premium and free boundary of the option corresponding to a certain digital payoff pattern and with a generic payment plan.

3.1. Cash-or-Nothing Payoff

The simplest option with binary payoff profile is the cash-or-nothing call (resp., put) option which pays off nothing if the underlying asset price S_T ∈ [0, ∞) finishes below (resp., above) the strike price K ≥ 0, or pays out a predetermined constant amount X ≥ 0 if the underlying asset finishes above (resp., below) the strike price. Then, the payoff function H^CoN(S_T) of this option contract is given by

()

where ℋ₀(·) is the unit step function, defined as

()

Proposition 3.1. Let H : ℝ⁺ → [y_H, ∞) be defined by (3.1). Then, the initial premiums C^CoN(S_t, τ) and P^CoN(S_t, τ) of the European cash-or-nothing installment call and put options are given, respectively, by

()

3.1.1. Application: Corporate Finance

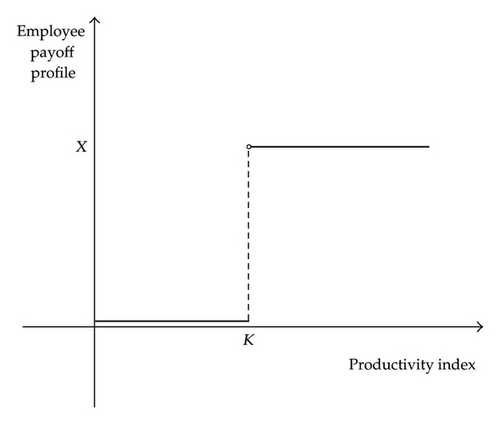
The cash-or-nothing payoff structure is very versatile and apt to represent a wide variety of situations, such as a very interesting corporate finance problem: the executive incentive compensation evaluation. Suppose that a company is considering to introduce an incentive program for its employees such that, if at the end of the year a given productivity index is greater or equal to a contractually specified threshold K, each employee will receive a monetary incentive X. The employee payoff profile as function of the final productivity index is shown in Figure 1. From the company′s perspective, it is very important to set K and X at the “right” level in terms of the cost benefit analysis. In order to perform such research, the valuation of the option given to the employees is crucial and to this extent the analysis here proposed can be very helpful.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Corporate finance: executive incentive compensation.

3.2. Asset-or-Nothing Payoff

The binary asset-or-nothing payoff is characterized by a function H^AoN(S_T) of the form

()

with S_T ∈ [0, ∞) the underlying asset price at maturity T and K ≥ 0 the strike price. From (3.5), we see that an asset-or-nothing call (resp., put) option pays off one unit of the underlying asset if and only if S_T > K (resp., S_T < K), otherwise the payoff is zero.

Proposition 3.2. Let H : ℝ⁺ → [y_H, ∞) be defined by (3.5). Then, the initial premiums C^AoN(S_t, τ) and P^AoN(S_t, τ) of the European asset-or-nothing installment call and put options are given, respectively, by

()

3.2.1. Application: Insurance

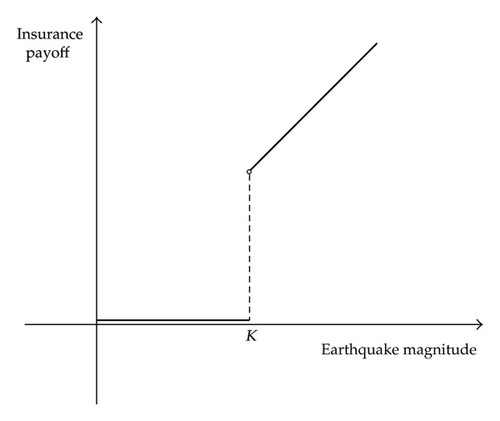
An insurance contract provides protection against loss for which periodically a premium is paid in exchange for a guarantee that there will be a compensation, under stipulated conditions, for a loss caused by a specified event. Given the nature of the risk insured and the payment structure, installment options are very suitable for valuation purposes and asset-or-nothing payoffs in particular are often embedded in insurance products. Let us consider for instance an earthquake insurance that provides a coverage proportional to the earthquake magnitude. Suppose that the insurance is provided only above a certain earthquake magnitude level K and that the resulting payoff grows linearly. The resulting insurance payoff as function of the earthquake magnitude is depicted in Figure 2.

3.3. Gap Payoff

The third derivative built from a digital payoff is the gap option. The payoff function H^G(S_T), for S_T ∈ [0, ∞), of this option contract is defined by

()

that is, the holder of a call (resp., put) option receives nothing if the underlying asset price S_T finishes below (resp., above) the trigger price K ≥ 0, or she gets a payout of S_T − X (resp., X − S_T), with X ≥ 0 the strike price, if and only if S_T > K (resp., S_T < K). The gap payoff reverts to the standard one when trigger and strike prices coincide, that is, K ≡ X. Notice that the trigger price K determines whether or not the option contract will be exercised at expiry, while the strike price X determines the amount of the nonzero payoff, which may be positive or negative depending on the settings of X and K.

Proposition 3.3. Let H : ℝ⁺ → [y_H, ∞) be defined by (3.8). Then, the initial premiums C^G(S_t, τ) and P^G(S_t, τ) of the European gap installment call and put options are given, respectively, by

()

3.3.1. Application: Real Options

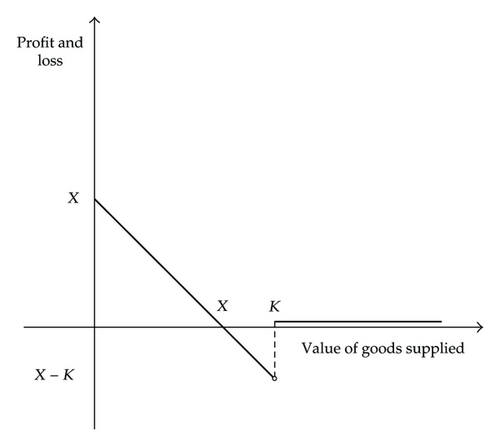
A rather common situation where gap option evaluation is relevant is the following real option case. Let us consider a request for tender by an agency for the supply of a given maximum quantity of goods of value K in exchange of a fixed amount of money X, with 0 < X < K. The quantity of goods supplied is a stochastic variable. It is known only at maturity and matches the demand at that date. Thus, the maximum quantity of goods is chosen by the agency large enough so that the demand does not exceed the level K. The cost of the goods is known, linear and independent from the quantity supplied (i.e., there are no economies of scale). The supplier′s profit and loss as function of the value of the goods supplied is represented in Figure 3. It is interesting to note that if the actual demand exceeds the level X, the supplier will incur in a loss, unlike most options final payoffs.

3.4. Range Binary Payoffs

So far we have considered options with payoffs having only one singularity. Range binary payoffs present two points of discontinuity in a given bounded interval within which must lie the terminal price of the underlying asset so that the option expires in-the-money. This feature makes range binary options cheaper than their plain vanilla counterpart.

Following the original idea in [14], we consider an option with an asset-or-nothing range binary payoff. This option contract, which is referred to as supershare option, entitles its owner to a given monetary unit value proportion of the underlying asset, provided that its price S_T ∈ [0, ∞) finishes within a lower value K_l and an upper value K_u; otherwise, the option expires worthless. Then, the payoff function H^SS(S_T) of a supershare option is defined as follows:

()

where

, with 0 < K_l < K_u.

Proposition 3.4. Let H : ℝ⁺ → [y_H, ∞) be defined by (3.11). Then, the initial premiums C^SS(S_t, τ) and P^SS(S_t, τ) of the European supershare installment call and put options are given, respectively, by

()

We now introduce a new type of option contract that entitles the holder to receive a fixed cash amount X ≥ 0 if the underlying asset price S_T ∈ [0, ∞) lies between a lower limit K_l and an upper limit K_u, and zero otherwise. A cash-or-nothing range binary option, hereafter called supercash call option, has a payoff function H^SC(S_T) of the form

()

that is, the option finishes in-the-money if and only if S_T ∈ (K_l, K_u].

Proposition 3.5. Let H : ℝ⁺ → [y_H, ∞) be defined by (3.14). Then, the initial premium C^SC(S_t, τ) of the European supercash installment call option is given by

()

3.4.1. Application: Structured Products

Range binary options are very attractive for creating structured financial products. In fact their peculiar payoff pattern allows to tailor made contracts meeting the expectations of the potential buyer. More importantly, by doing so it is possible to cut the costs relative to those scenarios that the buyer considers uninteresting. Therefore, the pricing framework of the range binary options is very useful for evaluation purposes in case of setting up investment strategies or when analyzing insurance products which are effective only within a certain range.

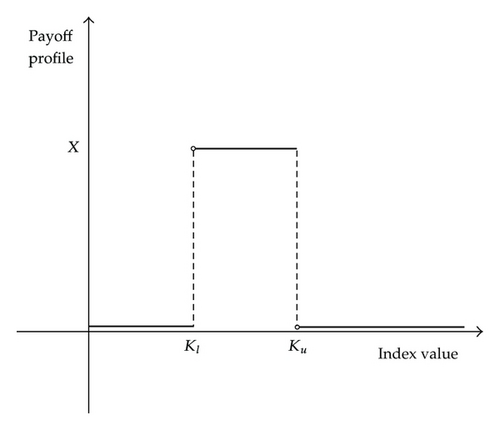
For instance, let us consider at time t ≥ 0 an individual investor who holds a risky portfolio and needs to withdraw a fixed amount of money X > 0 at a prespecified time T > t to meet an obligation. In this case, in order to hedge the market risk, the investor could buy a cash-or-nothing installment put option with maturity date T which pays the constant amount X if an appropriate index that mimics his/her portfolio value is below a certain threshold K. Alternatively, excluding some tail scenarios, he/she could choose a cheaper option, a supercash installment call option, that guarantees the same amount X if at maturity T the index value, as shown in Figure 4, lies within a certain range (K_l, K_u], with K_u = K. Furthermore, the installment feature allows the investor to drop the option as soon as the market conditions turn out to be reasonably favorable.

3.5. Flexible Payment Plans

In this paragraph, we analyze in greater detail the wide class of time-varying payment schemes, specifying two different functional forms of the installment rate L(t) and focusing on the DEPS representation for call options.

Assume an installment payment function L : [0, T] → ℝ⁺ of the form

()

Clearly the condition q₀ < q₁ (resp., q₀ > q₁) leads to a monotonically increasing (resp., decreasing) function of t. It is also straightforward to obtain the constant payment stream by setting q₀ = q₁ ≡ q, with

. Figure 5(a) shows the plot of the installment rate L(t) as a linear function of the time t with a positive (solid line) and negative (dashed line) slope; the special case L(t) ≡ q is represented by the horizontal dotted line. Three possible payment schemes can be outlined in this case: (1) it increases at a constant rate from q₀ at t = 0 to q₁ at t = T; (2) it decreases at a constant rate from q₀ to q₁; (3) it is constant for all times. Then, from (2.19), we get

()

with α₀ = q₁ and α₁ = (q₁ − q₀)/(T).

Finally, the installment rate L(t) is supposed to be a linear combination of characteristic functions of disjoint bounded intervals, that is,

()

where n ∈ ℕ and {I_k = [t_k, t_k+1), k = 0, 1, …, n − 1} is a partition 𝒫 of the time interval [0, T], with 𝒳_I the indicator function defined as

()

The function L : [0, T] → ℝ⁺ defined by (3.18) is called step function and it is continuous from the right: the size of the step at point t_k is |q_k − q_k−1|, for all k = 1, 2, …, n − 1. By definition, L(t) is a piecewise constant function having at most a countable number of steps since it either remains the same or changes value going from one interval to the next. It follows that in this case, the payment scheme can be monotonic or not over time depending on whether {q₀, q₁, …, q_n−1} is a real sequence. Therefore, as shown in Figure 5(b), if, for k = 1, …, n − 1, either condition q_k−1 ≤ q_k or condition q_k−1 ≥ q_k holds, then the installment rate L(t) is either increasing (solid segments) or decreasing (dashed segments) with respect to t; while it reduces to a constant (horizontal dotted line) if and only if, for all k, q_k ≡ q, with

. Note that, when L(t) is strictly monotonic, then it is often referred to as the staircase function. Then, from (2.19), we have

()

where τ_k = t_n − t_n−k is the length of the interval (t_n, t_n−k] and α_k = q_n−(k+1), for k = 0, 1, …, n − 1, are the constant coefficients associated with the partition 𝒫([0, T]).

4. Conclusions

In this paper, we have studied the valuation of exotic options with digital payoff and flexible payment plan. Taking the free boundary problem formulation, we have used the Fourier transform method to solve the inhomogeneous Black-Scholes-Merton equation subject to the appropriate boundary and terminal conditions. An integral representation of the upfront price and its decomposition formula has been proposed.

The class of path-independent options with discontinuous payoffs forms the building blocks for pricing a wide range of securities such as barrier options, structured convertible bonds, and mortgage-backed securities. This framework has been usefully applied to solve problems in different areas, including corporate finance, insurance, and real options.

Appendices

A. Proof of Theorem 2.1

Focusing on call options, we reduce (2.10) to an ordinary differential equation (ODE) by using the auxiliary function y_τ = y(x, τ) : = e^−xv(x, τ), for which the condition lim _x→∞ y(x, τ) = 0 does hold. Writing v_τ and its derivatives in terms of y_τ and substituting into (2.10) yield

()

with θ = (ρ + σ²), m_τ = m(x, τ) : = e^−xl(τ), and where the associated initial and boundary conditions (2.9) are expressed by

()

By applying the definition of the IFT to (A.1), we have

()

where

is the IFT applied to the functions y(x, τ) and m(x, τ) in the continuation region 𝒞_v.

Using the properties of the Fourier transform of the derivatives of y_τ along with the boundary conditions (A.3)-(A.4), the following three identities are obtained

()

and substituting into (A.5) yields

()

where

, and with the initial condition

calculated from (A.2). Using the integrating factor method, we find that the solution for

is given by

()

Applying the inverse Fourier transform ℱ⁻¹, we obtain for the function y(x, τ) the following representation:

()

with

()

To determine explicit expressions for y₁(x, τ) and y₂(x, τ), we will use the Convolution Theorem for Fourier transforms, which, for arbitrary functions f(x, τ₁) and g(x, τ₂), is written as

()

In order to apply this result to the definition of y₁(x, τ), we let

()

and then using the inverse Fourier transform, we get

()

where the last expression is obtained by setting λ₁ = (σ²/2)τ, λ₂ = i[−(x + θτ)], n = 0, and making use of the following identity:

()

in which λ₁ and λ₂ are any complex functions not involving the integration variable ω, with Re(λ₁) ≥ 0 and n ∈ ℕ₀. By rearranging terms of (x+θτ)², the function f(x, τ₁) can be simplified as follows:

()

Letting now

yields

()

Then, substituting for f(x − u, τ₁) and g(u, τ₂) into (A.11), we obtain

()

Next, we consider the definition of y₂(x, τ) which can be written as

()

To evaluate the above integral by the Convolution Theorem, we let

()

then applying the inverse Fourier transform to the functions F(ω, τ₁) and G(ω, τ₂), we get, respectively,

()

where the last expression of f(x, τ₁) is obtained by (A.14) setting λ₁ = (σ²/2)(τ − ξ), λ₂ = i[−(x + θ(τ − ξ))] and n = 0. Hence, it is quite straightforward to express the function f(x, τ₁) as follows:

()

Then, substituting for f(x − u, τ₁) and g(u, τ₂) into (A.11) yields

()

Finally, replacing the expressions for y₁(x, τ) and y₂(x, τ) into (A.9), making use of the Heaviside step function on the continuation region 𝒞_v, and recovering v(x, τ) as e^xy(x, τ), we obtain the integral representation (2.12) defining the initial premium v(x, τ) of the European installment call option.

Similarly, for put options, by expressing PDE (2.10) and (2.9) in terms of the newly defined auxiliary function y(x, τ) : = e^xv(x, τ), we are able to apply the IFT (since the required condition lim _x→−∞ y(x, τ) = 0 is fulfilled) and then obtain the solution for the resulting ODE. Taking the inverse Fourier transform of this solution in conjunction with the Convolution Theorem and then recovering the original function v(x, τ), we derive the integral representation (2.13) for the initial premium v(x, τ) of the European installment put option.

Now, applying the second condition in (2.9), that is, imposing that the function v(x, τ) is equal to zero as x tends to the optimal stopping boundary, we get (2.14) which completes the proof.

B. Proof of Theorem 2.2

Focusing on call options, we consider the first integral in the right-hand side of (2.12), which can be written as follows:

()

with h′(x) = dh(x)/dx. Multiplying and dividing by e^u in the first term of v₁(x, τ) yield

()

Adding and subtracting appropriate terms, we have

()

and substituting it into I₁(x, τ) yields

()

Setting

and defining

, we get

()

Similarly, the second term of v₁(x, τ) can be written as

()

Setting

and defining

, we obtain

()

Furthermore, the second integral in the right-hand side of (2.12) can be simplified as follows:

()

Performing the change of variable

and using the above definition of d₂(·, ·, ·), yields

()

where N(·) is the standard normal cumulative distribution function given by the formula

()

Substituting the expressions of v₁(x, τ) and v₂(x, τ) into (2.12) and reverting back to the original variable via S_t = e^x, we obtain (2.15) in conjunction with the expressions (2.17) and (2.19) defining and Λ^C(S_t, τ; a(·)), respectively. Finally, because the early stopping decision is optimal when S_t = a_τ, by applying the value matching condition (2.14), we get (2.21).

C. Proof of Propositions 3.1–3.5

In this appendix, we consider the European installment call option whose payoff function H : ℝ⁺ → [y_H, ∞) is defined by

()

where ϕ : ℝ⁺ → ℝ is a linear function of the terminal asset price S_T, that is,

()

K_l and K_u, with 0 < K_l < K_u, are, respectively, a lower and an upper limit to the values of S_T for which the option is in-the-money. Performing the change of variable S_T = e^u, the function h(u) ≡ H(e^u) and its first derivative can be written, respectively, as

()

where δ₀(·) is the Dirac delta function, representing the derivative of ℋ₀(·) and defined by the following two properties:

()

From (B.5)–(B.7) in the proof of Theorem 2.2, it follows that

is the sum of two integrals, I₁(·, ·) and I₂(·, ·), as expressed by the general formula (2.17). Substituting the expression for h^′(·) into (B.5) and then rearranging terms yield

()

with

. It is easy to see (e.g., by integration by parts) that the second term vanishes and then, splitting the first one in two parts, the above equation becomes

()

Solving the inequalities

and

for z_u and using the indicator function 1_{x>0} = ℋ₀(x) yield

()

Since it can be shown that

, that is, the optimal stopping boundary at expiry, is equal to the trigger prices K_l and K_u for the first and the second integrals, respectively, the above equation becomes

()

and using the definition of the cumulative distribution function N(·) given in (B.10) yields

()

Plugging the expressions for h(·) and h^′(·) into (B.7), it follows that

()

with

. However, the second term into I₂(x, τ) vanishes and the first one can be split in two parts. Solving the inequalities

and

for ζ_u and using the same arguments as before, we get

()

Going back to S_t = e^x and substituting for I₁(·, ·) and I₂(·, ·) from (C.9) and (C.11) into (2.17) yield

()

Propositions 3.4-3.5 are easily proved using (C.12) since the in-the-money region is the bounded interval (K_l, K_u]. Plugging {(ϕ₀ = 0)∧(ϕ₁ = 1/K_l)} into (C.12), we have the explicit expression for and substituting it into (2.15) yields (3.12). Similarly, setting {(ϕ₀ = X)∧(ϕ₁ = 0)} in (C.12) and substituting the resulting expression into (2.15), we get (3.15).

The proofs of Propositions 3.1–3.3 can be obtained by setting K_l = K and taking the limit of the right-hand side of (C.12) as K_u goes to infinity, that is, using the following result:

()

since the option is in-the-money on the unbounded interval (K, ∞). Equations (3.3) and (3.6) are derived from (2.15) by setting the couple of parameters values {(ϕ₀ = X)∧(ϕ₁ = 0)} and {(ϕ₀ = 0)∧(ϕ₁ = 1), respectively, and plugging it into (C.13). In a similar way, setting {(ϕ₀ = −X)∧(ϕ₁ = 1)} in (C.13) and substituting the expression for

into (2.15) yield (3.9).

References

1 Rubinstein M. and Reiner E., Unscrambling the binary code, Risk. (1991) 4, 75–83.
Google Scholar
2 Turnbull S. M., Interest rate digital options and range notes, Journal of Derivatives. (1995) 3, 92–101, https://doi.org/10.3905/jod.1995.407931.
10.3905/jod.1995.407931
Google Scholar
3 Chriss N. and Ong M., Digitals defused, Risk. (1995) 8, 56–59.
Google Scholar
4 Zhang P. G., Correlation digital options, Journal of Financial Engineering. (1995) 4, 75–96.
Google Scholar
5 Ingersoll J. E., Digital contracts: simple tools for pricing complex derivatives, Journal of Business. (2000) 73, no. 1, 67–88, 2-s2.0-0040777009, https://doi.org/10.1086/209632.
10.1086/209632
Web of Science® Google Scholar
6 Karsenty F. and Sikorav J., Instalment plan, Risk. (1993) 6, 36–40.
Google Scholar
7 Davis M. H. A., Schachermayer W., and Tompkins R. G., Pricing, no-arbitrage bounds and robust hedging of instalment options, Quantitative Finance. (2001) 1, no. 6, 597–610, https://doi.org/10.1088/1469%2D7688/1/6/302, 1870017.
10.1080/713666004
Google Scholar
8 Ben-Ameur H., Breton M., and François P., A dynamic programming approach to price installment options, European Journal of Operational Research. (2006) 169, no. 2, 667–676, https://doi.org/10.1016/j.ejor.2004.05.009, 2172366, ZBL1079.90147.
10.1016/j.ejor.2004.05.009
Web of Science® Google Scholar
9 Kimura T., Valuing continuous-installment options, European Journal of Operational Research. (2010) 201, no. 1, 222–230, https://doi.org/10.1016/j.ejor.2009.02.010, 2573333, ZBL1177.91130.
10.1016/j.ejor.2009.02.010
Web of Science® Google Scholar
10 Black F. and Scholes M., The pricing of options and corporate liabilities, Journal of Political Economy. (1973) 81, 637–654, https://doi.org/10.1086/260062, ZBL1092.91524.
10.1086/260062
Web of Science® Google Scholar
11 Merton R. C., Theory of rational option pricing, Bell Journal of Economics and Management Science. (1973) 4, 141–183, 0496534.
10.2307/3003143
Web of Science® Google Scholar
12 Yi F., Yang Z., and Wang X., A variational inequality arising from European installment call options pricing, SIAM Journal on Mathematical Analysis. (2008) 40, no. 1, 306–326, https://doi.org/10.1137/060670353, 2403323, ZBL1168.35453.
10.1137/060670353
Web of Science® Google Scholar
13 Yang Z. and Yi F., Valuation of European installment put option: variational inequality approach, Communications in Contemporary Mathematics. (2009) 11, no. 2, 279–307, https://doi.org/10.1142/S0219199709003363, 2518582, ZBL1180.35586.
10.1142/S0219199709003363
Web of Science® Google Scholar
14 Hakansson N. H., The purchasing power new found: a new kind of financial intermediary, Financial Analysts Journal. (1976) 32, 49–59, https://doi.org/10.2469/faj.v32.n6.49.
10.2469/faj.v32.n6.49
Google Scholar

All articles

Pricing and Applications of Digital Installment Options

Abstract

1. Introduction

2. Problem Formulation