Cooling Intensification of a Continuously Moving Stretching Surface Using Different Types of Nanofluids
Abstract
The effect of different types of nanoparticles on the heat transfer from a continuously moving stretching surface in a concurrent, parallel free stream has been studied. The stretching surface is assumed to have power-law velocity and temperature. The governing equations are converted into a dimensionless system of equations using nonsimilarity variables. Resulting equations are solved numerically for various values of flow parameters. The effect of physical quantities on the temperature profiles is discussed in detail.
1. Introduction
The thermal management of continuously moving surfaces in a quiescent or flowing fluid plays a major role in determining the quality of final products and production rates during many manufacturing processes such as extrusion of metal or polymer sheets, wire drawing, glass fiber production, continuous casting, and paper production. Since the pioneering work of Sakiadis [1], considerable attention has been given to the flow and heat transfer over a continuously moving surface by many researchers. Elbashbeshy and Bazid [2] investigated the heat transfer over an unsteady stretching surface. This study reveals that the rate of the heat transfer increases with the increase of the unsteadiness parameter and Prandtl number. Tsou et al. [3] obtained analytical and experimental results for the flow and heat transfer over a continuously moving surface. Gupta and Gupta [4] analyzed the heat and mass transfer in the flow over a porous stretching sheet. Chen [5] studied the flow and heat transfer from a heated flat surface continuously moving in a parallel free stream of non-Newtonian fluid and found that the heat transfer rate increases with an increase in the ratio of the free stream velocity to the wall velocity. Devi and Thiyagarajan [6] investigated the hydromagnetic flow and heat transfer over a nonlinearly stretching sheet with variable surface temperature. Hassanien et al. [7] studied the boundary layer solutions for the flow and heat transfer over a continuously flat surface moving in a parallel free stream. Al-Sanea and Ali [8] investigated the effect of extrusion slit on the flow and heat transfer from a continuously moving material with suction or injection. Cortell [9] performed a numerical analysis for the flow and heat transfer in a viscous fluid over a nonlinearly stretching sheet.
It is well known that conventional heat transfer fluids used in the above-mentioned studies have low thermal properties. Rapid developments in modern manufacturing techniques allow for the production of nanosized metallic or nonmetallic particles in the range between 1 and 100 nm which are used as additives inside the base fluids such as water, oil, and ethylene glycol for improving heat transfer. This new type of liquid-solid mixture is termed nanofluid. Starting from studies of Masuda et al. [10] and Choi [11], nanofluids have attracted great interest because of the their unique thermal properties. Wen and Ding [12] observed that the usage of Al2O3 nanoparticles in water significantly enhances the convective heat transfer in the laminar flow region. Santra et al. [13] studied heat transfer of a copper-water nanofluid through two isothermally heated parallel plates and found that the rate of heat transfer increases with the increase in flow as well as the increase in nanoparticle volume fraction. Eastman et al. [14] observed that effective thermal conductivity of ethylene glycol significantly increased for 0.3% volume fraction of Cu nanoparticles. Abu-Nada et al. [15] investigated natural convection heat transfer enhancement in horizontal concentric annuli using different types of nanofluids. Their results indicate that for high values of the Rayleigh number, nanoparticles with high thermal conductivity cause significant enhancement of heat transfer characteristics. On the other hand, for intermediate values of the Rayleigh number, nanoparticles with low thermal conductivity cause a reduction in heat transfer. Hamad and Pop [16] used scaling transformations for boundary layer flow near the stagnation point on a permeable stretching sheet in a porous medium saturated with a nanofluid. Bachok et al. [17] investigated the flow and heat transfer in a viscous fluid near the three-dimensional stagnation point of a body that is placed in a water-based nanofluid containing different types of nanoparticles and found that nanoparticles suspended in a fluid are capable of increasing the heat transfer capability of the base fluids. Vajravelu et al. [18] studied the convective heat transfer in the flow of viscous nanofluids over a stretching sheet. Hady et al. [19] studied the radiation effect on the viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Yacob et al. [20] investigated the steady boundary layer shear flow over a stretching/shrinking sheet in a nanofluid.
The aim of this work is to investigate the effect of different types of nanoparticles (namely, copper (Cu) and Alumina (Al2O3)) on the heat transfer from a continuously moving stretching surface in a concurrent, parallel free stream. The stretching surface is assumed to have power-law velocity and temperature. The governing equations are made dimensionless using nonsimilarity variables. Local nonsimilarity solutions are obtained for the temperature distributions. The results are given in tabular and graphical forms. The effects of the problem parameters are discussed in detail.
2. Formulation of the Problem
The geometry of the present problem and its coordinate system are shown in Figure 1. The stretching surface moves as a two-dimensional sheet and originates from a slot with power-law velocity through the nanofluid medium subjected to the uniform-free stream velocity, U∞.
| Substances | k (W/mK) | ρ (kg/m3) | cp (J/kgK) | Pr |
|---|---|---|---|---|
| Water | 0.613 | 997.1 | 4179 | 6.2 |
| Cu | 401 | 8933 | 385 | — |
| Al2O3 | 40 | 3970 | 765 | — |
In contrast to the local similarity method, the nonsimilar terms on the right-hand side of the boundary layer equations are retained. As a consequence of this, it is expected that the results obtained from the local nonsimilarity method are more accurate than those of the local similarity method. The set of coupled equations (2.10) can be treated as a system of ordinary differential equations with ξ being treated as a constant parameter in any streamwise location.
The primary physical quantity of interest is the local Nusselt number which represents the surface heat transfer rate.
3. Results and Discussions
The transformed local nonsimilar equations (2.10) subject to boundary conditions in (2.11) are solved numerically using the effective shooting technique with a fourth-order Runge-Kutta integration scheme in conjunction with the Newton-Raphson method for systematic guessing of f′(ξ, 0), θ′(ξ, 0), g′(ξ, 0), and h′(ξ, 0). The convergence criterion of the obtained results is of order 10−6. In order to test the accuracy of the present method, local similarity results of the present problem are compared with those of Chen [25] and Soundalgekar and Ramana Murty [26] in Table 2 and a good agreement is found. Heat transfer results obtained only for θ and its derivative which is physically relevant is displayed in graphical and tabular forms for various values of problem parameters to see the developments in the temperature profiles.
| Pr | Soundalgekar and Murty | Chen | Present results | |||
|---|---|---|---|---|---|---|
| m = 0 | m = 1 | m = 0 | m = 1 | m = 0 | m = 1 | |
| 0.7 | 0.3508 | 0.8028 | 0.3509 | 0.8029 | 0.3508 | 0.8028 |
| 2 | 0.6831 | 1.4683 | 0.6832 | 1.4683 | 0.6833 | 1.4683 |
| 10 | 1.6808 | 3.4515 | 1.6802 | 3.4517 | 1.6803 | 3.4516 |
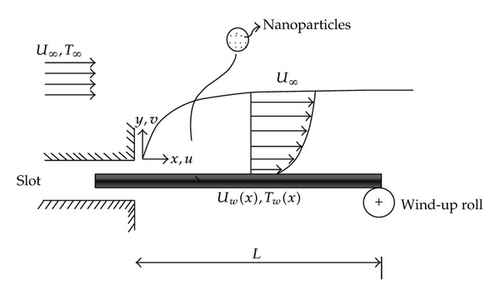
Figure 2 is constructed to demonstrate the effect of the volume fraction ψ on the temperature profiles. It is clear that thermal boundary layer thickness increases as ψ increases. Physically, if the nanoparticle volume fraction increases, the thermal diffusivity of the nanofluid increases and this phenomenon leads to the faster propagation of heat into the nanofluid which increases the thermal boundary layer thickness. It is also observed that this effect is more pronounced for alumina nanofluids.
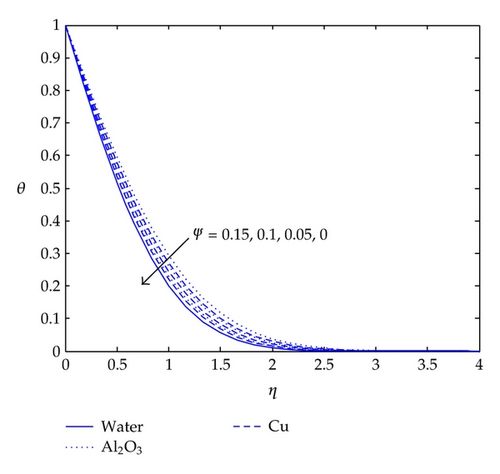
Figure 3 displays temperature profiles for different values of the surface temperature distribution exponent m. It is obvious that the temperature at a point decreases with an increase in m. In addition, the adiabatic wall condition is achieved for m = −0.5; when m > −0.5, heat flows from the stretching surface into the nanofluid medium and a negative temperature gradient is observed at the surface.
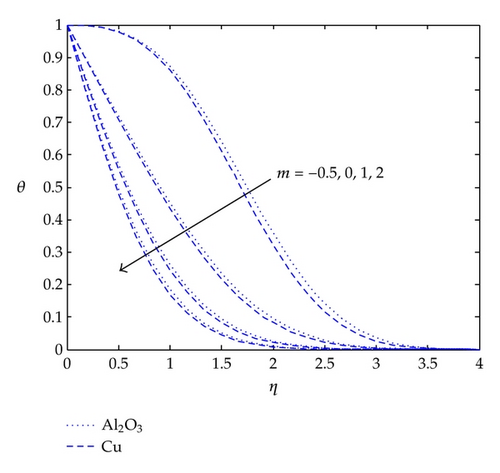
Figure 4 is plotted to see the effects of the surface velocity exponent p on the temperature profiles. It can be seen that temperature decreases with an increase in p.
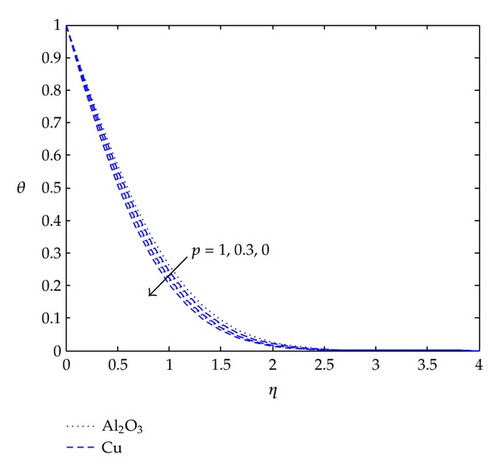
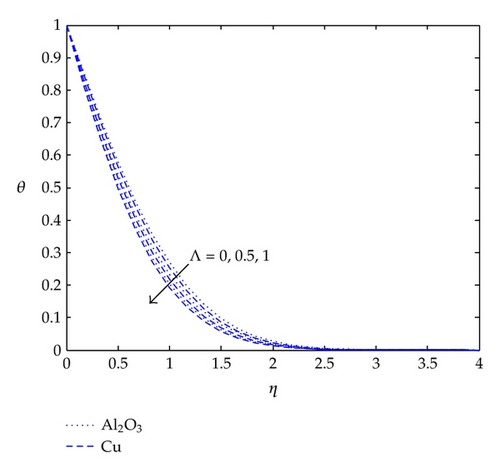
Figure 5 shows the temperatures within the boundary layer region for various values of parameter ∧ (ratio of surface wall velocity to free stream velocity). It is clear that the temperature decreases and the thermal boundary layer thickness becomes thinner when the parameter ∧ takes on a higher value. It is also noticed that the temperature gradient at the surface increases due to enhancements in convective heat transfer.
Tables 3 and 4 show the variations of the surface temperature gradient and local Nusselt number for various values of the volume fraction and streamwise location for copper-water and alumina-water nanofluids, respectively. It is obvious that the surface temperature gradient decreases with the increase of volume fraction; however, the local Nusselt number increases for both cases of the nanofluid. This is attributed to the increase in effective thermal conductivity with ψ as illustrated in the tables. In addition to this, the temperature gradient values increase along the streamwise location.
| ξ = 0.1 | ξ = 0.5 | ||||
|---|---|---|---|---|---|
| ψ | keff/kf | −θ(0) | −θ(0) | ||
| 0.0 | 1.0000 | 1.0426 | 1.0426 | 1.1896 | 1.1896 |
| 0.01 | 1.0403 | 1.0360 | 1.0778 | 1.1780 | 1.2255 |
| 0.05 | 1.2128 | 1.0037 | 1.2173 | 1.1289 | 1.3691 |
| 0.1 | 1.4582 | 0.9557 | 1.3936 | 1.0646 | 1.5524 |
| ξ = 0.1 | ξ = 0.5 | ||||
|---|---|---|---|---|---|
| ψ | keff/kf | −θ(0) | −θ(0) | ||
| 0.0 | 1.0000 | 1.0426 | 1.0426 | 1.1896 | 1.1896 |
| 0.01 | 1.0386 | 1.0288 | 1.0688 | 1.1719 | 1.2171 |
| 0.05 | 1.2037 | 0.9749 | 1.1735 | 1.1045 | 1.3295 |
| 0.1 | 1.4371 | 0.9108 | 1.3089 | 1.0261 | 1.4746 |
4. Concluding Remarks
This paper deals with the effects of different types of nanoparticles on the heat transfer from a continuously moving stretching surface in a concurrent, parallel free stream. The governing equations are derived using the boundary layer approximation and reduced to local nonsimilar ones. Resulting equations are solved numerically. Dimensionless temperature profiles are shown graphically for various problem parameters. It is found that the heat transfer rate increases with the increase of suspended nanoparticle volume fraction. The highest heat transfer enhancement is obtained when Cu nanoparticles are used. It is also concluded that the thermal boundary layer thickness for Al2O3-water nanofluid is higher than that of Cu-water nanofluid.




