Volume 2012, Issue 1 575387

Research Article

Open Access

New Traveling Wave Solutions of the Higher Dimensional Nonlinear Partial Differential Equation by the Exp-Function Method

Hasibun Naher,

Corresponding Author

Hasibun Naher

[email protected]

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia usm.my

Department of Mathematics and Natural Sciences, Brac University, 66 Mohakhali, Dhaka 1212, Bangladesh bracu.ac.bd

Search for more papers by this author

Farah Aini Abdullah,

Farah Aini Abdullah

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia usm.my

Search for more papers by this author

M. Ali Akbar,

M. Ali Akbar

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia usm.my

Department of Applied Mathematics, University of Rajshahi, Rajshahi, Bangladesh ru.ac.bd

Search for more papers by this author

Hasibun Naher,

Corresponding Author

Hasibun Naher

[email protected]

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia usm.my

Department of Mathematics and Natural Sciences, Brac University, 66 Mohakhali, Dhaka 1212, Bangladesh bracu.ac.bd

Search for more papers by this author

Farah Aini Abdullah,

Farah Aini Abdullah

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia usm.my

Search for more papers by this author

M. Ali Akbar,

M. Ali Akbar

School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia usm.my

Department of Applied Mathematics, University of Rajshahi, Rajshahi, Bangladesh ru.ac.bd

Search for more papers by this author

First published: 24 January 2012

https://doi.org/10.1155/2012/575387

Citations: 45

Academic Editor: A. A. Soliman

Share a link

Email
Wechat
Bluesky

Abstract

We construct new analytical solutions of the (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsev equation by the Exp-function method. Plentiful exact traveling wave solutions with arbitrary parameters are effectively obtained by the method. The obtained results show that the Exp-function method is effective and straightforward mathematical tool for searching analytical solutions with arbitrary parameters of higher-dimensional nonlinear partial differential equation.

1. Introduction

Nonlinear partial differential equations (NLPDEs) play a prominent role in different branches of the applied sciences. In recent time, many researchers investigated exact traveling wave solutions of NLPDEs which play a crucial role to reveal the insight of complex physical phenomena. In the past several decades, a variety of effective and powerful methods, such as variational iteration method [1–3], tanh-coth method [4], homotopy perturbation method [5–7], Fan subequation method [8], projective Riccati equation method [9], differential transform method [10], direct algebraic method [11], first integral method [12], Hirota’s bilinear method [13], modified extended direct algebraic method [14], extended tanh method [15], Backlund transformation [16], bifurcation method [17], Cole-Hopf transformation method [18], sech-tanh method [19], (G′/G)-expansion method [20–22], modified (G′/G)-expansion method [23], multiwave method [24], extended (G′/G)-expansion method [25, 26], and others [27–33] were used to seek exact traveling wave solutions of the nonlinear evolution equations (NLEEs).

Recently, He and Wu [34] have presented a novel method called the Exp-function method for searching traveling wave solutions of the nonlinear evolution equations arising in mathematical physics. The Exp-function method is widely used to many kinds of NLPDEs, such as good Boussinesq equations [35], nonlinear differential equations [36], higher-order boundary value problems [37], nonlinear problems [38], Calogero-Degasperis-Fokas equation [39], nonlinear reaction-diffusion equations [40], 2D Bratu type equation [41], nonlinear lattice differential equations [42], generalized-Zakharov equations [43], (3 + 1)-dimensional Jimbo-Miwa equation [44], modified Zakharov-Kuznetsov equation [45], Brusselator reaction diffusion model [46], nonlinear heat equation [47], and the other important NLPDEs [48–51].

In this article, we apply the Exp-function method [34] to obtain the analytical solutions of the nonlinear partial differential equation, namely, (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsev equation.

2. Description of the Exp-Function Method

Consider the general nonlinear partial differential equation

(2.1)

The main steps of the Exp-function method [34] are as follows.

Step 1. Consider a complex variable as

(2.2)

Now using (2.2), (2.1) converts to a nonlinear ordinary differential equation for u(η)

(2.3)

where primes denote the ordinary derivative with respect to η.

Step 2. We assume that the traveling wave solution of (2.3) can be expressed in the form [34]

(2.4)

where c, d, p, and q are positive integers to be determined later, and a_n and b_m are unknown constants. Equation (2.4) can be rewritten in the following equivalent form:

(2.5)

Step 3. In order to determine the values of c and p, we balance the highest order linear term with the highest order nonlinear term, and, determining the values of d and q, we balance the lowest order linear term with the lowest order nonlinear term in (2.3). Thus, we obtain the values of c, d, p, and q.

Step 4. Substituting the values of c, d, p, and q into (2.5), and then substituted (2.5) into (2.3) and simplifying, we obtain

(2.6)

Then each coefficient C_i = 0 is to set, yields a system of algebraic equations for a_c′s and b_p′s.

Step 5. We assume that the unknown a_c′s and b_p′s can be determined by solving the system of algebraic equations obtained in Step 4. Putting these values into (2.5), we obtain exact traveling wave solutions of the (2.1).

3. Application of the Method

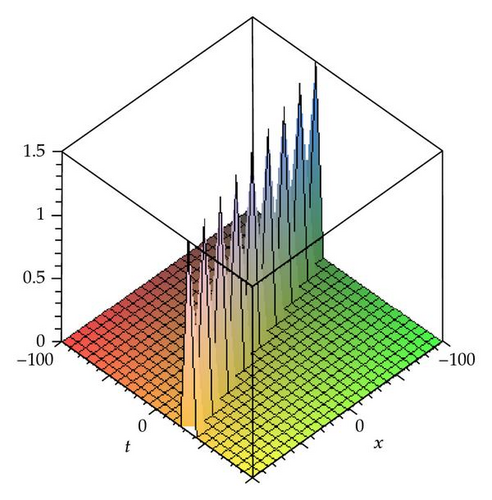
In this section, we apply the method to construct the traveling wave solutions of the (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsev equation. The obtained solutions will be displayed in Figures 1, 2, 3, 4, 5, and 6 by using the software Maple 13.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Periodic solution for α = −1, y = 0 and z = 0.

We consider the (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsev equation

(3.1)

where α is a nonzero constant.

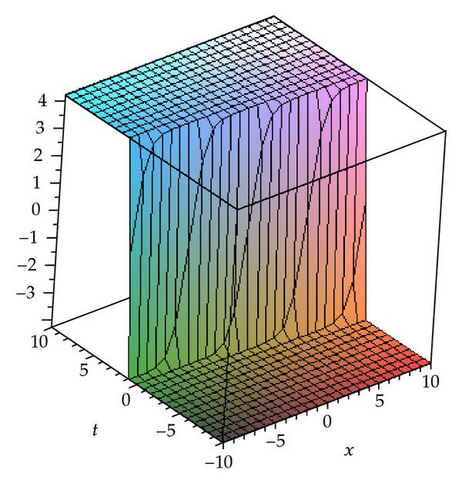
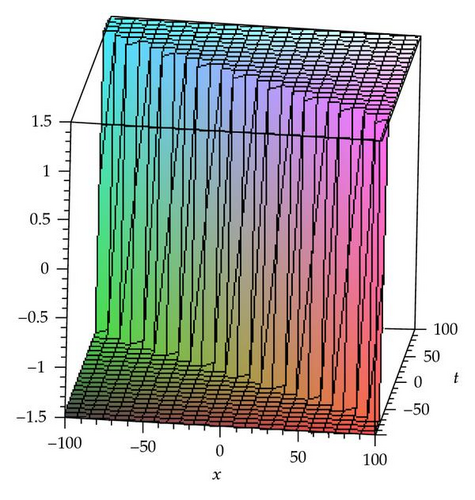
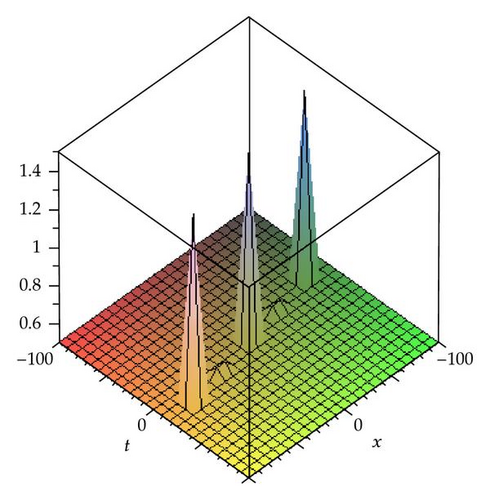
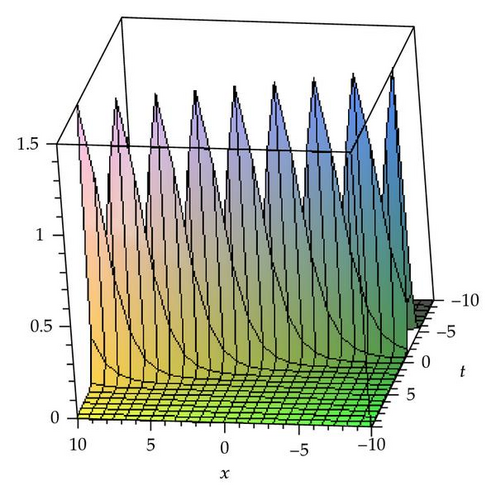
Zayed [52] solved (3.1) using the (G′/G)-expansion method. Later, in article [53], he solved same equation by the generalized (G′/G)-expansion method.

Here, we will solve this equation by the Exp-function method.

Now, we use the transformation (2.2) into (3.1), which yields

(3.2)

where primes denote the derivatives with respect to η.

According to Step 2, the solution of (3.2) can be written in the form of (2.5). To determine the values of c and p, according to Step 3, we balance the highest order linear term of u′′′ with the highest order nonlinear term of u²u′ in (3.2), that is, u′′′ and u²u′. Therefore, we have the following:

(3.3)

where c_j are coefficients only for simplicity; from (3.3), we obtain that

(3.4)

To determine the values of d and q, we balance the lowest order linear term of u′′′ with the lowest order nonlinear term of u²u′ in (3.2). We have

(3.5)

where d_j are determined coefficients only for simplicity; from (3.5), we obtain

(3.6)

Any real values can be considered for c and d, since they are free parameters. But the final solutions of (3.1) do not depend upon the choice of c and d.

Case 1. We set p = c = 1 and q = d = 1.

For this case, the trial solution (2.5) reduces to

(3.7)

Since, b₁ ≠ 0, (3.7) can be simplified

(3.8)

By substituting (3.8) into (3.2) and equating the coefficients of exp (± nη), n = 0,1, 2,3, …, with the aid of Maple 13, we obtain a set of algebraic equations in terms of a₋₁, a₀, a₁, b₋₁, b₀, and V

(3.9)

And, setting each coefficient of exp (± nη), n = 0,1, 2,3, …, to zero, we obtain

(3.10)

For determining unknowns, we solve the obtained system of algebraic (3.10) with the aid of Maple 13, and we obtain four different sets of solutions.

Set 1. We obtain that

(3.11)

where b₋₁ is free parameter.

Set 2. We obtain that

(3.12)

where a₀ and b₀ are free parameters.

Set 3. We obtain that

(3.13)

where a₁ and b₀ are free parameters.

Set 4. We obtain that

(3.14)

where a₀ is free parameter.

Now, substituting (3.11) into (3.8), we obtain traveling wave solution

(3.15)

Equation (3.15) can be simplified as

(3.16)

where η = x + y + z + 6 t.

If b₋₁ = 1 from (3.16), we obtain

(3.17)

Substituting (3.12) into (3.8) and simplifying, we get traveling wave solution

(3.18)

where η = x + y + z + (3/2)t.

If α is negative, that is, α = −β, β > 0, b₀ = 2 and a₀ = 0, then from (3.18), we obtain

(3.19)

Substituting (3.13) into (3.8) and simplifying, we obtain

(3.20)

where

If b₀ = 1, α = 6, and a₁ = 1/2, (3.20) becomes

(3.21)

Substituting (3.14) into (3.8) and simplifying, we obtain

(3.22)

where η = x + y + z − 3t.

If a₀ = 3 and α = 8, (3.22) becomes

(3.23)

Case 2. We set p = c = 2 and q = d = 1.

For this case, the trial solution (2.5) reduces to

(3.24)

Since, there are some free parameters in (3.24), for simplicity, we may consider that b₂ = 1 and b₋₁ = 0. Then the solution (3.24) is simplified as

(3.25)

Performing the same procedure as described in Case 1, we obtain four sets of solutions.

Set 1. We obtain that

(3.26)

where b₀ is free parameter.

Set 2. We obtain that

(3.27)

where a₁ and b₁ are free parameters.

Set 3. We obtain that

(3.28)

where a₂ and b₁ are free parameters.

Set 4. We obtain that

(3.29)

where a₁ is a free parameter.

Using (3.26) into (3.25) and simplifying, we obtain that

(3.30)

If b₀ = 1, from (3.30), we obtain that

(3.31)

where η = x + y + z + 6t.

Substituting (3.27) into (3.25) and simplifying, we obtain that

(3.32)

If α is negative, that is, α = −β, β > 0, b₁ = 2 and a₁ = 0, (3.32) can be simplified as

(3.33)

where η = x + y + z + (3/2)t.

Substituting (3.28) into (3.25) and simplifying, we obtain that

(3.34)

If b₁ = 1, α = 6, and a₂ = 1/2, (3.34) becomes

(3.35)

where

Using (3.29) into (3.25) and simplifying, we obtain that

(3.36)

If a₁ = 3, and α = 8, (3.36) becomes

(3.37)

where η = x + y + z − 3t.

Case 3. We set p = c = 2 and q = d = 2.

For this case, the trial solution (2.5) reduces to

(3.38)

Since, there are some free parameters in (3.38), we may consider b₂ = 1, a₋₂ = 0, b₋₂ = 0, and b₋₁ = 0 so that the (3.38) reduces to the (3.25). This indicates that the Case 3 is equivalent to the Case 2. Equation (3.38) can be rewritten as

(3.39)

If we put a₋₂ = 0, a₋₁ = 0, b₂ = 1, b₋₂ = 0, and b₋₁ = 0 into (3.39), we obtain the solution form as (3.8). This implies that the Case 3 is equivalent to the Case 1.

Also, if we consider p = c = 3 and q = d = 3, it can be shown that this Case is also equivalent to the Cases 1 and 2.

Therefore, we think that no need to find the solutions again.

It is noted that the solution (3.17) and (3.31) are identical, solution (3.19) and (3.33) are identical, solution (3.21) and (3.35) are identical, and solution (3.23) and (3.37) are identical.

Beyond Table 1, Zayed [52] obtained another solution (3.39). But, we obtain two more new solutions (3.21) and (3.23).

Table 1. Comparison between Zayed [52] solutions and our solutions.

Zayed [52] solutions	Our solutions
(i) If λ = 2, μ = 0, equation (3.40) becomes .	(i) Solution (3.17) is .
(ii) If 1 + λ² = 4μ and α is replaced with β, equation (3.38) becomes .	(ii) If η is replaced with iη, solution (3.19) becomes .

Graphical Representations of the Solutions The above solutions are shown with the aid of Maple 13 in the graphs.

4. Conclusions

Using the Exp-function method, with the aid of symbolic computation software Maple 13, new exact traveling wave solutions of the (3 + 1)-dimensional modified KdV-Zakharov-Kuznetsev equation are constructed. It is important that some of the obtained solutions are identical to the solutions available in the literature and some are new. These solutions can be used to describe the insight of the complex physical phenomena.

Acknowledgment

This paper is supported by USM short-term Grant no. 304/PMATHS/6310072, and the authors would like to express their thanks to the School of Mathematical Sciences, USM for providing related research facilities. The authors are also grateful to the referee(s) for their valuable comments and suggestions.

References

1 Abdou M. A. and Soliman A. A., Variational iteration method for solving Burger′s and coupled Burger′s equations, Journal of Computational and Applied Mathematics. (2005) 181, no. 2, 245–251, https://doi.org/10.1016/j.cam.2004.11.032, 2146836.
10.1016/j.cam.2004.11.032
Web of Science® Google Scholar
2 Abdou M. A. and Soliman A. A., New applications of variational iteration method, Physica D. (2005) 211, no. 1-2, 1–8, 2200437, https://doi.org/10.1016/j.physd.2005.08.002, ZBL1084.35539.
10.1016/j.physd.2005.08.002
CAS Web of Science® Google Scholar
3 Gómez C. A. and Salas A. H., Exact solutions for the generalized BBM equation with variable coefficients, Mathematical Problems in Engineering. (2010) 2010, 10, 498249, 2606912, ZBL1191.65163.
10.1155/2010/498249
Web of Science® Google Scholar
4 Wazwaz A. M., The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations, Applied Mathematics and Computation. (2007) 188, no. 2, 1467–1475, 2335643, https://doi.org/10.1016/j.amc.2006.11.013, ZBL1119.65100.
10.1016/j.amc.2006.11.013
Web of Science® Google Scholar
5 Öziş T. and Yildirim A., Traveling wave solution of Korteweg-de vries equation using He′s Homotopy Perturbation Method, International Journal of Nonlinear Sciences and Numerical Simulation. (2007) 8, no. 2, 239–242, 2-s2.0-34249884542.
10.1515/IJNSNS.2007.8.2.239
Web of Science® Google Scholar
6 Zayed E. M. E., Nofal T. A., and Gepreel K. A., On using the homotopy perturbation method for finding the travelling wave solutions of generalized nonlinear Hirota-Satsuma coupled KdV equations, International Journal of Nonlinear Science. (2009) 7, no. 2, 159–166, 2496725.
Google Scholar
7 Mohyud-Din S. T., Yildirim A., and Demirli G., Traveling wave solutions of Whitham-Broer-Kaup equations by homotopy perturbation method, Journal of King Saud University (Science). (2010) 22, no. 3, 173–176, 2-s2.0-77954349361, https://doi.org/10.1016/j.jksus.2010.04.008.
10.1016/j.jksus.2010.04.008
Google Scholar
8 Feng D. and Li K., Exact traveling wave solutions for a generalized Hirota-Satsuma coupled KdV equation by Fan sub-equation method, Physics Letters. A. (2011) 375, no. 23, 2201–2210, https://doi.org/10.1016/j.physleta.2011.04.039, 2800434.
10.1016/j.physleta.2011.04.039
CAS Web of Science® Google Scholar
9 Salas A., Some exact solutions for the Caudrey-Dodd-Gibbon equation, arXiv: 0805.2969v2 [math-ph] 21 May 2008.
Google Scholar
10 Biazar J., Eslami M., and Islam M. R., Differential transform method for nonlinear parabolic-hyperbolic partial differential equations, Applications and Applied Mathematics. (2010) 5, no. 10, 1493–1503, 2747839, ZBL1209.35007.
Google Scholar
11 Taheri S. M. and Neyrameh A., Complex solutions of the regularized long wave equation, World Applied Sciences Journal. (2011) 12, no. 9, 1625–1628.
Google Scholar
12 Sharma P. and Kushel O. Y., The first integral method for Huxley equation, International Journal of Nonlinear Science. (2010) 10, no. 1, 46–52, 2721068.
Web of Science® Google Scholar
13 Wazwaz A.-M., Non-integrable variants of Boussinesq equation with two solitons, Applied Mathematics and Computation. (2010) 217, no. 2, 820–825, https://doi.org/10.1016/j.amc.2010.06.022, 2678596, ZBL1198.35242.
10.1016/j.amc.2010.06.022
Web of Science® Google Scholar
14 Soliman A. A. and Abdo H. A., New exact solutions of nonlinear variants of the RLW, and PHI-four and Boussinesq equations based on modified extended direct algebraic method, International Journal of Nonlinear Science. (2009) 7, no. 3, 274–282, 2538454.
Google Scholar
15 Wazwaz A. M., New travelling wave solutions to the Boussinesq and the Klein-Gordon equations, Communications in Nonlinear Science and Numerical Simulation. (2008) 13, no. 5, 889–901, 2372135, https://doi.org/10.1016/j.cnsns.2006.08.005, ZBL1221.35372.
10.1016/j.cnsns.2006.08.005
Web of Science® Google Scholar
16 Jianming L., Jie D., and Wenjun Y., Backlund transformation and new exact solutions of the Sharma-Tasso-Olver equation, Abstract and Applied Analysis. (2011) 2011, 8, 935710, 2795074, ZBL1217.37057.
10.1155/2011/935710
Google Scholar
17 Song M., Li S., and Cao J., New exact solutions for the (2+1)-dimensional Broer-Kaup-Kupershmidt equations, Abstract and Applied Analysis. (2010) 2010, 9, 652649, 2746008.
10.1155/2010/652649
Google Scholar
18 Salas A. H. and Gómez S. C. A., Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation, Mathematical Problems in Engineering. (2010) 2010, 14, 194329, 2606914, ZBL1191.35236.
10.1155/2010/194329
Web of Science® Google Scholar
19 Sayed S. M., Elhamahmy O. O., and Gharib G. M., Travelling wave solutions for the KdV-Burgers-Kuramoto and nonlinear Schrödinger equations which describe pseudospherical surfaces, Journal of Applied Mathematics. (2008) 2008, 10, 576783, 2447470, ZBL1162.35449.
10.1155/2008/576783
Google Scholar
20 Liu X., Tian L., and Wu Y., Application of (G′/G)-expansion method to two nonlinear evolution equations, Applied Mathematics and Computation. (2010) 217, no. 4, 1376–1384, https://doi.org/10.1016/j.amc.2009.05.019, 2727375.
10.1016/j.amc.2009.05.019
Web of Science® Google Scholar
21 Zheng B., Travelling wave solutions of two nonlinear evolution equations by using the (G′/G) -expansion method, Applied Mathematics and Computation. (2011) 217, no. 12, 5743–5753, https://doi.org/10.1016/j.amc.2010.12.052, 2770192.
10.1016/j.amc.2010.12.052
Google Scholar
22 Feng J., Li W., and Wan Q., Using (G′/G) -expansion method to seek the traveling wave solution of Kolmogorov-Petrovskii-Piskunov equation, Applied Mathematics and Computation. (2011) 217, no. 12, 5860–5865, https://doi.org/10.1016/j.amc.2010.12.071, 2770205.
10.1016/j.amc.2010.12.071
Web of Science® Google Scholar
23 Miao X. J. and Zhang Z. Y., The modified (G′/G) -expansion method and traveling wave solutions of nonlinear the perturbed nonlinear Schrodinger’s equation with Kerr law nonlinearity, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, 4259–4267.
10.1016/j.cnsns.2011.03.032
Web of Science® Google Scholar
24 Shi Y., Dai Z., Han S., and Huang L., The multi-wave method for nonlinear evolution equations, Mathematical & Computational Applications. (2010) 15, no. 5, 776–783, 2777685, ZBL1218.35068.
10.3390/mca15050776
Google Scholar
25 Zayed E. M. E. and El-Malky M. A. S., The Extended (G′/G) -expansion method and its applications for solving the (3+1)-dimensional nonlinear evolution equations in mathematical physics, Global journal of Science Frontier Research. (2011) 11, no. 1.
Google Scholar
26 Zayed E. M. E. and Al-Joudi S., Applications of an extended (G′/G) -expansion method to find exact solutions of nonlinear PDEs in mathematical physics, Mathematical Problems in Engineering. (2010) 2010, 19, 768573, 2674244.
10.1155/2010/768573
Web of Science® Google Scholar
27 Ling-xiao L., Er-qiang L., and Ming-Liang W., The (G′/G,1/G)-expansion method and its application to travelling wave solutions of the Zakharov equations, Applied Mathematics. (2010) 25, no. 4, 454–462, 2746359, https://doi.org/10.1007/s11766%2D010%2D2128%2Dx.
10.1007/s11766-010-2128-x
Google Scholar
28 Abdollahzadeh M., Hosseini M., Ghanbarpour M., and Shirvani H., Exact travelling solutions for fifth order Caudrey-Dodd-Gibbon equation, International Journal of Applied Mathematics and Computation. (2010) 2, no. 4, 81–90.
Google Scholar
29 Gepreel K. A., Exact solutions for nonlinear PDEs with the variable coefficients in mathematical physics, Journal of Information and Computing Science. (2011) 6, no. 1, 003–014.
Google Scholar
30 El-Wakil S. A., Degheidy A. R., Abulwafa E. M., Madkour M. A., Attia M. T., and Abdou M. A., Exact travelling wave solutions of generalized Zakharov equations with arbitrary power nonlinearities, International Journal of Nonlinear Science. (2009) 7, no. 4, 455–461, 2539177.
Google Scholar
31 Zhao Z., Dai Z., and Wang C., Extend three-wave method for the (1+2)-dimensional Ito equation, Applied Mathematics and Computation. (2010) 217, no. 5, 2295–2300, 2727978, https://doi.org/10.1016/j.amc.2010.06.059.
10.1016/j.amc.2010.06.059
Web of Science® Google Scholar
32 Zhou J., Tian L., and Fan X., Soliton and periodic wave solutions to the osmosis K(2,2) equation, Mathematical Problems in Engineering. (2009) 2009, 10, 509390, 2552564, ZBL1182.37038.
10.1155/2009/509390
Web of Science® Google Scholar
33 Khan Y., Faraz N., and Yildirim A., New soliton solutions of the generalized Zakharov equations using He′s variational approach, Applied Mathematics Letters. (2011) 24, no. 6, 965–968, https://doi.org/10.1016/j.aml.2011.01.006, 2776168, ZBL1211.35071.
10.1016/j.aml.2011.01.006
Web of Science® Google Scholar
34 He J.-H. and Wu X.-H., Exp-function method for nonlinear wave equations, Chaos, Solitons and Fractals. (2006) 30, no. 3, 700–708, https://doi.org/10.1016/j.chaos.2006.03.020, 2238695, ZBL1141.35448.
10.1016/j.chaos.2006.03.020
Web of Science® Google Scholar
35 Mohyud-Din S. T., Noor M. A., and Waheed A., Exp-function method for generalized traveling solutions of good Boussinesq equations, Journal of Applied Mathematics and Computing. (2009) 30, no. 1-2, 439–445, 2496628, https://doi.org/10.1007/s12190%2D008%2D0183%2D8, ZBL1176.65112.
10.1007/s12190-008-0183-8
Google Scholar
36 Mohyud-Din S. T., Solution of nonlinear differential equations by exp-function method, World Applied Sciences Journal. (2009) 7, 116–147.
Google Scholar
37 Mohyud-Din S. T., Noor M. A., and Noor K. I., Exp-function method for solving higher-order boundary value problems, Bulletin of the Institute of Mathematics. Academia Sinica. New Series. (2009) 4, no. 2, 219–234, 2541795, ZBL1175.65083.
Google Scholar
38 Mohyud-Din S. T., Noor M. A., and Noor K. I., Some relatively new techniques for nonlinear problems, Mathematical Problems in Engineering. (2009) 2009, 25, 234849, 2530067, ZBL1184.35280.
10.1155/2009/234849
Web of Science® Google Scholar
39 Mohyud-Din S. T., Noor M. A., and Waheed A., Exp-function method for generalized travelling solutions of calogero-degasperis-fokas equation, Zeitschrift fur Naturforschung: Section A Journal of Physical Sciences. (2010) 65, no. 1, 78–84, 2-s2.0-77955943505.
10.1515/zna-2010-1-208
CAS Web of Science® Google Scholar
40 Yildirim A. and Pnar Z., Application of the exp-function method for solving nonlinear reactiondiffusion equations arising in mathematical biology, Computers and Mathematics with Applications. (2010) 60, no. 7, 1873–1880, 2719706, https://doi.org/10.1016/j.camwa.2010.07.020, ZBL1205.35325.
10.1016/j.camwa.2010.07.020
Web of Science® Google Scholar
41 Misirli E. and Gurefe Y., Exp-function method for solving nonlinear evolution equations, Computers and Mathematics with Applications. (2011) 16, no. 1, 258–266, 2-s2.0-77956842939, https://doi.org/10.1016/j.camwa.2010.08.060.
10.3390/mca16010258
Google Scholar
42 Aslan I., Application of the exp-function method to nonlinear lattice differential equations for multi-wave and rational solutions, Mathematical Methods in the Applied Sciences. (2011) 34, no. 14, 1707–1710, https://doi.org/10.1002/mma.1476.
10.1002/mma.1417
Web of Science® Google Scholar
43 Li Y. Z., Li K. M., and Lin C., Exp-function method for solving the generalized-Zakharov equations, Applied Mathematics and Computation. (2008) 205, no. 1, 197–201, 2466623, https://doi.org/10.1016/j.amc.2008.05.138, ZBL1160.35523.
10.1016/j.amc.2008.05.138
Web of Science® Google Scholar
44 Öziş T. and Aslan I., Exact and explicit solutions to the (3+1)-dimensional Jimbo-Miwa equation via the Exp-function method, Physics Letters, Section A. (2008) 372, no. 47, 7011–7015, 2468981, https://doi.org/10.1016/j.physleta.2008.10.014.
10.1016/j.physleta.2008.10.014
CAS Web of Science® Google Scholar
45 Mohyud-Din S. T., Noor M. A., and Noor K. I., Exp-function method for traveling wave solutions of modified Zakharov-Kuznetsov equation, Journal of King Saud University. (2010) 22, no. 4, 213–216, 2-s2.0-77952378676, https://doi.org/10.1016/j.jksus.2010.04.015.
10.1016/j.jksus.2010.04.015
Google Scholar
46 Khani F., Samadi F., and Hamedi-Nezhad S., New exact solutions of the Brusselator reaction diffusion model using the exp-function method, Mathematical Problems in Engineering. (2009) 2009, 9, 346461, 2539716, ZBL1184.35099.
10.1155/2009/346461
Web of Science® Google Scholar
47 Zhang W., The extended tanh method and the exp-function method to solve a kind of nonlinear heat equation, Mathematical Problems in Engineering. (2010) 12, 935873, 2726308, ZBL1205.65279.
Web of Science® Google Scholar
48 Parand K., Rad J. A., and Rezaei A., Application of Exp-function method for a class of nonlinear PDE′s arising in mathematical physics, Journal of Applied Mathematics & Informatics. (2011) 29, no. 3-4, 763–779.
Google Scholar
49 Yao L., Wang L., and Zhou X.-W., Application of exp-function method to a Huxley equation with variable coefficient, International Mathematical Forum. (2009) 4, no. 1–4, 27–32, 2476533, ZBL1169.65104.
Google Scholar
50 Salas A. H. and Gómez S C. A., Exact solutions for a third-order KdV equation with variable coefficients and forcing term, Mathematical Problems in Engineering. (2009) 2009, 13, 737928, 2578371, ZBL1188.35168.
10.1155/2009/737928
Web of Science® Google Scholar
51 Akbar M. A. and Ali N. H. M., Exp-function method for duffing equation and new solutions of (2+1) dimensional dispersive long wave equations, Progress in Applied Mathematics. (2011) 1, no. 2, 30–42.
Google Scholar
52 Zayed E. M. E., Traveling wave solutions for higher dimensional nonlinear evolution equations using the (G′/G) -expansion method, Journal of Applied Mathematics & Informatics. (2010) 28, no. 1-2, 383–395.
Google Scholar
53 Zayed E. M. E., New traveling wave solutions for higher dimensional nonlinear evolution equations using a generalized (G′/G) -expansion method, Journal of Physics A: Mathematical and Theoretical. (2009) 42, no. 19, article 195202, https://doi.org/10.1088/1751%2D8113/42/19/195202, 2599319.
10.1088/1751-8113/42/19/195202
Web of Science® Google Scholar

Citing Literature

All articles

New Traveling Wave Solutions of the Higher Dimensional Nonlinear Partial Differential Equation by the Exp-Function Method

Abstract

1. Introduction

2. Description of the Exp-Function Method

3. Application of the Method

4. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

New Traveling Wave Solutions of the Higher Dimensional Nonlinear Partial Differential Equation by the Exp-Function Method

Abstract

1. Introduction

2. Description of the Exp-Function Method

3. Application of the Method

4. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Related

Information