This paper presents a new sectional flexibility factor to simulate the reduction of the stiffness of a single-edge open cracked beam. The structural model for crack of the beam is considered as a rotational spring which is related to the ratio of crack depth to the beam height, a/h. The mathematical model of this single-edge open crack beam is considered as an Euler-Bernoulli beam. The modified factor, f(a/h), derived in this paper is in good agreement with previous researchers′ results for crack depth ratio a/h less than 0.5. The natural frequencies and corresponding mode shapes for lateral vibration with different types of single-edge open crack beams can then be evaluated by applying this modified factor f(a/h). Using the compatibility conditions on the crack and the analytical transfer matrix method, the numerical solutions for natural frequencies of the cracked beam are obtained. The natural frequencies and the mode shapes with crack at different locations are obtained and compared with the latest research literature. The numerical results of the proposed cracked beam model obtained by this method can be extended to construct frequency contour. The natural frequencies measured from field can be used in solving the inverse problem to identify cracks in structures.

1. Introduction

A crack in the structure will reduce the structural strength and result in severe damage under critical loading conditions. The major issue of the structural health monitoring is to detect crack depth and location in the present study. The model with linear elastic fracture mechanics and Euler-Bernoulli beam theory are being widely used in the recent research literatures. The cracked beam is modeled as two-segment beam with the crack simulated as a rotational spring. The crack of the beam is considered as a local flexibility which is a function of the crack depth.

Sih [1] proposed strain energy density factor theory to discuss the all mixed-mode crack extension problems. The strain energy density factor is a linear elasticity function of the mixed-mode stress intensity factors. Tada et al. [2] presented the stress intensity factors of different modes due to general loading. The presented model introduced the local flexibility matrix from the stress intensity factors. Nobile [3] proposed a simple method for obtaining approximate stress intensity of straight cracked beams. The system takes account of the elastic crack tip stress singularity while using the elementary beam theory. Dimarogonas and Paipetis [4] introduced a general stiffness matrix for cracked structural members to model the respective dynamic system. The local flexibility can be derived further from the general stiffness matrix. Chondros et al. [5] developed a continuous cracked beam vibration theory for the lateral vibration of cracked Euler-Bernoulli beams with single-edge or double-edge open cracks. The crack was modeled as a continuous flexibility using the displacement field. Anifantis and Dimarogonas [6] studied the system stability of the cracked column with vertical load. The method developed a general flexibility matrix to express the local flexibility of a beam with a single-edge crack. Ostachowicz and Krawczuk [7] developed a new local flexibility which was derived from the stress intensity factor by Anifantis and Dimarogonas [6].

In order to obtain the natural frequencies of the crack beam, finite element method was used to compute the eigensolutions in the recent literatures. The order of the determinants increases as the degree of freedom increases in finite element method. In order to reduce the order of the determinants, Lin et al. [8] proposed using transfer matrix for beams with arbitrary number of cracks. The method uses only four unknown constants which can be solved through satisfying four boundary conditions. Lin and Chang [9] used the analytic transfer matrix method to solve eigensolutions of a cracked cantilever beam. The eigenfunctions obtained in this method are analytical solutions. The dynamic responses can be obtained by this method, and the solutions converge quite fast. Alsabbagh et al. [10] presented a new simplified formula for the stress correction factor by using strain energy density approach. A modified factor for local flexibility was used in solving the characteristic equation of the cracked beam. Lin [11] used the Timoshenko beam theory and transfer matrix method to solve the direct and inverse problems of simply supported beam with a single-edge open crack. The location and crack size of the beam can be determined by the method presented. The theoretical results are also validated by a comparison with experimental measurements.

2. Derivation of Stress Intensity Factor

A prismatic beam is considered with an open and nonpropagating crack of depth a, length L, height h, and width t. The singular stress distribution at the crack tip takes the form [3, 4, 10]

()

with the conditions that

acts at a distance r = b from the tip and K_I is the stress intensity factor. The normal stress acting on the reduced cross-section passing through the crack tip is given as

()

where M is the bending moment and I = t(h−a)³/12 is the moment of inertia of the remaining part of the cracked beam. The distance y in (2.2) is found from Figure 1 as

()

where

is the distance from the neutral axis of the reduced cross-section to the tip as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Geometry of a beam with a single-edge crack.

The stress condition is considered as

at the crack tip r = b. Substituting (2.3) into (2.2), σ_x and K_I can be expressed as

()

The distance b can be determined from the equilibrium condition of forces along the x-axis:

()

The left-hand side of (2.6) is evaluated, using (2.5), to be

()

The right-hand side of (2.6) is evaluated, using (2.4), to be

()

Substitution of (2.7) and (2.8) into (2.6) leads to

()

Substituting (2.10) into (2.5), the stress intensity factor can be expressed as

()

where

()

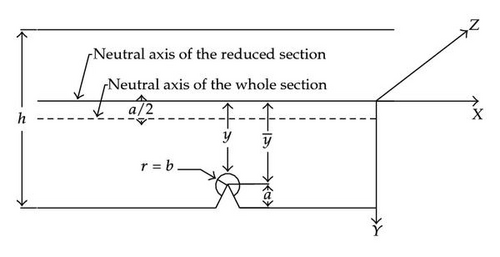
3. Calculation of the Equivalent Flexibility in the Crack Beam

Let U_T be the strain energy due to the crack. According to Castigliano’s theorem, the additional displacement is u_i = ∂U_T/∂P_i under general loading P_i. In this work, the displacement will reduce to

()

where the displacement u_i is taken as the rotation θ since the bending moment M is the only load of the structure.

The strain energy has the form [4–6, 10]

()

where J is the strain energy density function. Therefore,

()

The moment M substitutes for the generalized load P_i

()

The flexibility influence coefficient will be written as

()

The strain energy density function J has the form

()

where E′ = E/(1 − υ²) for plane strain and E and υ are Young’s modulus and Poisson’s ratio, respectively. The flexibility scalar is

()

where Poisson’s ratio is taken as υ = 0.3 and the area moment of inertia is taken for the whole cross-section as I = th³/12. The nondimensional cracked section flexibility can be found from (3.7) as

()

4. Free Vibration of a Cracked Beam

A simple beam with length L and an open-edge crack at position X₁ is considered as shown in Figure 2. Euler-Bernoulli beam bending theory was used in solving the free vibration problem. According to [8, 9], the differential equation of motion for each segment is

()

where ρ is the density of the material and A is the cross-section area of the rectangular beam. The boundary conditions of the simply supported beam are

()

The beam at the crack position is simulated as a rational spring with sectional flexibility as shown in Figure 3. The continuous conditions at the crack position are

()

and the compatibility condition due to the rational flexibility is

()

From the above equations, the following quantities are introduced for nondimensional analysis:

()

Equation (4.1) can then be expressed in a nondimensional form as

()

The continuous conditions at the crack position as non-dimensional form are

()

where c^* is the non-dimensional cracked section flexibility as (3.8).

5. Calculation of Natural Frequencies

The equation of motion for the cracked simple beam system can be expressed as (4.8). Using the method of separation of variables, y_i(x, t) = w_i(x)e^jωt, in (4.8), the differential equation for free vibration can be written as

()

where

()

From (4.9), the continuous conditions at the crack position are

()

A closed-form solution to this eigenvalue problem can be obtained by employing transfer matrix methods [8, 9]. The general solution of (5.1), for each segment, is

()

where A_i, B_i, C_i, and D_i are constants associated with the ith segment (i = 1,2). These constants of the second segment (A₂, B₂, C₂, and D₂) are related to those of the first segment (A₁, B₁, C₁, and D₁) through the continuous conditions in (5.3) and can be expressed as

()

where

is a 4 × 4 transfer matrix which depends on eigenvalue λ and the elements are derived from [8].

Using (5.5), the four constants of the first segment (A₁, B₁, C₁, and D₁) can be mapped into those of the second segment (A₂, B₂, C₂, and D₂); thereby, the number of independent constants can be reduced to four. For the case of a simply supported beam, the corresponding boundary conditions of (4.2) and (4.3) can be written as

()

Due to (5.6) and (5.8), (5.4) yields

()

Satisfying the boundary conditions (5.7) and (5.9), (5.4) leads to the following equations:

()

which can be expressed in matrix form as

()

where

()

Substituting (5.5) into (5.12) and applying (5.10), one obtains

()

where

()

A nontrivial solution of the simply supported beam requires

()

The characteristic equation of the cracked simply supported beam can be obtained as

()

where λ_n is the eigenvalues of the system. This characteristic equation can be solved by using the Newton-Raphson method to obtain the eigenvalues and corresponding eigenfunctions.

6. Numerical Results

In order to verify the procedure presented in this paper, results obtained by applying this method are compared with the available data for single-edge open cracked beam. A 300 mm simple supported beam of cross-section 20 × 20 mm², with modulus of elasticity E = 2.06 × 10¹¹ N/m², the density ρ = 7800 kg/m³, the crack is located at the position 240 mm and crack depth a = 8 mm.

A simplified stress intensity factor K_I in (2.11) is expressed in this paper. The function F(a/h) in (2.12) can be compared with the expression given by [2]

()

Another stress intensity factor is [12]

()

In this research, small crack depth ratio which implies early stage of structure damage is considered. The comparison of data obtained by the proposed method and previous research is shown in Figure 4. The stress intensity factor of the present model and those in [2, 12] are rather close to each other for small crack depth ratio a/h.

The nondimensional cracked section flexibility c^* in (3.8) can be compared with the expression given by [5]

()

Another non-dimensional cracked section flexibility is [7]

()

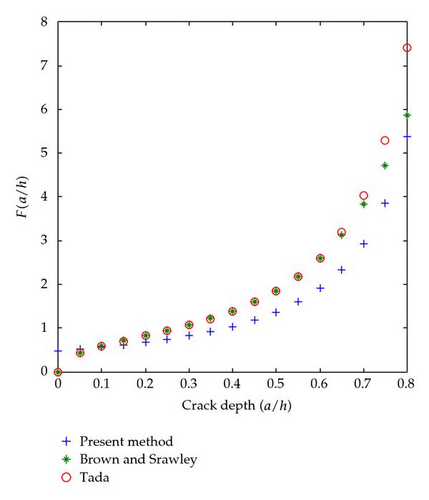
Three generalized loading conditions, bending, tension, and torsion, on a cracked beam were considered to evaluate sectional flexibility in the past literature. Beams are mainly affected by bending moment in most loading cases; therefore only bending effects are considered in evaluating the simplified cracked section flexibility. The results of the proposed method of non-dimensional cracked section flexibility are compared with those of previous research in Figure 5. The results of this simplified method and those of [5, 7] are in good agreement for small crack depth ratio a/h. A cracked beam with a/h greater than 0.5 is already severely damaged and is not suitable for applying this sectional flexibility model.

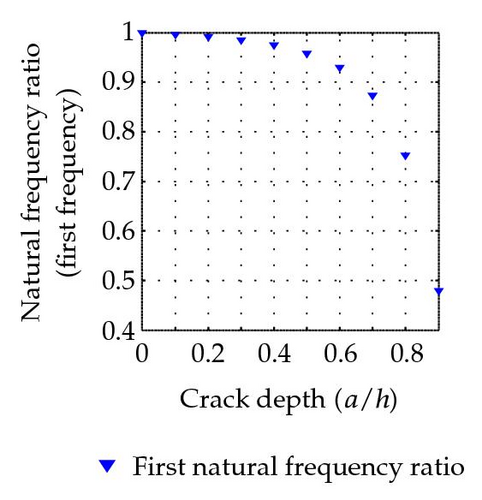
The first five natural frequencies of the uncracked beam are calculated as ω₀₁ = 517.85, ω₀₂ = 2071.4, ω₀₃ = 4660.64, ω₀₄ = 8285.58, and ω₀₅ = 12946.22 Hz. The ratios of natural frequencies between cracked beam and uncracked beam are listed in Table 1. The variation of natural frequency ratio with the crack depth of this simply supported beam with a crack located at the section (L₁/L = 0.8) for the first five modes is plotted as in Figure 6.

Table 1. Natural frequency ratio with the crack depth at location 0.8.

Crack location	Crack depth	Natural frequency ratio
L₁/L	a/h	ω₁/ω₀₁	ω₂/ω₀₂	ω₃/ω₀₃	ω₄/ω₀₄	ω₅/ω₀₅
0.8	0.0	1.0000	1.0000	0.9999	1.0000	0.9999
0.8	0.1	0.9966	0.9912	0.9913	0.9967	0.9999
0.8	0.2	0.9918	0.9792	0.9803	0.9927	0.9999
0.8	0.3	0.9850	0.9628	0.9660	0.9876	0.9999
0.8	0.4	0.9747	0.9394	0.9474	0.9814	0.9999
0.8	0.5	0.9581	0.9052	0.9237	0.9737	0.9999
0.8	0.6	0.9292	0.8544	0.8943	0.9648	0.9999
0.8	0.7	0.8735	0.7800	0.8605	0.9551	0.9999
0.8	0.8	0.7525	0.6809	0.8271	0.9459	0.9999
0.8	0.9	0.4791	0.5825	0.8021	0.9392	0.9999

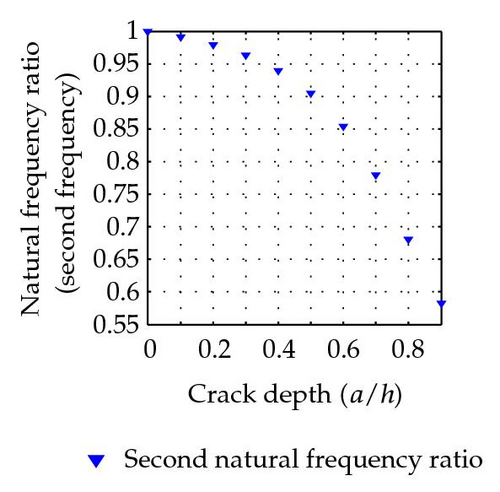
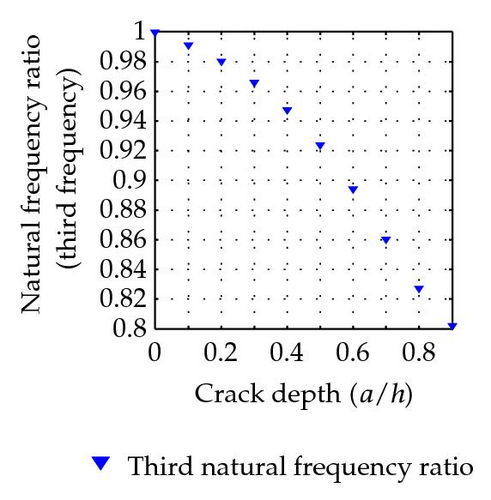
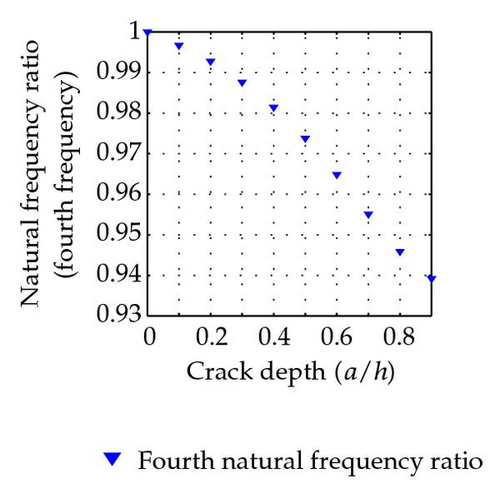
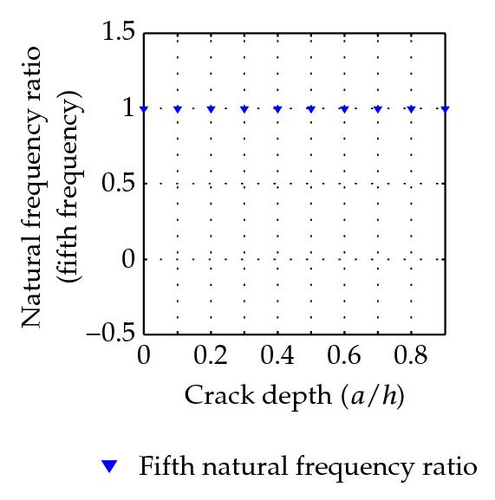
With a crack located at the center of the beam, the ratios of natural frequencies between cracked beam and uncracked beam are listed in Table 2. The variation of natural frequency ratio with the crack depth of a simply supported beam with a crack located at (L₁/L = 0.5) is shown in Figure 7 for the first five modes.

Table 2. Natural frequency ratio with the crack depth at location 0.5.

Crack location	Crack depth	Natural frequency ratio
L₁/L	a/h	ω₁/ω₀₁	ω₂/ω₀₂	ω₃/ω₀₃	ω₄/ω₀₄	ω₅/ω₀₅
0.5	0.0	1.0000	1.0000	0.9999	1.0000	0.9999
0.5	0.1	0.9902	1.0000	0.9904	1.0000	0.9905
0.5	0.2	0.9770	1.0000	0.9778	1.0000	0.9786
0.5	0.3	0.9586	1.0000	0.9613	1.0000	0.9636
0.5	0.4	0.9321	1.0000	0.9391	1.0000	0.9448
0.5	0.5	0.8927	1.0000	0.9094	1.0000	0.9218
0.5	0.6	0.8314	1.0000	0.8699	1.0000	0.8948
0.5	0.7	0.7328	1.0000	0.8199	1.0000	0.8654
0.5	0.8	0.5723	1.0000	0.7634	1.0000	0.8377
0.5	0.9	0.3245	1.0000	0.7144	1.0000	0.8175

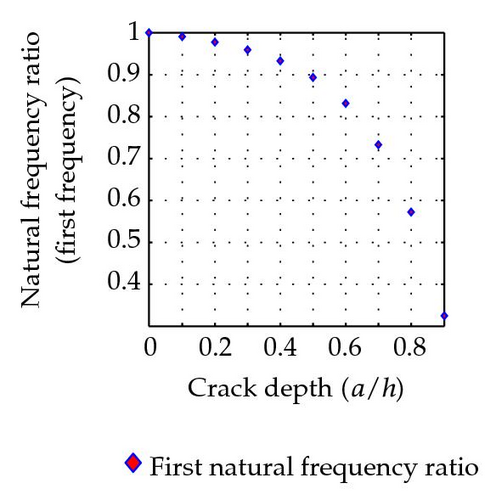
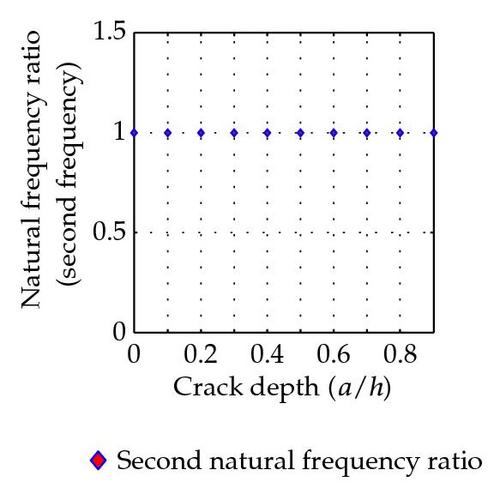
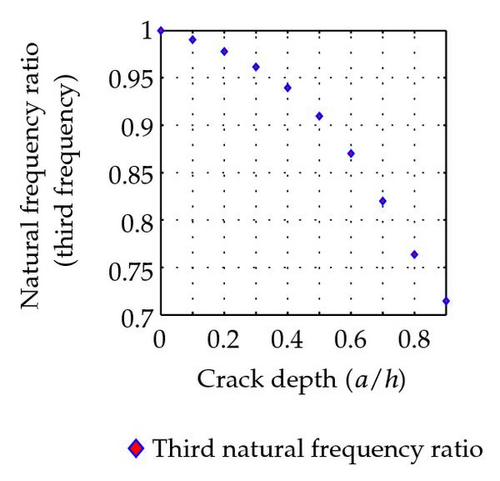
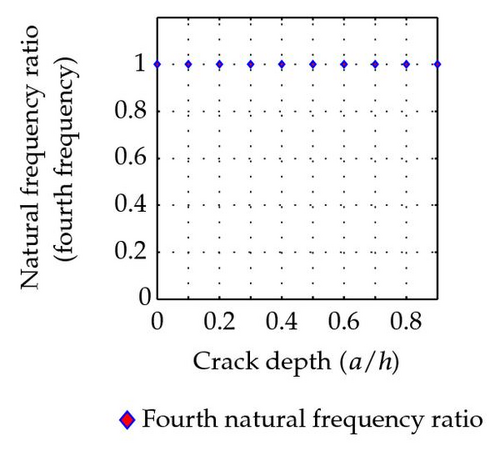
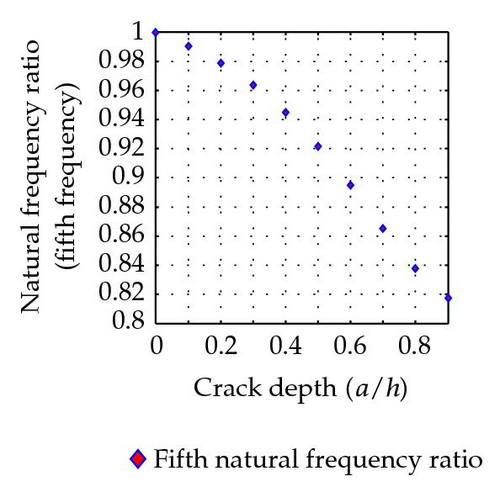
It is quite obvious that the natural frequencies decrease due to the existence of cracks. That is due to the cracked beam becoming more flexible due to the reduction of moment of inertia of the section property.

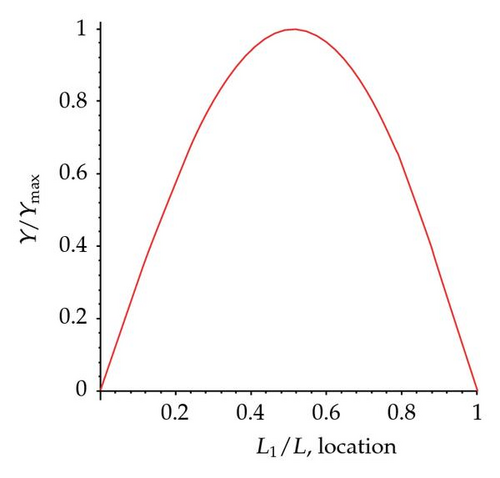
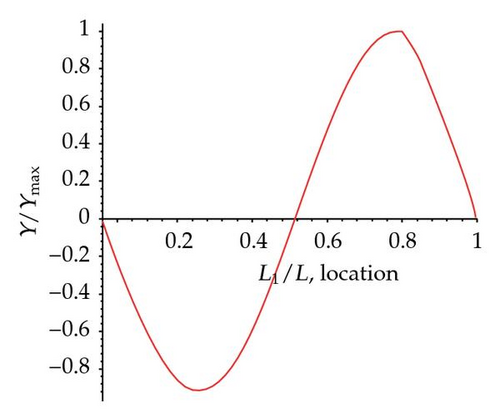
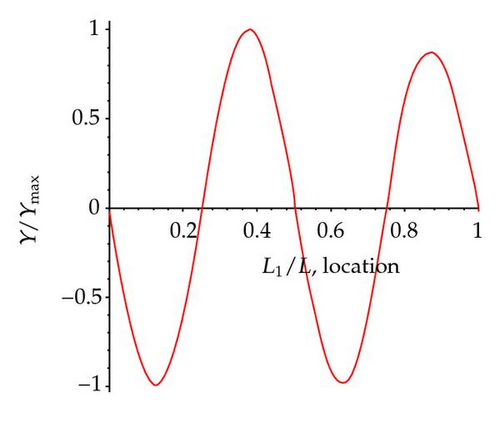
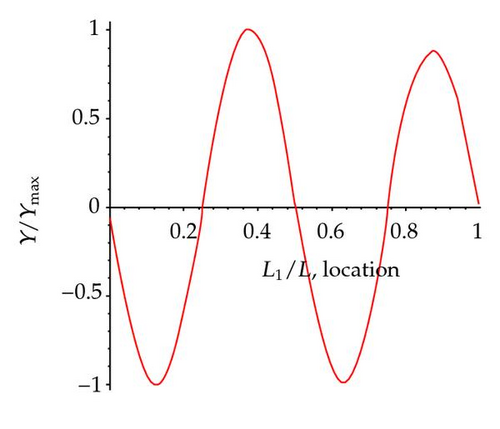
Figures 8(a)–8(e) show the first five mode shapes of a cracked simply supported beam with single open crack at L₁/L = 0.8, crack ratio a/h = 0.4, and normalized amplitude Y/Y_max. It is obvious that the mode shapes all show turning point at crack location L₁/L = 0.8.

7. Conclusion

The simplified stress intensity factor and flexibility were derived utilizing the crack beam theorem of Nobile [3] and Dimarogonas [4, 5]. The order of polynomial functions for crack depth ratio a/h is reduced, because, with a crack depth ratio a/h < 0.5, the high-order terms will approach to 0. Therefore, these higher-order arithmetic terms can be neglected and, in order to predict the early stage of structural damage, crack depth ratio a/h should be less than 0.5. The simplified stress intensity factor and flexibility are compared with the recent literature, and the numerical results are found to be in good agreement.

If the crack is right on the position of nodal point of certain modes, frequencies ratio shows no difference with ω_i/ω_0i = 1. For example, the crack at 0.8 L is also a nodal point of the fifth mode which gives the numerical result as ω₅/ω₀₅ = 1. The numerical results obtained by this method are in good agreement with the actual vibration response of a simply supported beam. The turning points of certain mode shape function reveal the information about crack location. For the case with a crack at 0.8 L, it can be seen obviously from shape function of mode two, mode three, and mode four with a turning point at 0.8 L.

The simplified stress intensity factor and flexibility of this method can be further extended to construct frequencies ratio contours for beams with cracks. The natural frequencies obtained by applying this model can be used to verify the experimental measurements in a similar way to that in [11]. The location and crack depth of a beam can then be identified as an inverse problem by matching up field measurement of frequencies of a cracked beam.

References

1 Sih G. C., Method of Fracture Analysis and Solutions of Crack Problems, 1973, Noordhoff International, Leiden, The Netherlands, 0449095, ZBL0319.73053.
10.1007/978-94-017-2260-5
Google Scholar
2 Tada H., Paris P. C., and Irwin G. R., The Stress Analysis of Cracks Handbook, 1985, 2nd edition, Paris Productions, St. Louis, Mo, USA, ZBL0598.30060.
Google Scholar
3 Nobile L., [email protected], Mixed mode crack initiation and direction in beams with edge crack, Theoretical and Applied Fracture Mechanics. (2000) 33, no. 2, 107–116, https://doi.org/10.1016/S0167%2D8442(00)00006%2D9.
10.1016/S0167-8442(00)00006-9
Web of Science® Google Scholar
4 Dimarogonas A. D. and Paipetis S. A., Analytical Methods in Rotor Dynamics, 1983, Applied Science, New York, NY, USA.
Google Scholar
5 Chondros T. G., Dimarogonas A. D., and Yao J., A continuous cracked beam vibration theory, Journal of Sound and Vibration. (1998) 215, no. 1, 17–34, https://doi.org/10.1006/jsvi.1998.1640.
10.1006/jsvi.1998.1640
Web of Science® Google Scholar
6 Anifantis N. and Dimarogonas A., Stability of columns with a single crack subjected to follower and vertical loads, International Journal of Solids and Structures. (1983) 19, no. 4, 281–291, https://doi.org/10.1016/0020%2D7683(83)90027%2D6, ZBL0523.73042.
10.1016/0020-7683(83)90027-6
Web of Science® Google Scholar
7 Ostachowicz W. M. and Krawczuk M., Analysis of the effect of cracks on the natural frequencies of a cantilever beam, Journal of Sound and Vibration. (1991) 150, no. 2, 191–201, https://doi.org/10.1016/0022%2D460X(91)90615%2DQ.
10.1016/0022-460X(91)90615-Q
Web of Science® Google Scholar
8 Lin H. P., Chang S. C., and Wu J. D., Beam vibrations with an arbitrary number of cracks, Journal of Sound and Vibration. (2002) 258, no. 5, 987–999, https://doi.org/10.1006/jsvi.2002.5184.
10.1006/jsvi.2002.5184
Web of Science® Google Scholar
9 Lin H. P. and [email protected], Chang S. C., Forced responses of cracked cantilever beams subjected to a concentrated moving load, International Journal of Mechanical Sciences. (2006) 48, no. 12, 1456–1463, https://doi.org/10.1016/j.ijmecsci.2006.06.014, ZBL1192.74182.
10.1016/j.ijmecsci.2006.06.014
Web of Science® Google Scholar
10 Alsabbagh A. S. Y., Abuzeid O. M., and [email protected], Dado M. H., Simplified stress correction factor to study the dynamic behavior of a cracked beam, Applied Mathematical Modelling. (2009) 33, no. 1, 127–139, https://doi.org/10.1016/j.apm.2007.10.018, ZBL1167.74572.
10.1016/j.apm.2007.10.018
Web of Science® Google Scholar
11 Lin H. P., [email protected], Direct and inverse methods on free vibration analysis of simply supported beams with a crack, Engineering Structures. (2004) 26, no. 4, 427–436, https://doi.org/10.1016/j.engstruct.2003.10.014.
10.1016/j.engstruct.2003.10.014
Web of Science® Google Scholar
12 Brown W. F. and Srawley J. E., Plane Strain Crack Toughness Testing of High Strength Metallic Material, 1966, American Society Testing and Materials.
10.1520/STP44663S
Google Scholar

Citing Literature

All articles

Modified and Simplified Sectional Flexibility of a Cracked Beam

Abstract

1. Introduction

2. Derivation of Stress Intensity Factor

3. Calculation of the Equivalent Flexibility in the Crack Beam

4. Free Vibration of a Cracked Beam

5. Calculation of Natural Frequencies

6. Numerical Results

7. Conclusion

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Modified and Simplified Sectional Flexibility of a Cracked Beam

Abstract

1. Introduction

2. Derivation of Stress Intensity Factor

3. Calculation of the Equivalent Flexibility in the Crack Beam

4. Free Vibration of a Cracked Beam

5. Calculation of Natural Frequencies

6. Numerical Results

7. Conclusion

References

Citing Literature

Figures

References

Related

Information