Advances in Numerical Analysis
Volume 2012, Issue 1 541083
Research Article
Open Access

New Approach for Solving a Class of Doubly Singular Two-Point Boundary Value Problems Using Adomian Decomposition Method

Randhir Singh, 

Corresponding Author

Randhir Singh

Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 721302, India iitkgp.ac.in

Search for more papers by this author
Jitendra Kumar, 

Jitendra Kumar

Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 721302, India iitkgp.ac.in

Search for more papers by this author
Gnaneshwar Nelakanti, 

Gnaneshwar Nelakanti

Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 721302, India iitkgp.ac.in

Search for more papers by this author
First published: 26 December 2012
https://doi.org/10.1155/2012/541083
Citations: 15
Academic Editor: Norbert Heuer

Abstract

We propose two new modified recursive schemes for solving a class of doubly singular two-point boundary value problems. These schemes are based on Adomian decomposition method (ADM) and new proposed integral operators. We use all the boundary conditions to derive an integral equation before establishing the recursive schemes for the solution components. Thus we develop recursive schemes without any undetermined coefficients while computing successive solution components, whereas several previous recursive schemes have done so. This modification also avoids solving a sequence of nonlinear algebraic or transcendental equations for the undetermined coefficients with multiple roots, which is required to complete calculation of the solution by several earlier modified recursion schemes using the ADM. The approximate solution is computed in the form of series with easily calculable components. The effectiveness of the proposed approach is tested by considering four examples and results are compared with previous known results.

1. Introduction

Consider the following class of doubly singular two-point boundary value problems:
()
with boundary conditions
()
where a1, c1, a > 0, b ≥ 0, and c are any finite constants. The condition p(0) = 0 characterizes that problem (1.1) is singular and in addition to this if q(t) is allowed to be discontinuous at t = 0, then problem (1.1) is called doubly singular Bobisud [1]. Consider problem (1.1) with the following conditions on p(t), q(t), and f(t, y(t)).

Type 1. Dirichlet boundary conditions: y(0) = a1, y(1) = c1

  •  

    (E1) p ∈ C[0,1], p ∈ C1(0,1] with p > 0 in (0,1] and 1/p ∈ L1(0,1);

  •  

    (E2) q > 0 in (0,1] and ;

  •  

    (E3)  (i) f ∈ C([0,1] × ℝ); (ii)  ∂f/∂y exists and continuous, ∂f/∂y ≥ 0 for all 0 ≤ t ≤ 1 and all real y.

Type 2. Mixed type boundary conditions: y′(0) = 0,  ay(1) + by′(1) = c

  •  

     p ∈ C[0,1],  p ∈ C1(0,1] with p > 0 in (0,1];

  •  

     q > 0 in (0,1], q ∈ L1(0,1) and ;

  •  

      the same as (E3).

In recent years, the study of such singular boundary value problems (1.1) has attracted the attention of several researchers [2–9]. In particular, if p(t) = 1,  q(t) = t−1/2 and f(t, y) = y3/2 problem (1.1) with Type 1 boundary conditions is known as Thomas-Fermi equation. Thomas [10] and Fermi [11] independently derived a boundary value problem for determining the electrical potential in an atom. The analysis leads to the nonlinear SBVP y′′ = t−1/2y3/2 with boundary conditions given by y(0) = 1,  y(b1) = 0.

Chan and Hon [12] considered the generalized Thomas-Fermi equation: , y(0) = 1, y(a) = 0 with , where 0 ≤ b2 < 1, c > 0, d2 > −2, e > 1, which is doubly singular problem. Problem (1.1) with q(t) = p(t) = tα where α = 2 arises in the study of the distribution of heat sources in the human head [13] with f(t, y) = −δe−θy, θ > 0, δ > 0.

There is a huge literature available on numerical methods for problem (1.1) with q(t) = 1, but very few numerical methods are available to tackle doubly singular boundary value problems. Reddien [14] studied the linear form of problem (1.1) and derived numerical methods for q(t) ∈ L2[0,1] which is stronger assumption than ().

Chawla and Shivakumar [15] established the existence as well as uniqueness of solution for problem (1.1) where q(t) = p(t) = tα. The existence and uniqueness for problem (1.1) have also been discussed by Dunninger and Kurtz [16] and Bobisud [1]. Later Pandey and Verma [17] extended the results on the existence uniqueness for problem (1.1) with Types 1 and 2 boundary conditions.

1.1. Adomian Decomposition Method (ADM)

In this subsection, we briefly describe standard ADM for nonlinear second-order equation.

Recently, many researchers [4, 18–26] have shown interest to the study of ADM for different scientific models. Adomian [18] asserted that the ADM provides an efficient and computationally suitable method for generating approximate series solution for a large class of differential equations. Let us consider nonlinear second-order ordinary differential equation
()
where L ≡ d2/dt2 is the second-order linear derivative operator, R is the linear remainder operator, N represents the nonlinear term, and g(t) is a source term. The above equation can be rewritten as
()
The inverse operator of L is defined as .
Operating the inverse linear operator L−1(·) on both the sides of (1.4) yields
()
Next, we decompose the solution y and the nonlinear function Ny by an infinite series as
()
where An are Adomian polynomials that can be constructed for various classes of nonlinear functions with the formula given by Adomian and Rach [19]
()
Substituting the series (1.6) into (1.5), we obtain
()
From (1.8), the various components yn of the solution y can be determined by using the recursive relation
()
For numerical purpose, the n-term truncated series may be used to give the approximate solution.

The ADM has been used to solve nonlinear boundary value problems (BVPs) for ordinary differential equations by several researchers [4, 20–26]. Solving nonlinear BVP by standard ADM is always a computationally involved task as it requires the computation of undetermined coefficients y′(0) in (1.9) in a sequence of nonlinear equations which increases computational complexity.

It is important to note that the standard ADM (1.9) can not be applied directly to solve two-point boundary value problem (1.1) as the component y0 in scheme (1.9) is not independent from undetermined coefficient. Many researchers [23–25] have proposed modified ADM to overcome the difficulty by setting undermined coefficient y′(0) = c, and then it will be determined by using second boundary condition satisfying ψn(1) = y(1). In this case, it requires additional computational work to solve nonlinear equation ψn(1) = y(1) for c and c may not be uniquely determined.

Benabidallah and Cherruault [24] have considered the following boundary value problem:
()
The inverse operator was proposed, then unidentified constant y′(b) is set, as , and each solution component yn is obtained by the following scheme:
()
In order to determine the unidentified constants cn, it is also required n-term approximate solution satisfying all the boundary conditions. It is clearly that ψn(a) = y(a). For boundary condition x = b, the following scheme was proposed
()
However, since each constant cn is determined by solving (1.12), this scheme also require additional computational work.

In order to avoid solving such nonlinear algebraic equations for a two-point boundary value problems, Jang [26] introduced extended ADM for nonsingular problems with Dirichlet boundary condition. Khuri and Sayfy [27] applied a novel approach based on the mixed decomposition spline for solving singular problems arising in physiology. The method proposed by Ebaid [4] is based on the modification of Lesnic’s work [28]. Later, Duan and Rach [29] introduced special modified inverse linear integral operators for higher order boundary value problem.

To the best of our knowledge, no one has applied ADM to solve a class of doubly singular two-point boundary value problem (1.1) with Types 1 and 2 boundary conditions.

In this work, a new approach based on ADM and new integral operator are proposed for solving doubly singular two-point boundary value problems (1.1) with Types 1 and 2. To set up the modified scheme, we first consider DSBVP (1.1) and use all the boundary conditions and Adomian decomposition method to establish the recursion scheme. Thus a modified recursion scheme is developed which does not require the computation of undermined coefficients, whereas most of previous recursive schemes do require the computation of undermined coefficients (see [23–25]). In fact, the proposed recursion scheme is useful for solving problem (1.1) whether they are linear or nonlinear singular (nonsingular). The main advantage of the method is that it provides a direct scheme for solving the singular boundary value problem, that is, without linearization and discretization. Numerical results are presented to demonstrate the effectiveness of proposed recursive scheme. The symbolic and numerical computations have been performed using “MATHEMATICA” software.

The organization of the paper is as follows. Section 2 presents the inverse integral operator with modified Adomian decomposition method for doubly singular boundary value problems of (1.1) with Types 1 and 2 boundary conditions. In Section 3, the convergence of the method is discussed. In Section 4, we illustrate our method with numerical results along with graphical representation.

2. Modified Adomian Decomposition Method

In this section, we establish two modified recursive schemes for solving doubly singular boundary value problems (1.1) with Types 1 and 2 boundary conditions.

We again write (1.1) with Type 1 boundary conditions as:
()
which can be rewritten as
()
where is the linear differential operator to be inverted and Ny(t) = f(t, y(t)) is an analytic nonlinear operator. It is also assumed that the solution of the problem (2.1) exits and unique. A twofold integral operator L−1(·), regarded as the inverse operator of L(·), is proposed as
()
To establish the recursive scheme, we operate L−1(·) on the left hand side of (2.1) and use initial condition y(0) = a1; we have
()
()
where c2 = p(1)y′(1).
We again operate the inverse operator L−1(·) on both sides of (2.1) and use (2.5), yielding
()
For simplicity, we set and
Then (2.6) can be written as
()
Using the boundary condition y(1) = c1 in (2.7), we get
()
By using c2 into (2.7), we obtain
()
It is important to note that the right hand side of (2.9) does not contain any unknown constants.
The equation (2.9) can be rewritten in the following operator equation form as
()
where
()
Next, the solution y(t) and the nonlinear function Ny(t) are decomposed by infinite series of the form
()
respectively, where An(y0(t), y1(t), …, yn(t)) are Adomian polynomials [19].
Substituting the series (2.12) into (2.9) gives
()
Using the above equation (2.13), the solution components y0, y1, …, yn are determined by the following recursive scheme:
()
We further modify the above algorithm (2.14) to get a more efficient and economic algorithm. To obtain modified algorithm, the zeroth component y0 is divided into the sum of two parts, namely, f0 + f1, where f0 = a1,  f1 = ((c1 − a1)/h(1))h(t). The first part, f0, is kept in y0 and the rest part, f1, is added to y1. Thus, the zeroth component will be y0 = a1 in modified algorithm as
()
Note that new modified recursion scheme (2.15) does not require the computation of undermined coefficients, since this algorithm does not contain any undermined coefficient. This slight change plays a major role for minimizing the size of calculations.
Now, we again consider the same problem (1.1) with Type 2 boundary conditions:
()
which can be rewritten as
()
where is the linear differential operator to be inverted and Ny(t) = f(t, y(t)) is an analytic nonlinear operator. It is also assumed that the solution of problem (2.16) exits and is unique. In this case, we propose the following inverse integral operator:
()
To setup an algorithm, we operate the inverse operator L−1(·) on the left hand side of (2.16) and using the boundary condition y′(0) = 0, we have
()
()
where c0 = y(1).
By operating the inverse operator L−1(·) on both sides of (2.16) and using (2.20) we have
()
Thus (2.21) can be written as
()
Using boundary condition ay(1) + by′(1) = c into (2.22), we obtain
()
The equation (2.23) may be rewritten in operator equation form
()
where
()
Substituting the series (2.12) into (2.23) gives
()
Upon matching both sides of (2.26), the solution components y0, y1, …, yn can be determined by the following modified recursive scheme:
()
Thus, we have established two modified recursive schemes which give the complete determination of solution components yn, and hence the approximate series solution ψn(t) can be obtained for the singular boundary value problems (1.1) with Types 1 and 2 boundary conditions. For numerical purpose, the truncated n-term approximate series solution is given by
()
Note that the truncated n-term approximate series solution is obtained by adding n solutions components y0, y1, …, yn−1, that is, .

3. Convergence of Method

In this section, we discuss the convergence analysis of modified ADM for doubly singular boundary value problem (1.1).

Many authors [30–33] established the convergence of ADM for differential and integral equations. The first proof of convergence of ADM for the general functional equation was given by Cherruault [31]. Cherruault and Adomian [32] proposed a new convergence proof of Adomian decomposition method for the general nonlinear functional equation based on the properties of convergent series. Recently, Hosseini and Nasabzadeh [33] introduced a simple technique to determine the rate of convergence of ADM for initial value problem.

Now, we discuss the convergence of doubly singular two-point boundary value problems (1.1) with Types 1 and 2 boundary conditions. To do so, note that (2.9) and (2.23) may be written in the operator equation form
()
where M is an operator from a Banach space C[0,1] to C[0,1], f is a given function in C[0,1], and we are looking for y ∈ C[0,1] satisfying (3.1).
For Type 1 boundary conditions, we have
()
()
For Type 2 boundary conditions, f and M are given as
()
()
Let the solution y and the nonlinear function Ny be considered as sum of series
()
where An(y0, y1, …, yn) are Adomian polynomials [19].
Substituting the series (3.6) into the operator equation (3.1) yields
()
where
()
for Types 1 and 2 boundary conditions, respectively.
Upon matching both sides of (3.7), we obtain the following scheme:
()
Let be approximate solution, then the modified ADM for (3.1) is equivalent to the following problem:
()
Finding the solution of (3.1) is equivalent to finding the sequence ψn such that ψn = y0 + y1 + ⋯+yn−1 satisfies (3.10).

Theorem 3.1. Let M(y) be the nonlinear operator defined by (3.3) or (3.5) which satisfies the Lipschitz condition ∥M(φ) − M(ξ)∥≤δ∥φ − ξ∥, for all φ, ξ ∈ C[0,1] with Lipschitz constant δ, 0 ≤ δ < 1. If ∥y0∥<∞, then there holds ∥yk+1∥≤δ∥yk∥, for all k ∈ ℕ ∪ {0} and the sequence {ψn} defined by (3.10) converges to .

Proof. Since

()
we have yk+1 = ψk+1 − ψk, k = 1,2, ….

We now show that the sequence {ψn} is convergent. To prove this, it is sufficient to show that {ψn} is cauchy sequence in Banach space C[0,1]. Now using the nonlinearity of M(y), we have

()
Thus we obtain
()
Now for every n, m ∈ ℕ, and n ≥ m, we have
()
As we know is geometric series with common ration δ, 0 ≤ δ < 1. Therefore, we have
()
which converges to zero, that is, ∥ψn − ψm∥→0, as m → ∞. This implies that there exits ψ such that limn→∞ψn = ψ. But, we have , that is, y = ψ which is solution of (3.1). Hence, we have convergence in norm.

4. Numerical Examples and Discussion

In this section, we consider four examples to demonstrate the effectiveness of proposed recursive schemes (2.15) and (2.27). The numerical results are compared with known results and maximum absolute error is also calculated. We also plot approximate and exact solutions to show how approximate solutions converge to exact solution.

Example 4.1. Consider linear two-point boundary value problem [6]

()
with exact solution . For every α > 0 and β > 0, (4.1) is called singular.

In particular, if α = 0.5,  β = 1, that is, p(t) = t0.5 and q(t) = t−0.5 then problem (4.1) is called doubly singular boundary value problem. Applying modified recursive scheme (2.15) to (4.1), the solution components are obtained as
()
For numerical purpose, the approximate series solution is
()
Now, we define error function as En(t) = ψn(t) − y(t) and the maximum absolute errors as
()
For different values of α and β, the maximum absolute error , for n = 4,6, and 8, is shown in Tables 1 and 2, and we observe that when n increases the error decreases. On the other hand, Chawla and Katti [6] applied M3 method based on three evaluations of f to solve the same problem in which a huge amount of computation work is needed to obtain the numerical solution. The results are compared with our approximate series solution in Table 3. Furthermore, the approximate series solutions ψ2,  ψ4 and exact solution y are plotted in Figures 1 and 2. It can be seen from the figures that series solution is very close to exact solution.
Table 1. Maximum error of Example 4.1, when β = 1.
α
0.25 2.3211 × 10−3 4.2210 × 10−5 2.4843 × 10−6
0.5 2.3151 × 10−3 6.1226 × 10−5 3.2320 × 10−6
0.75 3.5315 × 10−3 7.0126 × 10−5 2.2117 × 10−6
Table 2. Maximum error of Example 4.1, when β = 5.
α
0.25 2.2419 × 10−3 3.3304 × 10−5 3.5127 × 10−6
0.5 1.3307 × 10−3 5.0264 × 10−5 4.6572 × 10−6
0.75 4.2104 × 10−3 4.3231 × 10−5 2.1260 × 10−6
Table 3. Maximum error of Example 4.1.
Proposed method Chawla and Katti [6]
α,   β N error
α = 0.50,  β = 4.0 2.4003 × 10−6 128 1.80 × 10−4
α = 0.75,  β = 3.75 5.1431 × 10−6 128 1.80 × 10−4
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Comparison of exact y and approximate ψ2,  ψ4 solutions of Example 4.1, α = 0.50,  β = 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Comparison of exact y and approximate ψ2,  ψ4 solutions of Example 4.1, α = 0.50,  β = 5.

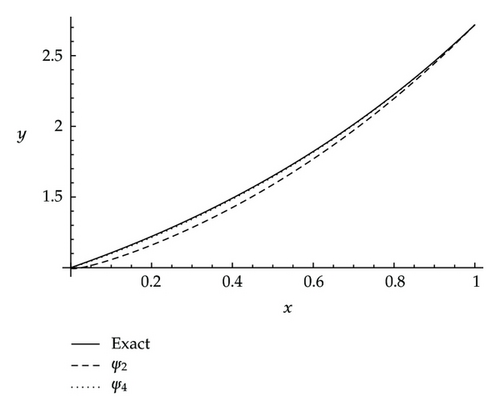
Example 4.2. Consider nonlinear singular two-point boundary value problem

()
with exact solution y(t) = ln(β/(4 + tβ)) and for any real α > 0 and β > 0, this equation is called singular.

If α = 0.25,  β = 1, that is, p(t) = t0.25, q(t) = t−0.75, then problem (4.5) is called doubly singular boundary value problem.

Now we apply recursive scheme (2.15) to obtain the solution components as
()
To compare the results numerically, the 6-term truncated series solution is given by
()
Similarly, for α = 0.5,  β = 1, that is, p(t) = t0.5 and q(t) = t−0.5, the solution components are obtained using the scheme (2.15) as
()
The maximum absolute error , for n = 4,6, and 8, is listed in Tables 4 and 5. As the value of n increases, the maximum absolute error decreases. In addition, to verify how close is our approximate series solutions ψ2,  ψ4 to exact solution y, we have plotted approximate solution and exact solution in Figures 3 and 4. It is shown from figures that the approximate series solution ψ4 is very near to the exact solution y.
Table 4. Maximum error for Example 4.2, when β = 1.
α
0.25 1.3889 × 10−4 2.0435 × 10−6 2.5693 × 10−8
0.5 5.2987 × 10−4 1.1481 × 10−6 1.1616 × 10−8
0.75 2.4545 × 10−4 3.7571 × 10−7 2.1654 × 10−9
Table 5. Maximum error for Example 4.2, when β = 5.
α
0.25 6.5109 × 10−4 2.6137 × 10−7 6.0161 × 10−8
0.5 8.8947 × 10−4 1.1610 × 10−6 7.1746 × 10−8
0.75 7.6596 × 10−4 5.2644 × 10−7 6.3210 × 10−8
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Comparison of exact y and approximate ψ2,  ψ4 solutions of Example 4.2, when α = 0.50,  β = 1.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Comparison of exact y and approximate ψ2,  ψ4 solutions of Example 4.2, when α = 0.50,  β = 5.

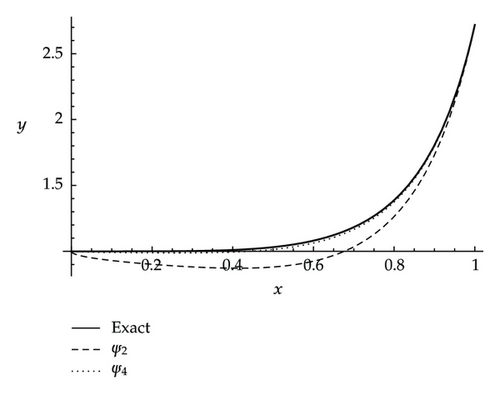
Example 4.3. The heat conduction model in human head problem Duggan and Goodman [13] is

()
We apply the recursive scheme (2.27) to (4.9), where p(t) = q(t) = t2, f = e−y, a = 2, b = 1, and c = 0 then scheme (2.27) for (4.9) becomes as
()

We can easily determine the solution components from above scheme as
()
The truncated series solution ψ8 is obtained by adding y0, y1, …, y6, given by
()
The comparison of numerical results of solutions with known solution is given in Table 6. It can be noted that the approximate solution ψ8 is very close to known solution [13]. However, Duggan and Goodman [13] utilized the maximum principle based on lower and an upper solutions technique in which a lot of calculation is required as we need to solve sequence of linear differential equation analytically.
Table 6. Comparison of numerical results with known results of Example 4.3.
t ψ6 ψ8 ψ10 Solution in [13]
0 0.27073627 0.27025895 0.27010891 0.27035006  
0.2 0.26561546 0.26515412 0.26500927 0.26525434
  0.4 0.25016332 0.24974709 0.24961677 0.24986712  
0.6 0.22410365 0.22375398 0.22364491 0.22388597
  0.8 0.18695255 0.18668071 0.18659620 0.18679895
  1 0.13798246 0.13778979 0.13772998 0.13787263  

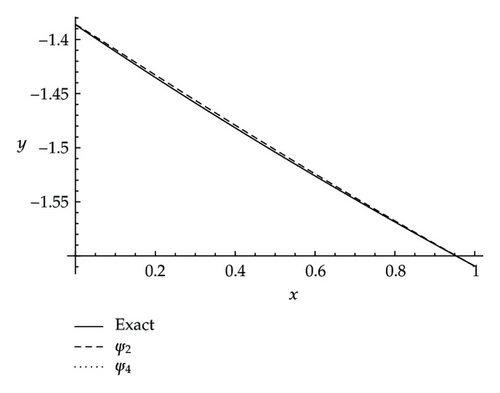
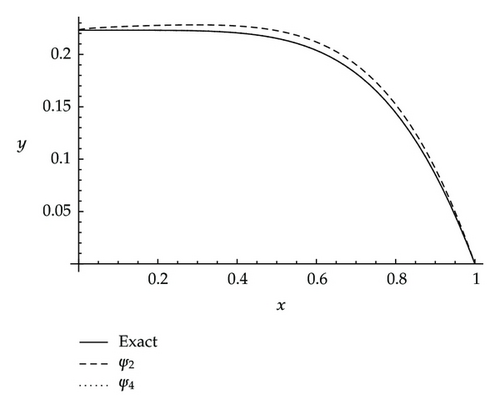
Example 4.4. The nonlinear singular boundary problem considered by Chawla et al. [34] is

()
with exact solution y(t) = 2ln((B + 1)/(Bt2 + 1)), where B = (4 − v − 2(4 − 2v) 1/2)/v, v = 1.

In the above problem, we have p(t) = q(t) = t and f = −ey,  a = 1,  b = 0,  c = 0, by applying recursive scheme (2.27), we have following recursive scheme:
()
We have successive solution components yn as
()
and then the truncated series is obtained as
()
In order to check whether the approximate solution converges to exact solution y, we plot approximate solution ψn, for n = 2,4 and exact solution y in Figure 5. It is clear from the figure that the approximate solution ψ4 converges rapidly to exact solution. The maximum absolute error , for n = 5,8, and 10, is presented in Table 7. It can be noted that Chawla et al. [34] employed fourth-order finite difference method to obtain the numerical solution in which a lot of computation work is required. However, the maximum absolute error obtained was 1.28 × 10−5 using N = 64.
Table 7. Numerical results and maximum error of Example 4.4.
n n Error in [34]
5 6.2129 × 10−4 16 2.52 × 10−3
8 1.0919 × 10−5 32 1.83 × 10−4
10 3.0638 × 10−6 64 1.28 × 10−5
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Comparison of exact y and approximate ψ2,  ψ4 solutions of Example 4.4.

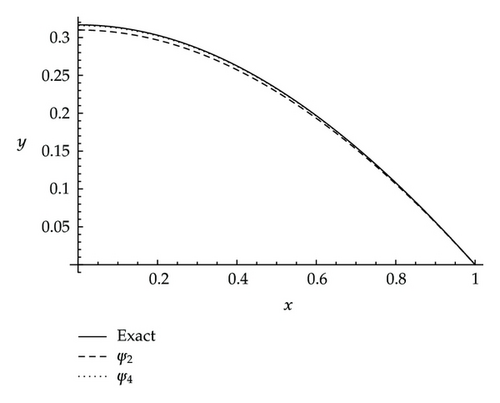
5. Conclusion

In this paper, we we have illustrated how the modified recursive schemes (2.15) and (2.27) can be used to solve a class of doubly singular two-point boundary value problems (1.1) with Types 1 and 2 boundary conditions. The accuracy of the numerical results indicates that the method is well suited for the solution of this type problem. The main advantage of this approach is that it provides a direct scheme to obtain approximate solutions, and we have also shown graphically that these approximate solutions are almost identical to the analytic solution. Another advantage of a modified recursion scheme is that this does not require the computation of undermined coefficients, whereas most of previous recursive schemes do require the computation of undermined coefficients (see [23–25]). The method provides a reliable technique which requires less work compared to the traditional techniques such as finite difference method, Cubic spline method, and standard ADM. The numerical results of the examples are presented and only a few terms are required to obtain accurate solutions. By comparing the results with other existing methods, it has been proved that proposed modified ADM is a more powerful method for solving the singular problems (1.1).

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.