Journal of Applied Mathematics
Volume 2012, Issue 1 538912
Research Article
Open Access

Iterative Algorithms for Solving the System of Mixed Equilibrium Problems, Fixed-Point Problems, and Variational Inclusions with Application to Minimization Problem

Tanom Chamnarnpan, 

Tanom Chamnarnpan

Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangmod, Thrungkru, Bangkok 10140, Thailand kmutt.ac.th

Search for more papers by this author
Poom Kumam, 

Corresponding Author

Poom Kumam

Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangmod, Thrungkru, Bangkok 10140, Thailand kmutt.ac.th

Search for more papers by this author
First published: 01 March 2012
https://doi.org/10.1155/2012/538912
Citations: 2
Academic Editor: Yeong-Cheng Liou

Abstract

We introduce a new iterative algorithm for solving a common solution of the set of solutions of fixed point for an infinite family of nonexpansive mappings, the set of solution of a system of mixed equilibrium problems, and the set of solutions of the variational inclusion for a β-inverse-strongly monotone mapping in a real Hilbert space. We prove that the sequence converges strongly to a common element of the above three sets under some mild conditions. Furthermore, we give a numerical example which supports our main theorem in the last part.

1. Introduction

Let C be a closed convex subset of a real Hilbert space H with the inner product 〈·, ·〉 and the norm ∥·∥. Let F be a bifunction of C × C into ℛ, where ℛ is the set of real numbers, φ : C → ℛ be a real-valued function. Let Λ be arbitrary index set. The system of mixed equilibrium problem is for finding x ∈ C such that
()
The set of solutions of (1.1) is denoted by SMEP(Fk), that is,
()
If Λ is a singleton, then problem (1.1) becomes the following mixed equilibrium problem: finding x ∈ C such that
()
The set of solutions of (1.3) is denoted by MEP (F).
If φ ≡ 0, the problem (1.3) is reduced into the equilibrium problem [1] for finding x ∈ C such that
()
The set of solutions of (1.4) is denoted by EP (F). This problem contains fixed-point problems, includes as special cases numerous problems in physics, optimization, and economics. Some methods have been proposed to solve the system of mixed equilibrium problem and the equilibrium problem, please consult [2–19].
Recall that, a mapping S : C → C is said to be nonexpansive if
()
for all x, y ∈ C. If C is a bounded closed convex and S is a nonexpansive mapping of C into itself, then F(S) is nonempty [20]. Let A : C → H be a mapping, the Hartmann-Stampacchia variational inequality for finding x ∈ C such that
()
The set of solutions of (1.6) is denoted by VI (C, A). The variational inequality has been extensively studied in the literature [21–28].
Iterative methods for nonexpansive mappings have recently been applied to solve convex minimization problems. Convex minimization problems have a great impact and influence on the development of almost all branches of pure and applied sciences. A typical problem is to minimize a quadratic function over the set of the fixed points of a nonexpansive mapping on a real Hilbert space H:
()
where A is a linear bounded operator, F(S) is the fixed point set of a nonexpansive mapping S, and y is a given point in H [29].
We denote weak convergence and strong convergence by notations ⇀ and →, respectively. A mapping A of C into H is called monotone if
()
for all x, y ∈ C. A mapping A of C into H is called α-inverse-strongly monotone if there exists a positive real number α such that
()
for all x, y ∈ C. It is obvious that any α-inverse-strongly monotone mappings A are monotone and Lipschitz continuous mapping. A linear bounded operator A is strongly positive if there exists a constant with the property
()
for all x ∈ H. A self-mapping f : C → C is a contraction on C if there exists a constant α ∈ (0,1) such that
()
for all x, y ∈ C. We use ΠC to denote the collection of all contraction on C. Note that each f ∈ ΠC has a unique fixed point in C.
Let B : H → H be a single-valued nonlinear mapping and M : H → 2H be a set-valued mapping. The variational inclusion problem is to find x ∈ H such that
()
where θ is the zero vector in H. The set of solutions of problem (1.12) is denoted by I(B, M). The variational inclusion has been extensively studied in the literature, see, for example, [30–32] and the reference therein.

A set-valued mapping M : H → 2H is called monotone if for all x, y ∈ H, f ∈ M(x), and g ∈ M(y) impling 〈x − y, f − g〉 ≥ 0. A monotone mapping M is maximal if its graph G(M) : = {(f, x) ∈ H × H : f ∈ M(x)} of M is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping M is maximal if and only if for (x, f) ∈ H × H,   〈x − y, f − g〉 ≥ 0 for all (y, g) ∈ G(M) impling f ∈ M(x).

Let B be an inverse-strongly monotone mapping of C into H, and let NCv be normal cone to C at v ∈ C, that is, NCv = {w ∈ H : 〈v − u, w〉 ≥ 0,   for  all  u ∈ C}, and define
()
Then, T is a maximal monotone and θ ∈ Tv if and only if v ∈ VI (C, B) (see [33]).
Let M : H → 2H be a set-valued maximal monotone mapping, then the single-valued mapping JM,λ : H → H defined by
()
is called the resolvent operator associated with M, where λ is any positive number and I is the identity mapping. It is worth mentioning that the resolvent operator is nonexpansive, 1-inverse-strongly monotone, and that a solution of problem (1.12) is a fixed point of the operator JM,λ(I − λB) for all λ > 0, (for more details see [34]).
In 2000, Moudafi [35] introduced the viscosity approximation method for nonexpansive mappings and proved that if H is a real Hilbert space, the sequence {xn} defined by the iterative method below, with the initial guess x0 ∈ C is chosen arbitrarily,
()
where {αn} ⊂ (0,1) satisfies certain conditions and converges strongly to a fixed point of S (say ), which is then a unique solution of the following variational inequality:
()
In 2006, Marino and Xu [29] introduced a general iterative method for nonexpansive mapping. They defined the sequence {xn} generated by the algorithm x0 ∈ C,
()
where {αn} ⊂ (0,1), and A is a strongly positive linear bounded operator. They proved that if C = H, and the sequence {αn} satisfies appropriate conditions, then the sequence {xn} generated by (1.17) converges strongly to a fixed point of S (say ) which is the unique solution of the following variational inequality:
()
which is the optimality condition for the minimization problem
()
where h is a potential function for γf (i.e., h′(x) = γf(x) for x ∈ H).
For finding a common element of the set of fixed points of nonexpansive mappings and the set of solution of the variational inequalities. Let PC be the projection of H onto C. In 2005, Iiduka and Takahashi [36] introduced the following iterative process for x0 ∈ C,
()
where u ∈ C, {αn} ⊂ (0,1), and {λn} ⊂ [a, b] for some a, b with 0 < a < b < 2β. They proved that under certain appropriate conditions imposed on {αn} and {λn}, the sequence {xn} generated by (1.20) converges strongly to a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality for an inverse-strongly monotone mapping (say ) which solve some variational inequality
()
In 2008, Su et al. [37] introduced the following iterative scheme by the viscosity approximation method in a real Hilbert space: x1, un ∈ H
()
for all n ∈ ℕ, where {αn} ⊂ [0,1) and {rn} ⊂ (0, ∞) satisfing some appropriate conditions. Furthermore, they proved that {xn} and {un} converge strongly to the same point z ∈ F(S)∩VI (C, A)∩EP (F), where z = PF(S)∩VI (C,A)∩EP (F)f(z).
Let {Ti} be an infinite family of nonexpansive mappings of H into itself, and let {λi} be a real sequence such that 0 ≤ λi ≤ 1 for every i ∈ N. For n ≥ 1, we defined a mapping Wn of H into itself as follows:
()
In 2011, He et al. [38] introduced the following iterative process for {Tn : C → C} which is a sequence of nonexpansive mappings. Let {zn} be the sequence defined by
()
The sequence {zn} defined by (1.24) converges strongly to a common element of the set of fixed points of nonexpansive mappings, the set of solutions of the variational inequality, and the generalized equilibrium problem. Recently, Jitpeera and Kumam [39] introduced the following new general iterative method for finding a common element of the set of solutions of fixed point for nonexpansive mappings, the set of solution of generalized mixed equilibrium problems, and the set of solutions of the variational inclusion for a β-inverse-strongly monotone mapping in a real Hilbert space.
In this paper, we modify the iterative methods (1.17), (1.22), and (1.24) by purposing the following new general viscosity iterative method: x0, un ∈ C,
()
for all n ∈ ℕ, where {αn} ⊂ (0,1), {rn} ⊂ (0,2σ), and λ ∈ (0,2β) satisfy some appropriate conditions. The purpose of this paper shows that under some control conditions the sequence {xn} converges strongly to a common element of the set of common fixed points of nonexpansive mappings, the solution of the system of mixed equilibrium problems, and the set of solutions of the variational inclusion in a real Hilbert space. Moreover, we apply our results to the class of strictly pseudocontractive mappings. Finally, we give a numerical example which supports our main theorem in the last part. Our results improve and extend the corresponding results of Marino and Xu [29], Su et al. [37], He et al. [38], and some authors.

2. Preliminaries

Let H be a real Hilbert space and C be a nonempty closed and convex subset of H. Recall that the (nearest point) projection PC from H onto C assigns to each x ∈ H and the unique point in PCx ∈ C satisfies the property
()
which is equivalent to the following inequality
()
The following characterizes the projection PC. We recall some lemmas which will be needed in the rest of this paper.

Lemma 2.1. The function u ∈ C is a solution of the variational inequality if and only if u ∈ C satisfies the relation u = PC(u − λBu) for all λ > 0.

Lemma 2.2. For a given z ∈ H, u ∈ C, u = PCz⇔〈u − z, v − u〉 ≥ 0,   ∀ v ∈ C.

It is well known that PC is a firmly nonexpansive mapping of H onto C and satisfies

()
Moreover, PCx is characterized by the following properties: PCx ∈ C and for all x ∈ H, y ∈ C,
()

Lemma 2.3 (see [40].)Let M : H → 2H be a maximal monotone mapping, and let B : H → H be a monotone and Lipshitz continuous mapping. Then the mapping L = M + B : H → 2H is a maximal monotone mapping.

Lemma 2.4 (see [41].)Each Hilbert space H satisfies Opial′s condition, that is, for any sequence {xn} ⊂ H with xn⇀x, the inequality liminf n→∞∥xn − x∥ < liminf n→∞∥xn − y∥, hold for each y ∈ H with y ≠ x.

Lemma 2.5 (see [42].)Assume {an} is a sequence of nonnegative real numbers such that

()
where {γn} ⊂ (0,1) and {δn} is a sequence in ℛ such that
  • (i)

    ,

  • (ii)

    limsup n→∞δn/γn ≤ 0 or .

Then lim n→∞an = 0.

Lemma 2.6 (see [43].)Let C be a closed convex subset of a real Hilbert space H, and let T : C → C be a nonexpansive mapping. Then I − T is demiclosed at zero, that is,

()
implying x = Tx.

For solving the mixed equilibrium problem, let us assume that the bifunction F : C × C → ℛ and the nonlinear mapping φ : C → ℛ satisfy the following conditions:
  • (A1)

    F(x, x) = 0 for all x ∈ C;

  • (A2)

    F is monotone, that is, F(x, y) + F(y, x) ≤ 0 for any x, y ∈ C;

  • (A3)

    for each fixed y ∈ C, x ↦ F(x, y) is weakly upper semicontinuous;

  • (A4)

    for each fixed x ∈ C, y ↦ F(x, y) is convex and lower semicontinuous;

  • (B1)

    for each x ∈ C and r > 0, there exist a bounded subset Dx⊆C and yx ∈ C such that for any z ∈ C∖Dx,

()
  • (B2)

    C is a bounded set.

Lemma 2.7 (see [44].)Let C be a nonempty closed and convex subset of a real Hilbert space H. Let F : C × C → ℛ be a bifunction mapping satisfying (A1)–(A4), and let φ : C → ℛ be a convex and lower semicontinuous function such that C∩dom φ ≠ ∅. Assume that either (B1) or (B2) holds. For r > 0 and x ∈ H, then there exists u ∈ C such that

()
Define a mapping Kr : H → C as follows:
()
for all x ∈ H. Then, the following hold:
  • (i)

    Kr is single-valued;

  • (ii)

    Kr is firmly nonexpansive, that is, for any x, y ∈ H, ;

  • (iii)

    F(Kr) = MEP (F);

  • (iv)

    MEP (F) is closed and convex.

Lemma 2.8 (see [29].)Assume A is a strongly positive linear bounded operator on a Hilbert space H with coefficient and 0 < ρ ≤ ∥A∥−1, then .

Lemma 2.9 (see [38].)Let C be a nonempty closed and convex subset of a strictly convex Banach space. Let be an infinite family of nonexpansive mappings of C into itself such that ∩i∈NF(Ti) ≠ ∅, and let {λi} be a real sequence such that 0 ≤ λi ≤ b < 1 for every i ∈ N. Then F(W) = ∩i∈NF(Ti) ≠ ∅.

Lemma 2.10 (see [38].)Let C be a nonempty closed and convex subset of a strictly convex Banach space. Let {Ti} be an infinite family of nonexpansive mappings of C into itself, and let {λi} be a real sequence such that 0 ≤ λi ≤ b < 1 for every i ∈ N. Then, for every x ∈ C and k ∈ N, the limit lim n→∞Un,k exist.

In view of the previous lemma, we define

()

3. Strong Convergence Theorems

In this section, we show a strong convergence theorem which solves the problem of finding a common element of the common fixed points, the common solution of a system of mixed equilibrium problems and variational inclusion of inverse-strongly monotone mappings in a Hilbert space.

Theorem 3.1. Let H be a real Hilbert space and C a nonempty close and convex subset of H, and let B be a β-inverse-strongly monotone mapping. Let φ : C → R be a convex and lower semicontinuous function, f : C → C a contraction mapping with coefficient α  (0 < α<1), and M : H → 2H a maximal monotone mapping. Let A be a strongly positive linear bounded operator of H into itself with coefficient . Assume that and λ ∈ (0,2β). Let {Tn} be a family of nonexpansive mappings of H into itself such that

()
Suppose that {xn} is a sequence generated by the following algorithm for x0 ∈ C arbitrarily and
()
for all n = 1,2, 3, …, where
()
and the following conditions are satisfied
  • (C1):

    ;

  • (C2):

    {rn} ⊂ [c, d] with c, d ∈ (0,2σ) and .

Then, the sequence {xn} converges strongly to q ∈ θ, where q = Pθ(γf + I − A)(q) which solves the following variational inequality:

()
which is the optimality condition for the minimization problem
()
where h is a potential function for γf (i.e., h′(q) = γf(q) for q ∈ H).

Proof. For condition (C1), we may assume without loss of generality, and ϵn ∈ (0, ∥A∥−1) for all n. By Lemma 2.8, we have . Next, we will assume that .

Next, we will divide the proof into six steps.

Step 1. First, we will show that {xn} and {un} are bounded. Since B is β-inverse-strongly monotone mappings, we have

()
if 0 < λ < 2β, then I − λB is nonexpansive.

Put yn : = JM,λ(un − λBun), n ≥ 0. Since JM,λ and I − λB are nonexpansive mapping, it follows that

()
By Lemma 2.7, we have
()
and Then, we have
()
Hence, we get
()
From (3.2), we deduce that
()
It follows by induction that
()
Therefore {xn} is bounded, so are {yn}, {Bun}, {f(xn)}, and {AWnyn}.

Step 2. We claim that lim n→∞∥xn+1 − xn∥ = 0 and lim n→∞∥yn+1 − yn∥ = 0. From (3.2), we have

()
Since JM,λ and I − λB are nonexpansive, we also have
()
On the other hand, from and , it follows that
()
()
Substituting y = un into (3.15) and y = un−1 into (3.16), we get
()
From (A2), we obtain
()
so,
()
It follows that
()
Without loss of generality, let us assume that there exists a real number c such that rn−1 > c > 0, for all n ∈ ℕ. Then, we have
()
and hence
()
where M1 = sup {∥un − xn∥ : n ∈ ℕ}. Substituting (3.22) into (3.14), we have
()
Substituting (3.23) into (3.13), we get
()
where M2 = sup {max {∥AWnyn−1∥, ∥f(xn−1)∥ : n ∈ ℕ}}. Since conditions (C1)-(C2) and by Lemma 2.5, we have ∥xn+1 − xn∥ → 0 as n → ∞. From (3.23), we also have ∥yn+1 − yn∥ → 0 as n → ∞.

Step 3. Next, we show that lim n→∞∥Bun − Bq∥ = 0.

For q ∈ θ hence q = JM,λ(q − λBq). By (3.6) and (3.9), we get

()
It follows that
()
So, we obtain
()
where . By conditions (C1), (C3) and lim n→∞∥xn+1 − xn∥ = 0, then, we obtain that ∥Bun − Bq∥ → 0 as n → ∞.

Step 4. We show the following:

  • (i)

    lim n→∞∥xn − un∥ = 0;

  • (ii)

    lim n→∞∥un − yn∥ = 0;

  • (iii)

    lim n→∞∥yn − Wnyn∥ = 0.

Since is firmly nonexpansive and (2.3), we observe that
()
it follows that
()

Since JM,λ is 1-inverse-strongly monotone and by (2.3), we compute

()
which implies that
()
Substituting (3.31) into (3.26), we have
()
Then, we derive
()
By condition (C1), lim n→∞∥xn − xn+1∥ = 0 and lim n→∞∥Bun − Bq∥ = 0.

So, we have ∥xn − un∥ → 0, ∥un − yn∥ → 0 as n → ∞. It follows that

()
From (3.2), we have
()
By condition (C1) and lim n→∞∥yn−1 − yn∥ = 0, we obtain that ∥xn − Wnyn∥ → 0 as n → ∞.

Hence, we have

()
By (3.34) and lim n→∞∥xn − Wnyn∥ = 0, we obtain ∥xn − Wnxn∥ → 0 as n → ∞.

Moreover, we also have

()
By (3.34) and lim n→∞∥xn − Wnyn∥ = 0, we obtain ∥yn − Wnyn∥ → 0 as n → ∞.

Step 5. We show that and limsup n→∞〈(γf − A)q, Wnyn − q〉 ≤ 0. It is easy to see that Pθ(γf + (I − A)) is a contraction of H into itself.

Indeed, since , we have

()
Since H is complete, then there exists a unique fixed point q ∈ H such that q = Pθ(γf + (I − A))(q). By Lemma 2.2, we obtain that 〈(γf − A)q, w − q〉 ≤ 0 for all w ∈ θ.

Next, we show that limsup n→∞〈(γf − A)q, Wnyn − q〉 ≤ 0, where q = Pθ(γf + I − A)(q) is the unique solution of the variational inequality 〈(γf − A)q, w − q〉 ≥ 0 for all w ∈ θ. We can choose a subsequence of {yn} such that

()
As is bounded, there exists a subsequence of which converges weakly to w. We may assume without loss of generality that .

Next we claim that w ∈ θ. Since ∥yn − Wnyn∥ → 0,  ∥xn − Wnxn∥ → 0, and ∥xn − yn∥ → 0, and by Lemma 2.6, we have .

Next, we show that . Since , for k = 1,2, 3, …, N, we know that

()
It follows by (A2) that
()
Hence, for k = 1,2, 3, …, N, we get
()
For t ∈ (0,1] and y ∈ H, let yt = ty + (1 − t)w. From (3.42), we have
()

Since , from (A4) and the weakly lower semicontinuity of φ, and . From (A1) and (A4), we have

()
Dividing by t, we get
()
The weakly lower semicontinuity of φ for k = 1,2, 3, …, N, we get
()
So, we have
()
This implies that .

Lastly, we show that w ∈ I(B, M). In fact, since B is β-inverse strongly monotone, hence B is a monotone and Lipschitz continuous mapping. It follows from Lemma 2.3 that M + B is a maximal monotone. Let (v, g) ∈ G(M + B), since g − Bv ∈ M(v). Again since , we have , that is, . By virtue of the maximal monotonicity of M + B, we have

()
and hence
()
It follows from lim n→∞∥un − yn∥ = 0, we have lim n→∞∥Bun − Byn∥ = 0 and , it follows that
()
It follows from the maximal monotonicity of B + M that θ ∈ (M + B)(w), that is, w ∈ I(B, M). Therefore, w ∈ θ. We observe that
()

Step 6. Finally, we prove xn → q. By using (3.2) and together with Schwarz inequality, we have

()

Since {xn} is bounded, where for all n ≥ 0. It follows that

()
where δn = 2〈Wnyn − q, γf(q) − Aq〉 + ηαn. Since limsup n→∞〈(γf − A)q, Wnyn − q〉 ≤ 0, we get limsup n→∞δn ≤ 0. Applying Lemma 2.5, we can conclude that xn → q. This completes the proof.

Corollary 3.2. Let H be a real Hilbert space and C a nonempty closed and convex subset of H. Let B be β-inverse-strongly monotone and φ : C → ℛ a convex and lower semicontinuous function. Let f : C → C be a contraction with coefficient α  (0 < α < 1), M : H → 2H a maximal monotone mapping, and {Tn} a family of nonexpansive mappings of H into itself such that

()
Suppose that {xn} is a sequence generated by the following algorithm for x0, un ∈ C arbitrarily:
()
for all n = 0,1, 2, …, and the conditions (C1)–(C3) in Theorem 3.1 are satisfied.

Then, the sequence {xn} converges strongly to q ∈ θ, where q = Pθ(f + I)(q) which solves the following variational inequality:

()

Proof. Putting A ≡ I and γ ≡ 1 in Theorem 3.1, we can obtain the desired conclusion immediately.

Corollary 3.3. Let H be a real Hilbert space and C a nonempty closed and convex subset of H. Let B be β-inverse-strongly monotone, φ : C → ℛ a convex and lower semicontinuous function, and M : H → 2H a maximal monotone mapping. Let {Tn} be a family of nonexpansive mappings of H into itself such that

()
Suppose that {xn} is a sequence generated by the following algorithm for x0, u ∈ C and un ∈ C:
()
for all n = 0,1, 2, …, and the conditions (C1)–(C3) in Theorem 3.1 are satisfied.

Then, the sequence {xn} converges strongly to q ∈ θ, where q = Pθ(q) which solves the following variational inequality:

()

Proof. Putting f(x) ≡ u, for all x ∈ C in Corollary 3.2, we can obtain the desired conclusion immediately.

Corollary 3.4. Let H be a real Hilbert space and C a nonempty closed and convex subset of H, and let B be β-inverse-strongly monotone mapping and A a strongly positive linear bounded operator of H into itself with coefficient . Assume that . Let f : C → C be a contraction with coefficient α(0 < α < 1) and {Tn} be a family of nonexpansive mappings of H into itself such that

()
Suppose that {xn} is a sequence generated by the following algorithm for x0 ∈ C arbitrarily:
()
for all n = 0,1, 2, …, and the conditions (C1)–(C3) in Theorem 3.1 are satisfied.

Then, the sequence {xn} converges strongly to q ∈ θ, where q = Pθ(γf + I − A)(q) which solves the following variational inequality:

()

Proof. Taking F ≡ 0, φ ≡ 0,   un = xn, and JM,λ = PC in Theorem 3.1, we can obtain the desired conclusion immediately.

Remark 3.5. Corollary 3.4 generalizes and improves the result of Klin-Eam and Suantai [45].

4. Applications

In this section, we apply the iterative scheme (1.25) for finding a common fixed point of nonexpansive mapping and strictly pseudocontractive mapping.

Definition 4.1. A mapping S : C → C is called a strictly pseudocontraction if there exists a constant 0 ≤ κ < 1 such that

()
If κ = 0, then S is nonexpansive. In this case, we say that S : C → C is a κ-strictly pseudocontraction. Putting B = I − S. Then, we have
()
Observe that
()
Hence, we obtain
()
Then, B is a ((1 − κ)/2)-inverse-strongly monotone mapping.

Using Theorem 3.1, we first prove a strongly convergence theorem for finding a common fixed point of a nonexpansive mapping and a strictly pseudocontraction.

Theorem 4.2. Let H be a real Hilbert space and C a nonempty closed and convex subset of H, and let B be an β-inverse-strongly monotone, φ : C → ℛ a convex and lower semicontinuous function, and f : C → C a contraction with coefficient α  (0 < α < 1), and let A be a strongly positive linear bounded operator of H into itself with coefficient . Assume that . Let {Tn} be a family of nonexpansive mappings of H into itself, and let S be a κ-strictly pseudocontraction of C into itself such that

()
Suppose that {xn} is a sequence generated by the following algorithm for x0, un ∈ C arbitrarily:
()
for all n = 0,1, 2, …, and the conditions (C1)–(C3) in Theorem 3.1 are satisfied.

Then, the sequence {xn} converges strongly to q ∈ θ, where q = Pθ(γf + I − A)(q) which solves the following variational inequality:

()
which is the optimality condition for the minimization problem
()
where h is a potential function for γf (i.e., h′(q) = γf(q) for q ∈ H).

Proof. Put B ≡ I − T, then B is (1 − κ)/2 inverse-strongly monotone and F(S) = I(B, M), and JM,λ(xn − λBxn) = (1 − λ)xn + λTxn. So by Theorem 3.1, we obtain the desired result.

Corollary 4.3. Let H be a real Hilbert space and C a closed convex subset of H, and let B be β-inverse-strongly monotone and φ : C → ℛ a convex and lower semicontinuous function. Let f : C → C be a contraction with coefficient α  (0 < α < 1) and Tn a nonexpansive mapping of H into itself, and let S be a κ-strictly pseudocontraction of C into itself such that

()
Suppose that {xn} is a sequence generated by the following algorithm for x0 ∈ C arbitrarily:
()
for all n = 0,1, 2, …, and the conditions (C1)–(C3) in Theorem 3.1 are satisfied.

Then, the sequence {xn} converges strongly to q ∈ θ, where q = Pθ(f + I)(q) which solves the following variational inequality:

()
which is the optimality condition for the minimization problem
()
where h is a potential function for γf (i.e., h′(q) = γf(q) for q ∈ H).

Proof. Put A ≡ I and γ ≡ 1 in Theorem 4.2, we obtain the desired result.

5. Numerical Example

Now, we give a real numerical example in which the condition satisfies the ones of Theorem 3.1 and some numerical experiment results to explain the main result Theorem 3.1 as follows.

Example 5.1. Let H = R, C = [−1,1], Tn = I, λn = β ∈ (0,1), n ∈ N, Fk(x, y) = 0, for all x, y ∈ C, rn,n = 1, k ∈ {1,2, 3, …, N}, φ(x) = 0, for all x ∈ C, B = A = I, f(x) = (1/5)x, for all x ∈ H, λ = 1/2 with contraction coefficient α = 1/10, ϵn = 1/n for every n∈N, and γ = 1. Then {xn} is the sequence generated by

()
and xn → 0 as n → ∞, where 0 is the unique solution of the minimization problem
()

Proof. We prove Example 5.1 by Step 1, Step 2, and Step 3. By Step 4, we give two numerical experiment results which can directly explain that the sequence {xn} strongly converges to 0.

Step 1. We show

()
where
()

Indeed, since Fk(x, y) = 0 for all x, y ∈ C,   n ∈ {1,2, 3, …, N}, due to the definition of Kr(x), for all x ∈ H, as Lemma 2.7, we have

()

Also by the equivalent property (2.2) of the nearest projection PC from H → C, we obtain this conclusion, when we take x ∈ C, . By (iii) in Lemma 2.7, we have

()

Step 2. We show that

()

Indeed. By (1.23), we have

()

Computing in this way by (1.23), we obtain

()

Since Tn = I, λn = β, n ∈ N, thus

()

Step 3. We show that

()
where 0 is the unique solution of the minimization problem
()

Indeed, we can see that A = I is a strongly position bounded linear operator with coefficient is a real number such that , so we can take γ = 1. Due to (5.1), (5.4), and (5.7), we can obtain a special sequence {xn} of (3.2) in Theorem 3.1 as follows:

()
Since Tn = I, n ∈ N, so,
()
combining with (5.6), we have
()

By Lemma 2.5, it is obviously that zn → 0, 0 is the unique solution of the minimization problem

()
where q is a constant number.

Step 4. We give the numerical experiment results using software Mathlab 7.0 and get Table 1 to Table 2, which show that the iteration process of the sequence {xn} is a monotone-decreasing sequence and converges to 0, but the more the iteration steps are, the more showily the sequence {xn} converges to 0.

Table 1. This table shows the value of sequence {xn} on each iteration step (initial value x1 = 1).
n xn n xn
1 1.000000000000000 31 0.000000000054337
2 0.200000000000000 32 0.000000000026643
3 0.070000000000000 33 0.000000000013072
4 0.028000000000000 34 0.000000000006417
⋮ ⋮ ⋮ ⋮
19 0.000000301580666 39 0.000000000000184
20 0.000000146028533 40 0.000000000000091
21 0.000000070823839 41 0.000000000000045
⋮ ⋮ ⋮ ⋮
29 0.000000000226469 47 0.000000000000001
30 0.000000000110892 48 0.000000000000000
Table 2. This table shows the value of sequence {xn} on each iteration step (initial value x1 = 1/2).
n xn n xn
1 0.500000000000000 31 0.000000000027168
2 0.100000000000000 32 0.000000000013321
3 0.035000000000000 33 0.000000000006536
4 0.014000000000000 34 0.000000000003208
⋮ ⋮ ⋮ ⋮
19 0.000000150790333 39 0.000000000000092
20 0.000000073014267 40 0.000000000000045
21 0.000000035411919 41 0.000000000000022
⋮ ⋮ ⋮ ⋮
29 0.000000000113235 46 0.000000000000001
30 0.000000000055446 47 0.000000000000000

Now, we turn to realizing (3.2) for approximating a fixed point of T. We take the initial valued x1 = 1 and x1 = 1/2, respectively. All the numerical results are given in Tables 1 and 2. The corresponding graph appears in Figures 1(a) and 1(b).

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
The iteration comparison chart of different initial values. (a) x1 = 1 and (b) x1 = 1/2.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
The iteration comparison chart of different initial values. (a) x1 = 1 and (b) x1 = 1/2.

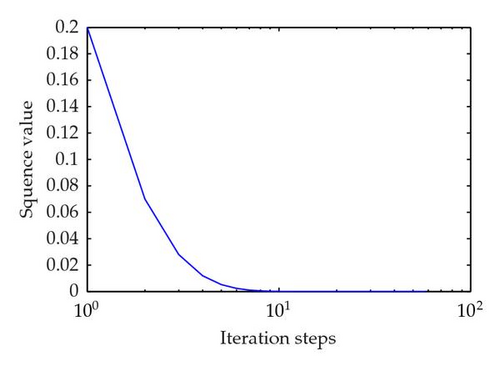
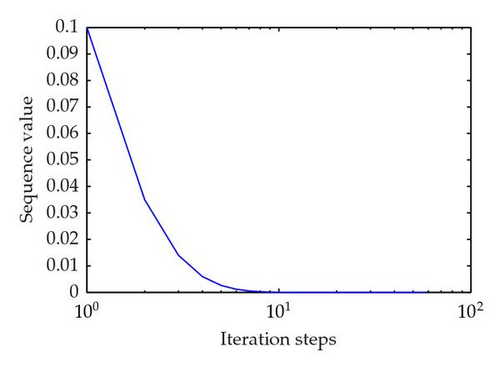
The numerical results support our main theorem as shown by calculating and plotting graphs using Matlab 7.11.0.

Acknowledgments

The authors would like to thank the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission (under the project NRU-CSEC no. 54000267) for financial support. Furthermore, the second author was supported by the Commission on Higher Education, the Thailand Research Fund, and the King Mongkut′s University of Technology Thonburi (KMUTT) (Grant no. MRG5360044). Finally, the authors would like to thank the referees for reading this paper carefully, providing valuable suggestions and comments, and pointing out major errors in the original version of this paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.