Mathematical Analysis of Inclusion Removal from Liquid Steel by Gas Bubbling in a Casting Tundish
Abstract
The mechanism of inclusion removal from liquid steel by gas bubbling and bubble attachment in the tundish is complex due to the great number of variables involved, and it is even more difficult to study because of the turbulent flow conditions. The main objective of this work is to analyze and improve the understanding of the alumina inclusion removal rate by bubble attachment and by gas bubbling fluid dynamics effects. The results show that the inclusion collection probability mainly depends on the attachment mechanism by collision. This parameter was determined by calculating the induction time, which is shorter when the rupture time and the formation time of a stable three phases contact (particle/liquid/gas) are ignored than when it is fully considered, affecting the attachment probability. In addition, to achieve acceptable inclusion removal, a smaller bubble diameter is required, such as 1 mm. This consideration is almost impossible to achieve during tundish operation; a more realistic bubble diameter around 10 mm is employed, resulting in a very inefficient inclusion removal process by bubble attachment. Nevertheless, in a real casting tundish the inclusion removal rate employing argon bubbling is efficient; is mainly due to the fluid flow pattern changes rather than bubble attachment. Consequently, it is imperative to consider the summation of both removal mechanisms to compute a better approximation of this important operation.
1. Introduction
Due to the stringent control on the cleanliness of the steel, many steel casting shops around the world have studied extensively the tundish systems employed, not only to maximize the benefits of increasing the residence time by flow control and reduce contamination, but also to have better and faster assimilation of the non metallic inclusions by the slag. The most recent research reported in the open literature on the subject of inclusion removal in tundish can be grouped in three main subjects: the effect of the fluidynamics on the inclusion trajectories [1–5], the mechanisms of inclusions assimilation by the slag [6, 7], and the mechanisms of inclusion removal by bubble flotation [4, 8–28].
Argon bubbling is a very attractive technology used as a flow control and inclusion removal, it strongly affects the fluid flow patterns in the tundish by reducing the dead flow zones and by increasing the plug flow together with the mean residence time [22–24, 27]. In addition, it has been found by industrial trial that the implementation of this operation improves the inclusion removal rate by decreasing the final range of inclusion size, and the inclusion ratio in the final product [25, 28]. Furthermore, there are some works focusing on the main variables that control the particle-bubble flotation mechanisms [16–19]. Even with all this research, there is a gap in the knowledge of the inclusion-bubble interaction in the tundish and its effect on the removal rate. A few efforts have been done to study this subject, such as the work done by Rogler et al. [20], where the porous zone width effect on the inclusion removal in the tundish was studied. However, in this work many assumptions were taken, for instance considering constant the collection probability. Another important effort was developed by Zhang and Taniguchi [4] where the silica inclusion removal by bubble flotation in the ladle was determined by using the oscillation model.
Equally important is to consider the detrimental effect of the submerged entry nozzle clogging by alumina inclusions in the tundish and the limited understanding on the subject. Therefore, the objective of this work is to analyze mathematically and analytically the alumina inclusion removal rate before they get to the submerge entry nozzle by bubble attachment mechanism, considering attachment by oscillation or sliding models and the collection probability as a function of complete induction time, and by the bubbling fluidynamic effects.
2. Model Development
A fluidynamics mathematical model was developed based on a previous published work by the authors [9] and an analytical model was developed to understand the attachment mechanism for inclusion removal in the tundish. The fundamental equations and mechanisms are described as follows.
2.1. Mechanisms for Particle-Bubble Interaction
- (1)
inclusion approximation to the bubble;
- (2)
liquid film formation between inclusion and bubble;
- (3)
oscillation or sliding of the inclusion on the bubble surface;
- (4)
drainage and rupture of the film to achieve the three phase contact (TPC);
- (5)
stabilization of the system particle-bubble against external stresses;
- (6)
flotation of the stable system inclusion-bubble.
This mechanism is influenced by many parameters, where the system is very sensitive. Those parameters are as follows.
The induction time is a relatively new parameter that has not been fully studied.
2.2. Inclusion Collection Probability
2.3. Mathematical Model Considerations and Boundary Conditions
The fluidynamic model consists-of the fundamental Navier-Stokes equations, together with the k-ε turbulence model and the discrete phase model [9] embedded in the commercial CFD code FLUENT. The liquid steel flowing in the tundish is assumed to have Newtonian behavior, under isothermal and steady state conditions. Both turbulent and laminar flows coexist in the tundish; however, only laminar flow is present close to solid walls. Consequently, typical nonslipping conditions were applied to all solid surfaces. Wall functions were used at the nodes close to any wall. The gravity force was considered to act over the y-coordinate. No slag layer was considered, instead a plane surface was assumed where the velocity gradients, turbulent kinetic energy, and its dissipation rate are taken as zero.
To study the macroscopic flow effect, the simulated inclusions were assumed to have a spherical rigid shape with the physical properties of alumina. No interaction among the inclusions was considered; therefore, agglomeration and collision were not simulated. The only inclusion removal mechanism considered was Stoke’s flotation. Inclusion trajectories were calculated using a Langrangian particle-tracking approach, which solves a transport equation for each inclusion as they travel through the previous calculated velocity field of liquid steel. This approach assumes that the interaction between steel and the inclusion is one-way coupled, that is, only the steel affects the trajectories of inclusions but these do not affect the steel flow. The boundary conditions for inclusion removal were as follows: any inclusion that reached the free surface was considered removed and the rest was considered as escaped.
2.4. Analytical Model Description and Considerations
The argon bubbles have a constant size, and they are uniformly distributed in the bubble region. The bubble-bubble and inclusion-inclusion interactions are ignored. The inclusion-inclusion collision as well as the agglomeration is not considered, and the inclusion size does not affect the bubble trajectory. The removal mechanisms considered are bubble flotation and buoyancy forces.
For the calculation of the inclusion removal rate by bubble attachment, five main programs were developed, for those the dimensionless constants (A, B, C, D, X, Y all these constants were calculated with the equations proposed by Nguyen et al. [17, 18]) were calculated as a function of the Reb. Program I: calculate db, ub, ti, Pa, Pc, E ri , tc, t fr , hcrit using small increments of the gas flow rate and the diameter of the pore in the porous plug. Program II: calculate up, Pc, Pa, E ri , tc, ti, t fr , hcri using different width of the bubble region, but considering constant the resident time of the steel, the bubble diameter, the gas flow rate, and the diameter of the pore in the porous region. Program III: calculate Pc, Pa, tc, t fr , hcrit using constant the inclusion diameter and the bubble diameter. Program IV: calculate db, ub, Pa, Pc, E ri , tc, t fr , hcrit but employing constant the gas flow rate and the diameter of the pore in the porous plug. Program V: calculate P, Pa, Pc, ts, tc, t fr , ti, hcrit for different bubble and inclusion diameters. This has been summarized in Table 1.
| Program | Variables calculated | Parameters modified | Equation numbers employed | Dimensionless constants |
|---|---|---|---|---|
| I | db, ub, Pa, Pc, Eri , ti, tc, tfr, hcrit | dp, n0, τ, d0, Qg | 1, 2, 3, 5, 6, 7, 9, 10, 11 | A, B, C, D, X, Y |
| II | up, Pc, Pa, Eri , tc, tfr, ti, hcri | dp, n0, τ, d0, Qg, db | 1, 2, 3, 5, 7, 9, 10, 11 | A, B, C, D, X, Y |
| III | Pc, Pa, tc, tfr, hcrit | dp, db | 1, 2, 3, 10, 11 | C, D, X, Y |
| IV | db, ub, Pa, Pc, Eri , tc, tfr, hcrit | dp, n0, d0, Qg | 1, 2, 3, 6, 7, 9, 10, 11 | A, B, C, D, X, Y |
| V | P, Pa, Pc, ts, tc, tfr, ti, hcrit | dp, db | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11 | A, B, C, D, X, Y |
3. Results and Discussion
3.1. Analytical Analysis
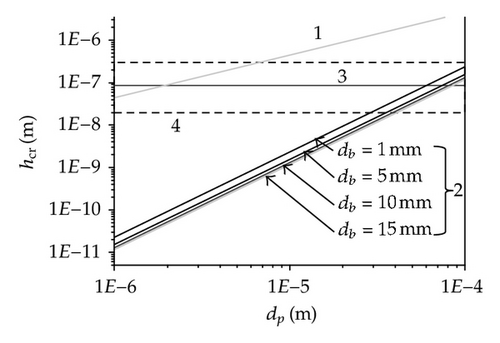
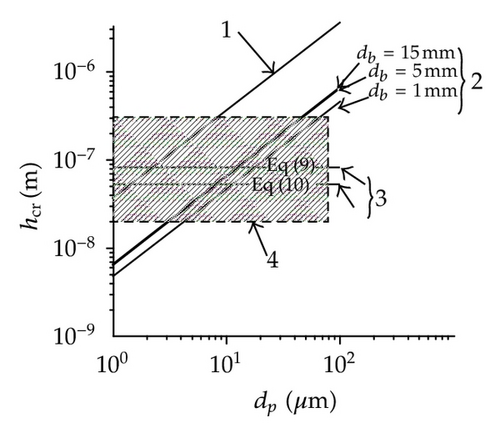
The first variable calculated was the Critical Film Thickness (hcr) for alumina inclusions, this variable was predicted using the hole formation and oscillation models, and the Schulze and Birzer empirical relationship. The results are shown in Figure 1(a), where hcr for this inclusion type has values between 0.015–452 nm. Consequently, the dominant forces for the film draining and rupture are the Van der Waals forces. It was also observed that hcr value is bigger when it is calculated using the hole formation model indicating that the liquid film rupture takes place easier by the formation of a hole. Since this work is focused on inclusion sizes ranging between 1–40 microns, it can be observed that the predicted values for hcr are in the zone of the experimental results in water systems. Furthermore, Figure 1(b) shows the hcr results for silica inclusions reported by Zhang and Taniguchi [4], who established that hcr value is 3 to 5 times higher for the hole formation model than the values obtained by oscillation model, concluding that the film rupture is easier by the formation of a hole. These authors suggested that for alumina inclusions the film drainage and rupture may occur by the formation of a hole, which is corroborated by the present results and it was concluded that hcr is dependent of the inclusion type, and the film rupture will take place by the hole formation mechanism, which will be the model to be considered further on.
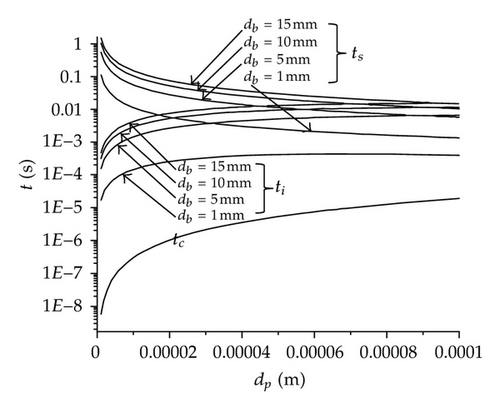
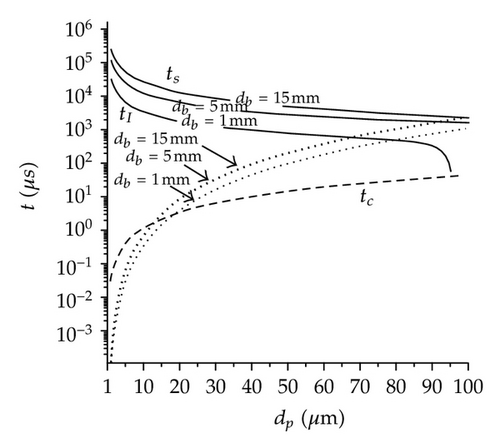
It is well known that the inclusion attachment mechanisms to a bubble can be by collision or by sliding. For such reason, it is required to know the collision time (tc), the sliding time (ts), and the induction time (ti), since the controlling attachment mechanism is determined through these three variables. The induction time is the time required to achieve the drainage and rupture of the film, in order to reach a stable three phase contact (TPC). In previous research works, some of the considerations were taken to predict the induction time results in smaller values, for instance, Wang et al. [14] calculated ti = tfc without considering TPC rupture time and the time for the formation of the stable TPC; however, the authors advice that this assumption is not exact; this hypothesis was also considered by Rogler et al. [20]. Nevertheless, due to its importance, in the present work it has been fully calculated using Nguyen’s model (2.7). The numerical values of these three time variables calculated for alumina inclusions are shown in Figure 2(a). Where it should be taken into account that if tc > ti, the inclusion attachment is by collision if tc < ti, the inclusion does not attach if ts > ti, the inclusion attachment is by sliding and if ts < ti the inclusion slide; but it does not attach. Considering this as a reference, the results show that in general ti > tc for the studied bubble diameters; consequently, the alumina inclusion attachment occurs by sliding or bouncing back, but it will not take place by collision. About the variable ts when the bubble size is 1 mm ts > ti, meaning that the inclusion attaches by sliding, and when the bubbles size is 5 mm ts > ti but only for particles diameters up to 83 μm. Figure 2(a) also shows the limit for inclusion diameter that may attach to a bubble, which is identified by the intersecting point of ts and ti. The present results show bigger ti values and therefore smaller limits compared to those obtained previously by Zhang and Taniguchi [13]. Therefore, it is essential to select adequately the model used for compute ti.
To predict the inclusion removal rate in the tundish, it is required the collection probability which depends on the attachment and collision probabilities; for this reason, these probabilities are first analyzed. Figure 3(a) shows the calculated Patt values as a function of the bubble and particle diameters, where it can be seen that for dp < 10 microns the values obtained are close to unity, independently of the db. This indicates that any inclusion that impacts a bubble will be removed. On the other hand, for dp > 10 microns the Patt becomes a function of db, for example for db = 1 mm the Patt is high; nevertheless, for db = 5 mm the Patt decreases exponentially. Moreover, for bigger bubble diameters such as 10 or 15 mm, the Patt shows values and a declined profile similar to db = 5 mm. These results are in accordance to previous works published in the open literature [13, 14, 20], which means that the present model predicts correctly the Patt and allows to conclude that it is necessary to have db < 5 mm to remove efficiently small alumina inclusions in the range of 1–40 microns.
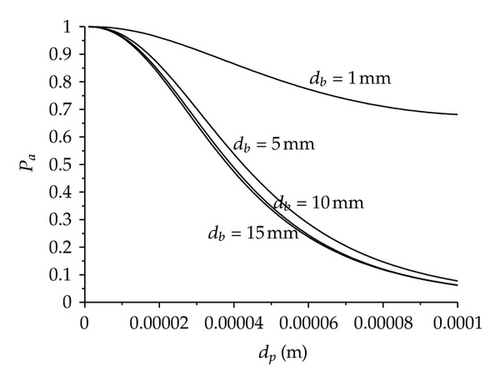
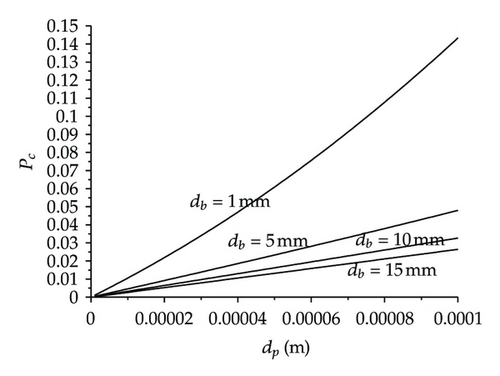
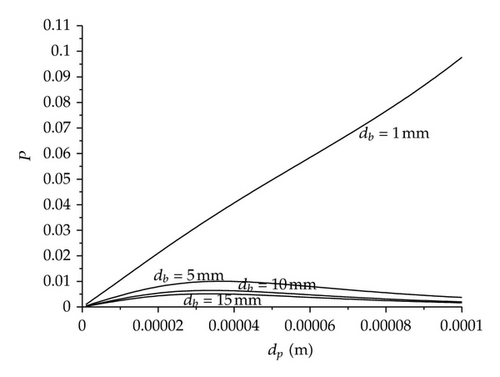
Figure 3(b) shows that, in general, the collision probability is very low independently of the bubble and inclusion sizes. It is important to state that if an inclusion collides with a bubble, the removal probability will be high. In order to improve the collision probability considering the above inclusion size range, it is required that bubble diameters be smaller than 1 mm. However, in the liquid steel flowing inside the tundish it is extremely difficult to get argon bubble diameters as small as 1 mm; therefore, the Pc will be very low and consequently the collection probability will be even smaller, this can be observed in Figure 4. Taken into consideration the calculated information, the inclusion removal rate in the tundish by bubble attachment may not be as efficient as can be expected and it is perhaps more dependent on other variables. According to this hypothesis, it is required to calculate the inclusion removal rate (RE) of a typical two-strand tundish. To determin this variable, it was necessary to define some parameters, such as the width of the porous media considering both sides (LB), the tundish mean residence time (TR) and the mean residence time inside the bubble zone (TRB); the last two are directly related with the steel level which was set as constant implicating that TR is constant, and TRB depends only on the LB variable. With these conditions, RE was calculated using the Rogler and Heaslip model [20] and the results are shown in Figure 5(a). In this figure, the requirement of small bubble diameters to get an efficient inclusion removal is evident once more. Through these results the declared hypothesis in Figure 4 is confirmed, since RE values are smaller than 30% for inclusion in the interest range with 10 mm argon bubble diameter.
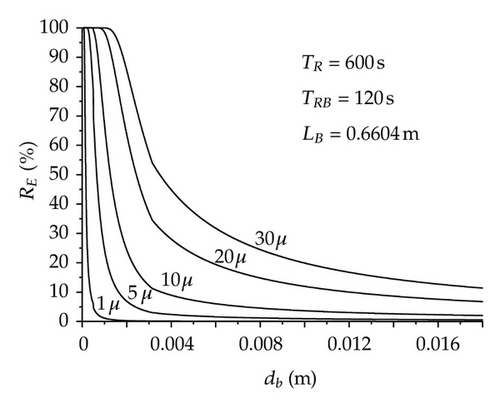
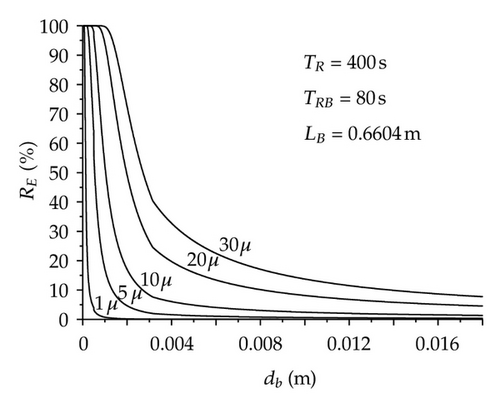
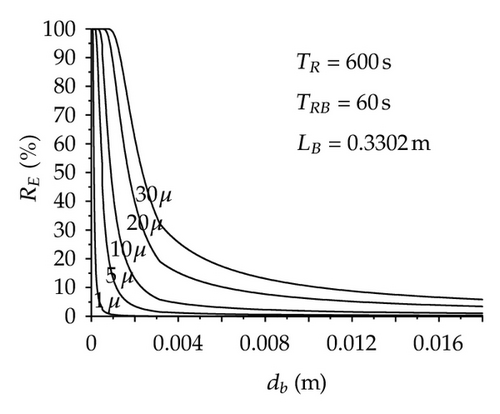
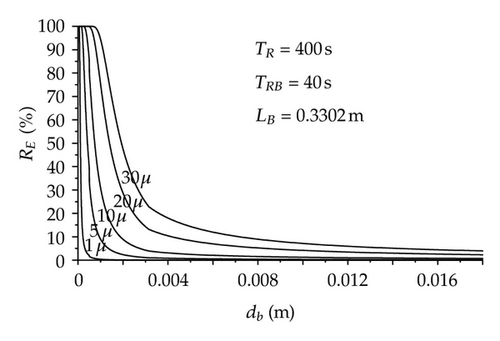
In spite of the small values mentioned above, it is necessary to find out the controlling variable on RE. In order to achieve this goal, some variations were considered and their effects were analyzed against the RE value of 21% for dp = 30 microns and bd = 10 mm. First, the TR was decreased from 600 to 400 seconds, Figure 5(b). This change turned out in a 33% decrease of TRB, consequently a 34% decrease of RE reference value was observed. Second, reducing by half LB and keeping TR constant, Figure 5(c), the TRB value was diminished to 50% causing a drop of 52% on RE. Finally, the two previous reductions were put together, Figure 5(d), and resulted in a TRB decrease of 66% inducing an RE value of 6%. According to these results, RE is a direct function of TRB. As in the majority of the tundish systems LB, TR, and TRB are constants, RE depends exclusively on the bubble attachment mechanism which is a very inefficient process as has been shown above. However, to explain the benefices reported from other modelling studies [8, 9, 26] and those observed in practice [8, 28], where the argon bubbling helps a lot the inclusion removal, it is necessary to consider additionally the fluidynamics analysis of the system. This need is focused in the strong modification of the flow patterns produced by the argon bubbling; first of all, the bubble curtain redirects the flow towards the free surface, and secondly, the leaving flow from the curtain shows a plug behavior promoting a bigger inclusion uncoupling. As a consequence of these patterns, it is possible to obtain a considerable improvement on the inclusion removal.
3.2. Mathematical Analysis
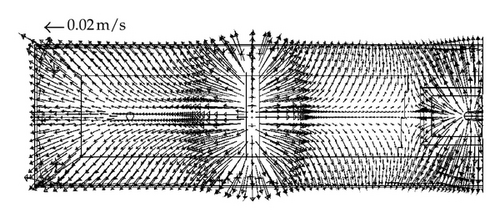
In order to confirm the last hypothesis, a mathematical simulation of the fluidynamics in a tundish equipped with a turbulence inhibitor and under argon bubbling was carried out, in which RE was only calculated by fluidynamics effects (Stoke’s flotation). Since there are many different tundish configurations, it was considered a typical slab tundish configuration and the numerical assumptions employed in a previous published work [9]. The characteristic dimensions of the tundish and the mesh used in this study are presented in Figure 6.
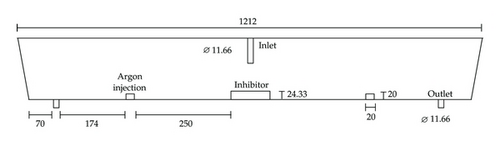

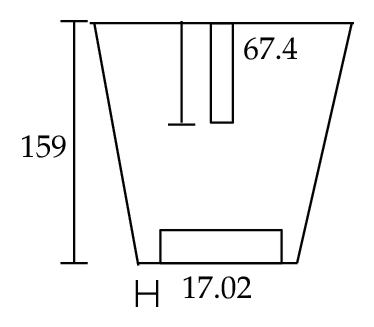

It should be taken into account that the inclusions are only removed when they reach the free surface; consequently, when the movement of the steel towards the free surface is acquired, a better removal percentage can be expected. It is important to notice that RE could be anticipated to be bigger than the one calculated by attachment since the area of removal is also bigger; due to the difference of densities the uncoupling mechanism is easier than the bubble attachment mechanism.
Observing the flow pattern changes in Figures 7 and 8, it can be seen that when argon is not injected, the fluid flow is directed by the turbulence inhibitor towards the free surface inducing a better removal efficiency since it promotes a redirection of the inclusion to the steel-slag interface. However, nearly at half of the distance between the inlet and the outlet, the steel moves downwards; this change has as a consequence that the inclusions move far from the interface, because of that, most of the inclusions are removed mainly at the first half of the tundish. Nevertheless, when the argon is injected, the flow patterns have a strong change since two recirculation patterns are produced before and after the argon bubbling zone. These two changes generate a major removal percentage of inclusion due to the recirculation patterns.
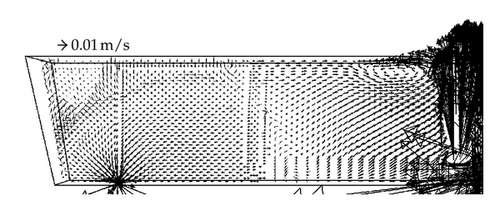
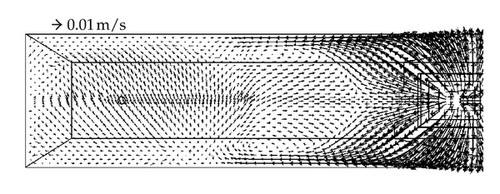
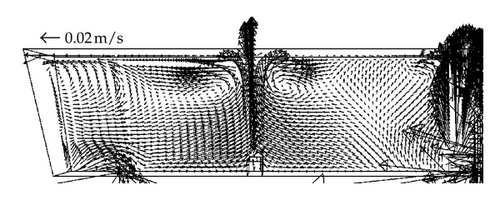
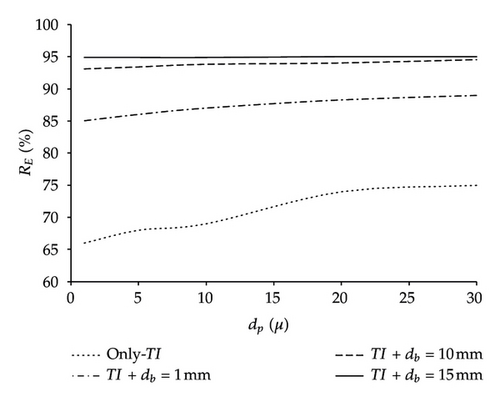
For this study, the alumina inclusions were fed in the tundish entry nozzle and it was considered that the removed inclusions were only those that reach the tundish steel-slag interface. Since the most difficult inclusion removal size are those smaller than 30 microns, the results for that range are shown in Figure 9, where it can be observed that without argon, bubbling RE is near to 70% only by fluid flow. Now, if it is considered argon injection with db = 1 mm, RE is improved by a further 15% just for fluidynamics, even more, if we add the theoretical RE by bubble attachment (Figure 5(a)) the total RE should be close to 100%. Nevertheless, for more regular bubble diameters such as db = 10 mm or bigger like 15 mm, the bubble curtain effects on steel movement is larger inducing a major displacement of the fluid to the interface steel-slag; consequently, RE must increase as actually is happening since RE achieves values close to 90%. Thus, even RE by bubble attachment is quite low (near to 21%), the total RE should be bigger than 90%. It is important to notice that the total RE is not only a direct sum of both percentages. Figure 10 shows the combination of the two mechanisms and shows the increasing of the total RE.
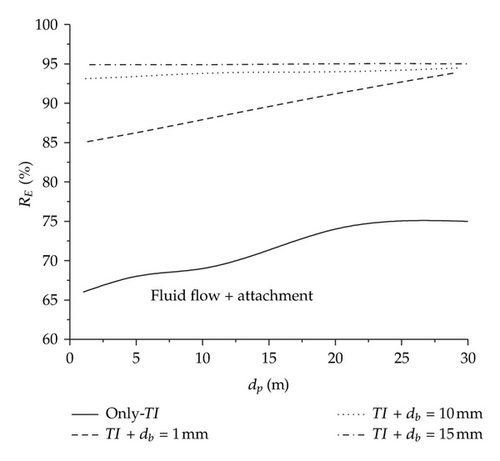
With these results it can be concluded that the inclusion removal rate in the tundish is efficient, employing argon bubbling mainly by the fluid flow pattern changes rather than by bubble attachment. Additionally, it can be established that it is imperative to consider the summation of both removal mechanisms to compute a better approximation of this important operation.
Finally, it is important to mention that these higher values of RE are a close approximation, since many of the inclusions that reach the interface never get absorbed by the slag and some others get back to the steel flow again, due to the strong turbulence of the liquid steel; consequently, this removal percentage is a powerful indicative of the way a tundish reactor is working on the inclusion removal, but until now it still impossible to establish that these results are definitive.
4. Conclusions
- (1)
The results show that the film rupture between the inclusion and the bubble is easier by the formation of a hole and this mechanism has a dependency of the inclusion type.
- (2)
Since the current results show bigger ti values, this work demonstrates that the model used to calculate ti is important and as a consequence smaller attachment limits are obtained. At the same time, these increased values of ti turn out in smaller percentage of the alumina inclusion collection probability.
- (3)
The removal rate (RE) shows more dependency on other variables such as TR and LB; those variables show an indirect effect on RE since it affects directly TRB, which represents the controlling variable on the inclusion removal by bubble attachment.
- (4)
The results indicate that it is required to have very small bubble diameters to achieve acceptable RE percentages, however, in the real process, this consideration is almost impossible to get, and the real bubble diameters are around 10 mm resulting in a very inefficient inclusion removal process in the tundish by bubble attachment.
- (5)
Despite of conclusion four, the inclusion removal rate in the tundish is efficient employing argon bubbling, mainly by the fluid flow patterns changes rather than by bubble attachment. Then, it can be established that is imperative to consider the summation of both removal mechanisms, to compute a better approximation of this important operation.
Nomenclature
-
- A :
-
- Dimensionless parameters which are functions of the Reynolds bubble
-
- B:
-
- Dimensionless parameters which are functions of the Reynolds bubble
-
- C:
-
- Dimensionless parameters which are functions of the Reynolds bubble
-
- D:
-
- Dimensionless parameters which are functions of the Reynolds bubble
-
- dp:
-
- Particle diameter
-
- db:
-
- Bubble diameter
-
- d0:
-
- Porous diameter
-
- g:
-
- Gravity
-
- h crit:
-
- Critical film thickness
-
- k:
-
- Shape factor = 4
-
- no:
-
- Initial inclusion concentration
-
- n:
-
- Inclusion concentration
-
- N Re,O:
-
- Reynolds bubble
-
- P:
-
- Collection probability
-
- P att:
-
- Attachment probability
-
- Pc:
-
- Collision probability
-
- Pdet:
-
- Detachment probability
-
- Qg:
-
- Gas flow rate
-
- RE:
-
- Inclusion removal rate
-
- ti:
-
- Induction time
-
- tc:
-
- Collision time
-
- t fr :
-
- Drainage time
-
- ts:
-
- Sliding time
-
- t fc :
-
- Film drainage and rupture time during collision
-
- TF:
-
- Steel temperature (1800 K)
-
- T0:
-
- Gas temperature (300 K)
-
- up:
-
- Particle velocity
-
- uB:
-
- Bubble velocity.
Greek symbols
-
- ρp:
-
- Particle density
-
- ρg:
-
- Gas density
-
- σL:
-
- Superficial tension
-
- μL:
-
- Liquid viscosity
-
- θ:
-
- Polar angle
-
- θc:
-
- Polar angle at the end of the interaction slidingcontact
-
- θ0:
-
- Polar angle at the beginning of the interaction slidingcontact
-
- τ:
-
- Resident time of the steel in the bubble region in the tundish
-
- ε:
-
- The inclusion removal efficiency.
Acknowledgments
The authors give thanks to the following institutions: DGEST, ITM, PROMEP, and SNI for their permanent support to the Academic Research Group on Mathematical Simulation of Materials Processing and Fluid Dynamics.




