Volume 2012, Issue 1 532870

Research Article

Open Access

Simulation and Domain Identification of Sea Ice Thermodynamic System

Corresponding Author

Bing Tan

[email protected]

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

School of Mathematics and Statistics, Nanyang Normal College, Henan, Nanyang 473061, China nynu.edu.cn

Search for more papers by this author

Peng Lu,

Peng Lu

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Zhijun Li,

Zhijun Li

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Enmin Feng,

Enmin Feng

School of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Juan Wang,

Juan Wang

School of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Bing Tan,

Corresponding Author

Bing Tan

[email protected]

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

School of Mathematics and Statistics, Nanyang Normal College, Henan, Nanyang 473061, China nynu.edu.cn

Search for more papers by this author

Peng Lu,

Peng Lu

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Zhijun Li,

Zhijun Li

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Enmin Feng,

Enmin Feng

School of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Juan Wang,

Juan Wang

School of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

First published: 12 July 2012

https://doi.org/10.1155/2012/532870

Citations: 2

Academic Editor: Armin Troesch

Share a link

Email
Wechat
Bluesky

Abstract

Based on the measured data and characteristics of sea ice temperature distribution in space and time, this study is intended to consider a parabolic partial differential equation of the thermodynamic field of sea ice (coupled by snow, ice, and sea water layers) with a time-dependent domain and its parameter identification problem. An optimal model with state constraints is presented with the thicknesses of snow and sea ice as parametric variables and the deviation between the calculated and measured sea ice temperatures as the performance criterion. The unique existence of the weak solution of the thermodynamic system is proved. The properties of the identification problem and the existence of the optimal parameter are discussed, and the one-order necessary condition is derived. Finally, based on the nonoverlapping domain decomposition method and semi-implicit difference scheme, an optimization algorithm is proposed for the numerical simulation. Results show that the simulated temperature of sea ice fit well with the measured data, and the better fit is corresponding to the deeper sea ice.

1. Introduction

Arctic sea ice cover affects the exchange of heat, energy, mass, and momentum between the atmosphere and the Arctic ocean, and it is a major component of the Arctic environment. Parkinson and Cavalieri [1] suggested that sea ice in the Arctic is a key indicator of climate change. Sea ice has been the principal threat to the development of the Arctic cruise which is cheap, reliable, and capable of year-around operation. Extremely formidable sea ice cover can restrict the operation of surface ships to a few months each summer, and even then there are areas where icebreaker assistance is still required. Meanwhile, sea ice is also a significant threat for the safe design of offshore structures and harbor facilities. Therefore, the research on sea ice has aroused interests of the scientists in many fields. Unfortunately, the physical parameters of sea ice have been obtained mainly by field measurement until now, which are spare and unsatisfactory due to the difficulties in situ, especially during the polar winter. The parameter identification method can reinforce the field data for improved understanding of the physical mechanism and variabilities of parameters of sea ice because sea ice temperature can be measured continuously and automatically. Moreover, it can help to forecast the variabilities of sea ice and climate [2–4].

Many researchers have been devoted to the establishment and improvement of the thermodynamic model of sea ice system. Maykut and Untersteinter [5] first formally proposed a comprehensive one-dimensional sea ice thermodynamic model named MU model, but the corresponding fluxes of atmosphere and ocean were not involved. Semtner [6] simplified MU model, his model has been widely used in climate simulations, while lacks universal and effectiveness. Parkinson and Washington [7] made an improvement of Semtner′s model [6], extended the thermodynamic model to a three-dimensional model on a large scale, and considered especially the impact of the leads, which are stretches of open water within fields of sea ice. Hibler [8] established a thermal-dynamic model and carried out first the numerical simulation using finite difference method. Numerical simulation and parameter identification of sea ice thermodynamic system have been paid increasing attention over the past several years, and the consideration of the thermodynamic process of sea ice has been more detailed and comprehensive [9–12]. The thickness of sea ice is one of the most important parameters in thermodynamic and dynamic models of sea ice, and it describes the vertical scale of sea ice. Unfortunately, owing to the randomness and variability of the distribution of sea ice, the continuous and accurate measurement of the thickness is very difficult. Meanwhile, the continuous changes of sea ice thickness in the numerical simulation of large-scale and long process may lead to comparatively large deviation between the simulated and measured sea ice temperatures. The introduction of the change of sea ice thickness in the thermodynamic system thus cannot only describe the thermodynamic behavior of sea ice better but also make the numerical simulation more accurately, while there is few consideration of it at present [13].

The thermodynamic process of sea ice is a heat conductivity process in nature which can be described by a parabolic partial differential equation generally. Therefore, we describe the variability of sea ice temperature in space and time by a parabolic distributed parameter system, with sea ice temperature as the state variable. A one-dimensional three-layer thermodynamic system coupled by snow, ice, and sea water is considered, and the thicknesses of snow and sea ice are identified. A distributed parameter system in a time-dependent domain is established and transferred to an abstract parabolic evolution system by some mathematical methods, and the existence and uniqueness of the weak solution of the evolution equation are proved. By taking the thicknesses of snow and sea ice as identified variables and the deviation between the calculated and measured temperature of sea ice as the performance criterion, an optimal model with state constraints is presented. Then, the existence of the optimal parameter is discussed, and the one-order necessary condition of the optimality is given. Finally, based on the nonoverlapping domain decomposition method and semi-implicit difference schemes, an optimization algorithm is constructed and applied to study the thickness and temperature of the Arctic sea ice. Through numerical simulation, we obtained the change characteristics of snow and ice thicknesses and temperature distribution in sea ice.

This paper is organized as follows. In Section 2, we present a thermodynamic system coupled by snow, ice, and sea water. Section 3 derives some important properties of a bilinear functional and proves the existence and uniqueness of the weak solution of the evolution equation. Section 4 establishes an optimal model with state constraints and proves the strong continuity of the weak solution with respect to the parameters and the existence of the optimal parameter. Moreover, the one-order necessary condition of the optimality is derived. An numerical optimization algorithm is constructed and applied to numerical simulation in Section 5, and numerical results are presented in Section 6. Some conclusions are presented in the final section.

2. The Coupled Thermodynamic System of Sea Ice

Consider the thermodynamic system of sea ice coupled by snow, ice, and sea water layers (Figure 1), denoted by snow-ice-water system. Since the gradient variation of sea ice temperature in the vertical direction is far greater than that in the horizontal direction, we only consider the heat flux in the vertical direction. Let t denote the time (unit: s), T (0 < T < ∞) the final time, and [0, T] the observation period. Set I_T : = (0, T).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Sketch of the sea ice thermodynamic model.

Let x axis be the depth direction of the snow-ice-water system (unit: m), and the point on snow surface at the initial measured time the coordinate origin (Figure 1). Let h₁(t), h₂(t), and h₃(t) be the thicknesses of snow, ice, and sea water layers at the time t ∈ I_T, respectively, then the total thickness at the time t can be expressed as

()

Obviously, the thickness of sea water at the time t can be expressed as

()

According to the physical properties of sea ice, we have h₁(t), h₂(t) ∈ C¹(I_T; R).

Let h₁(0) = h₁₀ and h₂(0) = h₂₀ be the initial thicknesses of snow and sea ice, respectively, which are known constants, then the initial thickness of sea water layer is

()

Let the initial space domains of snow, ice, and sea water layers be Ω₁₀ = (0, h₁₀], Ω₂₀ = (h₁₀, h₁₀ + h₂₀] and Ω₃₀ = (h₁₀ + h₂₀, L(0)), respectively, then the initial space domain of the system can be described as

()

obviously, Ω₀ is a nonempty, bounded, and connected set.

Additionally, let Ω₁(t) = (0, h₁(t)], Ω₂(t) = (h₁(t), h₁(t) + h₂(t)], and Ω₃(t) = (h₁(t) + h₂(t), L(t)) be the space domains of snow, ice, and sea water layers at the time t ∈ I_T, respectively, then the space domain of the snow-ice-water system at the time t ∈ I_T can be expressed as

()

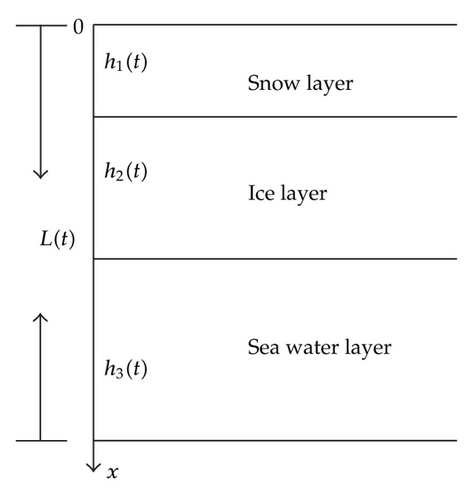
Apparently, the measured space-time domain denoted by Q_T = Ω(t) × I_T is opened and bounded.

By the energy conversation and the Fourier law, the coupled thermodynamic sea ice model is thus described by the following parabolic partial differential dynamic system

()

where ρ = ρ_i is the density, c = c_i the specific heat and K = K_i the thermal conductivity, T(x, t) the temperature of the snow-ice-water system at the depth x and the time t (unit: Kelvin), T₀(x) the temperature at the depth x and the time t = 0, and g(x, t) = g_i(x, t) the heat source term. (x, t) ∈ Ω_i × I_T, i = 1,2, 3, denotes the snow, ice, and sea water layer, respectively. Q₁(t) and T₃(t) are both known functions on the time t.

The system (2.6) is piecewise smooth owing to the difference of the densities, specific heats, and thermal conductivities in the three layers. By the physical properties of sea ice, we give the following assumptions.

(A1)
The thermodynamic parameters (ρ, c, and K) remain unchanged during the measured period.
(A2)
The upper and lower boundaries remain unmoved, namely, the total thickness of the system is a constant (L(t) = L).
(A3)
T(x, t) is continuous on .
(A4)
h₁(t), h₂(t) ∈ C²(I_T; R) are bounded functions with positive values, and there exist h_jl > 0 and h_ju > 0 satisfying h_jl ≤ h_ju, such that h_jl ≤ h_j ≤ h_ju, j = 1,2.

Additionally, functions in the system (2.6) should be differential on x or t in some sense; thus, we assume that

(A5)
, T₃(t), Q₁(t) ∈ C²(I_T; R), , i = 1,2, 3.

According to the assumptions (A1) and (A2), we set α = ρc/K, and y(x, t) = T(x, t)−(x − L)Q₁(t) − T₃(t), then the system (2.6) can be described as the following homogeneous boundary value problem denoted by (HBP):

()

where

()

3. Properties of the Coupled Thermodynamic System

For convenience, we let u₁ = h₁(t), u₂ = h₂(t), u = (u₁, u₂), and is measurable, h_jl ≤ u_j ≤ h_ju, j = 1,2} ⊂ C²(I_T; R⁺) is the admissible parameter set, Γ is a known nonempty, bounded, closed convex subset on R². And let Ω_u(t) = Ω_1u(t) ∪ Ω_2u(t) ∪ Ω_3u(t) be the spatial domain of the distributed parameter system (HBP) at the time t, where Ω_iu(t) = Ω_i(t), i = 1,2, 3.

For any

and

, let H_u(t) = L²(Ω_u(t); R) be a separable Hilbert space,

, ∂φ/∂x|_x=0 = φ|_x=L = 0} with norms denoted by

and

, respectively, then V_u(t) ⊂ H_u(t). Let

and

denote the inner product on H_u(t) and V_u(t), respectively,

and

the dual spaces of H_u(t) and V_u(t), respectively, and

the dual paring between V_u(t) and

, then

is a Gelf-triple space with

, namely, the embedding V_u(t)↪H_u(t) is continuous, and V_u(t) is dense in H_u(t). The inner product and the induced norm on H_u(t) are defined by

()

The inner product and the induced norm on V_u(t) are defined by

()

where φ_x and ψ_x are the derivatives of φ and ψ on the depth x, respectively.

The dual paring between

and V_u(t) is expressed as

()

Let ξ ∈ V_u(t), we multiply both sides of (2.7) by ξ and integrate them over Ω_u(t):

()

Using the method of integration by parts and the homogeneous boundary conditions, (3.4) can be described as

()

For any t ∈ I_T, we define a functional on V_u(t) × V_u(t) as

()

The properties of the functional a(t, u; φ, ψ) are presented in the following.

Property 1. Suppose that assumptions (A1)–(A5) hold, then

(1)
a(t, u; φ, ψ) defined by (3.6) is a bilinear functional on V_u(t) × V_u(t).
(2)
For all φ, ψ ∈ V_u(t), a(·, u; φ, ψ) is a measurable function on I_T, and there exists c > 0, such that .

Proof. (1) For all λ₁, λ₂ ∈ R, for all φ₁, φ₂, ψ₁, ψ₂ ∈ V_u(t), we have

()

So a(t, u; φ, ψ) is a bilinear functional on V_u(t) × V_u(t).

(2) Obviously, for all φ, ψ ∈ V_u(t), a(t, u; φ, ψ) is a measurable function on I_T according to (3.6), and

()

Taking c = α, then

Property 2. Suppose that assumptions (A1)–(A5) hold, then, for the bilinear functional a(t, u; φ, ψ) defined by (3.6), there exist α₀ > 0 and λ > 0, such that , for all .

Proof. The conclusion follows directly from (3.6) and Garding inequality [14].

From the Properties 1 and 2 and Lax-Milgram theorem [15], there exists a bounded continuous linear operator

, such that

()

According to (3.9), the Properties 1 and 2, we can get the following property.

Property 3. Suppose that assumptions (A1)–(A5) hold, then for all , for all φ, ψ ∈ V_u(t), and for all , there exist M₁ > 0 and M₂ > 0, such that

()

For any , φ ∈ V_u(t), and , set , then H(t, u; φ) is a continuous linear functional on V_u(t). According to Riesz representation theorem [14], there exists a unique element , such that

()

From the above, for each , the system (HBP) can be written as a parabolic evolution equation denoted by (PEE):

()

where

, and

with the inner product defined as

()

Obviously, the above process is reversible, the system (PEE) is thus equivalent to (HBP). The definition of weak solution of the system (PEE) is given in the following.

Definition 3.1. A function is a weak solution of (PEE), if y(t, x; u) satisfies

()

where ξ ∈ V_u(t) and

Theorem 3.2. Suppose that assumptions (A1)–(A5), Properties 1 and 3 hold. For all , let Ω_u(t) = x_u(t, Ω₀) is bounded, and there exists a countable base {φ₁(t), φ₂(t), …} on V_u(t), such that , i = 1,2, … . Then, the system (PEE) has a unique weak solution which depends continuously on f and y₀.

Proof. Let , here n(x) is the outward normal vector of ∂Ω_u(t) at x. By the definition of V_u(t), we know that ψ ∈ V_u(t) satisfies the Dirichlet condition (ψ(x) = 0, ) for any given . The system (PEE) thus has a unique weak solution which depends continuously on f and y₀ [15].

From the above theorem, we can also know that the system (HBP) has a unique solution .

4. Parameter Identification of the Coupled System

4.1. Identification Model

We define the performance criterion as

()

with

()

where T(t, x; u) is the temperature function obtained from the system (2.6),

is the observed temperature. Let

, then (4.1) is expressed as

()

The goal of this study is to make the temperature T(t, x; u) obtained from the system (2.6) fits the measured data as far as possible. Then, the identification model of the system (HBP) is expressed as

where

is the solution of system (HBP) corresponding to

, and J(u) is defined by (4.1).

Obviously, from (4.1)–(4.2), we can conclude that the problem (SIP) is equivalent to the following problem

where

is the solution of system (2.6) corresponding to

4.2. Strong Continuity of the Weak Solution on Parameters

Theorem 4.1. Suppose that assumptions (A1)–(A5) hold, then the mapping u → y(t, x; u) is strongly continuous.

Proof. For any given parameter , let be a feasible parameter sequence, such that ∥u_n − u₀∥→0 as n → ∞, and y_n and y₀ the solutions of (PEE) corresponding to u_n and u₀, respectively. Set w_n = y_n − y₀, p_n = p(t, x; u_n), p₀ = p(t, x; u₀), then we obtain the following system

()

Multiply both sides of the first equation of (4.4) by w_n and integrate them over Ω_u(t)×[0, t], then we have

()

For the first term of (4.5) on the left side, we have

()

For the second term of (4.5) on the left side, according to Property 2, we have

()

where α₀ and λ are the same with that of Property 2.

Using the elementary inequality ab ≤ (1/2ɛ)a² + (ɛ/2)b² and taking ɛ = α₀, then, for the right terms of (4.5), we have

()

Let . Substituting (4.6)–(4.8) into (4.5), then we have

()

Using Gronwall inequality, we obtain

()

From all the above and ∥u_n − u₀∥→0, we get |p_n − p₀ | → 0, the mapping u → y(t, x; u) is thus strongly continuous.

4.3. Existence of Optimal Parameter

Theorem 4.2. Suppose that assumptions (A1)–(A5) hold, then there exists at least one optimal parameter satisfies the identification problem (SIP).

Proof. Obviously, f₀(u) is continuous on V_u(t), and, from (4.3), dx dt ≥ 0. By Theorem 4.1, the mapping u → y(t, x; u) is continuous. Hence, the mapping u → J(u) is continuous on . Since is a nonempty, bounded, and closed set, there exists , such that for all , J(u^*) ≤ J(u), e.g., is an optimal parameter, thus the desired result is obtained.

4.4. Necessary Optimality Condition

Let be the optimal parameter of the problem (SIP), following the convex compactness of and the continuity of J(u) on , we can prove that J(u(·)) is Gateaux differentiable at and its Gateaux derivative DJ(u^*(·)) exists. Hence, we can get the following necessary conditions for optimality.

Theorem 4.3. Suppose that assumptions (A1)–(A5) are valid, and let be the optimal parameter of the system (SIP), then u^*(·) satisfies the following inequality:

()

5. Optimization and Numerical Algorithm

5.1. Optimization of the Parameter Identification Model

In this section, we aim at constructing an optimal algorithm to solve the parameter identification problem (SIPO). On the domain Ω_i(t), we decompose (2.6) as

()

with the initial condition

()

and the boundary and penetrating conditions

()

Denote the subsystem composed by (5.1), (5.2), and (5.3) as (IBP) ₁, by (5.1), (5.2), and (5.4) as (IBP) ₂, and (5.1), (5.2), and (5.5) as (IBP) ₃.

According to the partial differential theory, we can obtain the following theorem.

Theorem 5.1. Suppose that assumptions (A1)–(A5) are valid, then, for any , the subsystem (IBP) _i has a unique weak solution T_i(x, t; u) ∈ C(Ω_i(t), I_T, U_ad; R) which depends continuously on .

Let M, N be the numbers of the measured spatial and temporal spots, respectively, x_k the measured depth, t_j the measured time, T(x_k, t_j; u) the calculated temperature of sea ice at depth x_k and time t_j from the system (2.6),

the measured temperature data at depth x_k and time t_j, then the practical identification problem can be expressed as

Let

is the solution of the subsystem (IBP) _i corresponding to

, and for the numerical implementation, the problem (SIPOD) can be decomposed to the following three connected subproblems

Obviously, the performance function of (SIPOD) can be described as

()

From Theorem 4.2, we can get that there also exists at least one optimal parameter satisfying the subproblem (SIPODi).

Set

()

then, the identification problem is expressed as

and the subidentification problem is

Theorem 5.2. If u^* is the optimal parameter of SIPOD, then u^* is also that of (SIPODb).

5.2. Numerical Optimization Algorithm

In this section, the semi-implicit finite difference scheme [15] is employed to discretize, and the nonoverlapping Schwarz alternating direction method to solve (5.1). And related to the measured temperature data {T(z_k, t_j)}, a numerical optimization algorithm is constructed with the following steps.

Step 1. Select starting points , n directions e₁, e₂, …, e_n, starting step length Δu = (Δu₁, Δu₂), Δu₁ > 0, Δu₂ > 0, acceleration factor α, accuracy ɛ > 0, and the maximum iteration number k_max, set v⁰ = u⁰, k = j = 0;

Step 2. Calculate the numerical solution T(x, t; v^j), by nonoverlapping Schwarz alternating direction method and semi-implicit difference scheme.

Step 3. If J_b(v^j + Δu · e_j) < J_b(v^j), set v^j+1 = v^j + Δu · e_j; for the case J_b(v^j + Δu · e_j) ≥ J_b(v^j), if J_b(v^j − Δu · e_j) < J_b(v^j), set v^j+1 = v^j − Δu · e_j, else, set v^j+1 = v^j.

Step 4. If j < n, set j = j + 1, go to Step 3; for the case j = n, if J_b(vⁿ⁺¹) ≤ J_b(u^k), go to Step 5, else, go to Step 6.

Step 5. Set u^k+1 = vⁿ⁺¹, v⁰ = u^k+1 + α(u^k+1 − u^k), k = k + 1, and j = 0, go to Step 2.

Step 6. If k ≥ k_max, stop, set u^* = u^k, else, set v⁰ = u^k, u^k+1 = u^k, k = k + 1, and j = 0, go to Step 2.

6. Numerical Results

Using the above optimal algorithm, we can obtain the temperature distribution T(x_k, t_j; u) of sea ice in the Arctic. The data set was measured by a monitor buoy installed on floe ice in the Arctic.

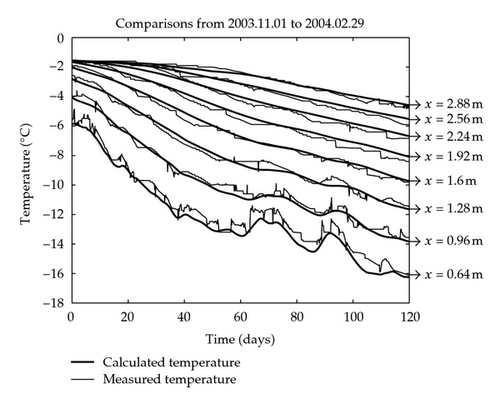
The comparison between the calculated and measured sea ice temperatures from November 1, 2003 to February 29, 2004 was shown in Figure 2, with the test temperatures data being smoothed for the unomitted transparent errors in some of the original data. The measured and simulated data in Figure 2 both indicate a general increasing trend of the temperature of sea ice, while a decreasing increment with increasing depth of sea ice. Meanwhile, because the data had been measured during the freezing period of sea ice, the temperature generally decreases with increasing time. The calculated temperature fits well with the measured data; furthermore, the better fit between the calculated and measured temperatures is corresponding to the deeper sea ice. The temperature deviation between the simulated and measured temperatures is 0.361, which is a much small error for the temperature of sea ice. It can be concluded that the numerical results by our method reflect the actual variation of the sea ice temperature distribution and approach the measured data well.

7. Conclusions

In this study, we aim to simulate the temperature of sea ice with thicknesses of snow and sea ice as identified parameters. We established a parabolic distributed system of the temperature field of sea ice with a time-dependent domain in the Arctic sea ice and proposed its parameter identification problem with thicknesses of snow and sea ice as identified variables and the deviation between the calculated and measured sea ice temperatures as the performance criterion. And we proved the unique existence of the weak solution of the thermodynamic system, discussed the existence of the optimal parameter, and derived the one-order necessary condition. Finally, based on the nonoverlapping domain decomposition method and semi-implicit difference scheme, we constructed an optimization algorithm to simulate the sea ice temperature in the Arctic. The results (Figure 2) show that the temperature of sea ice increases with increasing depth of sea ice, while, because the measurement had been made during the freezing period of sea ice, it decreases with increasing time.

The simulated temperatures of sea ice fitted well with the measured data, and the deviation between the simulated and measured temperature of sea ice was slight. It indicates that the numerical results by our method reflect the actual variation of the sea ice temperature distribution in space and time. Meanwhile, it is illuminated that the algorithm proposed in the present study is valid and more suitable for the deeper sea ice.

Nevertheless, it is important to note that our mathematical framework was verified only using in situ data from the Arctic, and the variabilities of the physical parameters of the coupled sea ice system, such as density, specific heat, were not considered, more measurements would be required for a true verification of this method in the future work. However, we believe that our method is a promising approach worthy of further studies under different environmental conditions in the Arctic as well as in the Antarctic.

Acknowledgments

The authors are grateful to Chinese Arctic and Antarctic Administration for the logistic support during the field investigation in the Arctic Ocean. This study was supported by the National Nature Science Foundation of China (Grants no. 40930848, 50921001, and 10871033), and Norwegian Research Council Project AMORA (no. 193592/S30).

References

1 Parkinson C. L. and Cavalieri D. J., Arctic sea ice variability and trends, 1979–2006, Journal of Geophysical Research C. (2008) 113, no. 7, 2-s2.0-51749103540, https://doi.org/10.1029/2007JC004558, C07003.
10.1029/2007JC004558
Web of Science® Google Scholar
2 Drobot S. D., Using remote sensing data to develop seasonal outlooks for Arctic regional sea-ice minimum extent, Remote Sensing of Environment. (2007) 111, no. 2-3, 136–147, 2-s2.0-35448974887.
10.1016/j.rse.2007.03.024
Web of Science® Google Scholar
3 Budikova D., Role of Arctic sea ice in global atmospheric circulation: a review, Global and Planetary Change. (2009) 68, no. 3, 149–163, 2-s2.0-67949117126, https://doi.org/10.1016/j.gloplacha.2009.04.001.
10.1016/j.gloplacha.2009.04.001
Web of Science® Google Scholar
4 Pritchard R. S., Li G., and Davis R. O., A deterministic-statistical sea ice drift forecast model, Cold Regions Science and Technology. (2012) 76-77, 52–62.
10.1016/j.coldregions.2011.08.003
Web of Science® Google Scholar
5 Maykut G. A. and Untersteiner N., Some results from a time dependent thermodynamic model of sea ice, Journal of Geophysical Oceanography. (1971) 76, no. 6, 1550–1575, 2-s2.0-0015019401.
10.1029/JC076i006p01550
Google Scholar
6 Semtner A. J., A model for the thermodynamic growth of sea ice in numerical investigation of climate, Journal of Physical Oceanography. (1976) 6, 379–389.
10.1175/1520-0485(1976)006<0379:AMFTTG>2.0.CO;2
Web of Science® Google Scholar
7 Parkinson C. L. and Washington W. M., A large-scale numerical model of sea ice, Journal of Geophysical Oceanography. (1979) 84, no. C1, 311–337.
10.1029/JC084iC01p00311
Web of Science® Google Scholar
8 Hibler W. D., A dynamic thermodynamic sea ice model, Journal of Geophysical Oceanography. (1979) 9, 817–846.
10.1175/1520-0485(1979)009<0815:ADTSIM>2.0.CO;2
Web of Science® Google Scholar
9 Ikehata M., An inverse source problem for the heat equation and the enclosure method, Inverse Problems. (2007) 23, no. 1, 183–202, 2-s2.0-33947661404, https://doi.org/10.1088/0266%2D5611/23/1/009.
10.1088/0266-5611/23/1/009
Web of Science® Google Scholar
10 Rincon M. A., Lmaco J., and Liu I. S., A nonlinear heat equation with temperature-dependent parameters, Mathematical Physics Electronic Journal. (2006) 12, 1–21, 2-s2.0-33750977558.
Google Scholar
11 Shidfar A. and Karamali G. R., Numerical solution of inverse heat conduction problem with nonstationary measurements, Applied Mathematics and Computation. (2005) 168, no. 1, 540–548, 2-s2.0-25644451088, https://doi.org/10.1016/j.amc.2004.09.028.
10.1016/j.amc.2004.09.028
Web of Science® Google Scholar
12 Reid T. and Crout N., A thermodynamic model of freshwater Antarctic lake ice, Ecological Modelling. (2008) 210, no. 3, 231–241, 2-s2.0-36148976428, https://doi.org/10.1016/j.ecolmodel.2007.07.029.
10.1016/j.ecolmodel.2007.07.029
Web of Science® Google Scholar
13 Fang H., Wang J., Feng E., and Li Z., Parameter identification and application of a distributed parameter coupled system with a movable inner boundary, Computers and Mathematics with Application. (2011) 62, no. 11, 4015–4020, https://doi.org/10.1016/j.camwa.2011.09.035, 2859957.
10.1016/j.camwa.2011.09.035
Web of Science® Google Scholar
14 Zhang G. Q. and Lin Y. Q., Functional Analysis, 2003, Beijing University Press, Beijing, China, (in Chinese).
Google Scholar
15 Wang Y. D., L2 Theories on Partial Differential Equation, 1989, Beijing University Press, Beijing, China, (in Chinese).
Google Scholar

Citing Literature

All articles

Simulation and Domain Identification of Sea Ice Thermodynamic System

Abstract

1. Introduction

2. The Coupled Thermodynamic System of Sea Ice

3. Properties of the Coupled Thermodynamic System