Journal of Applied Mathematics
Volume 2012, Issue 1 523812
Research Article
Open Access

LMI Approach to Stability Analysis of Cohen-Grossberg Neural Networks with p-Laplace Diffusion

Xiongrui Wang, 

Xiongrui Wang

Department of Mathematics, Yibin University, Yibin 644007, China yibinu.cn

Institute of Mathematics, Yibin University, Yibin 644007, China yibinu.cn

Search for more papers by this author
Ruofeng Rao, 

Corresponding Author

Ruofeng Rao

Department of Mathematics, Yibin University, Yibin 644007, China yibinu.cn

Institute of Mathematics, Yibin University, Yibin 644007, China yibinu.cn

Search for more papers by this author
Shouming Zhong, 

Shouming Zhong

Institute of Mathematics, Yibin University, Yibin 644007, China yibinu.cn

College of Applied Mathematics, University of Electronic Science and Technology of China, Chengdu 610054, China uestc.edu.cn

Search for more papers by this author
First published: 24 December 2012
https://doi.org/10.1155/2012/523812
Citations: 4
Academic Editor: Zhilong L. Huang

Abstract

The nonlinear p-Laplace diffusion (p > 1) was considered in the Cohen-Grossberg neural network (CGNN), and a new linear matrix inequalities (LMI) criterion is obtained, which ensures the equilibrium of CGNN is stochastically exponentially stable. Note that, if p = 2, p-Laplace diffusion is just the conventional Laplace diffusion in many previous literatures. And it is worth mentioning that even if p = 2, the new criterion improves some recent ones due to computational efficiency. In addition, the resulting criterion has advantages over some previous ones in that both the impulsive assumption and diffusion simulation are more natural than those of some recent literatures.

1. Introduction and Preparation

It is well known that Cohen-Grossbeg neural network (CGNN) was proposed by Cohen and Grossberg [1] in 1983. Since then there have been a lot of interested results obtained in many literatures (see [2–9]) due to its general applications, such as pattern recognition, image and signal processing, optimization automatic control, and artificial intelligence. Usually, there exist the impulsive effect and time-varying delays phenomenon in various neural networks [3, 5–7, 10–14]. Besides, diffusion effects cannot be avoided in the neural networks when electrons are moving in asymmetric electromagnetic fields [15–18]. However, diffusion disturbance was always simulated simply by linear Laplace diffusion [15–18]. Few papers involved the nonlinear reaction-diffusion [19]. So in this paper, we investigate the stability of the following stochastic CGNN with nonlinear p-Laplace diffusion (p > 1):
()
where Ω is a bounded subset in Rm with smooth boundary ∂Ω, and ∂ui(t, x)/∂ν = ((∂ui(t, x)/∂x1), (∂ui(t, x)/∂x2), …, (∂ui(t, x)/∂xm)) T denotes the outward normal derivative on ∂Ω.

Remark 1.1. If p = 2, system (1.1) was studied by [5] though there is a little difference between Dirichlet boundary condition and Neumann boundary condition. However, our impulsive assumption is more natural than that of [5], which will result in some difference in methods.

Here, M is a diagonal matrix, Ω ∈ Rm is a bounded compact set with smooth boundary, u = (u1, u2, …, un) T ∈ Rn, and w(t) = (w1(t), w2(t), …, wn(t)) T is a n-dimensional Brownian motion defined on a complete probability space (Ω, ℱ, P) with the natural filtration {ℱt} t≥0 generated by the process {w(s) : 0 ≤ s ≤ t}. We associate Ω with the canonical space generated by all {wi(t)} and denoted by ℱ the associated σ-algebra generated by w(t) with the probability measure p. A(u(t, x)) presents an amplification function, B(u(t, x)) is an appropriately behavior function, and f and g denote the activation function. τ(t)  (0 ≤ τ(t) ≤ τ) corresponds to the transmission delays at time, and tk is called the impulsive moment with 0 < t1 < t2 < ⋯<tk < ⋯ and lim k→∞tk = +∞. We always assume . ∇pu = (∇pu1, …, ∇pun) T, ∇pui = (|∇ui|p−2(∂ui/∂x1), …, |∇ui|p−2(∂ui/∂xm)) T,  is Hadamard product of matrix and ∇pu [20]. Here, the diffusion parameters matrix is denoted simply as . Let Yi = (yi1, …, yim) T,  i = 1,2, …, n, and matrix 𝕐 = (Y1, …, Yn) T, and we denote . Particularly, ∇pu = ∇u for the case of p = 2.

Remark 1.2. Diffusion effects always occur in the neural networks when electrons are moving in asymmetric electromagnetic fields [15–18], and diffusion behavior is so complicated that it cannot always be simulated by linear Laplace diffusion. So in this paper, the nonlinear p-Laplace diffusion is considered in System (1.1).

Assume, in addition, the following.
  • (H1)

    A(u(t, x)) is a bounded, positive, and continuous diagonal matrix, that is, there exist two positive diagonal matrices and such that .

  • (H2)

    such that there exists a positive diagonal matrix B = diag (B1, B2, …, Bn) satisfying (bi(ui(t, x))/ui(t, x)) ≥ Bi for all i.

  • (H3)

    There exist two positive diagonal matrices F = diag (F1, F2, …, Fn) and G = diag (G1, G2, …, Gn) such that

    ()

  • (H4)

    The null solution is the equilibrium point of system (1.1), that is, the following conditions hold:

    ()

where the symmetrical matrix Q > 0.
For convenience′s sake, we introduce some standard notations
  • (i)

    L2(R)(R × Ω): the space of real Lebesgue measurable functions of R × Ω, it is a Banach space for the 2-norm with ∥ui(t)∥ = (∫Ω  | ui(t, x)|2dx) 1/2, where |ui(t, x)| is Euclid norm.

  • (ii)

    : the family of all F0-measurable C([−τ, 0] × Ω; Rn-) value random variable ξ = {ξ(θ, x):−τ ≤ θ ≤ 0,  x ∈ Ω} such that , where E{·} stands for the mathematical expectation operator with respect to the given probability measure p.

  • (iii)

    Q = (qij) n×n > 0 (<0): a positive (negative) definite symmetrical matrix, that is, yTQy > 0 (<0) for any 0 ≠ y ∈ Rn.

  • (iv)

    Q = (qij) n×n ≥ 0 (≤0): a semipositive (semi-negative) definite symmetrical matrix, that is, yTQy ≥ 0 (≤0) for any y ∈ Rn.

  • (v)

    : this means is a semi-positive (semi-negative) symmetrical definite matrix.

  • (vi)

    : this means is a positive (negative) symmetrical definite matrix.

  • (vii)

    λmax (Φ),  λmin (Φ) denotes the largest and smallest eigenvalue of symmetrical matrix Φ, respectively.

  • (viii)

    I: identity matrix with compatible dimension.

  • (ix)

    Denote |C | = (|cij | ) n×n for any matrix Cn×n; |u(t, x)| = (|u1 | , |u2 | , …, |un|) for any u ∈ Rn.

Let u(t, x; φ) denote the state trajectory from the initial data u(t0 + θ, x; φ) = φ(θ, x) on −τ ≤ θ ≤ 0 in .

Definition 1.3. The null solution of impulsive system (2.2) is globally stochastically exponentially stable in the mean square if for every , there exists scalars β > 0 and γ > 0 such that

()

Lemma 1.4 (see [11].)Let U, P be any matrices, ε > 0 is a positive number and matrix H = HT > 0, then

()

Lemma 1.5 (Schur complement [3]). The LMI

()
where matrix S(t) and symmetrical matrices Q(t) and  R(t) depend on t, is equivalent to any one of the following conditions:
  • (L1)

    R(t) > 0,   Q(t) − S(t)R−1(t)ST(t) > 0;

  • (L2)

    Q(t) > 0,   R(t) − ST(t)Q−1(t)ST(t) > 0.

Lemma 1.6 (see [21].)Consider the following differential inequality:

()
where and v(t) is continuous except tk, k = 1, 2, …, where it has jump discontinuities. The sequence tk satisfies 0 = t0 < t1 < t2 < ⋯<tk < tk+1 < ⋯, and lim k→∞tk = ∞. Suppose that
  • (1)

    a > b ≥ 0;

  • (2)

    tk − tk−1 > δτ, where δ > 1, and there exist constants γ > 0,  M > 0 such that

    ()

where ρi = max {1, ai + bieλτ}, λ > 0 is the unique solution of equation λ = a − beλτ then
()
In addition, if θ = sup k∈Z{1, ak + bkeλτ}, then
()

Computer simulation is shown in Figures 1, 2, 3, and 4.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Computer simulation of the state  u1(t, x).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Sectional curve of the state variable u1(t, x).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Computer simulation of the state u2(t, x).
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Sectional curve of the state variable u2(t, x).

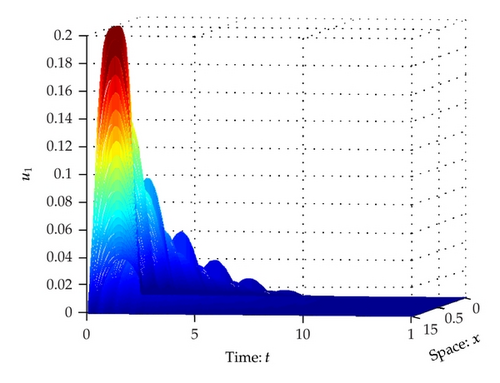
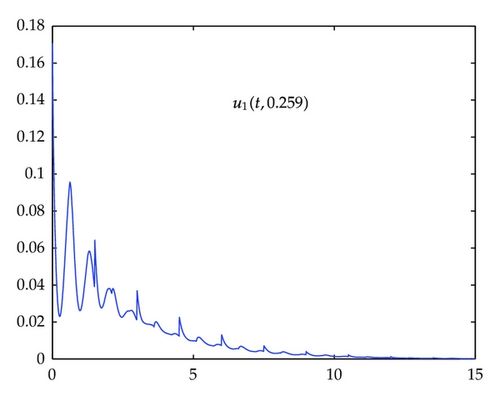
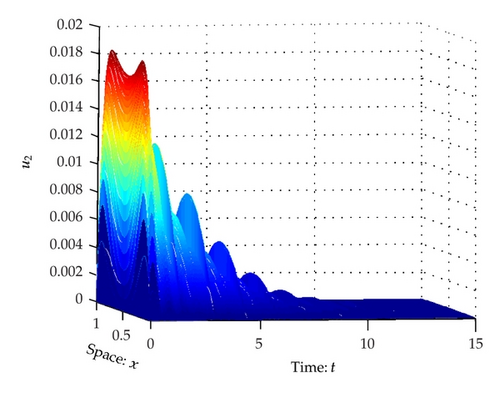
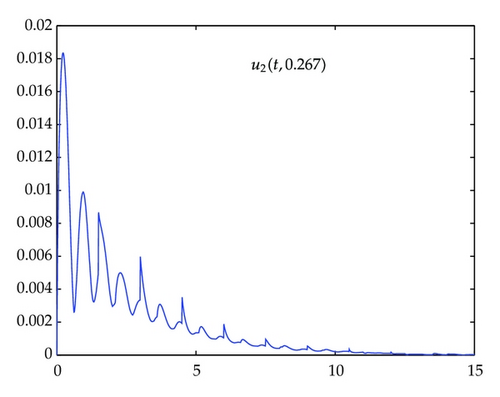
2. Main Results

Theorem 2.1. If assumptions (H1)–(H4) hold, in addition, the following conditions are satisfied:

  • (C1)

    there exists diagonal matrices P1 = diag (p11, p12, …, p1n) > 0 and P2 > 0 such that

    ()

  • (C2)

    min {(λmin Θ/λmax P1), (1 − μ)}>(λmax G2/λmin P2) ≥ 0, where , where τ′(t) ≤ μ < 1 for all t;

  • (C3)

    there exists a constant δ > 1 such that inf k∈Z(tk − tk−1) > δτ, δ2τ > ln (ρeλτ) and λ − (ln (ρeλτ)/δτ) > 0, where λ > 0 is the unique solution of the equation λ = a − beλτ, and ρ = max {1, (λmax (MP1M)/λmin P1) + eλτ}, a = min {(λmin Θ/λmax P1), (1 − μ)}, b = λmax G2/λmin P2, then the null solution of system (1.1) is stochastically exponentially stable with convergence rate (1/2)(λ − (ln (ρeλτ)/δτ)).

Proof. First, we can get by Guass formula (see [20, Lemma 2.3])

()

Construct the Lyapunov functional as follows:

()
where
()

Then

()
And then we have
()

Next, we use the method similar as that of [22]. Since u(t, x) is the solution of system, and V(u(t, x)) ∈ C2[Rm, R+] for all t, we can get by formula

()

Then we have

()

Thus, for small enough Δt > 0, we have

()
and then
()
Since
()

Then,

()
Next, we have
()

Now the conditions (C1)–(C3) and Lemma 1.6 deduce

()
or
()
which together with Definition 1.3 implies the accomplishment of the proof.

Remark 2.2. The nonlinear p-Laplace diffusion (p > 1) brings a great difficulties in judging the stability. However, even if p = 2, Theorem 2.1 has more computational efficiency than [15, Theorem 3.1] due to LMI criterion.

3. Examples

Consider the following impulsive CGNN:
()
where , and the corresponding matrices
()
We might as well assume that t0 = 0,  tk − tk−1 = 0.525,  τ(t) = 0.65,  τ′(t) ≤ μ = 0.99 for all t ≥ t0, and
()
By way of MATLAB LMI Control Toolbox, we can solve the LMI condition in (C1) and get
()
Next, we will prove that such P1 and P2 make (C2) and (C3) hold. Indeed, by computing directly, we can obtain a = 0.01,  b = 0.0081, and then (C2) holds. Moreover, we might as well assume δ = 82, and then we have λ = 0.0019,  ρ = 2.8235, thus (C3) is satisfied. Now from Theorem 2.1 we can compute the convergence 9.3809*10−0.004.

4. Conclusions

In this paper, we investigate the influence of impulse, time-delays and diffusion behaviors on the stability of stochastic Cohen-Grossberg neural network (CGNN). The LMI conditions of stochastic exponential stability of impulsive CGNN with p-Laplace reaction-diffusion terms was given, and an illustrate example was also given to show the effectiveness of the obtained result. Besides, the result obtained in this paper is also valid to the Laplace reaction-diffusion (in the case of p = 2) and has more computational efficiency due to the LMI approach even if p = 2 (Remark 2.2).

Acknowledgments

This work was supported by the National Basic Research Program of China (2010CB732501), by Scientific Research Fund of Science Technology Department of Sichuan Province 2011JYZ010, and by Scientific Research Fund of Sichuan Provincial Education Department (11ZA172, 12ZB349).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.