Journal of Applied Mathematics
Volume 2012, Issue 1 514504
Research Article
Open Access

Robust Adaptive Switching Control for Markovian Jump Nonlinear Systems via Backstepping Technique

Jin Zhu, 

Corresponding Author

Jin Zhu

Department of Automation, University of Science and Technology of China, Hefei, Anhui 230027, China ustc.edu.cn

Search for more papers by this author
Hongsheng Xi, 

Hongsheng Xi

Department of Automation, University of Science and Technology of China, Hefei, Anhui 230027, China ustc.edu.cn

Search for more papers by this author
Qiang Ling, 

Qiang Ling

Department of Automation, University of Science and Technology of China, Hefei, Anhui 230027, China ustc.edu.cn

Search for more papers by this author
Wanqing Xie, 

Wanqing Xie

Center of Information Science Experiment and Education, University of Science and Technology of China, China ustc.edu.cn

Search for more papers by this author
First published: 18 July 2012
https://doi.org/10.1155/2012/514504
Citations: 3
Academic Editor: Xianxia Zhang

Abstract

This paper investigates robust adaptive switching controller design for Markovian jump nonlinear systems with unmodeled dynamics and Wiener noise. The concerned system is of strict-feedback form, and the statistics information of noise is unknown due to practical limitation. With the ordinary input-to-state stability (ISS) extended to jump case, stochastic Lyapunov stability criterion is proposed. By using backstepping technique and stochastic small-gain theorem, a switching controller is designed such that stochastic stability is ensured. Also system states will converge to an attractive region whose radius can be made as small as possible with appropriate control parameters chosen. A simulation example illustrates the validity of this method.

1. Introduction

The establishment of modern control theory is contributed by state space analysis method which was introduced by Kalman in 1960s. This method, describing the changes of internal system states accurately through setting up the relationship of internal system variables and external system variables in time domain, has become the most important tool in system analysis. However, there remain many complex systems whose states are driven by not only continuous time but also a series of discrete events. Such systems are named hybrid systems whose dynamics vary with abrupt event occurring. Further, if the occurring of these events is governed by a Markov chain, the hybrid systems are called Markovian jump systems. As one branch of modern control theory, the study of Markovian jump systems has aroused lots of attention with fruitful results achieved for linear case, for example, stability analysis [1, 2], filtering [3, 4] and controller design [5, 6], and so forth. But studies are far from complete because researchers are facing big challenges while dealing with the nonlinear case of such complicated systems.

The difficulties may result from several aspects for the study of Markovian jump nonlinear systems (MJNSs). First of all, controller design largely relies on the specific model of systems, and it is almost impossible to find out one general controller which can stabilize all nonlinear systems despite of their forms. Secondly Markovian jump systems are applied to model systems suffering sudden changes of working environment or system dynamics. For this reason, practical jump systems are usually accompanied by uncertainties, and it is hard to describe these uncertainties with precise mathematical model. Finally, noise disturbance is an important factor to be considered. More often that not, the statistics information of noise is unknown when taking into account the complexity of working environment. Among the achievements of MJNSs, the format of nonlinear systems should be firstly taken into account. As one specific model, the nonlinear system of strict-feedback form is well studied due to its powerful modelling ability of many practical systems, for example, power converter [7], satellite attitude [8], and electrohydraulic servosystem [9]. However, such models should be modified since stochastic structure variations exist in these practical systems, and this specific nonlinear system has been extended to jump case. For Markovian jump nonlinear systems of strict-feedback form, [10, 11] investigated stabilization and tracking problems for such MJNSs, respectively. And [12] studied the robust controller design for such systems with unmodeled dynamics. However, for the MJNSs suffering aforementioned factors in this paragraph, research work has not been performed yet.

Motivated by this, this paper focuses on robust adaptive controller design for a class of MJNSs with uncertainties and Wiener noise. Compared with the existing result in [12], several practical limitations are considered which include the following: the uncertainties are with unmodeled dynamics, and the upper bound of dynamics is not necessarily known. Meanwhile the statistics information of Wiener noise is unknown. Also the adaptive parameter is introduced to the controller design whose advantage has been described in [13]. The control strategy consists of several steps: firstly, by applying generalized formula, the stochastic differential equation for MJNS is deduced and the concept of JISpS (jump input-to-state practical stability) is defined. Then with backstepping technology and small-gain theorem, robust adaptive switching controller is designed for such strict-feedback system. Also the upper bound of the uncertainties can be estimated. Finally according to the stochastic Lyapunov criteria, it is shown that all signals of the closed-loop system are globally uniformly bounded in probability. Moreover, system states can converge to an attractive region whose radius can be made as small as possible with appropriate control parameters chosen.

The rest of this paper is organized as follows. Section 2 begins with some mathematical notions including differential equation for MJNS, and we introduce the notion of JISpS and stochastic Lyapunov stability criterion. Section 3 presents the problem description, and a robust adaptive switching controller is given based on backstepping technique and stochastic small-gain theorem. In Section 4, stochastic Lyapunov criteria are applied for the stability analysis. Numerical examples are given to illustrate the validity of this design in Section 5. Finally, a brief conclusion is drawn in Section 6.

2. Mathematical Notions

2.1. Stochastic Differential Equation of MJNS

Throughout the paper, unless otherwise specified, we denote by a complete probability space with a filtration satisfying the usual conditions (i.e., it is right continuous and ℱ0 contains all p-null sets). Let |x| stand for the usual Euclidean norm for a vector x, and let ∥xt∥ stand for the supremum of vector x over time period [t0, t], that is, . The superscript T will denote transpose and we refer to Tr (·) as the trace for matrix. In addition, we use L2(P) to denote the space of Lebesgue square integrable vector.

Take into account the following Markovian jump nonlinear system:
()
where x ∈ ℝn, u ∈ ℝm are state vector and input vector of the system, respectively. r(t), t ≥ 0 is named system regime, a right-continuous Markov chain on the probability space taking values in finite state space S = {1,2, …, N}. And ω(t) = {ω1, ω2, …, ωl} is l-dimensional independent Wiener process defined on the probability space, with covariance matrix E{dωdωT} = Υ(t)ΥT(t)dt, where Υ(t) is an unknown bounded matrix-value function. Furthermore, we assume that the Wiener noise ω(t) is independent of the Markov chain r(t). The functions f : ℝn+m × ℝ+ × S → ℝn and g : ℝn+m × ℝ+ × S → ℝn×l are locally Lipschitz in (x, u, r(t) = k) ∈ ℝn+m × S for all t ≥ 0; namely, for any h > 0, there is a constant Kh ≥ 0 such that
()
()
It is known by [2] that with (2.3) standing, MJNS (2.1) has a unique solution.
Considering the right-continuous Markov chain r(t) with regime transition rate matrix , the entries πkj, k, j = 1,2, …, N are interpreted as transition rates such that
()
where dt > 0 and o(dt) satisfies lim dt→0 (o(dt)/dt) = 0. Here πkj > 0(k ≠ j) is the transition rate from regime k to regime j. Notice that the total probability axiom imposes πkk negative and
()
For each regime transition rate matrix Π, there exists a unique stationary distribution ζ = (ζ1, ζ2, …, ζN) such that [14]
()
Let C2,1(ℝn × ℝ+ × S) denote the family of all functions F(x, t, k) on ℝn × ℝ+ × S which are continuously twice differentiable in x and once in t. Furthermore, we give the stochastic differentiable equation of F(x, t, k) as
()
where M(t) = (M1(t), M2(t), …, MN(t)) is a martingale process.
Take the expectation in (2.7), so that the the infinitesimal generator produces [2, 15]
()

Remark 2.1. Equation (2.7) is the differential equation of MJNS (2.1). It is given by [12], and the similar result is also achieved in [15]. Compared with the differential equation of general nonjump systems, two parts come forth as differences: transition rates πkj and martingale process M(t), which are both caused by the Markov chain r(t). And we will show in the following section that the martingale process also has effects on the controller design.

2.2. JISpS and Stochastic Small-Gain Theorem

Definition 2.2. MJNS (2.1) is JISpS in probability if for any given ϵ > 0, there exist 𝒦ℒ function β(·, ·), 𝒦∞ function γ(·), and a constant dc ≥ 0 such that

()

Remark 2.3. The definition of ISpS (input-to-state practically stable) in probability for nonjump stochastic system is put forward by Wu et al. [16], and the difference between JISpS in probability and ISpS in probability lies in the expressions of system state x(t, k) and control signal ut(k). For nonjump system, system state and control signal contain only continuous time t with k ≡ 1. While jump systems concern with both continuous time t and discrete regime k. For different regime k, control signal ut(k) will differ with different sample taken even at the same time t, and that is the reason why the controller is called a switching one. Based on this, the corresponding stability is called Jump ISpS, and it is an extension of ISpS. Let k ≡ 1, and the definition of JISpS will degenerate to ISpS.

Consider the jump interconnected dynamic system described in Figure 1:
()
where is the state of system, Ξi(r(t)),   i = 1,2 denotes exterior disturbance and/or interior uncertainty. Wti is independent Wiener noise with appropriate dimension, and we introduce the following stochastic nonlinear small-gain theorem as a lemma, which is an extension of the corresponding result in Wu et al. [16].
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Interconnected feedback system.

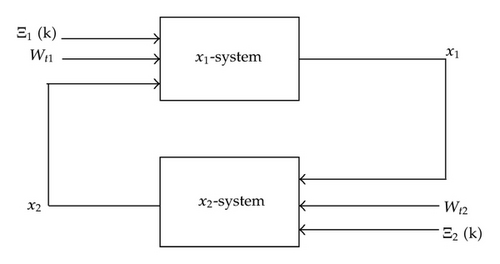
Lemma 2.4 (stochastic small-gain theorem). Suppose that both the x1-system and x2-system are JISpS in probability with (Ξ1(k), x2(t, k)) as input and x1(t, k) as state and (Ξ2(k), x1(t, k)) as input and x2(t, k) as state, respectively; that is, for any given ϵ1, ϵ2 > 0,

()
hold with βi(·, ·) being 𝒦ℒ function, γi and γwi being 𝒦∞ functions, and di being nonnegative constants, i = 1,2.

If there exist nonnegative parameters ρ1, ρ2, s0 such that nonlinear gain functions γ1, γ2 satisfy

()
the interconnected system is JISpS in probability with Ξ(k) = (Ξ1(k), Ξ2(k)) as input and x = (x1, x2) as state; that is, for any given ϵ > 0, there exist a 𝒦ℒ function βc(·, ·), a 𝒦∞ function γw(·), and a parameter dc ≥ 0 such that
()

Remark 2.5. The previously mentioned stochastic small-gain theorem for jump systems is an extension of nonjump case. This extension can be achieved without any mathematical difficulties, and the proof process is the same as in [16]. The reason is that in Lemma 3.1 we only take into account the interconnection relationship between synthetical system and its subsystems, despite the fact that subsystems are of jump or nonjumpform. If both subsystems are nonjump and ISpS in probability, respectively, the synthetical system is ISpS in probability. By contraries, if both subsystems are jump and JISpS in probability, respectively, the synthetical system is JISpS in probability correspondingly.

3. Problem Description and Controller Design

3.1. Problem Description

Consider the following Markovian jump nonlinear systems with dynamic uncertainty and noise described by
()
where is state vector, u ∈ ℝ is system input signal, is unmeasured state vector, and y is output signal. is a vector of unknown adaptive parameters. The Markov chain r(t) ∈ S and Wiener noise ω are as defined in Section 2. , gi : ℝi  ×  ℝ+  ×  S → ℝl are vector-valued smooth functions, and Δi(X, ξ, t, r(t)) denotes the unmodeled dynamic uncertainty which could vary with different regime r(t) taken. Both fi, gi and Δi are locally Lipschitz as in Section 2.
Our design purpose is to find a switching controller u of the form u(x, t, k),   k ∈ S such that the closed-loop jump system could be JISpS in probability and the system output y could be within an attractive region around the equilibrium point. In this paper, the following assumptions are made for MJNS (3.1).
  •  (A1)

    The ξ subsystem with input y is JISpS in probability; namely, for any given ϵ > 0, there exist 𝒦ℒ function β(·, ·), 𝒦∞ function γ(·), and a constant dc ≥ 0 such that

    ()

  •  (A2)

    For each i = 1,2, …, n, k ∈ S, there exists an unknown bounded positive constant such that

    ()
    where , are known nonnegative smooth functions for any given k ∈ S. Notice that is not unique since any satisfies inequality (3.3). To avoid confusion, we define the smallest nonnegative constant such that inequality (3.3) is satisfied.

For the design of switching controller, we introduce the following lemmas.

Lemma 3.1 (Young’s inequality [12]). For any two vectors x, y ∈ ℝn, the following inequality holds

()
where ϵ > 0 and the constants p > 1, q > 1 satisfy (p − 1)(q − 1) = 1.

Lemma 3.2 (martingale representation [17]). Let B(t) = [B1(t), B2(t), …, BN(t)] be N-dimensional standard Wiener noise. Supposing M(t) is an -martingale (with respect to P) and that M(t) ∈ L2(P) for all t ≥ 0, then there exists a stochastic process Ψ(t) ∈ L2(P), such that

()

3.2. Controller Design

Now we seek for the switching controller for MJNS (3.1) so that the closed-loop system could be JISpS in probability, where the parameter θ*, needs to be estimated. Denote the estimation of adaptive parameter θ* with θ and the estimation of upper bound of uncertainty with pi. Perform a new transformation as
()
For simplicity, we just denote αi−1(Xi−1, t, θ, pi, k), fi(Xi, t, k), gi(Xi, t, k), Δi(X, ξ, t, k), q(y, ξ, t, k) by αi−1(k), fi(k), gi(k), Δi(k), q(k), respectively, where α0(k) = 0, αn(k) = u(k), for all k ∈ S, and the new coordinate is Z(k) = (z1(k), z2(k), …, zn(k)).
According to stochastic differential equation (2.7), one has
()
Here we define
()
From assumption (A2), one gets that there exists nonnegative smooth function ϕi1, ϕi2 satisfying
()
The inequality (3.9) could easily be deduced by using Lemma 3.1.
Considering the transformation zi in (3.7) which contains the martingale process M(t), according to Lemma 3.2, there exist a function Ψ(t) ∈ L2(P) and an N-dimensional standard Wiener noise B(t) satisfying dM(t) = Ψ(t)dB(t), where E[Ψ(t)Ψ(t)T] = ψ(t)ψ(t)T ≤ Q < ∞ and Q is a positive bounded constant. Therefore we have
()
Differential equation of new coordinate Z = (z1, z2, …, zn) is deduced by (3.10). The martingale process resulting from Markov process is transformed into Wiener noise by using Martingale representation theorem. To deal with this, quartic Lyapunov function is proposed, and in the controller design, consideration must be taken for the Wiener noise B(t).
Choose the quartic Lyapunov function as
()
where γ > 0, σi > 0 are constants. and are parameter estimation errors, where and are given positive constants.
In the view of (3.10) and (3.11), the infinitesimal generator of V satisfies
()
The following inequalities could be deduced by using Young’s inequality and norm inequalities with the help of changing the order of summations or exchanging the indices of the summations:
()
where δ0 = ∞, δn = 0 and λ > 0, μ1 > 0, μ2 > 0, δi > 0, i = 1,2, …, n are design parameters to be chosen.
Here we suggest the following adaptive laws [18]:
()
Here a > 0, , mi > 0, i = 1,2, …, n are design parameters to be chosen. And define function β(k) as
()
where εi > 0, υi > 0, i = 1,2, …, n are control parameters to be chosen, and let the virtual control signal be
()
Thus the real control signal u(k) satisfies u(k) = αn(k) such that
()
Based on assumption (A2) and (3.9), we obtain the following inequality by applying Lemma 3.1:
()
In (3.18), the following inequality is applied:
()
Notice the fact that
()
Submitting (3.18), (3.20) into (3.12), there is
()
Here parameter α1, dz and 𝒦∞ function Vξ(|ξ | , k) is chosen to satisfy
()

4. Stochastic Stability Analysis

Theorem 4.1. Considering the MJNS (3.1) with Assumptions (A2)  standing, the X-subsystem is JISpS in probability with the adaptive laws (3.14) and switching control law (3.16) adopted; meanwhile all solutions of closed-loop X-subsystem are ultimately bounded.

Proof. Considering the MJNS (3.1) with Lyapunov function (3.11), the following equations hold according to [10]:

()
Thus (3.21) can be written as
()
where positive scalar α is given as
()
It is easily seen that χ(|ξ(t)|) is a 𝒦∞ function with r(t) given, and appropriate control parameter ci, l · γ, m · σi can be chosen to satisfy α > 0.

For each integer h ≥ 1, define a stopping time as

()
Obviously, τh → ∞ almost surely as h → ∞. Noticing that 0<|z(t)| ≤ h if 0 ≤ t < τh, we can apply the generalized formula to derive that for any t ≥ 0,
()
Let h → ∞, apply Fatou’s lemma to (4.5), and we have
()
By using mean value theorem for integration, there is
()
According to the property of 𝒦∞ function, the following inequality is deduced:
()
According to (3.11), one gives
()
Consequently,
()
Defining 𝒦ℒ function β(·, ·), 𝒦∞ function γ(·), and nonnegative number dc as:
()
and applying Chebyshev’s inequality, we have that the X-subsystem of MJNS (3.1) is JISpS in probability.

The proof is completed.

Theorem 4.2. Considering the MJNS (3.1) with Assumptions (A1), (A2) holding, the interconnected Markovian jump system is JISpS in probability with adaptive laws (3.14) and switching control law (3.16) adopted; meanwhile all solutions of closed-loop system are ultimately bounded. Furthermore, the system output could be regulated to an arbitrarily small neighborhood of the equilibrium point in probability within finite time.

Proof. From Assumption (A1), the ξ subsystem is JISpS in probability. And it has been shown in Theorem 4.1 that the X subsystem is JISpS in probability. Similar to the proof in [12], we have that the entire MJNS (3.1) is JISpS in probability; that is, for any given ϵ > 0, there exists T > 0 and δ > 0 such that if t > T, the output of jump system y satisfies

()
Meanwhile δ can be made as small as possible by appropriate control parameters chosen.

5. Simulation

With loss of generality, in this section we consider a two-order Markovian jump nonlinear system with regime transition space S = {1,2}, and the system with unmodeled dynamics and noise is as follows:
()
where the transition rate matrix is with stationary distribution ζ1 = ζ2 = 0.5.
Here let noise covariance be E{dωdωT} = 1 and system dynamics for each mode as
()
From Assumption (A2), we have
()
where and and the ξ subsystem satisfies
()
where V0 = (1/2)ξ2, χ0(|x1|) = 0.15 | x1|2, d0 = 0.125, and it can be checked which satisfies the stochastic small-gain theorem. Thus the control law is taken as follows (here δ1 = 1 ).

Case 1. The system regime is k = 1:

()

Case 2. The system regime is k = 2:

()
In computation, we set the initial value to be x1 = 1.6, x2 = −2.7, θ = 0, p1 = p2 = 0 let parameter θ0 = 1, γ = 1, a = 1, p0 = 0.7, ϵi = vi = 0.5, mi = 1, μ1 = μ2 = 1 and the time step to be 0.05 s. For comparison, two groups of different control parameters are given. First we take the parameter with values c1 = c2 = 0.7, σ1 = σ2 = 2, and the simulation results are as follows. Figure 2 shows the regime transition of the jump system, Figure 3 shows the system output y which is defined as the system state x1, and Figure 4 shows system state x2. Figure 5 shows the corresponding switching controller u; finally Figure 6 shows the trajectory of adaptive parameter θ and Figure 7; Figure 8 shows the trajectory of parameter p1, p2, respectively.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Regime transition r(t).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
System output y.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
System state x2.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Switching controller u.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Adaptive parameter θ.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Parameter p1.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Parameter p2.

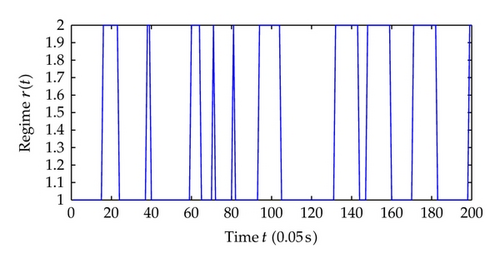
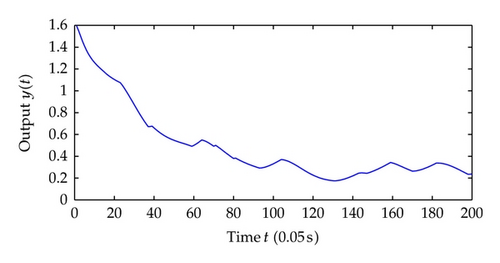
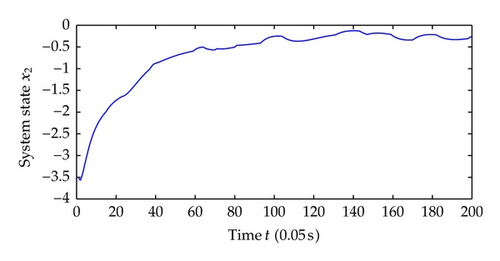
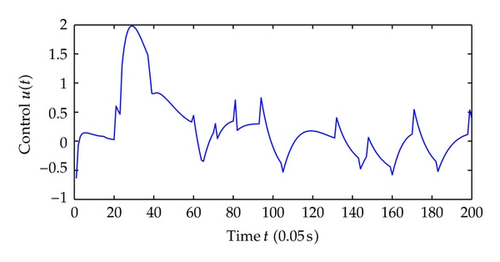
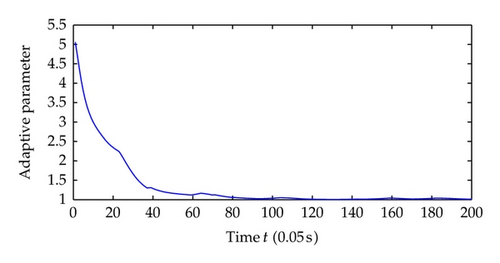
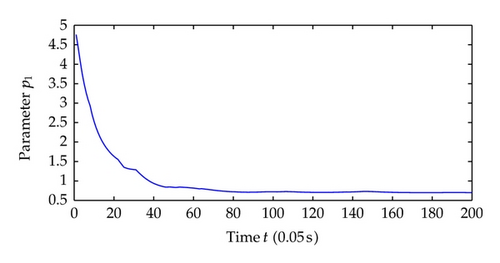
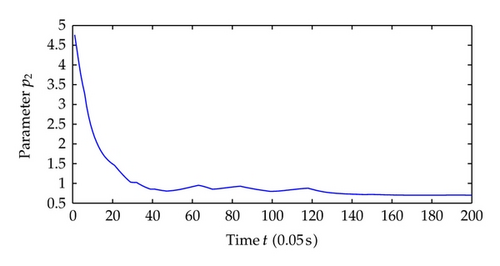
Now we choose different control parameters as c1 = c2 = 2, σ1 = σ2 = 5 and repeat the simulation. The simulation results are as follows. Figure 9 shows the regime transition of the jump system, Figure 10 shows the system output y which is defined as the system state x1 and, Figure 11 shows system state x2, and Figure 12 shows the corresponding switching controller u; the trajectory of adaptive parameter θ is shown in Figures 13 and 14; Figure 15 shows the trajectory of parameter p1, p2, respectively.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Regime transition r(t).
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
System output y.
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
System state x2.
Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
Switching controller u.
Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
Adaptive parameter θ.
Details are in the caption following the image
Figure 14
Open in figure viewerPowerPoint
Parameter p1.
Details are in the caption following the image
Figure 15
Open in figure viewerPowerPoint
Parameter p2.

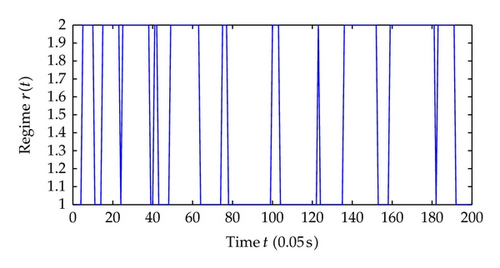
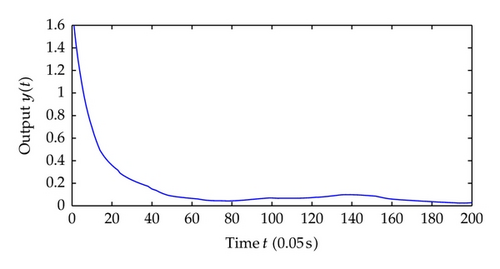
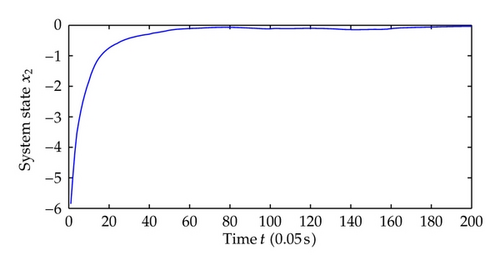
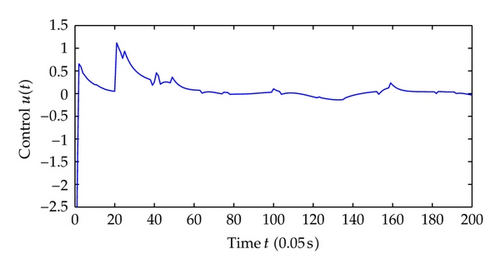
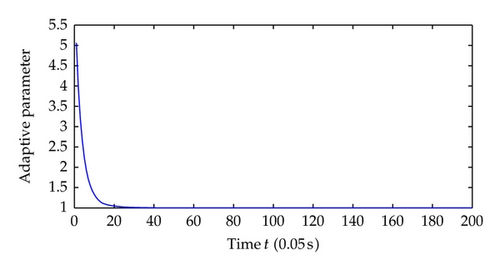
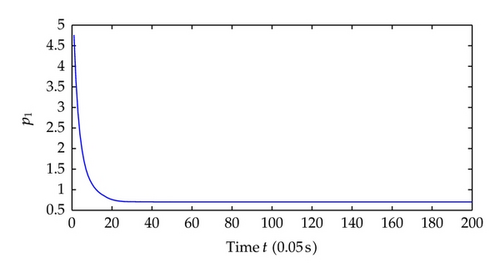
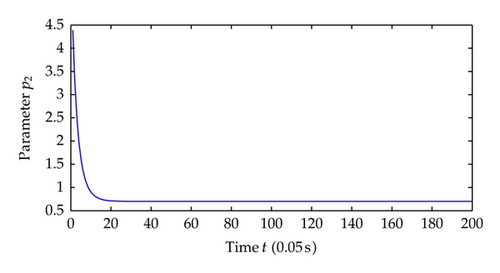
Comparing the results from two simulations, all the signals of closed-loop system are globally uniformly ultimately bounded, and the system output can be regulated to a neighborhood near the equilibrium point despite different jump samples. As could be seen from the figures, larger values of c1, c2, σ1, σ2 help to increase the convergence speed of system states. This reason is that the increase of these parameters increases the value of α, which determines the system states convergence speed. Also adaptive parameters θ and p1, p2 approach convergence faster with the increasing of aforementioned parameters.

Remark 5.1. Much research work has been performed towards the study of nonlinear system by using small-gain theorem [16, 19]. In contrast to their contributions, this paper considers a more general form than nonjump systems. The controller u(k) varies with different regime r(t) = k taken, and it differs in two aspects (see (3.16)): the coupling of regimes πkjαi−1(j) and , which are both caused by the Markovian jumps. The switching controller will degenerate to an ordinary one if r(t) ≡ 1. This controller design method can also be applied for the nonjump nonlinear system.

6. Conclusion

In this paper, the robust adaptive switching controller design for a class of Markovian jump nonlinear system is studied. Such MJNSs, suffering from unmodeled dynamics and noise of unknown covariance, are of the strict feedback form. With the extension of input-to-state stability (ISpS) to jump case as well as the small-gain theorem, stochastic Lyapunov stability criterion is put forward. By using backstepping technique, a switching controller is designed which ensures the jump nonlinear system to be jump ISpS in probability. Moreover the upper bound of uncertainties can be estimated, and system output will converge to an attractive region around the equilibrium point, whose radius can be made as small as possible with appropriate control parameters chosen. Numerical examples are given to show the effectiveness of the proposed design.

Acknowledgment

This work is supported by the National Natural Science Foundation of China under Grants 60904021 and the Fundamental Research Funds for the Central Universities under Grants WK2100060004.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.