We study the effects of control domain position on optimal control problem of cardiac arrhythmia. The well-established mathematical model, namely, the monodomain model, is used to represent the electrical behavior of the cardiac tissue. Two test cases are considered in this paper: the control domain for Test Case 1 is close to the excitation domain, while the control domain for Test Case 2 is a little bit far away from the excitation domain. The modified Dai-Yuan nonlinear conjugate gradient method is employed for computing the optimal applied extracellular current. Our experiment results show that the excitation wavefronts are successfully dampened out for both test cases. Also, experiment results show that the position of the control domain for Test Case 1 is preferable than that of Test Case 2 during the defibrillation process.

1. Introduction

Cardiac arrhythmia refers to the condition in which normal heart rhythm is disrupted. During arrhythmia, the heart may beat too rapidly, too slowly, or even irregularly. This abnormal and irregular heart rhythm causes the heart muscle to fibrillate and stops pumping blood to the body and the brain. Eventually, death can occur within minutes unless the normal heart rhythm is restored. For prevention of this sudden cardiac death, the only effective therapy is through electrical defibrillation [1–3].

The optimal control approach to cardiac arrhythmia was first proposed by Nagaiah et al. [4] with the control objective being dampen the excitation wavefront of the transmembrane potential using optimal applied extracellular current. Since the monodomain model is chosen by Nagaiah et al. [4] for representing the electrical behavior of the cardiac tissue, we, therefore, call it optimal control problem of monodomain model in the rest of the paper.

The optimal control problem of monodomain model is a PDE-constrained optimization problem that is constrained by the monodomain model. The monodomain model is a well-established mathematical model extensively used for simulation of cardiac electrical activity [5–7]. It consists of a parabolic partial differential equation (PDE) coupled to a system of nonlinear ordinary differential equations (ODEs) representing cell ionic activity.

Three classical nonlinear conjugate gradient methods have been employed by Nagaiah et al. [4] for solving the optimal control problem of monodomain model, namely, the Dai-Yuan (DY) method [8], the Hager-Zhang (HZ) method [9], and the Polak-Ribière-Polyak (PRP) method [10, 11]. Later, the optimal control problem of monodomain model has been subsequently studied by researchers with attempt to develop efficient numerical solving techniques [12–14].

Recently, the effects of the size of the control domain on the optimal control problem of monodomain model have been studied by Ng and Rohanin [15]. Two test cases with different sizes of the control domain are considered, and their numerical results show that higher extracellular current is required in the dampening process when the size of the control domain changed to a smaller one. Also, longer time is needed to dampen out the excitation wavefront when small size control domain is used.

In this paper, we are concerned with the effects of the control domain position on the optimal control problem of monodomain model. Again, two test cases are considered with each one of them located at different positions. The indirect method, also known as the optimize-then-discretize approach is used to discretize the optimal control problem. The discretized optimal control problem is then solved by the modified nonlinear conjugate gradient method, namely, the modified Dai-Yuan (MDY) method. As shown in [13], the MDY method is well performed under Armijo line search.

The outline of this paper is as follows. In Section 2, we introduce the optimal control problem of monodomain model with Rogers-modified FitzHugh-Nagumo ion kinetic. In Section 3, we present the numerical approach used to discretize the optimal control problem. In Section 4, we discuss the optimization procedure used to solve the discretized optimal control problem. In Section 5, we present and compare the experiment results for both test cases. In Section 6, we conclude our paper with a short discussion.

2. Optimal Control Problem of Monodomain Model

Let T be the final simulation time, Ω ⊂ ℜ² the computational domain with Lipschitz boundary ∂Ω, Ω_c ⊂ Ω the control domain, and Ω_o ⊂ Ω the observation domain. We further set H = Ω × [0, T] and ∂H = ∂Ω × [0, T]. The optimal control problem of monodomain model with Rogers-modified FitzHugh-Nagumo ion kinetic can be summarized as follows:

()

where

()

Here, α is the regularization parameter, η is the outer normal to Ω, D_i is the intracellular conductivity tensor, λ is the constant scalar used to relate the intracellular and extracellular conductivity tensors, β is the surface-to-volume ratio of the cell membrane, C_m is the membrane capacitance, V_th is the threshold potential, V_p is the plateau potential, c₁, c₂, c₃, and c₄ are positive parameters, V(x, t) is the transmembrane potential, w(x, t) is the ionic current variable, I_e(x, t) is the extracellular current density stimulus, I_ion(V, w) is the current density flowing through the ionic channels, and f(V, w) is the prescribed vector-value function.

Note that (2.1) is the cost functional, in which the transmembrane potential V and the ionic current variable w act as the state variables and the extracellular current I_e acts as the control variable. Also, the control variable I_e is restricted to be nontrivial only on the control domain Ω_c. The monodomain model, as defined in (2.2), appears as the PDE constraints in the optimal control problem of monodomain model. Next, the boundary and initial conditions for this optimal control problem are given in (2.3), and, lastly, (2.4) is taken from the Rogers-modified FitzHugh-Nagumo model [16].

3. Discretization of the Optimal Control Problem

The optimal control problem of monodomain model is discretized using the optimize-then-discretize approach, where the infinite dimensional first-order optimality system is derived first and the resulting optimality system is then discretized. Let p(x, t) and q(x, t) denote the adjoint variables used to enforce the constraints. Define the Lagrange functional ℒ as

()

The first-order optimality system for this optimal control problem is given by:

()

where [·]_* denotes the partial derivative with respect to * and V|_o denotes the transmembrane potential in Ω_o. Here, (3.2) is known as the state equations, (3.3) is known as the adjoint equations and (3.4) is known as the optimality condition. We further obtain the boundary and terminal conditions as follows:

()

Next, the state system can be formed using the boundary and initial conditions in (2.3) as well as the state equations in (3.2). As a result, the state system is given by

()

On the other hand, the adjoint system can be formed using the adjoint equations in (3.3) as well as the boundary and terminal conditions in (3.5). Thus, the adjoint system is given by

()

Kunisch and Wagner [17] proved that the control-to-state mapping is well defined for the optimal control problem of monodomain model, that is, C∋I_e ↦ (V(I_e), w(I_e)). Thus, the cost functional in (2.1) may be rewritten as

()

From the previous analysis, one can shows that the gradient of

is given by

()

Clearly, the optimality condition in (3.4) serves as the reduced gradient in (3.9) for our computation. As a result, the first-order optimality system consists of the state system in (3.6), the adjoint system in (3.7), and the reduced gradient in (3.9).

Notice that the state and adjoint systems in (3.6) and (3.7) consist of a parabolic PDE coupled to a system of nonlinear ODEs. Consequently, these systems are computationally demanding. In order to overcome this difficulty, the operator splitting technique [18] is applied to (3.6) and (3.7) for decomposing the complex systems into subsystems. Eventually, the state system becomes

()

and the adjoint system becomes

()

In order to complete the optimize-then-discretize approach, the first-order optimality system needs to be discretized. The linear PDEs in (3.10) and (3.11) are discretized using Galerkin finite element method in space and Crank-Nicolson method in time. For time discretization of the nonlinear ODEs in (3.10) and (3.11), a forward Euler method is used. The discretized state system is, therefore, given by

()

and the discretized adjoint system is given by

()

Here, n is the time index, Δt₁ and Δt₂ are the local time steps, M is the mass matrix, K is the stiffness matrix, and V, V|_o, p, q,w, f, I_ion, and I_e are the vectors of the same size.

4. Optimization Procedure

In this paper, we adopt the modified nonlinear conjugate gradient method, namely, the modified Dai-Yuan (MDY) method as proposed by Zhang [19] for solving the discretized optimal control problem of monodomain model. Starting from an initial guess

, the control variable is updated using the following recurrence:

()

where δ^k > 0 is the step length computed by the Armijo line search and d^k is the search direction generated by

()

where

is the conjugate gradient update parameter given by

()

where

()

Recall that the step length δ^k is computed by the Armijo line search. Given an initial step length δ > 0 and μ, ρ ∈ (0,1), the Armijo line search choose, δ^k = max {δ, δρ, δρ², …} such that

()

Consequently, the optimization algorithm for the MDY method can be summarized as follows.

4.1. Optimization Algorithm

Step 1. Provide an initial guess and set k = 0.

Step 2. Solve the discretized state system in (3.12) for time interval [0, T] as follows.

(a)
Solve the linear PDE for t ∈ [t, t + Δt/2]
()
(b)
Solve the nonlinear ODEs for t ∈ [t, t + Δt]
()
(c)
Solve the linear PDE for t ∈ [t + Δt/2, t + Δt]
()
where Δt is the global time step.

Step 3. Evaluate the reduced cost functional .

Step 4. Solve the discretized adjoint system in (3.13) for time interval [T, 0] as follows.

(a)
Solve the linear PDE for t ∈ [T, T − Δt/2]
()
(b)
Solve the nonlinear ODEs for t ∈ [T, T − Δt]
()
(c)
Solve the linear PDE for t ∈ [T − Δt/2, T − Δt]
()

Step 5. Update the reduced gradient using (3.9).

Step 6. For k ≥ 1, check the following stopping criteria:

()

If one of them is met, stop.

Step 7. Compute the conjugate gradient update parameter using (4.3).

Step 8. Compute the search direction d^k using (4.2).

Step 9. Compute the step length δ^k that satisfies the condition in (4.5).

Step 10. Update the control variable using (4.1). Set k = k + 1 and go to Step 2.

5. Numerical Experiments

5.1. Experiment Setup

A two-dimensional computational domain of size 1 × 1 cm², that is, Ω = [0,1] × [0,1] is considered in our numerical experiments, and the final simulation time is set to be T = 2 ms. Figure 1 displays the positions of the subdomains in the computational domain Ω for Test Case 1 and Test Case 2. As shown in the figures, Ω_c1 and Ω_c2 are the control domains, and are the neighborhoods of the control domains, is the observation domain, and Ω_exi ⊂ Ω_o is the excitation domain where the cardiac arrhythmia first occurs.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Computational domain Ω and its subdomains for (a) Test Case 1 and (b) Test Case 2.

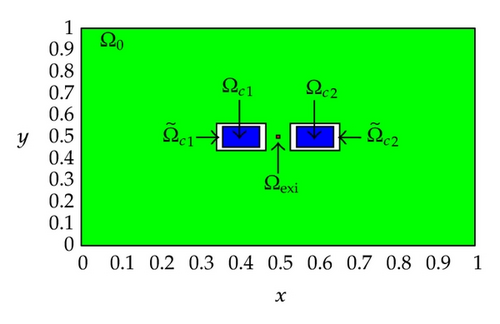
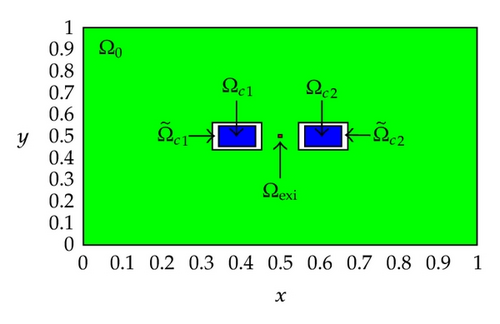
Also, observe that the control domain for Test Case 1 is close to the excitation domain while the control domain for Test Case 2 is a little bit far away from the excitation domain. These positions of the control domain are purposely set for studying the effects of the control domain position on the optimal control problem of monodomain model. In our numerical experiments, the control domain might corresponds to the electrodes of the implantable cardioverter defibrillator (ICD) implanted in the chest of patients who are at significant risk of sudden cardiac death. More specifically, we are trying to locate a better position for implanting the electrodes of the ICD to ensure a successful and efficient defibrillation.

Table 1 lists the parameters that are used in our numerical experiments, with some of them adopted from Franzone et al. [20]. Moreover, the initial values for V, w, I_e are given as

()

As shown in (5.3), the initial value for the control variable is set to be zero in the control domain. Meaning that no extracellular current is applied to the patient at the beginning of the numerical experiments.

Table 1. Parameters used in the numerical experiment.

Parameter	Value	Units
β	10³	cm⁻¹
C_m	10⁻³	mF cm⁻²
	3 × 10⁻³	S cm⁻¹
	3.1525 × 10⁻⁴	S cm⁻¹
V_th	1.3 × 10¹	mV
V_p	10²	mV
c₁	1.5	mS cm⁻²
c₂	4.4	mS cm⁻²
c₃	1.2 × 10⁻²	ms⁻¹
c₄	1	Dimensionless
α	10⁻⁴	Dimensionless
λ	7.062 × 10⁻¹	Dimensionless
δ	1	Dimensionless
μ	10⁻⁴	Dimensionless
ρ	10⁻¹	Dimensionless
Δt	0.1	ms
Δt₁	2.5 × 10⁻²	ms
Δt₂	10⁻³	ms

5.2. Experiment Results

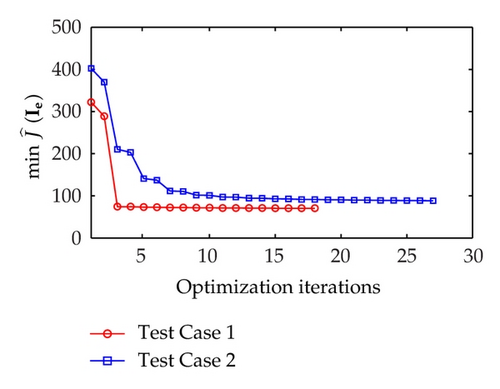
The minimum values of the reduced cost functional and the corresponding norm of reduced gradient along the optimization process for Test Case 1 and Test Case 2 are depicted in Figure 2. As shown in the figures, Test Case 1 and Test Case 2 successfully converge to the optimal solution by taking 18 and 27 optimization iterations. Also, observe that the minimum value for Test Case 1 is lower than that one for Test Case 2. This result implies that when the control domain is relocated to a position which is far away from the excitation domain, more iteration is needed for the MDY method to converge to the optimal solution.

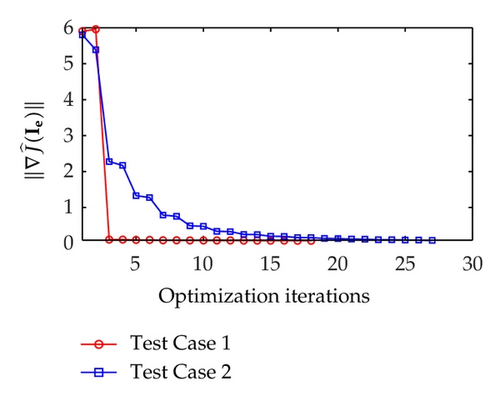
As illustrated in Figure 2, the reduced gradient for Test Case 1 decreased sharply at iteration 3, followed by a smooth decrease till the end of optimization iterations. On the other hand, the reduced gradient for Test Case 2 decreases less sharply than that of Test Case 1 at iteration 3 and slowly approaches zero with a smooth decrease.

Figure 3 illustrates the uncontrolled solutions for the optimal control problem of monodomain model at times 0.2 ms, 0.8 ms, 1.5 ms, and 2.0 ms. Notice that the uncontrolled solutions are obtained by setting the control variable equal to zero at the control domain as well as at the outside of the control domain, that is, I_e = 0 for x ∈ Ω. As shown in the figures, the excitation wavefront spreads from the excitation domain to the nearby computational domain during the time interval from 0 ms to 2 ms. This result implies that if no extracellular current (I_e) is applied to the control domain, the excitation wavefront will continue to spread to the entire computational domain.

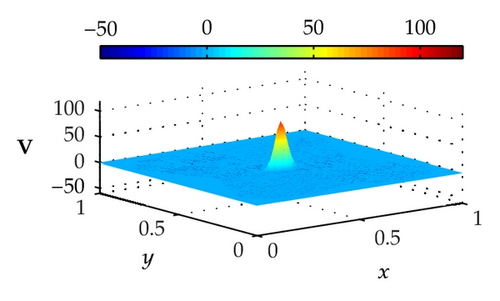
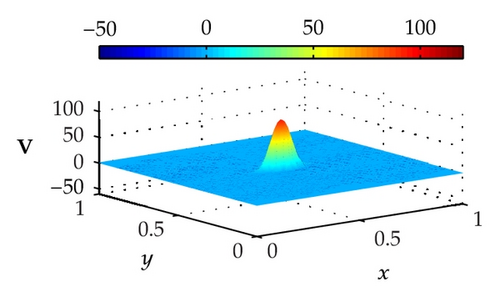
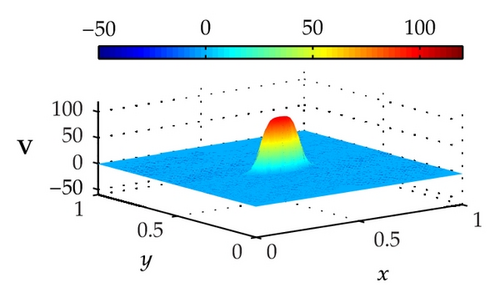
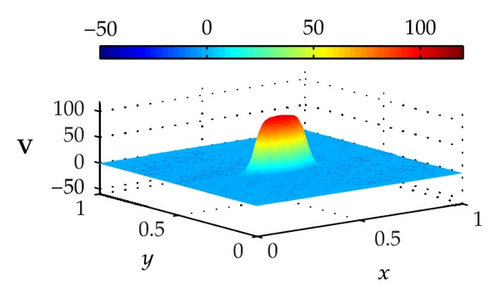
Figure 4 illustrates the optimally controlled solutions for Test Case 1 at times 0.2 ms, 0.8 ms, 1.5 ms, and 2.0 ms. As shown in the figures, the excitation wavefront is successfully dampened out by the optimal extracellular current . Note that the excitation wavefront is almost completely dampened out at time 1.5 ms. Next, Figure 5 depicts the optimally controlled solutions for Test Case 2 at times 0.2 ms, 0.8 ms, 1.5 ms, and 2.0 ms. Again, the excitation wavefront is successfully dampened out by . Observe that at time 1.5 ms, the excitation wavefront is still not completely dampened out. Thus, by comparison to Test Case 1, longer time is needed for Test Case 2 to dampen out the excitation wavefront.

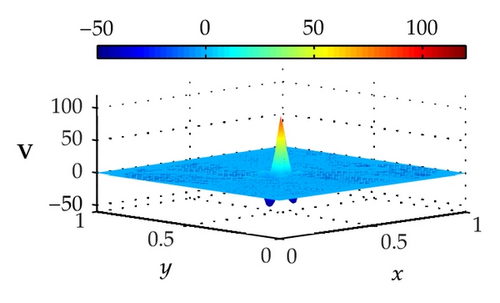
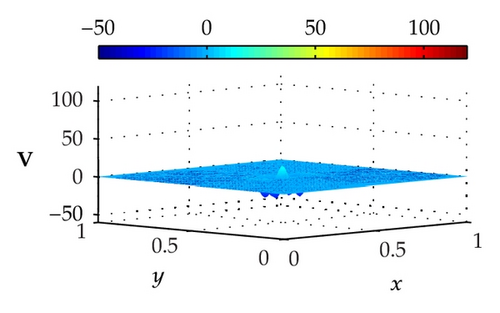
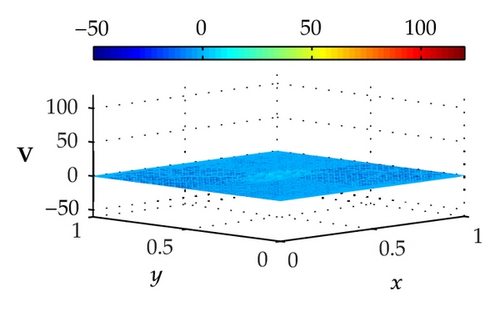
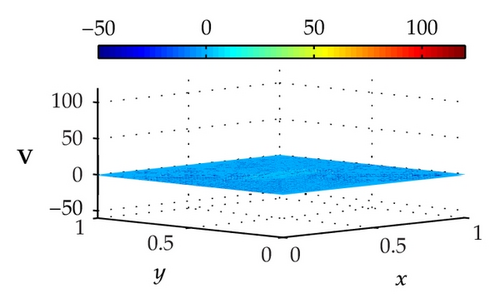
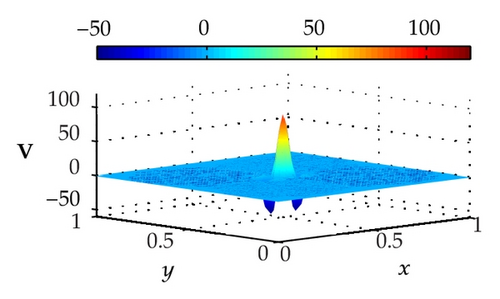
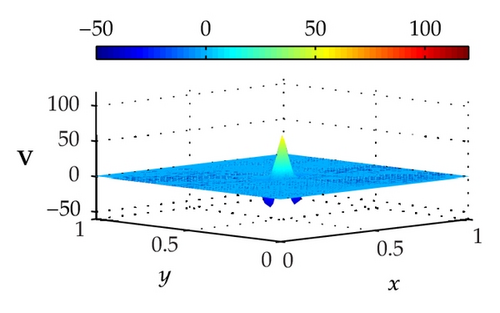
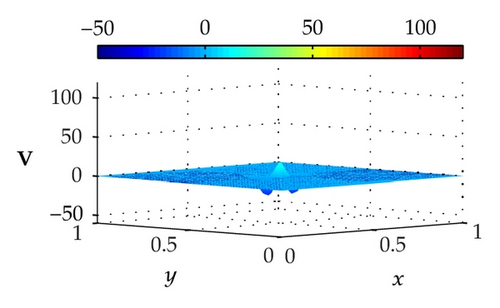
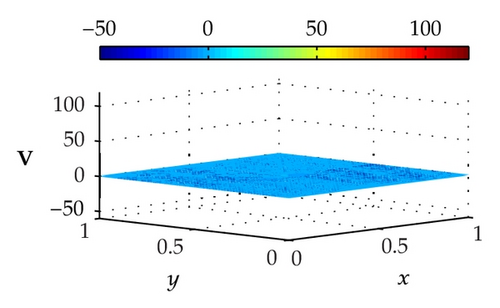
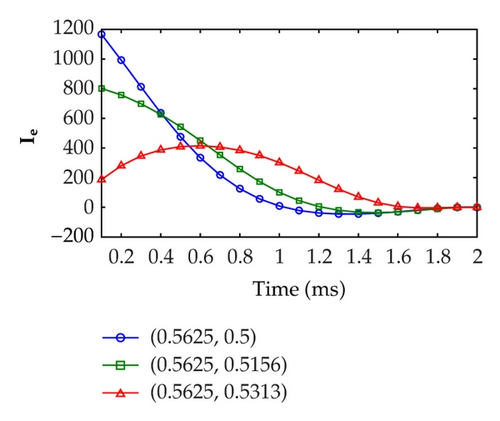
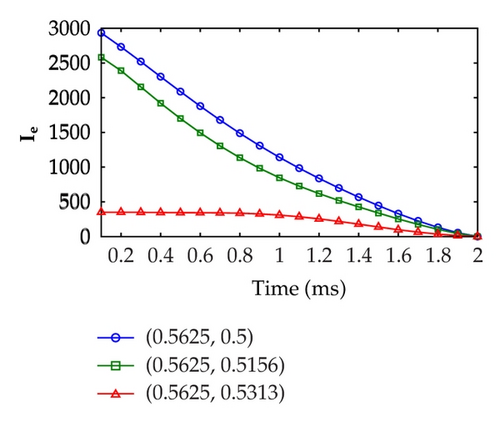
Figure 6 displays the optimal extracellular current at three fixed points, that is, (x₁, y₁) = (0.5625,0.5), (x₂, y₂) = (0.5625,0.5156), and (x₃, y₃) = (0.5625,0.5313) over the time evolution. As shown in the figures, the highest extracellular current required by Test Case 1 in the defibrillation process is around 1200 mA cm⁻³. On the other hand, the highest extracellular current required by Test Case 2 in the defibrillation process is twice as large as Test Case 1, that is, approximately 3000 mA cm⁻³. This result implies that higher extracellular current is necessary if the control domain is relocated to a position which is far away from the excitation domain.

6. Conclusions

This work studies the effects of the control domain position on the optimal control problem of cardiac arrhythmia by using two test cases. The control domain for Test Case 1 is close to the excitation domain, while the control domain for Test Case 2 is a bit further away from it. Our numerical results show that when the control domain is relocated to a position which is far from the excitation domain (as demonstrated by Test Case 2), more iteration is needed for the MDY method to converge to the optimal solution. Numerical results also show that longer time is needed by Test Case 2 for dampening out the excitation wavefront. Moreover, if the control domain is far from the excitation domain, higher extracellular current is required during the defibrillation process in order to dampen out the excitation wavefront. Thus, if we know which part of the heart of the patient is frequently suffering from cardiac arrhythmia, the electrodes of the implantable cardioverter defibrillator (ICD) should be implanted close to that part for improving the performance of the defibrillation process.

Acknowledgments

The work is financed by Zamalah Scholarship and Research University Grant (GUP) Vote 06J26 provided by Universiti Teknologi Malaysia and the Ministry of Higher Education of Malaysia.

References

1 Amann A., Tratnig R., and Unterkofler K., A new ventricular fibrillation detection algorithm for automated external defibrillators, Computers in Cardiology. (2005) 32, 559–562, 2-s2.0-33846402235, https://doi.org/10.1109/CIC.2005.1588162.
10.1109/CIC.2005.1588162
Google Scholar
2 Dosdall D. J., Fast V. G., and Ideker R. E., Mechanisms of defibrillation, Annual Review of Biomedical Engineering. (2010) 12, 233–258, 2-s2.0-77955629578, https://doi.org/10.1146/annurev%2Dbioeng%2D070909%2D105305.
10.1146/annurev-bioeng-070909-105305
CAS PubMed Web of Science® Google Scholar
3 Klein R. C., Raitt M. H., Wilkoff B. L., Beckman K. J., Coromilas J., Wyse D. G., Friedman P. L., Martins J. B., Epstein A. E., Hallstrom A. P., Ledingham R. B., Belco K. M., and Greene H. L., Analysis of implantable cardioverter defibrillator therapy in the antiarrhythmics versus implantable defibrillators (AVID) trial, Journal of Cardiovascular Electrophysiology. (2003) 14, no. 9, 940–948, 2-s2.0-10744222859, https://doi.org/10.1046/j.1540%2D8167.2003.01554.x.
10.1046/j.1540-8167.2003.01554.x
PubMed Web of Science® Google Scholar
4 Nagaiah C., Kunisch K., and Plank G., Numerical solution for optimal control of the reaction-diffusion equations in cardiac electrophysiology, Computational Optimization and Applications. (2011) 49, no. 1, 149–178, 2-s2.0-79956134315, https://doi.org/10.1007/s10589%2D009%2D9280%2D3, ZBL1226.49024.
10.1007/s10589-009-9280-3
Web of Science® Google Scholar
5 Shuaiby S. M., Hassan M. A., and El-Melegy M., Modeling and simulation of the action potential in human cardiac tissues using finite element method, Journal of Communications and Computer Engineering. (2012) 2, no. 3, 21–27.
10.20454/jcce.2012.152
Google Scholar
6 Belhamadia Y., Fortin A., and Bourgault Y., Towards accurate numerical method for monodomain models using a realistic heart geometry, Mathematical Biosciences. (2009) 220, no. 2, 89–101, 2-s2.0-67650676756, https://doi.org/10.1016/j.mbs.2009.05.003, ZBL1168.92003.
10.1016/j.mbs.2009.05.003
PubMed Web of Science® Google Scholar
7 Clayton R. H. and Panfilov A. V., A guide to modelling cardiac electrical activity in anatomically detailed ventricles, Progress in Biophysics and Molecular Biology. (2008) 96, no. 1–3, 19–43, 2-s2.0-43049105439, https://doi.org/10.1016/j.pbiomolbio.2007.07.004.
10.1016/j.pbiomolbio.2007.07.004
CAS PubMed Web of Science® Google Scholar
8 Dai Y. H. and Yuan Y., A nonlinear conjugate gradient method with a strong global convergence property, SIAM Journal on Optimization. (1999) 10, no. 1, 177–182, 2-s2.0-0033266804.
10.1137/S1052623497318992
Web of Science® Google Scholar
9 Hager W. W. and Zhang H., A new conjugate gradient method with guaranteed descent and an efficient line search, SIAM Journal on Optimization. (2005) 16, no. 1, 170–192, 2-s2.0-33144465578, https://doi.org/10.1137/030601880.
10.1137/030601880
Web of Science® Google Scholar
10 Polak E. and Ribière G., Note sur la convergence de méthodes de directions conjuguées, Revue Française d′Informatique et de Recherche Opérationnelle. (1969) 16, 35–43, ZBL0174.48001.
10.1051/m2an/196903R100351
Google Scholar
11 Polyak B. T., The conjugate gradient method in extremal problems, USSR Computational Mathematics and Mathematical Physics. (1969) 9, no. 4, 94–112, 2-s2.0-0001931644, https://doi.org/10.1016/0041%2D5553(69)90035%2D4, ZBL0191.49003.
10.1016/0041-5553(69)90035-4
Google Scholar
12 Nagaiah C. and Kunisch K., Higher order optimization and adaptive numerical solution for optimal control of monodomain equations in cardiac electrophysiology, Applied Numerical Mathematics. (2011) 61, no. 1, 53–65, 2-s2.0-78049481393, https://doi.org/10.1016/j.apnum.2010.08.004, ZBL1201.92026.
10.1016/j.apnum.2010.08.004
Web of Science® Google Scholar
13 Ng K. W. and Rohanin A., Numerical solution for PDE-constrained optimization problem in cardiac electrophysiology, International Journal of Computer Applications. (2012) 44, no. 12, 11–15.
10.5120/6314-8655
Google Scholar
14 Ng K. W. and Rohanin A., Modified Fletcher-Reeves and Dai-Yuan conjugate gradient methods for solving optimal control problem of monodomain model, Applied Mathematics. (2012) 3, no. 8, 864–872, https://doi.org/10.4236/am.2012.38128.
10.4236/am.2012.38128
Google Scholar
15 Ng K. W. and Rohanin A., The effects of control domain size on optimal control problem of monodomain model, International Journal of Computer Applications. (2012) 47, no. 10, 6–11.
10.5120/7222-0046
Google Scholar
16 Rogers J. M. and McCulloch A. D., A collocation-Galerkin finite element model of cardiac action potential propagation, IEEE Transactions on Biomedical Engineering. (1994) 41, no. 8, 743–757, 2-s2.0-0028483993, https://doi.org/10.1109/10.310090.
10.1109/10.310090
CAS PubMed Web of Science® Google Scholar
17 Kunisch K. and Wagner M., Optimal control of the bidomain system (I): the monodomain approximation with the Rogers-McCulloch model, Nonlinear Analysis: Real World Applications. (2012) 13, no. 4, 1525–1550, https://doi.org/10.1016/j.nonrwa.2011.11.003.
10.1016/j.nonrwa.2011.11.003
Web of Science® Google Scholar
18 Qu Z. and Garfinkel A., An advanced algorithm for solving partial differential equation in cardiac conduction, IEEE Transactions on Biomedical Engineering. (1999) 46, no. 9, 1166–1168, 2-s2.0-0032845277, https://doi.org/10.1109/10.784149.
10.1109/10.784149
CAS PubMed Web of Science® Google Scholar
19 Zhang L., Two modified Dai-Yuan nonlinear conjugate gradient methods, Numerical Algorithms. (2009) 50, no. 1, 1–16, 2-s2.0-61849163301, https://doi.org/10.1007/s11075%2D008%2D9213%2D8, ZBL1173.65046.
10.1007/s11075-008-9213-8
CAS Web of Science® Google Scholar
20 Franzone P. C., Deuflhard P., Erdmann B., Lang J., and Pavarino L. F., Adaptivity in space and time for reaction-diffusion systems in electrocardiology, SIAM Journal on Scientific Computing. (2006) 28, no. 3, 942–962, 2-s2.0-34249063270, https://doi.org/10.1137/050634785, ZBL1114.65110.
10.1137/050634785
Web of Science® Google Scholar

All articles

The Effects of Control Domain Position on Optimal Control of Cardiac Arrhythmia

Abstract

1. Introduction

2. Optimal Control Problem of Monodomain Model

3. Discretization of the Optimal Control Problem