Volume 2012, Issue 1 457603

Research Article

Open Access

Nonsmooth Recursive Identification of Sandwich Systems with Backlash-Like Hysteresis

Ruili Dong,

Ruili Dong

College of Mechanical and Electronic Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Yonghong Tan,

Corresponding Author

Yonghong Tan

[email protected]

College of Mechanical and Electronic Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Hui Chen,

Hui Chen

Department of Automation, Southeast University, Nanjing 210096, China seu.edu.cn

Search for more papers by this author

Yangqiu Xie,

Yangqiu Xie

School of Electronic Engineering, Xi’dian University, Xi’an 710071, China xidian.edu.cn

Search for more papers by this author

Ruili Dong,

Ruili Dong

College of Mechanical and Electronic Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Yonghong Tan,

Corresponding Author

Yonghong Tan

[email protected]

College of Mechanical and Electronic Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Hui Chen,

Hui Chen

Department of Automation, Southeast University, Nanjing 210096, China seu.edu.cn

Search for more papers by this author

Yangqiu Xie,

Yangqiu Xie

School of Electronic Engineering, Xi’dian University, Xi’an 710071, China xidian.edu.cn

Search for more papers by this author

First published: 15 July 2012

https://doi.org/10.1155/2012/457603

Citations: 1

Academic Editor: Zhiwei Gao

Share a link

Email
Wechat
Bluesky

Abstract

A recursive gradient identification algorithm based on the bundle method for sandwich systems with backlash-like hysteresis is presented in this paper. In this method, a dynamic parameter estimation scheme based on a subgradient is developed to handle the nonsmooth problem caused by the backlash embedded in the system. The search direction of the algorithm is estimated based on the so-called bundle method. Then, the convergence of the algorithm is discussed. After that, simulation results on a nonsmooth sandwich system are presented to validate the proposed estimation algorithm. Finally, the application of the proposed method to an X-Y moving positioning stage is illustrated.

1. Introduction

Usually, a sandwich system with backlash-like hysteresis is defined as the system that a backlash-like hysteresis is sandwiched between two linear dynamic subsystems. In engineering applications, many mechanical systems such as mechanical transmission systems, servo control systems, and hydraulic valve systems can be described by the so-called sandwich systems with backlash-like hysteresis. The reason to cause the backlash-like hysteresis phenomenon is mainly due to the gaps existing in transmission mechanism systems such as gearbox and ball screw.

Recently, identification of sandwich systems has become one of the interesting issues in the domain of modeling and control for complex systems. References [1–3] proposed the recursive identification methods for the sandwich system with smooth nonlinearities. The main ideas of those approaches are to extend the linear system identification methods to smooth nonlinear cases. Moreover, there have been some methods for the identification of Hammerstein or Wiener systems with backlash-like hysteresis [4–8], most of which are the modified linear system identification methods.

However, until today, there have been very few publications concerning the identification of the sandwich systems with backlash-like hysteresis. Reference [9] proposed a method to identify the sandwich systems with backlash-like hysteresis, but the approach is still based on idea to extend the linear system identification method to nonlinear cases. On the other hand, the switching functions in that method have significant influence on the convergence speed of the algorithm.

In this paper, a recursive gradient algorithm based on the bundle method is proposed to identify parameters of the sandwich model. In this algorithm, the effect of the nonsmoothness caused by the backlash-like hysteresis in sandwich system is considered. In order to obtain the optimizing search direction at the nonsmooth points of the system, the Clarke subgradient technique is utilized based on the idea of the bundle method [10–12]. By comparing with the above-mentioned available methods, the proposed method employs the nonsmooth optimization technique to identify the nonsmooth sandwich systems with backlash-like hysteresis. Thus, it will provide us with a new approach for dealing with on-line modeling of nonsmooth dynamic systems. A numerical example will be presented to evaluate the performance of the proposed approach. Finally, experimental results on an X-Y moving positioning stage are illustrated.

2. Brief Description of Sandwich Systems with Backlash

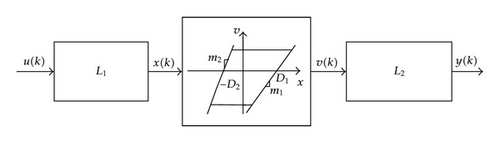
The structure of a sandwich system with backlash-like hysteresis is shown in Figure 1, in which a backlash-like hysteresis is embedded between the input and output linear subsystems, that is, L₁(·) and L₂(·). It is assumed that input u(k) and output y(k) can be measured directly, but the internal variables x(k) and v(k) are not measurable.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The structure of the sandwich system with backlash-like hysteresis.

Suppose that both linear subsystems are stable, and the time delays q₁ and q₂ in L₁(·) and L₂(·) are known, respectively. The corresponding discrete-time models of L₁(·) and L₂(·) are, respectively, written as

()

where n_a and n_b are the orders of L₁(·), q₁ is the time delay, and

as well as

are the coefficients of L₁(·); n_c and n_d are the orders of L₂(·), q₂ is the time delay, and

and

are the coefficients of L₂(·). Let both b₀ and d₀ be equal to unity for unique representation.

Note that the backlash-like hysteresis shown in Figure 1 is specified by the slopes m₁ and m₂ as well as the absolute thresholds, D₁ and D₂, where 0 < m₁ < ∞, 0 < m₂ < ∞, 0 < D₁ < ∞, and 0 < D₂ < ∞. Hence, the discrete-time model of the backlash-like hysteresis is described as

()

For the convenience to describe the system, the discrete-time model of the backlash-like hysteresis can be rewritten as

()

where the switching functionsg(k), g₁(k), and g₂(k) are, respectively, defined as

()

where Δx(k) = x(k) − x(k − 1).

Thus, (2.1)–(2.3) present the model to describe the sandwich system with backlash-like hysteresis. Hence, the unknown parameter vector of the model can be written as

, where

()

According to concept of the gradient algorithm, define the objective function as

()

where

is the estimate of θ, and

is the output of system model. The optimal estimate of

can be obtained by minimizing the above-mentioned criterion.

3. The Nonsmooth Estimation of the Sandwich Model with Backlash-Like Hysteresis

In this section, a gradient-based identification algorithm is proposed for identification of the sandwich system with backlash-like hysteresis. Due to the nonsmoothness of the backlash, the gradients of the system output with respect to the parameters of the backlash at nonsmooth points will not exist. The smooth gradient-based methods directly applied to nonsmooth systems may fail in convergence [13]. On the other hand, the genetic algorithms [14] or Powell’s method [15], which are based on derivative-free techniques, may be unreliable and become inefficient when the system structure is complicated. Thus, we should find a special way for solving this problem. The simplest way to solve the problem is to apply the Clarke subgradients [11] to the approximation of the gradients at the nonsmooth points.

The basic idea of the bundle method is to approximate the subdifferential of with respect to by gathering the subgradients from previous iterations into a bundle for the nonsmooth objective function . The gradient can change discontinuously, and some change of the gradient may not be small in the neighborhood of the minimum of the function. So the values of and at a single point do not offer sufficient information of the local behavior of . The detail of the bundle method can be found in [10–12] and reference therein.

Considering that the sandwich system with backlash-like hysteresis is locally Lipschitz continuous, we have the following definition.

Definition 3.1 (see [11].)Let F: Rⁿ × R → R be locally Lipschitz continuous. This allows one to define a Clarke subgradient of F at ξ as dF(ξ):

()

where “conv” denotes the convex hull of a set.

The set of all the Clarke subgradients is the Clarke subdifferential of Fat ξ which is denoted by ∂F(ξ) [11].

Considering that backlash-like hysteresis is a nonsmooth mapping, the gradients of parameters in L₁(·) with respect to v(k) do not exist at a nonsmooth point. Hence, we define the parameters of the backlash-like hysteresis and L₁(·) as . Considering the cost function described by (2.6), the gradients of f(·) with respect to σ will not exist at the nonsmooth points. Hence, at the nonsmooth points of Q(·), the Clarke subdifferential of f(·) with respect to σ, that is, ∂f(σ), can be obtained by

()

where

, and

is the gradient of

, the output of backlash-like hysteresis, with respect to σ at the smooth points. Thus, the corresponding gradients of

with respect to σ at the smooth points are

()

where

, and the coefficients

and

are the corresponding estimated values at the previous step.

Hence, based on (3.2) and (3.3), the Clarke subdifferential of f(·) with respect to σ can be obtained at nonsmooth points of the system. Besides, as L₂(·) is a smooth function, the gradients of f(·) with respect to the parameters of the linear subsystems L₂(·) always exist. So, the Clarke subdifferential of f(·) with respect to all the unknown parameters of the sandwich system can be determined.

The proper Clarke subgradient direction t of f(·) with respect to the parameters to be estimated at nonsmooth points can be derived based on

()

where ∥·∥ denotes the Euclidean norm; J_k is a nonempty subset of {1, …, k}; set φ(k) is the predicted amount of descent;

for j ∈ J_k, and

are some trail points (from the past iterations);

is the locality measure of subgradient; γ ≥ 0 is the distance measure parameter (γ = 0 if

is convex),

is the linearization error;

is the distance measure to estimate

without the requirement to store the trial point

According to formula (3.4), t(k) and φ(k) are obtained, that is,

()

where

, and

Remark 3.2. If f(·) is convex, the model is an underestimate for f(·), and the nonnegative linearization error α_j(k) measures the performance of an approximation of the model to the original cost function. If f(·) is nonconvex, these facts are not valid anymore because α_j(k) may have a small or even negative value, although the trial point locates far away from the current iteration point , and thus, the corresponding subgradient h_j(k) is worthless. For these reasons, the locality measure of subgradient β_j(k) is introduced.

Therefore, the proposed recursive gradient estimation algorithm based on bundle method for the sandwich model with backlash-like hysteresis is shown as follows.

Step 1. Select starting point and stopping parameter δ > 0. Calculate f(k, θ₀) and vector h_j(k) ∈ ∂f(k, θ₀), where j ∈ J_k, J_k = {k₀}, |J_k | ≤ k₁, |J_k| is the element number of J_k, and k₁ is a given positive number. Set β_j(k) = 0, k = k₀ and the line search parameters

()

Step 2. Calculate optimal solution based on formulas (3.2)–(3.6). If φ(k)≥−δ, then stop.

Step 3. Search for the largest step size η(k)∈[0,1] such that η(k) ≥ η(0) and if

()

it holds

()

Then, we take a long step and set

and

; go to Step 4.

Otherwise, if 0 < η(k) < η(0), and formula (3.8) holds, then we take a short step and set , and where η^*(k) > η(k). Go to Step 5.

If η(k) = 0, and formula (3.8) holds, we take a null step, and namely set and ; go to Step 5.

Step 4. Let J_k = J_k ∪ {k + 1}, k = k + 1; if k ≤ k₁, then J_k = {1, …, k}, and if k > k₁, then J_k = J_k−1 ∪ {k}∖{k − k₁}, then go to Step 2.

Step 5. J_k = J_k ∪ {k + 1}, k = k + 1; if k ≤ k₁, then J_k = {1, ⋯, k}, and if k > k₁, then J_k = J_k−1 ∪ {k}∖{k − k₁}, and the proper Clarke subgradient h_j(k) satisfies

()

then go to Step 2.

Remark 3.3. In long step, there is an obvious decrease in the value of the objective function. Hence, it is unnecessary to detect discontinuities in the gradient of f(·). Thus, we just set . On the other hand, in short steps and null steps, the gradient of f(·) is discontinuous. Then, based on (3.10), both and located on the opposite sides of this discontinuity are guaranteed, and the new subgradient h_j(k) ∈ ∂f(k, θ^*(k)) will force an obvious modification of the next search direction. Hence, the algorithm approximates the effectively searching direction at nonsmooth points based on the bundle method, which cannot be realized by the smooth optimization techniques.

Remark 3.4. If the value of η(0) is too small, the convergence speed will be very sluggish, while η(0) is too large, and the algorithm may not be convergent. Hence, it is important for η(0) to be chosen properly. Usually, η(0) is chosen based on an empirical method.

Remark 3.5. If all the Clarke subgradients are included in J_k, the corresponding storage capacity is infinite. Hence, the number of the subgradients in J_k must be constrained. In the proposed algorithm, we give the upper bound of |J_k | ≤ k₁, and the upper bound k₁ is specified by empirical method.

4. Convergence of the Estimation

For the convergence of the above-mentioned estimation algorithm, we have the following

Theorem 4.1. Suppose that η(k) and β_j(k) satisfy

()

respectively, then the parameters θ can be convergent to a local optimal value.

Proof. The proof of this theorem can be found in Appendix.

5. Simulation

The proposed approach is used to identify a numerical sandwich system with backlash-like hysteresis based on the measured system input and output. Suppose that the parameters of the backlash-like hysteresis in the system are m₁ = 1, m₂ = 1.2, D₁ = 0.5, and D₂ = 0.6. The linear subsystems L₁(·) and L₂(·) are

()

respectively.

That implies a₁ = 0.1, a₂ = 0.2, b₀ = 1.5, c₁ = 1.2, c₂ = 0.32, d₀ = 2, and d₁ = −0.1. In the simulation, both b₀ and d₀ are assumed to be equal to unity for model uniqueness, which implies that the corresponding equivalent true values of the coefficients are , , , , , , , , and , respectively, but this does not affect the properties of the whole system.

In the simulation, the signal to excite the system is a random sequence with variance σ² = 0.49. Choose δ = 1.0 × 10⁻⁴. In the proposed algorithm, based on Remark 3.4, select η(0) = 0.015, k₁ = 6, θ₀ = [0, 0, 0, 0, 0.1,0.1,0.1,0.1, 0] ^T, and β₁(k₀) = 0, respectively. For comparison, the traditional gradient method is also used to estimate the parameters of the system. In this method, the nonsmooth points of the system are omitted for the gradients of the system do not exist at nonsmooth points. The initialized values of the parameters are the same as those used in the proposed method. The optimizing step is chosen as 0.009.

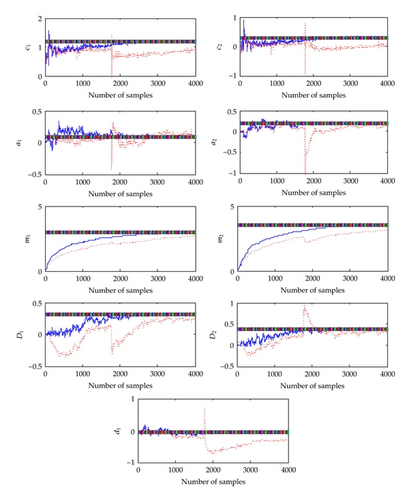
Figure 2 illustrates the comparison of the estimated parameter convergence procedures between the proposed method and the traditional gradient method. In Figure 2, blue and solid lines denote the convergence procedures of the parameters estimated by the proposed method, while red and dotted lines show the convergence procedures of the parameters determined by the traditional gradient method. From Figure 2, we note that the parameters of the backlash-like hysteresis converge slower than those of the linear submodels especially the input linear submodel. Moreover, the proposed method has achieved faster convergence than that of the traditional gradient method. It is noticed that the oscillation and sharp jumps happened in the estimation procedure of the traditional gradient approach.

In the case that the system is affected by random noise, the proposed strategy can still obtain better convergence of parameter estimation. In the simulation with noise, the signal to noise rate (SNR) is equal to 46.5. All the initial values of the parameters are the same as those in the noise-free case.

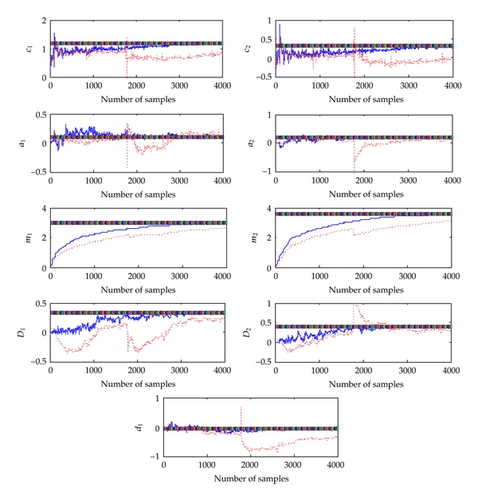
Figure 3 shows the comparison of the convergence procedures of the estimated parameters in the case with noise between the proposed method and the traditional gradient approach. Similar to the noise-free case, the blue and solid lines denote the convergence procedures of the parameters estimated by the proposed method, while the red and dotted lines show the convergence procedures of the parameters estimated by the traditional gradient method. Obviously, the proposed method has obtained faster convergent results than the traditional gradient method.

6. Application to an X-Y Moving Positioning Stage

The proposed identification approach is also applied to the modeling of an X-Y moving positioning stage with the architecture shown in Figure 4. In this equipment, the movement of the work platform of each axis is driven by a DC servomotor through a ball-screw-nut mechanism which transforms the rotational shaft movement into linear displacement. The servomotor is controlled by a digital signal processor (TMS320LF-2407A). The displacement of each axis is measured by a linear encoder (RGF2000H125B). The signals of both phase A and phase B encoders are decoded by a quadrature decoding circuit which is based on the decoding chip (Agilent HCTL-2020).

In this system, the servomotor can be considered as a second-order linear dynamic subsystem. The movement of the work platform is also described by a linear second-order dynamic model. Due to the inherent characteristic, both dead zone and backlash-like hysteresis exist in this system. In order to simplify the identification procedure, the dead zone is compensated by a dead zone inverse model-based compensator. Thus, in the identification, only the effect of backlash-like hysteresis existing in the ball-screw-nut mechanism will be considered. Therefore, the identified system is actually a typical sandwich system with backlash-like hysteresis. In this section, only the identification procedure of axis A will be presented due to the limited space. The corresponding models used to describe the behavior of axis A are shown as follows:

(1)
the input linear model (L₁):
()
(2)
the model of the backlash-like hysteresis:
()
(3)
the output linear model (L₂):
()

where y(k) is the moving speed of the work platform.

Based on the operating requirement, a sequence of square wave plus sinusoidal wave is used to excite the system within the operating range. The corresponding amplitude of the input varies in the range between −1.09 V and 1.05 V, and the sample period is 0.5 ms.

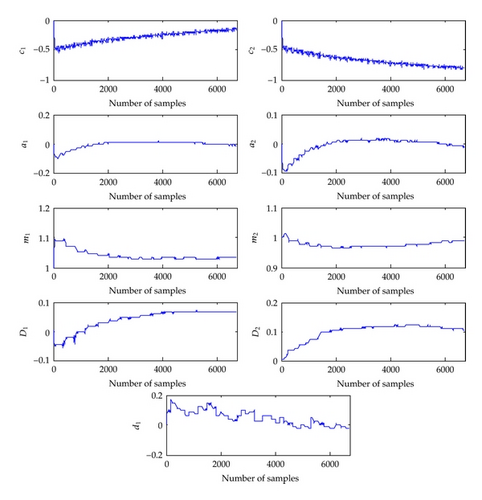
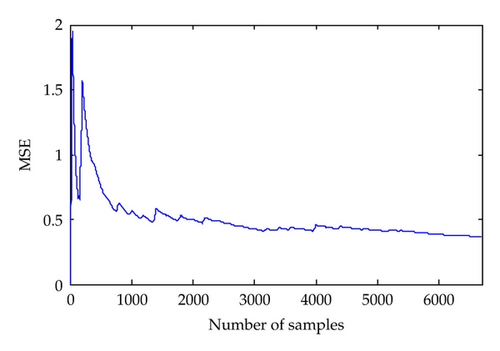
In this model, both b₀ and d₀ are set to one. The initial values of the other parameters are chosen as η(0) = 0.00116, μ = 1, θ₀ = [0, 0, 0, 0, 1, 1, 0.001, 0.001, 0] ^T , and β(k₀) = 0. After 6700 steps, the convergence of the estimation is achieved. Figure 5 illustrates the corresponding procedure of the parameter estimation. It shows that the estimate procedure converges quickly. Figure 6 shows the corresponding mean square error (MSE) of the parameter estimation. We can see that the MSE is decreased sharply in the beginning, at the 180th step, and a local minimum can be found. After that, the algorithm jumps out of the local minimum, and the corresponding MSE gradually converges to a constant of about 0.4.

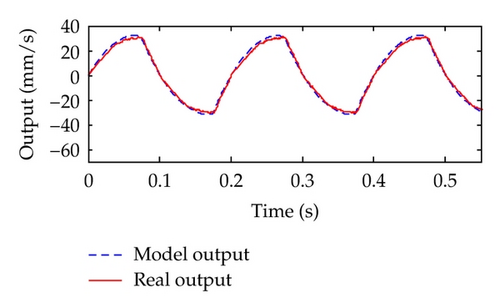
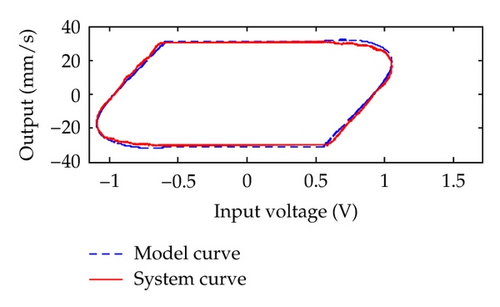
Then, the corresponding model validation result is shown in Figure 7(a), while Figure 7(b) shows the comparison of the input-output plots between the proposed model and the real data. The maximum relative modeling error is less than 11%. Moreover, it is obvious that the obtained model can accurately approximate the behavior of the X-Y moving positioning stage. Hence, it can be concluded that the proposed identification method is rather promising in engineering application.

7. Conclusion

In this paper, a recursive gradient-based identification algorithm for the sandwich system with backlash-like hysteresis is proposed. The subgradient is applied to the search of gradient direction at the nonsmooth points of the system. In order to find the proper search direction at the nonsmooth points, the technique of so-called bundle method is utilized. Simulation results have shown that the proposed algorithm has provided us with an option for identification of nonsmooth dynamic systems, and it provides a novel method to identify the more complicated nonsmooth systems. The experimental results of X-Y stage also show that the proposed method has potential in engineering applications.

Acknowledgments

This work was supported by the projects of Shanghai Normal University (DZL811, DRL904, and DYL201005); the projects of Shanghai Education Commission (11YZ92); the project of NSFC (Grant nos. 60971004 and 61171088); the projects of Science and Technology. Commission of Shanghai (09220503000, 10JC1412200, and 09ZR1423400).

Appendix

Based on (3.5) and Step 3 of the algorithm, it is obtained

()

Subtracting the local optimal value θ₁ from both sides of (A.1), it leads to

()

Rewrite (A.2) as

()

where

Choose the quadratic function as

()

According to (A.3), it leads to

()

, if (3.5) holds, then the cutting-plane model is

()

Based on the definitions of β_j(k) and α_j(k), as well as the idea of bundle method, we know that

. Thus, considering (A.6) yields

()

Choosing θ = θ₁ and holding (A.7) yield

()

Based on (A.5) and (A.8), we obtain

()

According to the idea of the gradient algorithm and [16], we know that

()

Hence, the change of e(k) is written as

()

According to (3.5) and Step 3 of the algorithm, it yields:

()

From (A.11) and (A.12), we get

()

According to (A.10) and (A.13), we obtain

()

Based on (A.4), (A.9), and (A.14), it leads to the following:

()

and

, we have

()

Hence, the parameters θ can be convergent to a local optimal value.

References

1 Bershad N. J., Celka P., and McLaughlin S., Analysis of stochastic gradient identification of Wiener-Hammerstein systems for nonlinearities with Hermite polynomial expansions, IEEE Transactions on Signal Processing. (2001) 49, no. 5, 1060–1071, https://doi.org/10.1109/78.917809.
10.1109/78.917809
Web of Science® Google Scholar
2 Tan A. H. and Godfrey K., Identification of Wiener-Hammerstein models using linear interpolation in the frequency domain (LIFRED), IEEE Transactions on Instrumentation and Measurement. (2002) 51, no. 3, 509–521, https://doi.org/10.1109/TIM.2002.1017722.
10.1109/TIM.2002.1017722
Web of Science® Google Scholar
3 Boutayeb M. and Darouach M., Recursive identification method for MISO Wiener-Hammerstein model, IEEE Transactions on Automatic Control. (1995) 40, no. 2, 287–291, https://doi.org/10.1109/9.341794, 1312896, ZBL0819.93024.
10.1109/9.341794
Web of Science® Google Scholar
4 Cerone V. and Regruto D., Bounding the parameters of linear systems with input backlash-like hysteresis, Proceedings of the American Control Conference, June 2005, Portland, Ore, USA, 4476–4481.
Google Scholar
5 Bai E.-W., Identification of linear systems with hard input nonlinearities of known structure, Automatica. (2002) 38, no. 5, 853–860, https://doi.org/10.1016/S0005%2D1098(01)00281%2D3, 2133360, ZBL1010.93032.
10.1016/S0005-1098(01)00281-3
Web of Science® Google Scholar
6 Giri F., Rochdi Y., Chaoui F. Z., and Brouri A., Identification of Hammerstein systems in presence of hysteresis-backlash and hysteresis-relay nonlinearities, Automatica. (2008) 44, no. 3, 767–775, https://doi.org/10.1016/j.automatica.2007.07.005, 2527074.
10.1016/j.automatica.2007.07.005
Web of Science® Google Scholar
7 Dong R., Tan Y., and Chen H., Recursive identification for dynamic systems with backlash, Asian Journal of Control. (2010) 12, no. 1, 26–38, https://doi.org/10.1002/asjc.157, 2676768.
10.1002/asjc.157
PubMed Web of Science® Google Scholar
8 Dong R., Tan Q., and Tan Y., Recursive identification for dynamic systems with output backlash-like hysteresis and its convergence, International Journal of Applied Mathematics and Computer Science. (2009) 19, no. 4, 631–638.
10.2478/v10006-009-0050-2
Web of Science® Google Scholar
9 Dong R. and Tan R., Online identification algorithm and convergence analysis for sandwich systems with backlash, International Journal of Control, Automation and Systems. (2011) 9, no. 3, 1–7.
10.1007/s12555-011-0320-2
Web of Science® Google Scholar
10 Eitzinger C., Nonsmooth training of fuzzy neural networks, Soft Computing. 8, 443–448.
10.1007/s00500-003-0299-6
Web of Science® Google Scholar
11 Mäkelä M. M., Miettinen M., Lukšan L., and Vlček J., Comparing nonsmooth nonconvex bundle methods in solving hemivariational inequalities, Journal of Global Optimization. (1999) 14, no. 2, 117–135, https://doi.org/10.1023/A:1008282922372, 1694145, ZBL0947.90125.
10.1023/A:1008282922372
Web of Science® Google Scholar
12 Miller S. A., An inexact bundle method for solving large structured linear matrix inequality [Doctoral dissertation], 2001, University of California, Santa Barbara, Calif, USA.
Google Scholar
13 Lemaréchal C., G. L. Nemhauser, A. H. G. Rinnooy Kan, and M. J. Todd, Nondifferentiable optimization, Optimization, 1989, 1, North-Holland, Amsterdam, The Netherland, 529–572, https://doi.org/10.1016/S0927%2D0507(89)01008%2DX, 1105106.
10.1016/S0927-0507(89)01008-X
Google Scholar
14 Goldberg D. E., Genetic Algorithms in Search, Optimization, and Machine Learning, 1998, Addison-Wesley, .Reading, Mass, USA.
Google Scholar
15 Fletcher R., Practical Methods of Optimization, 1987, 2nd edition, John Wiley & Sons, Chichester, 955799.
Google Scholar
16 Ku C.-C. and Lee K. Y., Diagonal recurrent neural networks for dynamic systems control, IEEE Transactions on Neural Networks. (1995) 6, no. 1, 144–156, https://doi.org/10.1109/72.363441.
10.1109/72.363441
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Nonsmooth Recursive Identification of Sandwich Systems with Backlash-Like Hysteresis

Abstract

1. Introduction

2. Brief Description of Sandwich Systems with Backlash

3. The Nonsmooth Estimation of the Sandwich Model with Backlash-Like Hysteresis

4. Convergence of the Estimation

5. Simulation

6. Application to an X-Y Moving Positioning Stage

7. Conclusion

Acknowledgments

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Nonsmooth Recursive Identification of Sandwich Systems with Backlash-Like Hysteresis

Abstract

1. Introduction

2. Brief Description of Sandwich Systems with Backlash

3. The Nonsmooth Estimation of the Sandwich Model with Backlash-Like Hysteresis

4. Convergence of the Estimation

5. Simulation

6. Application to an X-Y Moving Positioning Stage

7. Conclusion

Acknowledgments

Appendix

References

Citing Literature

Figures

References

Related

Information