Journal of Applied Mathematics
Volume 2012, Issue 1 435924
Research Article
Open Access

Energy-Driven Image Interpolation Using Gaussian Process Regression

Lingling Zi, 

Lingling Zi

Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China bupt.edu.cn

School of Electronic and Information Engineering, Liaoning Technical University, Huludao 125105, China lnu.edu.cn

Search for more papers by this author
Junping Du, 

Corresponding Author

Junping Du

Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China bupt.edu.cn

Search for more papers by this author
First published: 08 July 2012
https://doi.org/10.1155/2012/435924
Citations: 2
Academic Editor: Baocang Ding

Abstract

Image interpolation, as a method of obtaining a high-resolution image from the corresponding low-resolution image, is a classical problem in image processing. In this paper, we propose a novel energy-driven interpolation algorithm employing Gaussian process regression. In our algorithm, each interpolated pixel is predicted by a combination of two information sources: first is a statistical model adopted to mine underlying information, and second is an energy computation technique used to acquire information on pixel properties. We further demonstrate that our algorithm can not only achieve image interpolation, but also reduce noise in the original image. Our experiments show that the proposed algorithm can achieve encouraging performance in terms of image visualization and quantitative measures.

1. Introduction

Image interpolation is a very important aspect of image processing and involves the use of a known pixel set to produce an unknown pixel set, resulting in an image of higher resolution [1, 2]. This technique is widely used in remote sensing, aerospace, infrared imaging, low-light level night imagery, and other fields [3–5]. However, maintaining image quality during image interpolation is still a difficult issue [6]. To address this, many image interpolation methods have been proposed. For example, traditional bilinear interpolation computes the unknown pixel value using the location information between the adjacent pixels. This technique does not consider the contents of the image, so edge blurring will occur in the interpolated image [7, 8]. In order to capture image details more clearly, an artifact-free image upscaling method called ICBI [9] has recently been proposed, which uses iterative curvature-based interpolation to obtain a high image quality, but does not take into account underlying local information between image patches. Local image information can be mined according to its structural redundancy characteristic, as proposed by Glasner et al. [10]. This characteristic can lay the foundations for the training and predicting of a statistical model [11, 12]. A statistical model known as Gaussian process regression (GPR) was first applied in the reconstruction of high-resolution images in 2011 and has been shown to be capable of generating an image with sharp edges by extracting the necessary information from a low-resolution image [13]. However, it should be noted that this method only uses the local structural information for each pixel’s neighborhood, so it can still generate unexpected details. To develop the above techniques, we propose here a novel energy-driven interpolation algorithm employing Gaussian process regression (EGPR) (Figure 1). This algorithm not only emphasizes the influence of adjacent pixel properties on interpolated values, but also brings into full play the role of the statistical model.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Overview of our approach for image interpolation.

Our contribution is twofold. Firstly, we propose a framework for both magnification and deblurring in order to fulfill the interpolation task for low-resolution images with low noise. Secondly, we demonstrate an energy-driven approach based on the properties of adjacent pixels within this framework. In addition, we define the processing unit and its properties for better implementation of the EGPR algorithm.

The rest of the paper is structured as follows. Section 2 discusses GPR. Section 3 illustrates the proposed EGPR algorithm. Section 4 presents experimental work carried out to demonstrate the effectiveness of our algorithm. Section 5 concludes the paper.

2. Gaussian Process Regression

In recent years, GPR has become a hot issue in the field of machine learning and has attracted great academic interest [14–16]. It has many advantages, including its rigorous underlying statistical learning theory, easy regression process implementation, few parameters, and improved model interpretability [17–19]. As a result of these benefits, it has been used in many areas [20–23]; however, to the best of our knowledge, it has not yet been fully utilized in image interpolation. Rasmussen and Williams [24] defined the Gaussian process and noted in particular that a Gaussian process is completely specified by its mean and covariance functions ((2.1) and (2.2), resp.):
()
()
where x and x′ are any random variables. In particular, they could represent n-dimensional input or output vectors. The Gaussian process can be written as follows:
()
There are a variety of covariance functions, of which one of the most commonly used is the squared exponential (SE) covariance function
()
In Gaussian processes, the marginal likelihood p(y∣X) at a point is very useful and is the integral of the likelihood multiplied by the prior probability
()
We can rewrite (2.5) as follows:
()
We can make use of Gaussian identities to obtain (2.7), in order to compute the log marginal likelihood. The conjugate gradients method has been applied to solve this equation. Using this approach, we can obtain the hyperparameters of the covariance function. Further details of GPR can be found in [24] as follows:
()

3. The Proposed Algorithm

In this paper, we combine the energy-driven approach with GPR to accomplish the task of image interpolation. The proposed algorithm models low-resolution image data as a function of a probability distribution that satisfies a local static Gaussian process. This algorithm framework is shown in Figure 2 and is broadly divided into the training process and prediction process. Firstly, the GPR model can be established using the low-resolution image data. Next, this model is used to predict the unknown pixel values of a high-resolution image by adopting an energy computation approach. Through the above two steps, we produce a high-quality enlarged image. The process is further clarified by the following:
()
where L and H denote the input low-resolution image with a little noise and the output high-resolution image, respectively, L′   denotes the noise-free low-resolution image, H′ denotes the initial high-resolution image, sdenotes the upsampling factor, and d and f denote the clear transfer function and energy transfer function, respectively.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Architecture of the proposed algorithm.

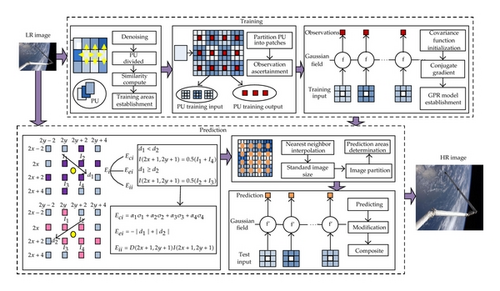
3.1. Training

The following definitions are used in the EGPR algorithm.

Definition 3.1. A given image L is divided into many regions of equal size, and each region is defined as a processing unit (PU). Each PU is also divided into 3 × 3 overlapping image patches (the total number is M). The center of each patch is defined as an output vector YTR of PU, where , while the nearest eight values are defined as an input vector XTR of PU, where

()

Definition 3.2. Given a total of N pixels in each PU, the pixels are sorted and denoted as I1, I2 … IN. Imax  ave, Imin  ave, and Iave are defined using the following formulae:

()
where top represents the number of the largest pixels used and below the number of the smallest pixels used. Then Imax  ave, Imin  ave, and Iave are called basic properties of PU.

To facilitate the operation of the PU, it is necessary to introduce some properties in advance.

Property 1. Given a number N in each PU, if Imax  ave = 0, then pixel value Ii = 0, where i ≤ N.

Property 2. Given xij, if xij = a, then its corresponding output vector value is yij = a, where yij ∈ YTR, i ∈ M, j = 1.

Denoising is the first step in the EGPR algorithm, and we use the following formula (3.4) to obtain noise-free images:
()
where θ and B represent empirical values, and Ineighbor represents the adjacent pixel value.

Before applying GPR, we can obtain the particular relationship between the input and output vectors of PU according to Properties 1 and 2. Pixels with this relationship need not be included in the following GPR training, so the predicted values can be directly obtained, saving time and speeding up the EGPR algorithm.

Training plays an important role in the EGPR algorithm, and we adopt a different approach from that used in [13]. Our algorithm contains two processes: training domain establishment and GPR model foundation. In the first stage, we search possible training domains along the four directions of each specific PU. Next, we compute the structural similarity between directions to determine the definite training domain. Inspired by the concept of image SSIM, we define the PU structural similarity as follows.

Definition 3.3 (PU structural similarity). Given two processing units P and Q, their structural similarity is defined as

()
where C1 and C2 are constants, and the other components are calculated as follows:
()

When the search step count reaches the predefined number, or if the PU structure similarity falls below a certain value, the first stage is complete. In the second stage, we apply a Gaussian process prior probability and establish the GPR model with Gaussian noise γ (see (3.7) below) using the image data from training domains. In (3.7), “GP” denotes a Gaussian process
()

When aiming to achieve high-quality images, the conjugate gradients method is chosen to obtain the model hyperparameters, including mean, variance, and log marginal likelihood. Notice that different iteration numbers in the conjugate gradients method may lead to different prediction accuracies. Figure 3 shows the interpolation images obtained after 50 iterations and 100 iterations, where it can be seen that the latter is better than the former.

Details are in the caption following the image
Figure 3 (a) Iteration = 50
Open in figure viewerPowerPoint
Images obtained after adaptation with different numbers of iterations. In (a), many black points are observed, each indicating a zero prediction for the pixels. In (b), the black points have been eliminated.
Details are in the caption following the image
Figure 3 (b) Iteration = 100
Open in figure viewerPowerPoint
Images obtained after adaptation with different numbers of iterations. In (a), many black points are observed, each indicating a zero prediction for the pixels. In (b), the black points have been eliminated.

3.2. Prediction

Inspired by the ICBI algorithm, we firstly compute the initial pixel value H′(2x + 1,2y + 1) according to the following formulae:
()
()
()
However, the pixel value obtained is only a roughly estimated value and needs further refinement. Following [9], we establish (3.11) to calculate the energy of each interpolated pixel, and the initial estimate can be modified accordingly,
()
where c, e, and i are chosen to adjust the energy contributions from the three parts.
Ec represents the curvature continuity energy and can be computed with the following formulae:
()
where αi(i = 1 … 4) are weight values (see (3.13)), and d1 and d2 have the same meanings as above. θ is set as the threshold
()
The second energy term Eb represents the curvature enhancement energy and can be computed by
()
The third energy term, Ei, represents the isolevel curves smoothing energy and can be computed with
()
where D(2x + 1,2y + 1) can be computed as follows:
()

Suppose that the low-resolution image Lij is of size m × n and that it is changed to the corresponding interpolated image of size ((m × 2scale) − (2scale − 1)) × ((n × 2scale) − (2scale −  1)), where “scale” denotes the magnification factor. Then we use the nearest interpolation algorithm for the missing pixels in order to obtain the image of size (m  ×  2scale) × (n  ×  2scale).

Similarly, we partition into overlapping processing units. The eight adjacent pixels of each pixel are treated as GPR model test input data based on the model M which was obtained from the training process. Note that if PU has Property 1 or Property 2, then we can directly obtain the corresponding pixel values. Otherwise, we capture the prediction distribution of unknown pixels in the initial high-resolution image. The joint distribution of the training domain output y and the test output f’ is given by the following equation:
()
where X denotes the GPR training data matrix, X′ is the test matrix, and COV(X, X′) is the n × n matrix of covariances. Therefore, we can derive the predictive distribution based on the obtained model M:
()

During the prediction of high-resolution image pixels, two rules should be obeyed. Firstly, the PU divided by the initial high-resolution image should correspond to that divided by the low-resolution image. Secondly, the gradient algorithm should satisfy the common positive definite matrix. If not, it will lead to a zero prediction, and the prediction value will need modifying. The modification method can be utilized to maintain the original interpolated pixel value. Finally, we combine all the processing units together in a smooth manner to obtain the high-resolution images without noise.

4. Experimental Results and Discussion

In this section, we compare the experimental results obtained using the proposed algorithm with those obtained using the bilinear algorithm, GPR algorithm [13], and ICBI algorithm [9]. Each algorithm was run in MATLAB. In order to evaluate algorithm performance, we first downsampled original high-quality images to acquire low-resolution images. Then we enlarged these low-resolution images by utilizing the different interpolation algorithms and compared the enlarged images with the original high-quality images. In all experiments, we set the PU size to 30 × 30, but this may be increased according to the magnification factor. At the same time, we used zero mean and square exponential functions as the respective mean and covariance functions in the EGPR. The covariance function required two hyperparameters: a characteristic length scale, the default value of which was 0.21, and the standard deviation of the signal, the default value of which was 0.08. In addition, to achieve color image interpolation, we trained and predicted the GPR model separately for each of the R, G, and B channels.

Figure 4 shows the interpolation results from the four algorithms when “scale” was set as 1. Figures 4(a)–4(d) are comparisons of image 1, and Figures 4(e)–4(h) are comparisons of image 2. In the enlarged red-bordered region, it can be seen that the bilinear method introduces jaggy effects, the GPR method reduces these jaggy effects, and the ICBI method achieves a clear edge but is still a little blurry. By employing the energy computation based on properties of adjacent pixels, our new method generates a clearer image without noise.

Details are in the caption following the image
Figure 4 (a) Bilinear
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (b) GPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (c) ICBI
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (d) EGPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (e) Bilinear
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (f) GPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (g) ICBI
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.
Details are in the caption following the image
Figure 4 (h) EGPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 1. Parts (a)–(d) show image 1. Parts (e)–(h) show image 2.

Similarly, Figures 5 and 6 demonstrate the interpolation results with scales of 2 and 3, respectively. From these figures, it can be seen that our method achieved the clearest and smoothest enlarged image of the four methods tested, for example, along edges on the root hand in Figure 6(h). Moreover, the advantages of our proposed algorithm become more enhanced at greater enlargement factors.

Details are in the caption following the image
Figure 5 (a) Bilinear
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (b) GPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (c) ICBI
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (d) EGPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (e) Bilinear
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (f) GPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (g) ICBI
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 5 (h) EGPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 2. Parts (a)–(d) show image 3. Parts (e)–(h) show image 4.
Details are in the caption following the image
Figure 6 (a) Bilinear
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (b) GPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (c) ICBI
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (d) EGPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (e) Bilinear
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (f) GPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (g) ICBI
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.
Details are in the caption following the image
Figure 6 (h) EGPR
Open in figure viewerPowerPoint
Comparison of images obtained using four methods, with scale = 3. Parts (a)–(d) show image 5. Parts (e)–(h) show image 6.

To further validate our algorithm, we also provide objective measurements. Peak signal-to-noise ratio (PSNR) and root mean square (RMS) error are traditional quantitative measures of accuracy, and by comparing their values for the above images, we can conclude that the proposed EGPR algorithm yields interpolated pixel values that are much closer to their original high-quality values than those obtained with the bilinear algorithm, GPR algorithm, and ICBI algorithm. Tables 1 and 2 summarize the PSNR and RMS values for each algorithm at different magnification factors and for each image. It can be observed that the PSNR values for images obtained using the EGPR algorithm are the highest, and those using the bilinear algorithm are the lowest. Further, RMS values for images obtained using the EGPR algorithm are the lowest, and those using the bilinear algorithm are the highest. Overall, it can be clearly demonstrated that our new method outperforms the other three algorithms.

Table 1. Comparison of PSNR for the four interpolation methods when applied to test images.
Image Scale Bilinear GPR ICBI EGPR
Image 1 1 32.9940 33.2792 33.3456 33.3986
Image 2 1 30.6314 30.7861 31.3684 31.4594
Image 3 2 29.5738 29.4194 29.7173 29.7213
Image 4 2 27.7717 27.4767 27.8485 27.8625
Image 5 3 23.4038 24.4366 24.7153 24.7171
Image 6 3 24.3122 25.1477 25.6880 25.6909
Table 2. Comparison of RMS for the four interpolation methods when applied to test images.
Image Scale Bilinear GPR ICBI EGPR
Image 1 1 16.4437 15.8419 15.7032 15.6004
Image 2 1 21.1046 20.3410 19.1890 18.9614
Image 3 2 24.9225 24.8861 24.4329 24.4191
Image 4 2 31.0516 32.1427 30.6882 30.6118
Image 5 3 50.8161 44.8762 43.3017 43.2633
Image 6 3 45.9833 41.5720 39.0571 39.0412

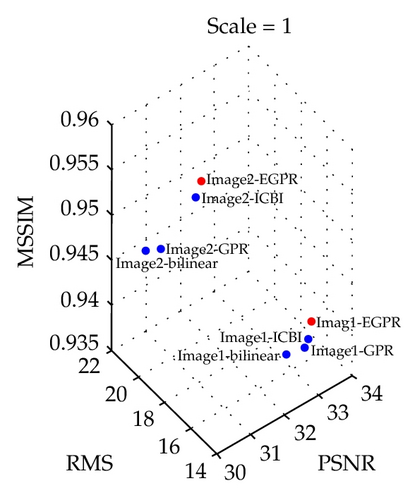
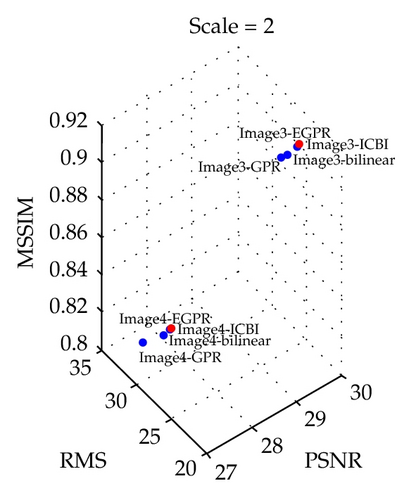
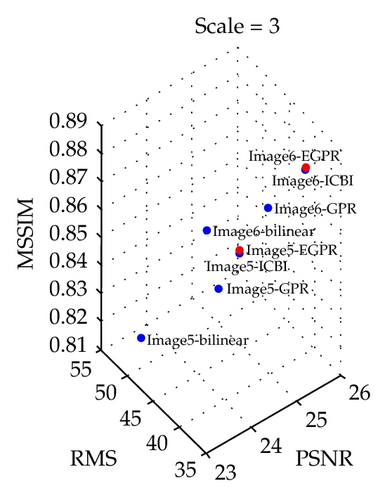
MSSIM [25] is an image quality assessment index which assesses the image visibility quality from an image formation point of view under the assumption of the correlation between human visual perception and image structural information. We compared the MSSIM obtained using the EGPR algorithm at different scale values with the corresponding values obtained using the bilinear, GPR, and ICBI algorithms, as shown in Table 3. It is noted that our new algorithm achieves a greater MSSIM than the other three algorithms, and the results show that the images obtained using our algorithm are closer to the original high-resolution images in terms of image structure similarity.

Table 3. Comparison of MSSIM for the four interpolation methods when applied to test images.
Image Scale Bilinear GPR ICBI EGPR
Image 1 1 0.936 0.937 0.938 0.940
Image 2 1 0.946 0.947 0.953 0.955
Image 3 2 0.905 0.906 0.909 0.910
Image 4 2 0.812 0.808 0.815 0.816
Image 5 3 0.818 0.837 0.850 0.851
Image 6 3 0.857 0.865 0.878 0.879

In addition, Figure 7 clearly demonstrates the quantitative assessment results for each image at different magnification levels. In this figure, the blue dots represent the quality scores of the images obtained using the comparison algorithms, and the red dots represent those obtained using our algorithm. Our interpolation algorithm is notably superior to the other algorithms, according to all three objective measurements. The proposed algorithm therefore yielded encouraging performance in terms of image visualization and quantitative quality assessment, making it a competitive image interpolation algorithm.

Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
Quantitative quality assessment results for the four interpolation methods.
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
Quantitative quality assessment results for the four interpolation methods.
Details are in the caption following the image
Figure 7 (c)
Open in figure viewerPowerPoint
Quantitative quality assessment results for the four interpolation methods.

5. Conclusions

In this paper, we have presented a novel EGPR method for image interpolation. The main feature of this new algorithm is its ability to obtain relatively high prediction accuracy of the unknown pixels by fully utilizing underlying image patch information. The implementation process involves two steps: training and prediction. The former creates a GPR model using only single-image data as the training set, and the latter combines energy computation with the acquired model to produce a high-resolution image. Experiments have shown that our algorithm can yield encouraging performance not only in terms of image visualization but also in terms of PSNR, RMS, and MSSIM quality measures. However, better image interpolation comes at the expense of greater algorithm complexity. Methods of improving the algorithm efficiency need further investigation. In future, we can improve this algorithm to address the problem of the interpolation of image sequences. Images in the same sequence are also subject to the recurrence phenomenon, whereby images contain spatial-temporal correlation [26]. We believe that this problem can be addressed using the improved EGPR algorithm by finding an appropriate energy-driven computation and training mode.

Acknowledgments

This work was supported by the National Basic Research Program of China (973 Program) 2012CB821200 (2012CB821206), the National Natural Science Foundation of China (no. 91024001, no. 61070142), and the Beijing Natural Science Foundation (no. 4111002).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.