Convergence Theorems for Equilibrium Problems and Fixed-Point Problems of an Infinite Family of k_i-Strictly Pseudocontractive Mapping in Hilbert Spaces

Let F be a bifunction from C × C into R satisfying (A1), (A2), (A3), and (A4). Then, for any r > 0 and x ∈ H, there exists z ∈ C such that

Furthermore, if T_rx = {z ∈ C : F(z, y) + (1/r)(y − z, z − x) ≥ 0, ∀y ∈ C}, then the following hold:

• (1)

  T_r is single-valued.

• (2)

  T_r is firmly nonexpansive, that is,

  $$ (2.5)

• (3)

  F(T_r) = EP (F).

• (4)

  EP (F) is closed and convex.

Let S : C → H be a k-strictly pseudo-contractive mapping. Define T : C → H by Tx = λx + (1 − λ)Sx for each x ∈ C. Then, as λ ∈ [k, 1), T is nonexpansive mapping such that F(T) = F(S).

In a Hilbert space H, there holds the inequality

Lemma 2.4 (see [25].)Let H be a Hilbert space and C be a closed convex subset of H, and T : C → C a nonexpansive mapping with F(T) ≠ ∅. If {x_n} is a sequence in C weakly converging to x and if {(I − T)x_n} converges strongly to y, then (I − T)x = y.

Lemma 2.5 (see [26].)Let {x_n} and {z_n} be bounded sequences in a Banach space E and {γ_n} be a sequence in [0,1] satisfying the following condition

Suppose that x_n+1 = γ_nx_n + (1 − γ_n)z_n, n ≥ 0 and lim  _n→∞sup (∥z_n+1 − z_n∥ − ∥x_n+1 − x_n∥) ≤ 0. Then lim  _n→∞∥z_n − x_n∥ = 0.

Lemma 2.6 (see [27].)Assume that {a_n} is a sequence of nonnegative real numbers such that

where {b_n} is a sequence in (0,1) and {δ_n} is a sequence in R, such that

• (i)

  $$.

• (ii)

  lim _n→∞ sup δ_n ≤ 0 or $$.

Then, lim  _n→∞ a_n = 0.

Remark 2.7. If k_i = 0, and σ_i = 0 for i ∈ N, then the definition of W_n in (2.9) reduces to the definition of W_n in (1.13).

Lemma 2.8 (see [18].)Let C be a nonempty closed convex subset of a strictly convex Banach space. Let $$ be an infinite family of nonexpansive mappings of C into itself and let {τ_i} be a real sequence such that 0 < τ_i ≤ b < 1 for every i ∈ N. Then, for every x ∈ C and k ∈ N, the limit lim  _n→∞ U_n,kx exists.

Lemma 2.9 (see [18].)Let C be a nonempty closed convex subset of a strictly convex Banach space. Let $$ be an infinite family of nonexpansive mappings of C into itself such that $$ and let {τ_i} be a real sequence such that 0 < τ_i ≤ b < 1 for every i ∈ N. Then, $$.

Lemma 2.10. Let C be a nonempty closed convex subset of a strictly convex Banach space. Let {S_i} be an infinite family of k_i-strictly pseudo-contractive mappings of C into itself such that $$. Define $$ and σ_i ∈ [k_i, 1) and let {τ_i} be a real sequence such that 0 < τ_i ≤ b < 1 for every i ∈ N. Then, $$.

Lemma 2.11 (see [28].)Let C be a nonempty closed convex subset of a Hilbert space. Let $$ be an infinite family of nonexpansive mappings of C into itself such that $$ and let {τ_i} be a real sequence such that 0 < τ_i ≤ b < 1 for every i ∈ N. If K is any bounded subset of C, then

Theorem 3.1. Let C be a nonempty closed convex subset of a real Hilbert space H and F be a bifunction from C × C → R satisfying (A1)–(A4). Let S_i : C → C be a k_i-strictly pseudo-contractive mapping with $$ and {τ_i} be a real sequence such that 0 < τ_i ≤ b < 1, i ∈ N. Let f be a contraction of H into itself with β ∈ (0,1) and B be k-Lipschitzian and η-strongly monotone operator on H with coefficients k, η > 0, 0 < μ < 2η/k², 0 < r < (1/2)μ(2η − μk²)/β = (τ/β) and τ < 1. Let {x_n} be a sequence generated by

where $$ and {W_n : C → C} is the sequence defined by (2.9). If {α_n}, {β_n}, {δ_n}, and {λ_n} satisfy the following conditions:

• (i)

  {α_n}⊂(0,1), lim _n→∞ α_n = 0,   $$,

• (ii)

  0 < lim _n→∞inf β_n ≤ lim _n→∞sup β_n < 1,

• (iii)

  0 < lim _n→∞inf δ_n ≤ lim _n→∞sup δ_n < 1, lim _n→∞ | δ_n+1 − δ_n | = 0,

• (iv)

  {λ_n}⊂(0, ∞), lim _n→∞ λ_n > 0, lim _n→∞ | λ_n+1 − λ_n | = 0.

Then {x_n} converges strongly to $$, where z is the unique solution of variational inequality

that is, z = P_F(W)∩EP(F)(I − μB + rf)z, which is the optimality condition for the minimization problem where h is a potential function for rf (i.e., h^′(z) = rf(z) for z ∈ H).

Proof . We divide the proof into five steps.

Step 1. We prove that {x_n} is bounded.

Noting the conditions (i) and (ii), we may assume, without loss of generality, that α_n/(1 − β_n) ≤ min {1,1/τ}. For x, y ∈ C, we obtain

Take $$. Since $$ and $$, then from Lemma 2.1, we know that, for any n ∈ N, Furthermore, since W_np = p and (3.6), we have Thus, it follows from (3.7) that By induction, we have Hence, {x_n} is bounded and we also obtain that {u_n}, {W_nu_n}, {y_n}, {By_n}, and {f(x_n)} are all bounded. Without loss of generality, we can assume that there exists a bounded set K ⊂ C such that {u_n}, {W_nu_n}, {y_n}, {By_n}, {f(x_n)} ∈ K, for all  n ∈ N.

Step 2. We show that lim _n→∞∥x_n − x_n+1∥ = 0.

Let x_n+1 = (1 − β_n)z_n + β_nx_n. We note that

and then Therefore, It follows from (3.2) that

We will estimate ∥u_n+1 − u_n∥. From $$ and $$, we obtain

Taking y = u_n in (3.14) and y = u_n+1 in (3.15), we have

So, from (A2), one has

furthermore, Since lim _n→∞λ_n > 0, we assume that there exists a real number such that λ_n > a > 0 for all n ∈ N. Thus, we obtain which means where L₁ = sup {∥u_n+1 − x_n+1∥ : n ∈ N}.

Next, we estimate ∥W_n+1u_n+1 − W_nu_n∥. Notice that

From (2.9), we obtain where L₂ ≥ 0 is a constant such that ∥U_n+1,n+1u_n − U_n,n+1u_n∥ ≤ L₂, for all n ∈ N.

Substituting (3.20) and (3.22) into (3.21), we obtain

Hence, we have where L₃ = sup {∥u_n∥ + ∥W_nu_n∥ : n ∈ N}.

Furthermore,

It follows from (3.25) that By the conditions (i), (iii), and (iv), we obtain Hence, by Lemma 2.5, one has which implies Step 3. We claim that lim _n→∞∥Wu_n − u_n∥ = 0.

Notice that

It follows from (3.2) that By the condition (iii), we obtain

First, we show lim _n→∞∥x_n − u_n∥ = 0. From (3.2), for all $$, applying Lemma 2.3 and noting that ∥·∥ is convex, we obtain

Since $$, $$, we have which implies Substituting (3.35) into (3.33), we have which means Noticing lim _n→∞α_n = 0 and lim _n→∞inf (1 − β_n) > 0, we have

Second, we show lim _n→∞∥y_n − x_n∥ = 0. It follows from (3.2) that

This implies that Noticing lim _n→∞ α_n = 0, lim _n→∞inf (1 − β_n) > 0 and (3.30), we have Thus, substituting (3.41) and (3.38) into (3.32), we obtain Furthermore, (3.42), (3.30), and Lemma 2.11 lead to

Step 4. Letting z = P_{F(W)∩EP (F)}(I − μB + rf)z, we show

We know that P_{F(W)∩EP (F)}(I − μB + rf) is a contraction. Indeed, for any x, y ∈ H, we have and hence P_{F(W)∩EP (F)}(I − μB + rf) is a contraction due to (1 − τ + rβ)∈(0,1). Thus, Banach’s Contraction Mapping Principle guarantees that P_{F(W)∩EP (F)}(I − μB + rf) has a unique fixed point, which implies z = P_{F(W)∩EP (F)}(I − μB + rf)z.

Since $$ is bounded in C, without loss of generality, we can assume that $$, it follows from (3.43) that $$. Since C is closed and convex, C is weakly closed. Thus we have ω ∈ C.

Let us show ω ∈ F(W). For the sake of contradiction, suppose that ω ∉ F(W), that is, Wω ≠ ω. Since $$, by the Opial condition, we have

It follows (3.43) that This is a contradiction, which shows that ω ∈ F(W).

Next, we prove that ω ∈ EP (F). By (3.2), we obtain

It follows from (A2) that Replacing n by n_i, we have Since $$ and $$, it follows from (A4) that F(y, ω) ≥ 0 for all y ∈ C. Put z_t = ty + (1 − t)ω for all t ∈ (0,1] and y ∈ C. Then, we have z_t ∈ C and then F(z_t, ω) ≥ 0. Hence, from (A1) and (A4), we have which means F(z_t, y) ≥ 0. From (A3), we obtain F(ω, y) ≥ 0 for y ∈ C and then ω ∈ EP (F). Therefore, ω ∈ F(W)∩EP (F).

Since z = P_{F(W)∩EP (F)}(I − μB + rf)z, it follows from (3.38), (3.42), and Lemma 2.11 that

Step 5. Finally we prove that x_n → ω as n → ∞. In fact, from (3.2) and (3.7), we obtain

which implies From condition (i) and (3.7), we know that $$ and lim _i→∞sup (2/(1 + α_n(τ − rβ))(τ − rβ))〈rf(ω) − μBω, x_n+1 − ω〉≤0. we can conclude from Lemma 2.6 that x_n → ω as n → ∞. This completes the proof of Theorem 3.1.

Remark 3.2. If r = 1, μ = 1, B = I and δ_i = 0, k_i = 0, σ_i = 0 for i ∈ N, then Theorem 3.1 reduces to Theorem 3.5 of Yao et al. [19]. Furthermore, we extend the corresponding results of Yao et al. [19] from one infinite family of nonexpansive mapping to an infinite family of strictly pseudo-contractive mappings.

Remark 3.3. If μ = 1 and δ_i = 0, k_i = 0, σ_i = 0 for i ∈ N, then Theorem 3.1 reduces to Theorem 10 of Colao and Marino [20]. Furthermore, we extend the corresponding results of Colao and Marino [20] from one infinite family of nonexpansive mapping to an infinite family of strictly pseudo-contractive mappings, and from a strongly positive bounded linear operator A to a k-Lipschitzian and η-strongly monotone operator B.

Theorem 3.4. Let C be a nonempty closed convex subset of a real Hilbert space H and F be a bifunction from C × C → R satisfying (A1)–(A4). Let S : C → C be a nonexpansive mapping with F(S)∩EP ≠ ∅. Let f be a contraction of H into itself with β ∈ (0,1) and B be k-Lipschitzian and η-strongly monotone operator on H with coefficients k, η > 0, 0 < μ < 2η/k², 0 < r < (1/2)μ(2η − μk²)/β = τ/β and τ < 1. Let {x_n} be sequence generated by

where $$. If {α_n}, {β_n}, {δ_n}, and {λ_n} satisfy the following conditions:

• (i)

  {α_n}⊂(0,1), lim _n→∞ α_n = 0,   $$,

• (ii)

  0 < lim _n→∞inf β_n ≤ lim _n→∞sup β_n < 1,

• (iii)

  0 < lim _n→∞inf δ_n ≤ lim _n→∞sup δ_n < 1, lim _n→∞ | δ_n+1 − δ_n | = 0,

• (iv)

  {λ_n}⊂(0, ∞), lim _n→∞ λ_n > 0, lim _n→∞ | λ_n+1 − λ_n | = 0.

Then {x_n} converges strongly to z ∈ F(S)∩EP ≠ ∅, where z is the unique solution of variational inequality

that is, z = P_F(S)∩EP(F)(I − μB + rf)z.

Proof . By Theorem 3.1, letting k_i = 0, σ_i = 0, τ_i = 1 and S_i = S for i ∈ N, we can obtain Theorem 3.4.

Example 4.1. Let H = R, C = [−1,1],   S_n = I, τ_n = τ ∈ (0,1),  λ_n = 1, n ∈ N, F(x, y) = 0, for all x, y ∈ C, B = I, r = μ = 1, f(x) = (1/10)x, for all x, with contraction coefficient β = 1/5, δ_n = 1/2, α_n = 1/n, β_n = 1/4 + 1/2n for every n ∈ N. Then {x_n} is the sequence generated by

and {x_n} → 0, as n → ∞, where 0 is the unique solution of the minimization problem

Proof. We divide the proof into four steps.

Step 1. We show

where

Since F(x, y) = 0, for all x, y ∈ C, due to the definition of $$, for all x ∈ H, by Lemma 2.1, we obtain

By the property of P_C, for x ∈ C, we have $$. Furthermore, it follows from (3) in Lemma 2.1 that

Step 2. We show that

It follows from (2.9) that

Furthermore, we obtain Since $$, τ_i = τ for i ∈ N, one has

Step 3. We show that

{x_n} → 0, as n → ∞, where 0 is the unique solution of the minimization problem

In fact, we can see that B = I is k-Lipschitzian and η-strongly monotone operator on H with coefficient k = 1, η = 3/4 such that 0 < μ < 2η/k², 0 < r < (1/2)μ(2η − μk²)/β = τ/β, so we take r = μ = 1. Since $$, n ∈ N, we have

Furthermore, we obtain

Next, we need prove {x_n} → 0, as n → ∞. Since y_n = u_n for all n ∈ N, we have

for all n ∈ N.

Thus, we obtain a special sequence {x_n} of (3.2) in Theorem 3.1 as follows

By Lemma 2.6, it is obviously that x_n → 0, 0 is the unique solution of the minimization problem where c is a constant number.

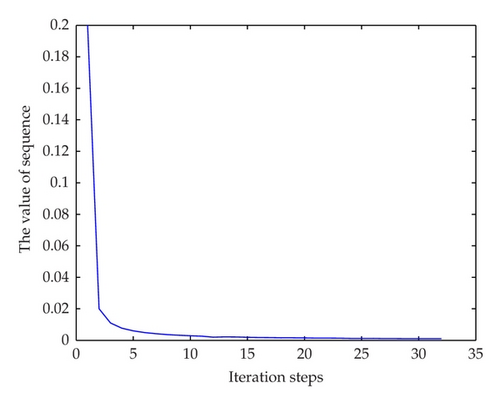
Step 4. Finally, we use software Matlab 7.0 to give the numerical experiment results and then obtain Table 1 which show that the iteration process of the sequence {x_n} is a monotonedecreasing sequence and converges to 0. From Table 1 and the corresponding graph Figure 1, we show that the more the iteration steps are, the more slowly the sequence {x_n} converges to 0.