A New Positive Definite Expanded Mixed Finite Element Method for Parabolic Integrodifferential Equations
Abstract
A new positive definite expanded mixed finite element method is proposed for parabolic partial integrodifferential equations. Compared to expanded mixed scheme, the new expanded mixed element system is symmetric positive definite and both the gradient equation and the flux equation are separated from its scalar unknown equation. The existence and uniqueness for semidiscrete scheme are proved and error estimates are derived for both semidiscrete and fully discrete schemes. Finally, some numerical results are provided to confirm our theoretical analysis.
1. Introduction
Parabolic integrodifferential equations are a class of very important evolution equations which describe many physical phenomena such as heat conduction in material with memory, compression of viscoelastic media, and nuclear reactor dynamics. In recent years, a lot of researchers have studied the numerical methods for parabolic integrodifferential equations, such as finite element methods [1–5], mixed finite element methods [6–9], and finite volume element method [10] and so forth.
In 1994, Chen [11, 12] proposed a new mixed method, which is called a expanded mixed finite element method and proved some mathematical theories for second-order linear elliptic equation. Compared to standard mixed element methods, the expanded mixed method is expanded in the sense that three variables are explicitly approximated, namely, the scalar unknown, its gradient, and its flux (the tensor coefficient times the gradient). In 1997, Arbogast et al. [13] derived and exploited a connection between the expanded mixed method and a certain cell-centered finite difference method. And Chen proved some mathematical theories for second-order quasilinear elliptic equation [14] and fourth-order elliptic problems [15]. With the development of the expanded mixed finite element method, the method was applied to many evolution equations. In [16], some error estimates of the expanded mixed element for a kind of parabolic equation were given. Woodward and Dawson [17] studied the expanded mixed finite element method for nonlinear parabolic equation. Wu and Chen et al. [18–22] studied the two-grid methods for expanded mixed finite-element solution of semilinear reaction-diffusion equations. Song and Yuan [23] proposed the expanded upwind-mixed multistep method for the miscible displacement problem in three dimensions. Guo and Chen [24] developed and analysed an expanded characteristic-mixed finite element method for a convection-dominated transport problem. In 2010, Chen and Wang [25] proposed an H1-Galerkin expanded mixed method for a nonlinear parabolic equation in porous medium flow, and Liu and Li [26] studied the H1-Galerkin expanded mixed method for pseudo-hyperbolic equation. Liu [27], studied the H1-Galerkin expanded mixed method for RLW-Burgers equation and proved semidiscrete and fully discrete optimal error estimates. Jiang and Li [28] studied an expanded mixed semidiscrete scheme for the problem of purely longitudinal motion of a homogeneous bar. In [29, 30], the expanded mixed covolume method was studied for the linear integrodifferential equation of parabolic type and elliptic problems, respectively. In [31], a posteriori error estimator for expanded mixed hybrid methods was studied and analysed.
In 2001, Yang [32] proposed a new mixed finite element method called the splitting positive definite mixed finite element procedure to treat the pressure equation of parabolic type in a nonlinear parabolic system describing a model for compressible flow displacement in a porous medium. Compared to standard mixed methods whose numerical solutions have been quite difficult because of losing positive definite properties, the proposed one does not lead to some saddle point problems. From then on, the method was applied to the hyperbolic equations [33] and pseudo-hyperbolic equations [34].
In this paper, our purpose is to propose and analyse a new expanded mixed method based on the positive definite system [32–34] for parabolic integrodifferential equations. Compared to expanded mixed methods, the proposed mixed element system is symmetric positive definite and avoids some saddle point problems. What is more, both the gradient equation and the flux equation are separated from its scalar unknown equation. The existence and uniqueness for semidiscrete scheme are proved and error estimates are derived for both semidiscrete and fully discrete schemes.
The layout of the paper is as follows. In Section 2, the positive definite expanded mixed weak formulation and semidiscrete mixed scheme are formulated, and the proof of the existence and uniqueness of the discrete solutions is given. Error estimates are derived for both semidiscrete and fully discrete schemes for problems, respectively, in Sections 3 and 4. In Section 5, some numerical results are provided to illustrate the efficiency of our method. Finally in Section 6, we will give some concluding remarks about the positive definite expanded mixed finite element method.
Throughout this paper, C will denote a generic positive constant which does not depend on the spatial mesh parameters hu, hσ and time-discretization parameter δ and may be different at their occurrences. Usual definitions, notations, and norms of the Sobolev spaces as in [35–37] are used. We denote the natural inner product in L2(Ω) or [L2(Ω)] d by (·, ·) with norm or and introduce the function space W = H(div ; Ω) = {ω ∈ [L2(Ω)] d; ∇·ω ∈ L2(Ω)}.
2. A New Expanded Mixed Variational Formulation
Let and be two families of quasi-regular partitions of the domain Ω, which may be the same one or not, such that the elements in the partitions have the diameters bounded by hu and hσ, respectively. Let and be finite element spaces defined on the partitions and .
Remark 2.1. Compared to expanded mixed weak formulation (2.3), the new expanded mixed element system (2.6) is symmetric positive definite, that is to say the gradient function and the flux function system (2.6)(a,b) is symmetric positive definite. And both the gradient equation and the flux equation are separated from its scalar unknown equation (2.6)(c).
Theorem 2.2. There exists a unique discrete solution to the system (2.6).
Proof. Let and be bases of and , respectively. Then, we have the following expressions:
3. Semidiscrete Error Estimates
Lemma 3.1. Assume that the solution of system (2.5) has the regular properties that ut ∈ L2(Hk+1(Ω)), λt, λtt, σt ∈ L2(Hr+1(Ω)), then one has the following estimates:
Let
Theorem 3.2. Assume that the approximate properties (3.1) hold, and the solution of system (2.5) has regular properties that ut, utt ∈ L2(Hk+1(Ω)), λt, λtt, σt, σtt ∈ L2(Hr+1(Ω)). Then one has the error estimates
Proof . Choose wh = θ in (3.6)(a) and zh = −ξt in (3.6)(b), and add the two equations to obtain
Choose zh = θ in (3.6)(b) to get
Differentiating (3.6)(b) and taking zh = ξt, we obtain
4. Fully Discrete Error Estimates
Lemma 4.1. Assume that the solution of system (2.5) has regular properties that ut ∈ L2(Hk+1(Ω)),λt, σt ∈ L2(Hr+1(Ω)). Then one has the estimates
Theorem 4.2. Assume that ∂2u/∂t2, ∂u/∂t ∈ L2(Hk+1(Ω)),∂λ/∂t, ∂2λ/∂t2, ∂σ/∂t, ∂2σ/∂t2 ∈ L2(Hr+1(Ω)), u ∈ L∞(Hk+1(Ω)), and λ, σ ∈ L∞(Hr+1(Ω)), then there exists a constant C such that
Proof . Set wh = θn in (4.7)(a) and zh = −∂tξn in (4.7)(b) and add the two equations to obtain
Note that
By (4.7)(b), we obtain
5. Numerical Example
Dividing the domain Ω into the triangulations of mesh size hu = hσ = h uniformly, considering the piecewise constant space with index k = 0 for the scalar unknown function u and the lowest-order Raviart-Thomas triangular space [42, 45] for the gradient λ and the flux σ and using the backward Euler procedure with uniform time step length δ = 1/M, we obtain some convergence results for , , and with in Table 1. With time t = 1, , the exact solution u, λ, σ is shown in Figures 1, 3, and 5, respectively, and the corresponding numerical solution uh, λh, σh is shown in Figures 2, 4, and 6, respectively.
| (h, δ) | Order | Order | ||
|---|---|---|---|---|
| 1.4527e − 002 | 1.3532e − 001 | |||
| 6.5250e − 003 | 1.15 | 6.9202e − 002 | ||
| 3.0841e − 003 | 1.08 | 3.5363e − 002 | ||
| (h, δ) | Order | |||
| 3.3512e − 001 | 3.8892e − 001 | |||
| 1.6734e − 001 | 1.00 | 1.7291e − 001 | ||
| 8.3746e − 002 | 1.00 | 8.4431e − 002 | ||
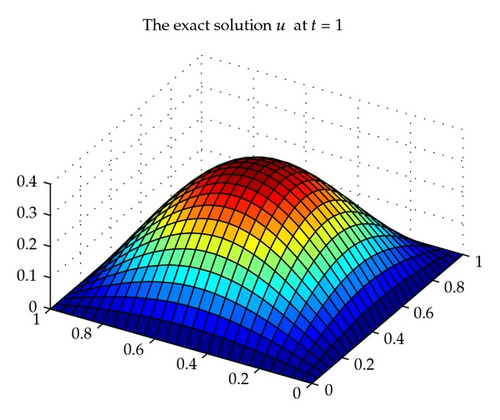
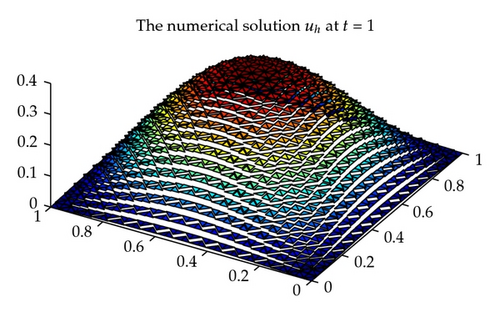
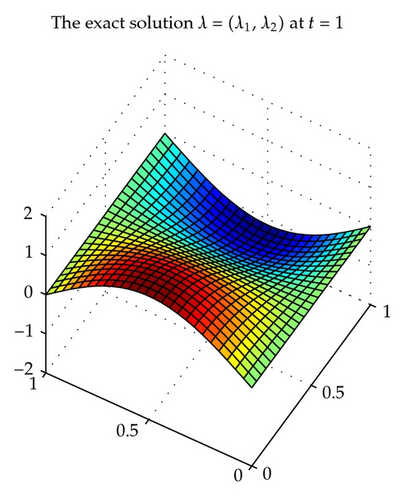
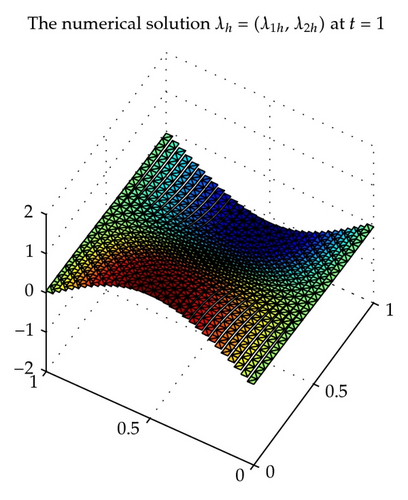
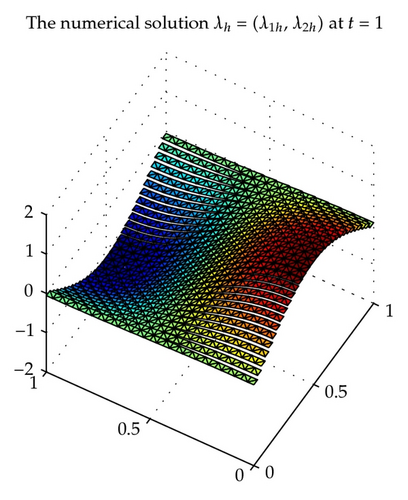
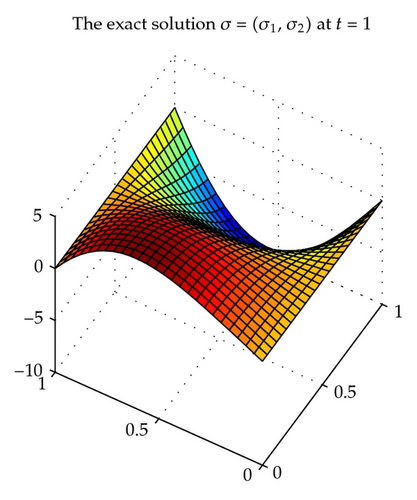
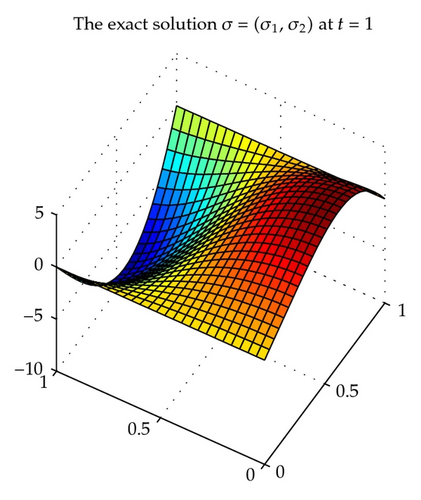
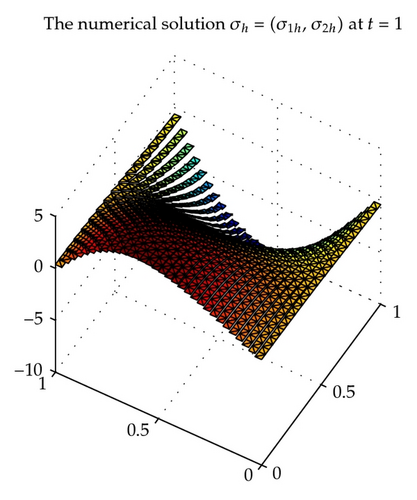
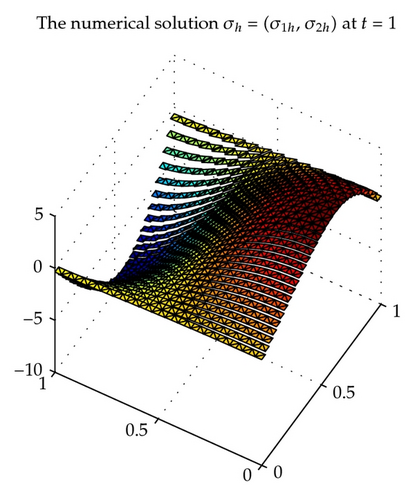
We can see from Table 1 that the convergence rate is order 1 which confirms the theoretical results of Theorem 4.2 for the above chosen spaces and . The numerical results in Table 1 and Figures 1–6 show that new positive definite expanded mixed scheme is efficient.
6. Concluding Remarks
In the paper, a new expanded mixed finite element method based on a positive definite system is proposed for parabolic partial integrodifferential equation. Compared to expanded mixed method and standard mixed methods, the new expanded mixed element system is symmetric positive definite and both the gradient equation and the flux equation are separated from its scalar unknown equation. The existence and uniqueness for semidiscrete scheme are proved and error estimates are derived for both semidiscrete and fully discrete schemes. Finally, some numerical results are provided to confirm our theoretical analysis. In the near further, we will study the others evolution equations such as hyperbolic wave equation, and miscible displacement of compressible flow in porous media.
Acknowledgments
The authors would like to thank the Editor and the referees for their valuable suggestions and comments. This work is supported by the National Natural Science Fund of China (no. 11061021), the Scientific Research Projection of Higher Schools of Inner Mongolia (no. NJ10006, no. NJ10016, no. NJZZ12011), the Program of Higher-level talents of Inner Mongolia University (SPH-IMU, no. Z200901004, no. 125119), and the YSF of Inner Mongolia University (no. ND0702).




