Considering both effects of the s-wave scattering and the atom-atom interaction rather than only the effect of the s-wave scattering, we establish a nonlinear Schrödinger model for many-particle quantum systems and we prove the global existence of a solution to the model and obtain the expression of the solution. Furthermore, we show that the Hamilton energy and the total particle number both are conservative quantities.

1. Introduction

As the fundamental equations in quantum mechanics, nonlinear Schrödinger (NLS) equations are usually chosen as models to describe many different kinds of many-particle quantum systems. One of the most typical examples is the Gross-Pitaevskii (GP) equation [1, 2] which was derived from a mean field approximation and used to describe the Bose-Einstein condensates (BEC) [3–7] for trapped dilute-gas at zero temperature.

GP-equation has been extensively studied during the past decades [8–12]. Numerical analyses have been applied to GP-equation to investigate the dynamics of BEC [8, 9]; analytical methods have also been used for solving the GP-equation to predict properties of the condensates [10], and rigorous mathematical proof has been provided to guarantee the existence of travelling wave solutions to the GP-equation [11, 12].

Apart from these studies, work related with utilizing the generalized GP-equation to investigate physical phenomena still attracts much attention [13–16]. Coste [13] derived a generalized GP-equation from the correction for the Lagrangian of the original GP-model and this model can describe both the two-fluid model and the Hills-Roberts model under two circumstances. By particle-number-conserving Bogoliubov method, Gardiner [14] demonstrated the validity of the time-dependent GP-equation for a highly condensed Bose gas. And with an equivalent method, Castin and Dum [15] obtained a generalized GP-equation which can yield both the time-dependent GP-equation for the condensate wave function and the linear dynamics of noncondensed particles in two situations. Furthermore, building on the works of Gardiner [14] and Castin and Dum [15], Gardiner and Morgan [16] derived a generalized GP-equation which can describe the condensate and noncondensate dynamics of Bose-Einstein dilute atomic gas at finite temperature.

Similarly, in this paper, we also acquire a generalized GP-equation. In the following we will outline the aim of this work.

It is well known that GP-equation has a wide range of validity provided that the scattering length (denoted by a) is much smaller than the average distance between particles (denoted by d). In the repulsive case [3, 4], from the physics point of view, the atom-atom interaction is effectively weak and dominated by the s-wave scattering, so the realistic interaction between particles can be well approximated by the s-wave scattering [17]. On the other hand, from the mathematics point of view, the solution to GP-equation is well defined in the repulsive case (i.e., a > 0) since there exists only one global solution to GP-equation; see [18–24] for more detail.

However, GP-equation is not consistent very well with the attractive case [4]. For the attractive case (i.e., a < 0), blow-up (collapse) may take place in the 2D and 3D cases, see [25–30]. In fact, as the temperature approaches to zero, the kinetic energy be small, which implies that blow-up deduced mathematically from GP-equation never happens in the experiments. Therefore, GP-model is not a correct model for describing the attractive case since it violates the compatibility of physical fact and mathematical result. To give a reasonable model which is compatible with physical fact and mathematical result is one of the motivations for this manuscript.

And to give a model which includes both effects of the s-wave scattering and the atom-atom interaction to describe more general many-particle quantum system near zero temperature is another motivation for this manuscript. It is noted that the atom-atom interaction can not be neglected when the scattering length is not much smaller than the average distance between particles. In this situation, GP-equation is not a good model to describe general many-particle quantum system.

In this paper, we establish an NLS model for more general many-particle quantum systems. Different from the interactions considering in GP-equation, the interactions among particles in the NLS model include both the s-wave scattering and the atom-atom interaction. And we will see later (Theorem 3.1) that there exists a global solution for the NLS model and no blow-up takes place. Furthermore, we will show that the NLS model can be regarded as a generalization of GP-equation. In the end, we prove that the Hamilton energy and the total particle number both are conservative quantities.

This paper is organized as follows. Section 2 derives the new Hamilton energy from the correction of the original one and obtains the NLS model. Section 3 proves rigorously the global existence of solution to the model and obtains the expression of the solution. Section 4 verifies that the conservation laws hold true. Section 5 discusses some existing approaches and compares them with ours. And Section 6 is devoted to the conclusions.

2. The NLS Model for Many-Particle Quantum Systems

In order to obtain the NLS model, we take two steps. At first, we derive the new Hamilton energy from the correction of the original one. And then the NLS model can be obtained by applying the theory of quantum physics to the Hamiltonian.

At first, we recall the original GP-equation as follows:

()

where m the boson mass, ℏ Planck constant, V(x) the external trapping potential, |ψ|² the density of bosons, and U the interaction “strength”, given by

()

where a is the s-wave scattering length with following physical interpretation:

()

Also, we note that the corresponding Hamilton energy of (2.1) as follows:

()

where the first term in (2.4), that is,

()

represents the kinetic energy of bosons, the second term in (2.4), that is,

()

represents the external trapping potential energy and the last term in (2.4), that is,

()

represents the bosons interaction potential energy.

Since the physical interpretation of the kinetic energy (2.5) and the external trapping potential energy (2.6) of GP-equation are the same as those of the NLS model and the only difference between them is the interaction potential energy, the Hamilton energy of the NLS model can be expressed as follows:

()

where function g(·) : R⁺ → R is a C¹ function undetermined. Some essential information of function g can be derived from the following analysis.

For the NLS model, the interaction potential energy is built on the basis of the wave-particle duality in quantum mechanics, the assumptions that the atom-atom interaction be chosen to be the van der Waals force [31, 32], and the interaction potential energy is changed continuously with density of particles.

The wave-particle duality in quantum mechanics points out that the many-particle quantum system has both the properties of wave and particle, which implies that the interactions among particles include both of the s-wave scattering and the atom-atom interaction. The interaction mechanisms of the former are the same as wave but the mechanisms of the latter are the same as particle. More precisely, if the scattering length is much smaller than the average distance between particles (i.e., a ≪ d), the s-wave scattering takes the leading role, and if the scattering length is much bigger than the average distance between particles (i.e., a ≫ d), the atom-atom interaction plays dominant role, or else the two both work.

If the scattering length is much smaller than the average distance between particles (i.e., a ≪ d), the realistic interaction between particles can be approximated by the s-wave scattering as shown in (2.7), then we can infer from (2.7) that g(z) and z follow the linear relationship, that is,

()

for general many-particle quantum systems provided that 0 ≤ z ≤ ρ₀, where ρ₀ ∈ R⁺ is sufficiently small constant since the trapped gas is dilute and c₀ ∈ R⁺ or c₀ ∈ R⁻ corresponds to repulsive and attractive case, respectively.

If the scattering length is much bigger than the average distance between particles (i.e., a ≫ d), the atom-atom interaction is chosen to be the van der Waals interaction, see [31, 32] and the references therein and the relationship between the atom-atom interaction potential energy and the average distance between particles can be depicted as shown in the Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The atom-atom interaction potential energy as a function of the average distance between particles.

Since the average distance between particles and the density of particles are subject to conservation of mass, the relationship between them satisfies

()

then together with Figure 1 the relationship between the atom-atom interaction potential energy and the density of particles can be derived as shown in the Figure 2.

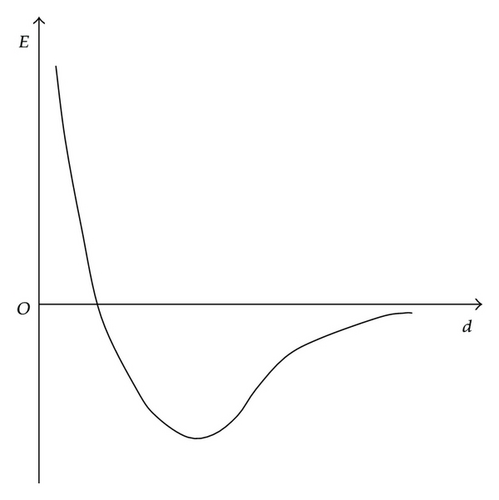
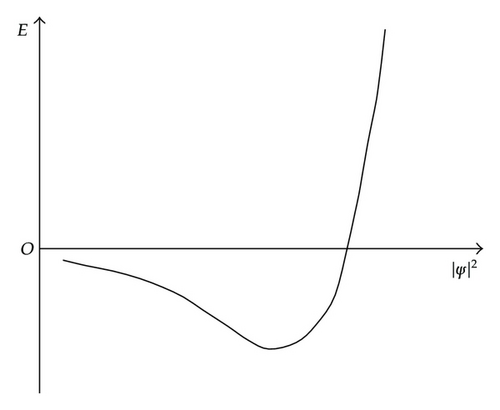
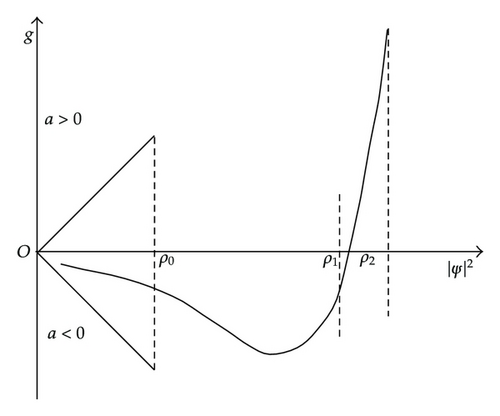
Combining relationship (2.9) with Figure 2, we can get the effects of the s-wave scattering and the van der Waals interaction as shown in the Figure 3; (0, ρ₀) is the domain in which the s-wave scattering takes the leading role, (ρ₁, ρ₂) is the domain in which the van der Waals force plays the dominant role, and (ρ₀, ρ₁) is the domain in which the two both work.

Considering both effects of the s-wave scattering and the van der Waals interaction and the assumption that the interaction potential energy is changed continuously with density of particles, we take function g as shown in the Figure 4.

Although the exact formula of g(z) can not be obtained from Figure 4, noting the fact that the density of particles in experiments never is infinite and bounded above, that is,

()

the following conditions hold true:

()

where c₁ is a positive constant and

()

where g₁(z), g₂(z) are C¹ functions and g₂ satisfies

()

where c₂, c₃, c₄, c₅ are all positive constants.

The physical conditions (2.12) and (2.13) can be written as the following mathematical form:

()

where g₁(z), g₂(z) are C¹ functions and g₂ satisfies

()

According to the theory of quantum physics, that is,

()

we obtain the NLS model as follows:

()

where Ω be a bounded open set in Rⁿ(n ≤ 3) and (x, t) ∈ Ω × (0, ∞).

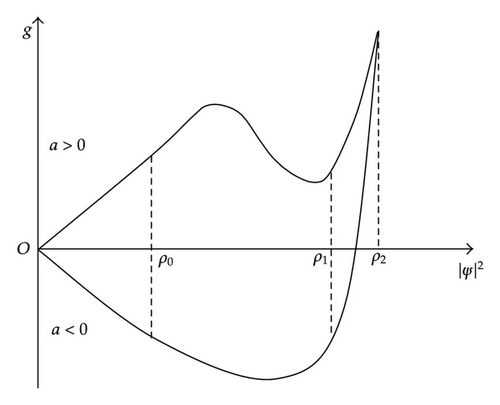
Since |ψ|² < ρ₀ implies that the gas is dilute, the atom-atom interaction is effectively weak and the realistic interaction between particles can be approximated by the s-wave scattering. Under this condition and taking c₀ = 2πaℏ²/m in (2.19), the NLS model (2.19) yields the GP-equation, which implies that (2.19) can be regarded as a generalization of the GP-equation.

3. Mathematical Results of the NLS Model

For the NLS model (2.19), we have the following global existence result.

Theorem 3.1. Assume that g satisfies conditions (2.15), (2.16) and (2.17), if V(x) ∈ L²(Ω), then for any ψ₀ ∈ H¹(Ω, C), there exists a global solution to (2.19) in C⁰([0, ∞), L²(Ω, C))∩L^∞((0, ∞), H¹(Ω, C)). Furthermore, for all (x, t) ∈ Ω × [0, ∞), the solution can be expressed as follows:

()

where

()

Proof. Firstly, we prove the global existence of solution to (2.19) in L^∞((0, ∞), H¹(Ω, C)) by Galerkin method.

Let ψ = u₁ + iu₂, by the theory of infinite dimensional Hamilton system proposed by Ma [24], (2.19) be equivalent to the following equations:

()

where

()

Let , X : = L²(Ω, R²) and choose as orthonormal basis of space L²(Ω).

Set X_n, as follows:

()

Consider the ordinary equations as follows:

()

where

By the theory of ordinary equations, there exists only one local solution of (3.6):

()

From (3.6) we can obtain the equality

()

which holds true for any

, where

()

Moreover, equality

()

holds true for any

Put into (3.10), we obtain that

()

which implies

()

Next, we claim that

()

Since (2.16) and (2.17) holds true; we have the following result:

()

then there exists a positive number ρ₃, such that

()

If |ψ|² > ρ₃, by Poincaré’s inequality and Young’s inequality (3.13) holds true; on the other hand, if |ψ|² ≤ ρ₃, then ∫_Ω (1/2h)g(|ψ|²) | ψ|²dx be bounded below, by Poincaré’s inequality and Young’s inequality (3.13) also holds true.

Since (3.12) and (3.13) hold true, then {(u_n, v_n)} is bounded in L^∞((0, ∞), X₁). Therefore there exists a subsequence, we still write it as , such that

()

By (2.15), (2.16), and (2.17); and Rellich-Kondrachov Compactness Theorem, we know operator

()

is weakly continuous.

Let n → ∞ in (3.8), following equality:

()

holds true for any

Since is dense in , equality (3.18) holds true for all , which implies that (u, v) ∈ L^∞((0, ∞), X₁) is a global solution of (3.3), then ψ = u + iv ∈ L^∞((0, ∞), H¹(Ω, C)) is a global solution of (2.19).

At last, we prove the global solution ψ = u + iv of (2.19) is in C⁰([0, ∞), L²(Ω, C)) by semigroup theory.

Set operator

()

Since the following equality:

()

holds true for any (u₁, u₂), (ω₁, ω₂) ∈ X₁, then operator

is an antisymmetric operator. By Stone Theorem, operator A is a generator of an unitary semigroup and the unitary semigroup can be represented as follows:

()

The solution of (3.3) can be represented as follows:

()

where

()

By (2.15), (2.16), and (2.17); and Gagliardo-Nirenberg-Sobolev inequality, we obtain that the global solution of (3.3) satisfies (u, v) ∈ C⁰([0, ∞), X), which implies ψ = u + iv ∈ C⁰([0, ∞), L²(Ω, C)).

Furthermore, the solution ψ can be expressed as follows:

()

Remark 3.2. In [24], it was proved that all dynamic equations in quantum physics, that is,

()

can be equivalently expressed as the following Hamilton form:

()

where H the Hamilton energy, ψ_k the wave function and

4. The Conservation Laws

For the NLS model (2.19), we prove that the Hamilton energy and the total particle number both are conservative quantities.

Theorem 4.1. Assume that g satisfies conditions (2.15), (2.16) and (2.17), if V(x) ∈ L²(Ω), then for any ψ₀ ∈ H¹(Ω, C), there exist two conservative quantities for (2.19): the energy

()

and the total particle number

()

Proof. Since ψ = u + iv is the solution of (2.19), then (u, v) is the solution of (3.3) and we have the following equalities:

()

which imply that the energy H and the total particle number N both are conservative quantities of (2.19).

5. Discussion

Taking the dense fluid of strongly interacting bosons as mixture of normal fluid and superfluid, and substituting the rule of Galilean invariance for local gauge invariance, Coste [13] made correction for the Lagrangian of the original GP-model by adding the degrees of freedom corresponding to the normal fluid. As a result, they obtained the generalized GP-equation which can describe both the two-fluid model and the Hills-Roberts model under two different circumstances.

Building on the works of Gardiner [14] and Castin and Dum [15], Gardiner and Morgan [16] derived the generalized GP-equation which can describe the condensate and noncondensate dynamics of Bose-Einstein dilute atomic gas at finite temperature. It is worthwhile to mention that unlike using expansion in inverse powers of the total number of particles in [14], Gardiner and Morgan [16] used expansion in powers of ration of noncondensate to condensate particle numbers and constructed the approximate Hamiltonian of third-order.

As the same as the above works [13, 16], the manuscript presented here also derive the generalized GP-equation from the correction of the original Hamiltonian. In addition, collapse (blow up) is prevented for our model and also for condensate and noncondensate dynamic model [16] when accounting for fluctuations.

But differences do exist. One of the differences is that the two above works are based on the classification of the state of particle (or the state of fluid), that is, condensate and noncondensate (or normal fluid and superfluid), but ours focus on the classification of interaction of particles, that is, the s-wave scattering and the atom-atom interaction. And another difference is the mechanism on which above related models build. The two-fluid model [13] respect Galilean invariance rule. The condensate and noncondensate dynamic model [16] obey the formalism of number-conserving. However, our model builds on the basis of the wave-particle duality in quantum mechanics.

It must be pointed out that our model is valid only on three assumptions. One is that the interactions among particles include only two effects: the s-wave scattering and the atom-atom interaction. Consequently, there is no other effect. Another one is that atom-atom interaction be chosen to be the van der Waals force. And the third one is that the interaction potential energy is changed continuously with density of particles.

Meanwhile, it is that the global solution to the NLS model is well defined and collapse (blow-up) is prevented guaranteeing the model is reasonable from the mathematical viewpoint, but further physical experiments should be done to verify this model. Especially, data from future experiments combining with the conditions (2.15) and (2.16) may give the exact expression of function g.

Inspired by the classification of the state of particle (i.e., condensate and noncondensate) in works [9, 10, 15, 16], and taking into account of the classification of the interaction of particles (i.e., the s-wave scattering and the atom-atom interaction), further investigation on the model of general many-particle quantum systems is necessary in future.

6. Conclusions

Building on the basis of the wave-particle duality in quantum mechanics and assumption that the interactions among particles include only two effects: the s-wave scattering and the atom-atom interaction, we derive the new Hamilton energy from the correction of the original one. From the new Hamiltonian we derive the NLS model for more general many-particle quantum systems. Expression of the global solution to the NLS model is obtained. Collapse (blow-up) is prevented for the model. Conservation laws hold true both for the Hamilton energy and the total particle number.

Acknowledgments

The authors are grateful to the anonymous referees whose careful reading of the paper and valuable comments were very helpful for revising and improving our work, as well as for bringing references [9, 16] to our attention. This work is supported by the Scientific Research Foundation of Civil Aviation Flight University of China (J2011-30).

References

1 Gross E. P., Structure of a quantized vortex in boson systems, Nuovo Cimento. (1961) 20, 454–477, 0128907, https://doi.org/10.1007/BF02731494, ZBL0100.42403.
10.1007/BF02731494
Web of Science® Google Scholar
2 Pitaevskii L. P., Vortex lines in an imperfect Bose gas, Soviet Physics Journal. (1961) 13, 451–454.
Web of Science® Google Scholar
3 Anderson M. H., Ensher J. R., Matthews M. R., Wieman C. E., and Cornell E. A., Observation of Bose-Einstein condensation in a dilute atomic vapor, Science. (1995) 269, no. 5221, 198–201, 2-s2.0-11944274056, https://doi.org/10.1126/science.269.5221.198.
10.1126/science.269.5221.198
CAS PubMed Web of Science® Google Scholar
4 Bradley C. C., Sackett C. A., Tollett J. J., and Hulet R. G., Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions, Physical Review Letters. (1995) 75, no. 9, 1687–1690, 2-s2.0-4243132347, https://doi.org/10.1103/PhysRevLett.75.1687.
10.1103/PhysRevLett.75.1687
CAS PubMed Web of Science® Google Scholar
5 Davis K. B., Mewes M. O., Andrews M. R., Van Druten N. J., Durfee D. S., Kurn D. M., and Ketterle W., Bose-Einstein condensation in a gas of sodium atoms, Physical Review Letters. (1995) 75, no. 22, 3969–3973, 2-s2.0-4244115335, https://doi.org/10.1103/PhysRevLett.75.3969.
10.1103/PhysRevLett.75.3969
CAS PubMed Web of Science® Google Scholar
6 Dalfovo F., Giorgini S., Pitaevskii L. P., and Stringari S., Theory of Bose-Einstein condensation in trapped gases, Reviews of Modern Physics. (1999) 71, no. 3, 463–512, 2-s2.0-0033246313, https://doi.org/10.1103/RevModPhys.71.463.
10.1103/RevModPhys.71.463
CAS Web of Science® Google Scholar
7 Leggett A. J., Bose-Einstein condensation in the alkali gases: some fundamental concepts, Reviews of Modern Physics. (2001) 73, no. 2, 307–356, 2-s2.0-0035535327, https://doi.org/10.1103/RevModPhys.73.307.
10.1103/RevModPhys.73.307
CAS Web of Science® Google Scholar
8 Adhikari S. K. and Muruganandam P., Bose-Einstein condensation dynamics from the numerical solution of the Gross-Pitaevskii equation, Journal of Physics B. (2002) 35, no. 12, 2831–2843, 2-s2.0-0037188919, https://doi.org/10.1088/0953%2D4075/35/12/317.
10.1088/0953-4075/35/12/317
CAS Web of Science® Google Scholar
9 Bao W., Jaksch D., and Markowich P. A., Numerical solution of the Gross-Pitaevskii equation for Bose-Einstein condensation, Journal of Computational Physics. (2003) 187, no. 1, 318–342, https://doi.org/10.1016/S0021%2D9991(03)00102%2D5, 1977789, ZBL1028.82501.
10.1016/S0021-9991(03)00102-5
Web of Science® Google Scholar
10 Trallero-Giner C., Drake J., Lopez-Richard V., Trallero-Herrero C., and Birman J. L., Bose-Einstein condensates: analytical methods for the Gross-Pitaevskii equation, Physics Letters A. (2006) 354, no. 1-2, 115–118, 2-s2.0-33646095793, https://doi.org/10.1016/j.physleta.2006.01.032.
10.1016/j.physleta.2006.01.032
CAS Web of Science® Google Scholar
11 Chiron D., Travelling waves for the Gross-Pitaevskii equation in dimension larger than two, Nonlinear Analysis: Theory, Methods & Applications.(2004) 58, no. 1-2, 175–204, https://doi.org/10.1016/j.na.2003.10.028, 2070812, ZBL1054.35091.
10.1016/j.na.2003.10.028
Web of Science® Google Scholar
12 Béthuel F., Gravejat P., and Saut J.-C., Travelling waves for the Gross-Pitaevskii equation. II, Communications in Mathematical Physics. (2009) 285, no. 2, 567–651, https://doi.org/10.1007/s00220%2D008%2D0614%2D2, 2461988, ZBL1190.35196.
10.1007/s00220-008-0614-2
Web of Science® Google Scholar
13 Coste C., Nonlinear Schrödinger equation and superfluid hydrodynamics, The European Physical Journal B. (1998) 1, no. 2, 245–253, https://doi.org/10.1007/s100510050178, 1646182.
10.1007/s100510050178
CAS Web of Science® Google Scholar
14 Gardiner C. W., Particle-number-conserving Bogoliubov method which demonstrates the validity of the time-dependent Gross-Pitaevskii equation for a highly condensed Bose gas, Physical Review A. (1997) 56, no. 2, 1414–1423, 2-s2.0-0000935910, https://doi.org/10.1103/PhysRevA.56.1414.
10.1103/PhysRevA.56.1414
CAS Web of Science® Google Scholar
15 Castin Y. and Dum R., Low-temperature Bose-Einstein condensates in time-dependent traps: beyond the U(1) symmetry-breaking approach, Physical Review A. (1998) 57, no. 4, 3008–3021, 2-s2.0-0001053337, https://doi.org/10.1103/PhysRevA.57.3008.
10.1103/PhysRevA.57.3008
CAS Web of Science® Google Scholar
16 Gardiner S. A. and Morgan S. A., Number-conserving approach to a minimal self-consistent treatment of condensate and noncondensate dynamics in a degenerate Bose gas, Physical Review A. (2007) 75, no. 4, 20, 043621, 2-s2.0-34548145771, https://doi.org/10.1103/PhysRevA.75.043621.
10.1103/PhysRevA.75.043621
Web of Science® Google Scholar
17 Parkins A. S. and Walls D. F., The physics of trapped dilute-gas Bose-Einstein condensates, Physics Reports. (1998) 303, no. 1, 1–80, https://doi.org/10.1016/S0370%2D1573(98)00014%2D3.
10.1016/S0370-1573(98)00014-3
CAS Web of Science® Google Scholar
18 Anton R., Global existence for defocusing cubic NLS and Gross-Pitaevskii equations in three dimensional exterior domains, Journal de Mathématiques Pures et Appliquées. (2008) 89, no. 4, 335–354, https://doi.org/10.1016/j.matpur.2007.12.006, 2401142, ZBL1148.35081.
10.1016/j.matpur.2007.12.006
Web of Science® Google Scholar
19 Gérard P., The Cauchy problem for the Gross-Pitaevskii equation, Annales de l′Institut Henri Poincaré. (2006) 23, no. 5, 765–779, https://doi.org/10.1016/j.anihpc.2005.09.004, 2259616, ZBL1122.35133.
10.1016/j.anihpc.2005.09.004
Google Scholar
20 Hao C., Hsiao L., and Li H.-L., Global well posedness for the Gross-Pitaevskii equation with an angular momentum rotational term in three dimensions, Journal of Mathematical Physics. (2007) 48, no. 10, https://doi.org/10.1063/1.2795218, 2362770, ZBL1152.81463.
10.1063/1.2795218
Web of Science® Google Scholar
21 Lieb E. H. and Seiringer R., Proof of Bose-Einstein condensation for dilute trapped gases, Physical Review Letters. (2002) 88, no. 17, 2-s2.0-0037193018.
10.1103/PhysRevLett.88.170409
Web of Science® Google Scholar
22 Lieb E. H., Seiringer R., Solovej J. P., and Yngvason J., The Mathematics of the Bose Gas and Its Condensation, 2005, Birkhäuser, Basel, Switzerland, 2143817.
Google Scholar
23 Lieb E. H. and Seiringer R., Derivation of the Gross-Pitaevskii equation for rotating Bose gases, Communications in Mathematical Physics. (2006) 264, no. 2, 505–537, https://doi.org/10.1007/s00220%2D006%2D1524%2D9, 2215615, ZBL1233.82004.
10.1007/s00220-006-1524-9
Web of Science® Google Scholar
24 Ma T., Theory and Methods For Partial Differential Equations, 2011, Science Press, Beijing, China, In Chinese.
Google Scholar
25 Carles R., Remarks on nonlinear Schrödinger equations with harmonic potential, Annales Henri Poincaré. (2002) 3, no. 4, 757–772, https://doi.org/10.1007/s00023%2D002%2D8635%2D4, 1933369, ZBL1021.81013.
10.1007/s00023-002-8635-4
Web of Science® Google Scholar
26 Carles R., Critical nonlinear Schrödinger equations with and without harmonic potential, Mathematical Models & Methods in Applied Sciences. (2002) 12, no. 10, 1513–1523, https://doi.org/10.1142/S0218202502002215, 1933935, ZBL1029.35208.
10.1142/S0218202502002215
Web of Science® Google Scholar
27 Tsutsumi Y., Rate of L² concentration of blow-up solutions for the nonlinear Schrödinger equation with critical power, Nonlinear Analysis: Theory, Methods & Applications. (1990) 15, no. 8, 719–724, https://doi.org/10.1016/0362%2D546X(90)90088%2DX, 1074950, ZBL0726.35124.
10.1016/0362-546X(90)90088-X
Web of Science® Google Scholar
28 Tsurumi T. and Wadati M., Stability of the D-dimensional nonlinear Schrödinger equation under confined potential, Journal of the Physical Society of Japan. (1999) 68, no. 5, 1531–1536, 2-s2.0-0033470462, https://doi.org/10.1143/JPSJ.68.1531, ZBL0974.35117.
10.1143/JPSJ.68.1531
CAS Web of Science® Google Scholar
29 Zhang J., Stability of attractive Bose-Einstein condensates, Journal of Statistical Physics. (2000) 101, no. 3-4, 731–746, https://doi.org/10.1023/A:1026437923987, 1804895, ZBL0989.82024.
10.1023/A:1026437923987
Web of Science® Google Scholar
30 Zhang J., Sharp threshold for blowup and global existence in nonlinear Schrödinger equations under a harmonic potential, Communications in Partial Differential Equations. (2005) 30, no. 10–12, 1429–1443, https://doi.org/10.1080/03605300500299539, 2182299.
10.1080/03605300500299539
Web of Science® Google Scholar
31 Das T. K., Kundu A., Canuto S., and Chakrabarti B., ⁸⁵Rb Bose-Einstein condensate with tunable interaction: a quantum many body approach, Physics Letters A. (2009) 373, no. 2, 258–261, 2-s2.0-57549091758, https://doi.org/10.1016/j.physleta.2008.10.092.
10.1016/j.physleta.2008.10.092
CAS Web of Science® Google Scholar
32 Tewari S. P., Silotia P., Saxena A., and Gupta L. K., Effect of incorporating three-body interaction in the low-density energy expansion of Bose-Einstein condensate of ⁸⁷Rb atoms trapped in a harmonic potential, Physics Letters A. (2006) 359, no. 6, 658–662, 2-s2.0-33750365737, https://doi.org/10.1016/j.physleta.2006.07.027.
10.1016/j.physleta.2006.07.027
CAS Web of Science® Google Scholar

Citing Literature

All articles

A Nonlinear Schrödinger Model for Many-Particle Quantum Systems

Abstract

1. Introduction

2. The NLS Model for Many-Particle Quantum Systems

3. Mathematical Results of the NLS Model

4. The Conservation Laws

5. Discussion

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Nonlinear Schrödinger Model for Many-Particle Quantum Systems

Abstract

1. Introduction

2. The NLS Model for Many-Particle Quantum Systems

3. Mathematical Results of the NLS Model

4. The Conservation Laws

5. Discussion

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information