The steady boundary layer flow and heat transfer of a viscous fluid on a moving flat plate in a parallel free stream with variable fluid properties are studied. Two special cases, namely, constant fluid properties and variable fluid viscosity, are considered. The transformed boundary layer equations are solved numerically by a finite-difference scheme known as Keller-box method. Numerical results for the flow and the thermal fields for both cases are obtained for various values of the free stream parameter and the Prandtl number. It is found that dual solutions exist for both cases when the fluid and the plate move in the opposite directions. Moreover, fluid with constant properties shows drag reduction characteristics compared to fluid with variable viscosity.

1. Introduction

The problem of forced convection flow and heat transfer past a continuously moving flat plate is a classical problem of fluid mechanics and has attracted considerable interest of many researchers not only because of its many practical applications in various extrusion processes but also because of its fundamental role as a basic flow problem in the boundary layer theory of Newtonian and non-Newtonian fluid mechanics. It has been solved for the first time in 1961 by Sakiadis [1]. Thereafter, many solutions have been obtained for different situations of this class of boundary layer problems. The solutions for the cases when the mass transfer effect is included (fluid injection and fluid suction), chemical effects are considered, constant or variable surface temperatures, and other situations have been reported by Klemp and Acrivos [2], Abdelhafez [3], Hussaini et al. [4], Afzal et al. [5], Bianchi and Viskanta [6], Lin and Huang [7], Chen [8], Magyari and Keller [9], Afzal [10], Fang [11, 12], Sparrow and Abraham [13], and Weidman et al. [14], among others. However, it seems that the existence of dual solutions was reported only in the papers by Afzal et al. [5], Afzal [10], Fang [11, 12], Weidman et al. [14], Riley and Weidman [15], Fang et al. [16] and Ishak et al. [17].

The work by Pop et al. [18] belongs to the above class of problems, including the variation of fluid viscosity with temperature. The authors obtained similarity solutions considering that viscosity varies as an inverse function of temperature for two distinct Prandtl numbers 0.7 and 10.0. Exactly the same approach was taken by Elbashbeshy and Bazid [19] who reported results for Prandtl numbers 0.7 and 7.0. Pantokratoras [20] reconsidered the problem investigated earlier by Pop et al. [18] with the view to allow for the temperature-dependency on the Prandtl number. Fang [21] studied the influences of temperature-dependent fluid properties on the boundary layers over a continuously stretching surface with constant temperature. Andersson and Aarseth [22] presented a rigorous approach for proper treatment of variable fluid properties in the Sakiadis [1] flow problem. They presented a generalized similarity transformation which enables the analysis of the influence of temperature-dependent fluid properties. New and interesting results for water at atmospheric pressure were reported. The objective of the present paper is, therefore, to extend the paper by Andersson and Aarseth [22] to the case when the plate moves in a parallel free stream, a case that has not been considered before in the literature. Thus, following Andersson and Aaresth [22], the governing partial differential equations are transformed using similarity transformation to a system of ordinary differential equations, which is more convenient for numerical computations. The transformed nonlinear ordinary differential equations are solved numerically for certain values of the governing parameters using the Keller-box method. This method has been very successfully used by the present authors for other fundamental problems, see Ishak et al. [23] and Bachok et al. [24, 25].

2. Problem Formulation

Consider a steady two-dimensional boundary layer flow on a fixed or continuously moving flat plate in a parallel free stream of a viscous fluid. It is assumed that the plate moves with a constant velocity U_w in the same or opposite directions to the free stream of constant velocity U₀. The ambient fluid and the moving plate are kept at constant temperatures T₀ and T_w, where T_w > T₀ (heated plate). Under these conditions, the boundary layer equations of this problem are given by, see Andersson and Aarseth [22],

()

subject to the boundary conditions

()

where x and y are coordinates measured along the surface and normal to it, respectively. Further, u and v are the velocity components in the x and y directions, respectively, T is the fluid temperature, ρ is the fluid density, μ is the dynamic viscosity, k is the thermal conductivity and C_p is the specific heat at constant pressure. The similarity variable η and the new dependent variables f and θ are defined as, see Andersson and Aarseth [22],

()

where U = U_w + U₀, a is a dimensionless positive constant, and ψ is the stream function, which is defined as

()

Further, ρ₀, μ₀, k₀, C_p0, and υ₀ are the values of the fluid properties of the ambient fluid, that is, at temperature T₀. Using (2.3)–(2.5), the partial differential equation (2.1) can be reduced to the following nonlinear ordinary differential equations

()

where Pr₀ is the constant Prandtl number of the ambient fluid and primes denote differentiation with respect to η. Equations (2.7) and (2.8) are subjected to the boundary conditions (2.2), which become

()

where ε is the free stream parameter since it gives the relative importance of the free stream velocity and is defined as

()

It should be mentioned that ε = 1/2 corresponds to a free stream velocity equal to the moving plate velocity, ε = 1 corresponds to the classical Blasius flow, and ε = 0 is for the case of a moving flat plate in a quiescent fluid (Sakiadis flow). Thus, for ε = 0, (2.7) and (2.8) along with the boundary conditions (2.9) reduce to (2.9)–(2.11) of the paper by Andersson and Aarseth [22]. The case where both the free stream and the plate velocities are in the same direction corresponds to 0 < ε < 1. If ε > 1, the free stream is directed towards the positive x-direction while the plate moves towards the negative x-direction. If ε < 0, the free stream is directed towards the negative x-direction while the plate moves towards the positive x-direction (see Afzal et al. [5]). However, in this paper, we consider only the case ε ≥ 0, that is the free stream is fixed (towards the positive x-direction).

The physical quantities of interest are the surface shear stress τ_w and the surface heat flux q_w, which can be expressed as

()

3. Special Cases

3.1. Constant Fluid Properties (Case A)

In this case, the similarity variable η defined in (2.3) simplifies to the Blasius [26] variable

()

and (2.7) and (2.8) reduce to

()

which are still subjected to the boundary conditions (2.9). (3.2) is the extended Blasius equation, where the solution subjected to the boundary conditions (2.9) when ε = 1 was reported by Fang [27].

3.2. Variable Viscosity (Case B)

Pop et al. [18] allowed only for a temperature, dependent viscosity, whereas the other fluid properties were assumed to be constant. This assumption was then followed by Elbashbeshy and Bazid [19] and Pantokratoras [20]. In this approximation, the similarity variable (2.3) simplifies to (3.1) and the momentum boundary layer (2.7) becomes

()

Following the form of the variable viscosity μ(T) proposed by Lai and Kulacki [28], and used by Pop et al. [18] and Andersson and Aarseth [22], we take μ(T) as

()

where γ is a fluid property, which depends on the reference temperature T_ref. In general, the viscosity of liquids decreases with increasing temperature (γ > 0), whereas it increases for gases (γ < 0). However, if the reference temperature is taken as T₀, the relation (3.5) can be written as

()

where θ_ref is a dimensionless constant defined as θ_ref ≡ −1/[(T_w − T₀) γ] and T_w − T₀ is the operating temperature difference Δ T.

4. Results and Discussion

The nonlinear ordinary differential equations (3.2) or (3.4), depending on the actual case considered, along with (3.3) subject to the boundary conditions (2.9) were solved numerically using a very efficient implicit finite-difference scheme known as Keller-box method, which is very well described in the book by Cebeci and Bradshaw [29]. In the general context, empirical correlations for all required fluid properties can be recast in terms of the dimensionless temperature θ(η) as defined in (2.5). The proper relations take then the forms like, for example (3.6). The generalized boundary value problem (2.7)–(2.9) is apparently a three-parameter problem of which the solution depends on T₀, and ΔT ≡ T_w − T₀, together with the Prandtl number Pr₀ of the ambient fluid. The Prandtl number Pr₀ is, however, uniquely related to the ambient temperature T₀ and the boundary value problem (2.7)–(2.9) is actually a two-parameter problem in T₀ (or Pr₀) and ΔT. The present paper focuses on the effects of a temperature-dependent viscosity only, and the other fluid properties are assumed to be constant. First, however, the numerical solution of the classical problem (moving plate in a quiescent fluid, ε = 0) with constant fluid properties was computed for Prandtl number Pr₀ = 0.7, 1, and 10. The characteristic surface gradients f^′′(0) and θ′(0) are compared with Andersson and Aarseth [22] in Table 1 and serve primarily to validate the accuracy of the present solution technique. In order to illustrate the effect of a temperature-dependent viscosity, two different cases have been solved. The ambient fluid considered is water at temperature T₀ = 278 K (5°C) and Pr₀ = 10. The surface temperature is T_w = 358 K (85^°C ) such that the operating temperature difference ΔT ≡ T_w − T₀ is 80 K. Results for problem with constant fluid properties (Case A) are compared with those of the inversely linear viscosity variation (3.5), (3.6) (Case B). In (3.5), (3.6), we set θ_ref = −0.25 for water at T₀ = 278 K, as recommended by Ling and Dybbs [30]. The characteristic surface gradients f^′′(0) and θ′(0) for Pr₀ = 10 are obtained and compared with previously reported cases, and the comparison is shown in Table 2. It is seen from Tables 1 and 2 that the values of f^′′(0) and θ′(0) obtained in this study are in very good agreement with the results reported by Andersson and Aarseth [22]. Therefore, it can be concluded that the developed code can be used with great confidence to study the problem considered in this paper.

Table 1. Values of the reduced skin friction coefficient f^′′(0) and reduced heat flux θ^′(0) at the moving surface for Pr₀ = 0.7,1, and 10 when a = 1 in Case A: constant fluid properties.

ε	Pr₀	a	Andersson and Aarseth [22]		Present results
			−f^′′(0)	−θ^′(0)	−f^′′(0)	−θ^′(0)
0	0.7	1	0.4437483	0.3492365	0.4437	0.3492
0	1	1	—	—	0.4437	0.4437
0	10	1	—	—	0.4437	1.6803

Table 2. Values of the reduced skin friction f^′′(0) and reduced heat flux at the moving surface for Pr₀ = 1, Pr₀ = 10, and a = 1 in both Cases A and B.

ε	Pr₀	a	Andersson and Aarseth [22]		Present results
0	10	1	−f^′′(0)	−θ^′(0)	−f^′′(0)	−θ^′(0)
Case A			0.443748	1.680293	0.4437	1.6803
Case B			1.300553	1.529151	1.3006	1.5292

0	1	1
Case A			—	—	0.4437	0.4437
Case B			—	—	1.0381	0.3181

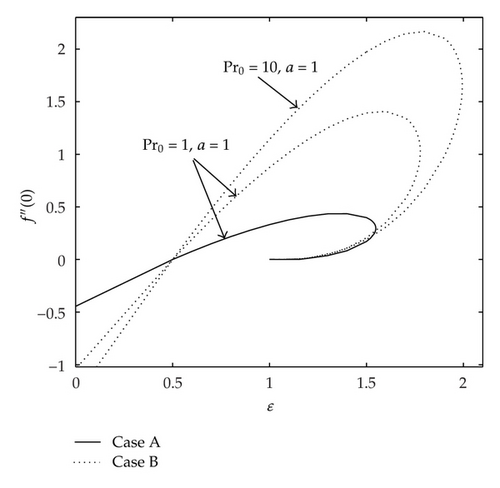
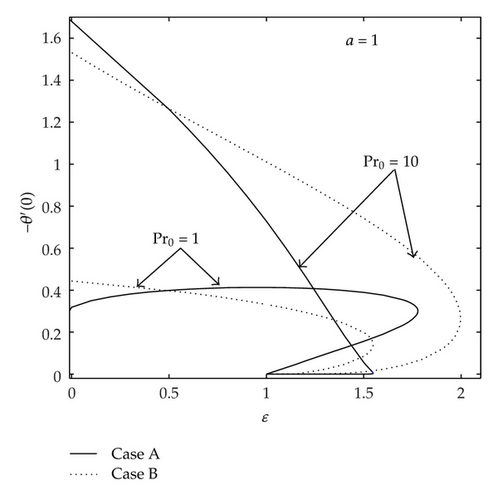
The variations of the reduced skin friction coefficient f^′′(0) and reduced local Nusselt number −θ′(0) with the free stream parameter ε for both Cases (A) and (B) considered are shown in Figures 1 and 2, respectively. The values of f^′′(0) are positive when ε > 0.5, while they are negative when ε < 0.5. Physically, a positive sign of f^′′(0) implies that the fluid exerts a drag force on the plate and a negative sign implies the opposite. It can be seen from these figures that the existence of dual solutions when ε > 1 (the plate moves in the opposite direction of the free stream) with two branch solutions: upper and lower branches. The solution for both Cases (A) and (B) exists up to a critical value of ε (ε_c say). This value of ε_c increases as the Prandtl number Pr is increased, as shown in Figures 1 and 2. Further, it is evident from Figure 1 that the absolute value of f^′′(0) is larger for Case B compared to Case A. Thus, fluid with constant properties shows drag reduction characteristics compared to fluid with variable viscosity. Moreover, the range of ε for which the solution exists is larger for Case B compared to Case A. It is worth mentioning that, for the case of constant fluid properties, Weidman et al. [14] have shown using a stability analysis that the upper branch solutions are stable, while the lower branch solutions are not. We expect that this observation is also true for the present problem.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Variation of the reduced skin friction f^′′(0) with ε for different values of Pr₀ when a = 1. Case A (solid line): constant viscosity and Case B (dotted line): inversely linear viscosity, (3.5), and (3.6).

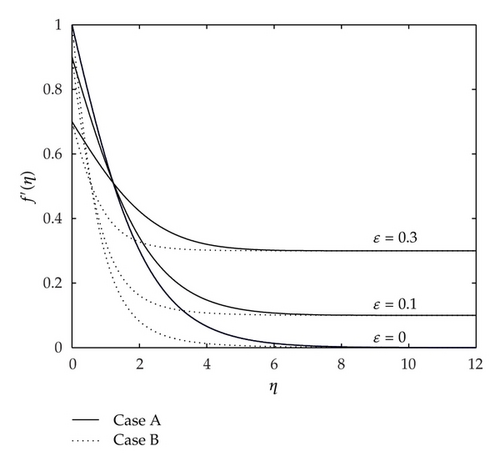
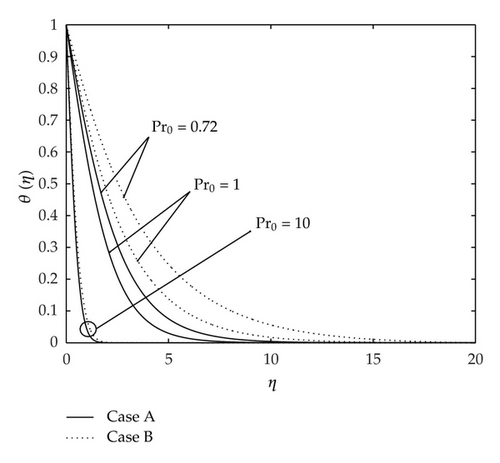
The computed velocity profiles f^′(η) and temperature profiles θ(η) are shown in Figures 3 and 4, respectively. One can see that the velocity profiles f^′(η) in Figure 3 are substantially reduced near the moving surface for Case B as compared with Case A. The moving surface heats the adjacent fluid and thereby reduces its viscosity. Viscous diffusion of streamwise momentum from the surface towards the ambient is accordingly reduced in the inner part of the momentum boundary layer. The temperature profiles in Figure 4 show a higher temperature near the surface due to this reduced viscosity. Figures 3 and 4 show that the far field boundary conditions are approached asymptotically, which support the validity of the numerical results obtained. It is worth mentioning that the results presented in Figures 3 and 4 were produced with η_∞ = 30, much larger than shown in these figures. This integration length is sufficiently long to satisfy f^′′ → 0 and θ′ → 0 which is a necessary condition pointed out by Andersson and Aarseth [22].

5. Conclusions

In the present paper, we have studied numerically the problem of steady boundary layer flow with variable fluid properties on a moving flat plate in a parallel free stream. The governing partial differential equations are transformed using similarity transformation to a more convenient form for numerical computation. The transformed nonlinear ordinary differential equations were solved numerically using the Keller-box method. Numerical results for the skin friction coefficient and the local Nusselt number as well as the velocity and temperature profiles are illustrated in two tables and some graphs for various parameter conditions. Two special cases, namely, constant fluid properties and variable fluid viscosity, were considered. It was found that dual solutions exist when the plate and the free stream move in the opposite directions, for both cases considered. Moreover, fluid with constant properties show drag reduction characteristics compared to fluid with variable viscosity.

Acknowledgments

The authors wish to express their thanks to the reviewers for the valuable comments and suggestions. This work was supported by a research grant (UKM-GUP-2011-202) from the Universiti Kebangsaan Malaysia.

References

1 Sakiadis B. C., Boundary layer behavior on continuous solid surface: the boundary layer on a continuous flat surface, AIChE Journal. (1961) 7, 221–225, https://doi.org/10.1002/aic.690070211.
10.1002/aic.690070211
CAS Web of Science® Google Scholar
2 Klemp J. B. and Acrivos A., A method for integrating the boundary-layer equations through a region of reverse flow, The Journal of Fluid Mechanics. (1972) 53, 177–191, https://doi.org/10.1017/S0022112072000096, ZBL0242.76019.
10.1017/S0022112072000096
Web of Science® Google Scholar
3 Abdelhafez T. A., Skin friction and heat transfer on a continuous flat surface moving in a parallel free stream, International Journal of Heat and Mass Transfer. (1985) 28, no. 6, 1234–1237, 2-s2.0-0022076328, https://doi.org/10.1016/0017%2D9310(85)90132%2D2.
10.1016/0017-9310(85)90132-2
Web of Science® Google Scholar
4 Hussaini M. Y., Lakin W. D., and Nachman A., On similarity solutions of a boundary layer problem with an upstream moving wall, SIAM Journal on Applied Mathematics. (1987) 47, no. 4, 699–709, https://doi.org/10.1137/0147048, 898828, ZBL0634.76034.
10.1137/0147048
Web of Science® Google Scholar
5 Afzal N., Badaruddin A., and Elgarvi A. A., Momentum and heat transport on a continuous flat surface moving in a parallel stream, International Journal of Heat and Mass Transfer. (1993) 36, no. 13, 3399–3403, 2-s2.0-0027656688, https://doi.org/10.1016/0017%2D9310(93)90022%2DX, ZBL0810.76016.
10.1016/0017-9310(93)90022-X
CAS Web of Science® Google Scholar
6 Bianchi M. V. A. and Viskanta R., Momentum and heat transfer on a continuous flat surface moving in a parallel counterflow free stream, Wärme-Und Stoffübertragung. (1993) 29, no. 2, 89–94, 2-s2.0-0037678743, https://doi.org/10.1007/BF01560077.
10.1007/BF01560077
Google Scholar
7 Lin H.-T. and Huang S.-F., Flow and heat transfer of plane surfaces moving in parallel and reversely to the free stream, International Journal of Heat and Mass Transfer. (1994) 37, no. 2, 333–336, 2-s2.0-0028320272, ZBL0803.76077.
10.1016/0017-9310(94)90104-X
CAS Web of Science® Google Scholar
8 Chen C. H., Heat transfer characteristics of a non-isothermal surface moving parallel to a free stream, Acta Mechanica. (2000) 142, no. 1, 195–205, 2-s2.0-0033685675, https://doi.org/10.1007/BF01190018, ZBL0970.76026.
10.1007/BF01190018
Web of Science® Google Scholar
9 Magyari E. and Keller B., Exact solutions for self-similar boundary-layer flows induced by permeable stretching walls, European Journal of Mechanics. B. Fluids. (2000) 19, no. 1, 109–122, https://doi.org/10.1016/S0997%2D7546(00)00104%2D7, 1741018, ZBL0976.76021.
10.1016/S0997-7546(00)00104-7
Web of Science® Google Scholar
10 Afzal N., Momentum transfer on power law stretching plate with free stream pressure gradient, International Journal of Engineering Science. (2003) 41, no. 11, 1197–1207, 2-s2.0-0037411211, https://doi.org/10.1016/S0020%2D7225(03)00002%2D8.
10.1016/S0020-7225(03)00002-8
Web of Science® Google Scholar
11 Fang T., Similarity solutions for a moving-flat plate thermal boundary layer, Acta Mechanica. (2003) 163, no. 3-4, 161–172, 2-s2.0-0041470273, https://doi.org/10.1007/s00707%2D003%2D0004%2Dy, ZBL1064.76031.
10.1007/s00707-003-0004-y
Web of Science® Google Scholar
12 Fang T., Further study on a moving-wall boundary-layer problem with mass transfer, Acta Mechanica. (2003) 163, no. 3-4, 183–188, 2-s2.0-0042973084, https://doi.org/10.1007/s00707%2D002%2D0979%2D9, ZBL1064.76032.
10.1007/s00707-002-0979-9
Web of Science® Google Scholar
13 Sparrow E. M. and Abraham J. P., Universal solutions for the streamwise variation of the temperature of a moving sheet in the presence of a moving fluid, International Journal of Heat and Mass Transfer. (2005) 48, no. 15, 3047–3056, 2-s2.0-18444377413, https://doi.org/10.1016/j.ijheatmasstransfer.2005.02.028, ZBL1189.76143.
10.1016/j.ijheatmasstransfer.2005.02.028
Web of Science® Google Scholar
14 Weidman P. D., Kubitschek D. G., and Davis A. M. J., The effect of transpiration on self-similar boundary layer flow over moving surfaces, International Journal of Engineering Science. (2006) 44, no. 11-12, 730–737, 2-s2.0-33747331317, https://doi.org/10.1016/j.ijengsci.2006.04.005, ZBL1213.76064.
10.1016/j.ijengsci.2006.04.005
CAS Web of Science® Google Scholar
15 Riley N. and Weidman P. D., Multiple solutions of the Falkner-Skan equation for flow past a stretching boundary, SIAM Journal on Applied Mathematics. (1989) 49, no. 5, 1350–1358, https://doi.org/10.1137/0149081, 1015066, ZBL0682.76026.
10.1137/0149081
Web of Science® Google Scholar
16 Fang T., Liang W., and Lee Chia-f.F., A new solution branch for the Blasius equation—a shrinking sheet problem, Computers & Mathematics with Applications. (2008) 56, no. 12, 3088–3095, https://doi.org/10.1016/j.camwa.2008.07.027, 2474564, ZBL1165.76324.
10.1016/j.camwa.2008.07.027
Web of Science® Google Scholar
17 Ishak A., Nazar R., and Pop I., Flow and heat transfer characteristics on a moving flat plate in a parallel stream with constant surface heat flux, Heat and Mass Transfer/Waerme- und Stoffuebertragung. (2009) 45, no. 5, 563–567, 2-s2.0-59449102971, https://doi.org/10.1007/s00231%2D008%2D0462%2D9.
10.1007/s00231-008-0462-9
CAS Web of Science® Google Scholar
18 Pop I., Gorla R. S. R., and Rashidi M., The effect of variable viscosity on flow and heat transfer to a continuous moving flat plate, International Journal of Engineering Science. (1992) 30, no. 1, 1–6, 2-s2.0-0026678379, https://doi.org/10.1016/0020%2D7225(92)90115%2DW.
10.1016/0020-7225(92)90115-W
CAS Web of Science® Google Scholar
19 Elbashbeshy E. M. A. and Bazid M. A. A., The effect of temperature-dependent viscosity on heat transfer over a continuous moving surface, Journal of Physics D. (2000) 33, no. 21, 2716–2721, 2-s2.0-0034323331, https://doi.org/10.1088/0022%2D3727/33/21/309.
10.1088/0022-3727/33/21/309
CAS Google Scholar
20 Pantokratoras A., Further results on the variable viscosity on flow and heat transfer to a continuous moving flat plate, International Journal of Engineering Science. (2004) 42, no. 17-18, 1891–1896, 2-s2.0-4644370480, https://doi.org/10.1016/j.ijengsci.2004.07.005, ZBL1211.76043.
10.1016/j.ijengsci.2004.07.005
Web of Science® Google Scholar
21 Fang T., Influences of fluid property variation on the boundary layers of a stretching surface, Acta Mechanica. (2004) 171, no. 1-2, 105–118, 2-s2.0-5444223017, https://doi.org/10.1007/s00707%2D004%2D0125%2Dy, ZBL1067.76029.
10.1007/s00707-004-0125-y
Web of Science® Google Scholar
22 Andersson H. I. and Aarseth J. B., Sakiadis flow with variable fluid properties revisited, International Journal of Engineering Science. (2007) 45, no. 2–8, 554–561, https://doi.org/10.1016/j.ijengsci.2007.04.012, 2347975, ZBL1213.76062.
10.1016/j.ijengsci.2007.04.012
CAS Web of Science® Google Scholar
23 Ishak A., Nazar R., Bachok N., and Pop I., MHD mixed convection flow near the stagnation-point on a vertical permeable surface, Physica A. (2010) 389, no. 1, 40–46, 2-s2.0-70349563283, https://doi.org/10.1016/j.physa.2009.09.008.
10.1016/j.physa.2009.09.008
Web of Science® Google Scholar
24 Bachok N., Ishak A., and Pop I., Mixed convection boundary layer flow near the stagnation point on a vertical surface embedded in a porous medium with anisotropy effect, Transport in Porous Media. (2010) 82, no. 2, 363–373, https://doi.org/10.1007/s11242%2D009%2D9431%2D0, 2610037.
10.1007/s11242-009-9431-0
Web of Science® Google Scholar
25 Bachok N., Ishak A., and Pop I., Boundary-layer flow of nanofluids over a moving surface in a flowing fluid, International Journal of Thermal Sciences. (2010) 49, no. 9, 1663–1668, 2-s2.0-77955432252, https://doi.org/10.1016/j.ijthermalsci.2010.01.026.
10.1016/j.ijthermalsci.2010.01.026
CAS Web of Science® Google Scholar
26 Blasius H., Grenzschichten in Flüssigkeiten mit kleiner Reibung, Zeitschrift für Angewandte Mathematik und Physik. (1908) 56, 1–37.
Google Scholar
27 Fang T., Guo F., and Lee Chia-f.F., A note on the extended Blasius equation, Applied Mathematics Letters. (2006) 19, no. 7, 613–617, https://doi.org/10.1016/j.aml.2005.08.010, 2224413, ZBL1126.34301.
10.1016/j.aml.2005.08.010
Web of Science® Google Scholar
28 Lai F. C. and Kulacki F. A., The effect of variable viscosity on convective heat transfer along a vertical surface in a saturated porous medium, International Journal of Heat and Mass Transfer. (1990) 33, no. 5, 1028–1031, 2-s2.0-0025434473, https://doi.org/10.1016/0017%2D9310(90)90084%2D8.
10.1016/0017-9310(90)90084-8
Web of Science® Google Scholar
29 Cebeci T. and Bradshaw P., Physical and Computational Aspects of Convective Heat Transfer, 1988, Springer, New York, NY, USA, Springer Study Editions, 969366.
10.1007/978-1-4612-3918-5
Google Scholar
30 Ling J. X. and Dybbs A., The effect of variable viscosity on forced convection over a flat plate submersed in a porous medium, Journal of Heat Transfer. (1992) 114, no. 4, 1063–1065, 2-s2.0-0026953289, https://doi.org/10.1115/1.2911882.
10.1115/1.2911882
CAS Web of Science® Google Scholar

Citing Literature

All articles

Boundary Layer Flow and Heat Transfer with Variable Fluid Properties on a Moving Flat Plate in a Parallel Free Stream

Abstract

1. Introduction

2. Problem Formulation

3. Special Cases

3.1. Constant Fluid Properties (Case A)

3.2. Variable Viscosity (Case B)

4. Results and Discussion

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Boundary Layer Flow and Heat Transfer with Variable Fluid Properties on a Moving Flat Plate in a Parallel Free Stream

Abstract

1. Introduction

2. Problem Formulation

3. Special Cases

3.1. Constant Fluid Properties (Case A)

3.2. Variable Viscosity (Case B)

4. Results and Discussion

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information