Journal of Applied Mathematics
Volume 2012, Issue 1 364086
Research Article
Open Access

Risk-Control Approach for a Bottleneck Spanning Tree Problem with the Total Network Reliability under Uncertainty

Takashi Hasuike, 

Corresponding Author

Takashi Hasuike

Graduate School of Information Science and Technology, Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan osaka%2Du.ac.jp

Search for more papers by this author
Hideki Katagiri, 

Hideki Katagiri

Graduate School of Engineering, Hiroshima University, 1-4-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8527, Japan hiroshima%2Du.ac.jp

Search for more papers by this author
Hiroshi Tsuda, 

Hiroshi Tsuda

Department of Mathematical Sciences, Faculty of Science and Engineering, Doshisha University, 1-3 Tatara Miyakodani, Kyotanabe, Kyoto 610-0321, Japan doshisha.ac.jp

Search for more papers by this author
First published: 02 October 2012
https://doi.org/10.1155/2012/364086
Citations: 1
Academic Editor: Baocang Ding

Abstract

This paper considers a new risk-control and management approach for a bottleneck spanning tree problem under the situation where edge costs in a given network include randomness and reliability. Particularly, this paper focuses on the case that only mean value and variance of edge costs are calculated without assuming a specific random distribution. In order to develop the risk control approach, a confidence interval-based formulation is introduced. Using this interval, as well as minimizing the maximum value of worse edge costs, maximizing the minimum value of robust parameters to edge costs is introduced as objective functions in the risk-control. Furthermore, in order to maintain the constructing spanning tree network entirely, the reliability for each edge is introduced, and maximizing the total reliability of spanning tree is assumed as the third objective function. The proposed model is a multiobjective programming problem, and hence, it is difficult to solve it directly without setting some optimal criterion. Therefore, satisfaction functions for each object and the integrated function are introduced, and the exact solution algorithm is developed by performing deterministic equivalent transformations. A numerical example is provided by comparing our proposed model with previous standard models.

1. Introduction

Minimum spanning tree (MST) problem is one of most important combinatorial optimization nodes. In the real world, MST problems to find a least cost spanning tree in an edge weighted graph connecting all are usually seen in real-world network optimization problems (most recently, Chen [1] and Ferreira et al. [2]). In more detail, when designing a layout for telecommunication and power networks or constructing a large-scale gas pipeline, if a decision maker wishes to minimize the cost for connection between cities, the situation is formulated as an MST problem. Then, another object is to minimize the working hours for construction or to maximize the reliability to the whole of constructing network. In fact, European Commission [3] today presented its energy infrastructure priorities for the next two decades, aimed at making networks fit for the 21st century. Then, the commission defines EU priority corridors for the transport and networks of electricity, gas, and oil. Thus, it is important to construct several types of networks actually enhancing the importance and the reliability of backbone lines as well as minimizing the cost and constructing time.

In MST problems, there are two main problems whose objects are different from each other. The ordinary object of MST problem is minimizing the total cost of spanning tree, and another is minimizing the maximum value of edge costs in a spanning tree. The latter model is particularly called bottleneck spanning tree (BST) problem, and it is more efficient for the construction of information and communications networks under delivery deadline or capacity constraints of edges. For instance, in the case of constructing new power lines or internet networks among all houses in a town, builders generally construct all lines concurrently, and hence, it is important to construct all lines safely by the delivery deadline. As a mathematical formulation of this case, the BST problem may be appropriate. Therefore, in this paper, we focus on a BST problem.

Previous researches of MST problems including BST problems deal with constant edge costs, and it is possible to apply many exact and polynomial time solution algorithms directly, developed by Cheriton and Tarjan [4], Gabow et al. [5], Geetha and Nair [6], Kruskal [7], and Prim [8]. However, more practically, it is necessary to consider the situation that one makes an optimal decision on the basis of data involving various uncertainties. For instance, the cost to connect between two nodes often depends on the economical environment which varies randomly. In risk-control and management approaches in order to avoid adverse impacts derived from uncertainty, it is recently important to minimize a downside risk which can denote the risk of edge cost going up to some target level set by the decision maker. As a recent study, note the design of a communication network where routing delays on links are not known with certainty due to the time varying nature of the traffic load on the network. In this application, it is desirable to construct a network configuration that hedges against the worst possible contingency in routing delays (Kouvelis and Yu [9]).

If all random distributions to edge costs are certainly determined such as normal distributions, the decision maker may directly use some downside risk measures such as value at risk (VaR) and conditional value at risk (cVaR) (Rockafellar and Uryasev [10]). However, in practice, it is difficult to determine a certain random distribution to each edge cost even if there are a lot of received data. Instead, it is usually possible to calculate mean value and variance derived from received data, and hence, a confidence interval-based approach may be also obtained using only mean value and variance. In general, if the decision maker assumes many practical situations from better to worse cases, this situation mathematically means that the range of confidence interval becomes wide. Therefore, the problem with the confidence interval is regarded as one of robust programming problems. As an extension of the previous confidence interval, Watada et al. [11] recently proposed d-confidence interval where parameter d represents an adjustment parameter to the confidence region in robustness. For instance, in a normal distribution with mean value m and variance σ2, the d-confidence interval is represented as [m − dσ, m + dσ]. In this paper, we propose an MST problem using the d-confidence interval.

On the other hand, it is also important to consider how we ensure the reliability of trunk and backbone line in the network. For instance, we consider that the decision maker constructs a fast Internet network among cities with some important metropolises. In this situation, even if it happens that the only connection between two cites is disrupted by destroying the connection line derived from natural disasters or breakdown of machines, a city loses contact with the other cities and metropolises and this wreaks enormous damages in the whole network. Therefore, it is often important and necessary to construct more reliable lines connecting these metropolises even if the total cost is high. Thus, we need to set the reliability of each edge and to decide the minimum spanning tree maximizing the total reliability to the whole of spanning tree as well as minimizing the total cost.

In mathematical programming under uncertainty, some researchers proposed a stochastic, fuzzy, or uncertain network optimization. As studies of BST problems under uncertainty, Ishii and Nishida [12] and Katagiri et al. [13] investigated BST problems where edge costs are assumed to be random or fuzzy random variables and developed a polynomial-time algorithm. However, risk-control and management models for BST problems with multiobjective functions have not been studied deeply since it is usually formulated as a constrained spanning tree problem which is more difficult to deal with. In this paper, we assume the situation where the decision maker has satisfaction levels for all objects, and hence, we introduce satisfaction functions to objective functions, which are often called fuzzy goals. Furthermore, as an integrated function of multiobjective functions, we focus on the Bellman-Zadeh minimum operator (Bellman and Zadeh [14]) which is one of the standard appropriate aggregation functions and is dealt with in many studies. Using these mathematical formulations, we transform main problems into the deterministic equivalent problems and obtain the exact solution algorithm.

This paper is organized as follows. In Section 2, we introduce a standard BST problem and three objects of our proposed model. Then, we formulate our proposed multiobjective BST problem. In Section 3, in order to solve the proposed BST problem directly in mathematical programming, we introduce satisfaction functions for all objects and Bellman-Zadeh’s minimum operator as an integrated function. In Section 4, performing deterministic equivalent transformations of the initial problem, we develop the polynomial-time solution algorithm based on a standard MST problem and the bisection method. Furthermore, in order to represent some features of our proposed BST problem by comparing with the standard BST problem and probability maximization-based BST problem not including the total reliability, Section 5 provides a simple numerical example. Finally, Section 6 concludes this paper.

2. Mathematical Formulation of Proposed Multiobjective BST Problem

In this section, we introduce a formulation of standard MST problem and our proposed robust MST problem with the reliability to the whole of spanning tree under uncertainty.

We assume a connected undirected graph G = (V, E) where V = {v1, v2, …, vn} is a finite set of n vertices representing terminals or telecommunication stations and so forth. E = {e1, e2, …, em} is a finite set of edges representing connections between these terminals or stations, and T = {T1, T2, …, Tk} is a finite set of spanning trees in given undirected graph G = (V, E). Let undirected graph be a vector defined by
()
where S is the index set of edges.

2.1. Formulation of Standard BST Problem

First, we introduce a standard BST problem. The ordinary MST problem is to find the spanning tree minimizing the total cost. On the other hand, a BST problem is formulated as follows:
()
where cj(j ∈ S) are edge costs in the given undirected graph. The above problem is easily transformed into a minimum spanning tree problem if all edge costs are constant in this problem. Therefore, the efficient solution algorithms are applied to the problem, and it is not difficult to obtain the optimal spanning tree in a polynomial time.

However, we should consider that all edge costs are uncertain values rather than constant in real-world practical situations. In this paper, we assume the case to calculate the mean value and variance of each edge cost using some data but cannot determine a specific random distribution. From mean value and variance of each edge cost, we define a d-confidence interval of each edge cost based on the study (Watada et al. [11]) using parameter dj as where mean values and robust parameters dj are positive. If the random distribution occurs according to a general ellipsoidal distribution such as the normal, Student t, Pareto’s distributions, this formulation denotes the value at risk satisfying with some risk factors. Furthermore, if the random distribution occurs according to the stable distribution such as the normal, Cauchy’s, and Levy’s distributions, this formulation denotes the conditional value at risk (for instance, Rachev et al. [15]). Therefore, we focus on of d-confidence interval and regard parameter dj as the downside risk in robustness.

2.2. Objects for the Proposed Model

  • (i)

     Minimizing the maximum value of downside edge cost .

In practical network optimization and previous standard BST problem (2.2), it is natural for the decision maker to minimize the maximum value of downside edge costs . Therefore, minimizing the maximum value of is also formulated as the following problem:
()
Introducing parameter f as an acceptable target edge cost, the above problem is equivalently transformed into the following problem:
()
  • (ii)

     Maximizing the minimum value of robust parameters dj.

In robustness, if parameter dj is constant and of larger value, interval is also wide. It urges the decision maker to deal with more robust cases than the small value of dj. In risk control and management, it is also important to maximize the minimum value of parameter dj, and hence, the following robust BST problem is formulated:
()
In a way similar to the transformation from problems (2.3) to (2.4), problem (2.5) is also equivalently transformed into the following problem introducing parameter as a target value of robustness:
()
  • (iii)

     Maximizing the total reliability to the whole of spanning tree.

It is also often necessary to construct the network connecting nodes keeping the higher reliability even if the worst value of edge cost is large. This means that we need to set the reliability of each edge and to decide a spanning tree maximizing the total reliability as well as minimizing the maximum value of downside edge costs and maximizing the minimum value of robust parameters. In this paper, we assume that the decision maker gives a constant value of reliability βj to each edge as a constant value from 0 to 1 according to edge costs that is, βj ∈ [0,1].

In this paper, we focus on the concept that the whole of spanning tree is nonfunctional as a normal communication network even if only one edge in the spanning tree is broken down. Therefore, the problem maximizing the total reliability of spanning tree is formulated as the following problem:
()
The objective function of problem is often used in the mathematical formulation maximizing the total reliability in communication networks.

2.3. Main Formulation of Our Proposed BST Model

By integrating these three objects, our proposed BST model is formulated as the following multiobjective programming problem:
()
This problem is a multiobjective programming problem, and hence, it is hard to solve it directly in mathematical programming problem without some optimal criterion. Therefore, in the following sections, we discuss a solution approach to solve problem (2.8) in mathematical programming.

3. Introduction of Fuzzy Goals and Bellman-Zadeh’s Minimum Operator

In multiobjective programming problem (2.8), it is difficult to deal with a tradeoff between the total cost f and robustness parameter directly, because these attributes are completely opposite. Furthermore, taking account of satisfaction of decision maker and robustness for the execution of network, the decision maker often has satisfaction functions for target values of the total cost f, the robust parameter , and the total reliability , which is often called fuzzy goals.

In this paper, we define the following satisfaction function characterized by linear membership functions:
()
where fL, fU, dL, dU, βL, and βU are constant positive values determined by the decision maker. Introducing these satisfaction functions into problem (2.8), we reformulate the proposed BST problem as follows:
()
Problem (3.2) is also a multiobjective programming problem, and hence, it remains the difficulty of solving this problem directly since a complete optimal solution that simultaneously optimizes all of the multiobjective functions does not always exist. Therefore, instead of a complete optimal solution, a Pareto optimal solution may be reasonable for a multiobjective case.

As a reasonable solution concept for the fuzzy multiobjective decision-making problem, a Pareto optimal solution is defined as follows in the ordinary multiobjective programming problem proposed by Sakawa et al. (Sakawa [16], Sakawa et al. [17]):

Definition 3.1. Let x and X be a decision variable column vector and a set of feasible solutions, respectively. Then, x* ∈ X is said to be an M-Pareto optimal solution if and only if there does not exist another x ∈ X such that , and , and either , or .

Introducing an aggregation function μD(x) for three membership functions and , the problem can be rewritten as follows:
()
The aggregation function μD(x) represents the integrated satisfaction or preference degree of the decision maker for the whole of satisfaction functions. Some researchers have proposed aggregation functions: the minimum operator (Bellman and Zadeh [14]), the product operator (Zimmermann [18]), and so forth. Particularly, the following Bellman-Zadeh’s minimum operator ZG is one of the standard appropriate aggregation functions and is dealt with in many studies, and the mathematical formulation is to minimize the aspiration value in all satisfaction functions:
()
Therefore, setting satisfaction functions for the multiobjective and introducing the Bellman-Zadeh minimum operator, we transform problem (3.2) into the following single objective programming problem:
()
In mathematical programming, the optimal solution of problem (3.5) is also the same as that of the following problem introducing parameter h which means the common target satisfaction level:
()

4. Development of Polynomial-Time Solution Algorithm for the Proposed BST Problem

In problem (3.6), the first, second, and third constraints are equivalently transformed into the following inequalities without the loss of optimality.

First constraint:
()
Second constraint:
()
Third constraint:
()
Furthermore, these constraints (4.1), (4.2), and (4.3) are reduced as follows:
()
Consequently, problem (3.6) is equivalently transformed into the following problem:
()
We focus on third constraint in the above problem. In problem (4.5), decision variables xj, (j ∈ S) become only 0 or 1, respectively. Therefore, holds. Using this formula, since and βL + h(βU − βL) are positive, this constraint is equivalently transformed into the following logarithmic constraint without the loss of optimality:
()
Therefore, the optimal solution of problem (4.5) is the same as that of the following problem:
()
Furthermore, by reducing the first and second constraints in problem (4.7) as follow:
()
problem (4.7) is also equivalently transformed into the following problem introducing β(h) = βL + h(βU − βL):
()
This problem is a constrained spanning tree problem. In general, it is difficult to solve constrained network optimization problems in the polynomial time. However, since problem (4.9) fulfills the following theorem, we will show that the solution algorithm of problem (4.9) in the polynomial-time.

Theorem 4.1. Fix parameter , and set . If , then xj = 0, that is, edge ej is not included in the optimal spanning tree.

Proof. Since and , xj < 1 is obtained. Furthermore, since xj is a 0-1 decision variable, xj = 0 is also obtained.

From Theorem 4.1, we can narrow feasible spanning trees in the given network. Furthermore, in the case of fixed parameter , we introduce an auxiliary problem of problem (4.9) as follows:
()
where i is the maximum number of index j satisfying . Since we assume 0 < βj ≤ 1, log βj is a negative value. Therefore, the above problem is equivalently transformed into the following minimizing problem:
()
This auxiliary problem is the same as a standard MST problem, and hence, it is possible to obtain the optimal spanning tree in the polynomial time using the Kruskal algorithm [7] or the Prim algorithm [8]. Furthermore, as an optimality condition between this auxiliary problem and problem (4.9), the following theorem holds.

Theorem 4.2. Let be the optimal solution of auxiliary problem (4.11), and let h* be the optimal value of problem (4.9). Then, the following rules hold:

()

Proof. log β(h) is an increasing function on h due to setting membership function (3.1). Then, since is a decreasing function on h from decreasing function f(h) and increasing function d(h), the number of indexes satisfying xj(h) < 1 is increasing. Therefore, in the case of , the feasible region of problem (4.11) of n the case of is narrower than h, and that is, holds. Consequently, from increasing function log β(h) and decreasing function , this theorem is obtained.

Consequently, from Theorems 4.1 and 4.2 and auxiliary problem (4.9), we develop the following solution algorithm for our proposed BST problem (3.6).

4.1. Solution Algorithm

Step 1. Elicit the satisfaction functions , and by the decision maker, and go to Step 2.

Step 2. Set hL ← 0, hU ← 1, k ← 1, and go to Step 3.

Step 3. In the case h1 = 1, solve problem (4.11). If the optimal spanning tree is obtained, then is also the optimal spanning tree of our proposed model (3.6), and terminate this algorithm. If not, go to Step 4.

Step 4. In the case h1 = 0, solve problem (4.11). If there are no feasible solutions, return to Step 1 and reset parameters of satisfaction functions , and . If not, go to Step 5.

Step 5. Set hk ← (hL + hU)/2, and go to Step 6.

Step 6. Calculate Rj(hk) of each edge ej, and check Rj(hk) ≥ 1 or not. If Rj(hk) < 1, then , and go to Step 7.

Step 7. Solve auxiliary problem (4.11) of the proposed model, and obtain the optimal spanning tree . Then, calculate , and go to Step 8.

Step 8. From Theorem 4.2, if , then is also the optimal solution of our proposed BST problem (3.6), and hence, is the optimal spanning tree. Therefore, terminate the algorithm. Then, in the case k ≥ 2, if , and the following conditions holds:

()
is the optimal spanning tree of the proposed problem (3.6), and terminate this algorithm. If not, go to Step 9.

Step 9. If , then hL ← hk, k ← k + 1 and return to Step 3. If , then hU ← hk, k ← k + 1 and return to Step 5.

Consequently, solving problem (4.11) on each parameter hk using this solution algorithm, we obtain an exact bottleneck spanning tree for our proposed BST problem (3.6) according to decision maker’s satisfaction. The main steps of this solution algorithm is to solve auxiliary problem (4.11) and to do the bisection method on parameter h. The computational complexity to solve auxiliary problem (4.11) are polynomial time due to Kruskal’s or Prim’s polynomial time algorithm. Then, the computational complexity of bisection method is also polynomial time. Therefore, the total computational complexity of this solution algorithm from Steps 1 to 9 is the polynomial-time.

5. Numerical Example

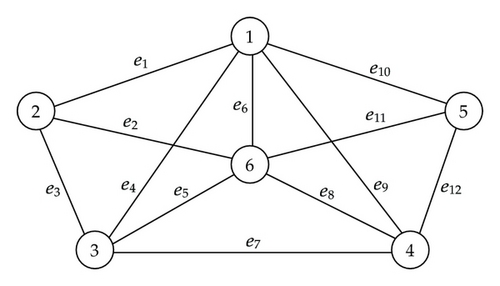
In this section, we provide a simple numerical example. Let G be a graph with 6 vertices that is, n = 6. Figure 1 illustrates the given graph G, and parameters in this example are given in Table 1. In the real world applications such as construction of telecommunication stations networks between cities, some uncertain factors may intervene in the decision making of the construction cost. Furthermore, in the case to ensure the reliability of trunk and backbone networks, we also need to enhance the reliability of spanning tree as well as robustness of edge costs. Therefore, using the numerical example in this section, we compare our proposed BST problem with the standard BST problem and probability maximization-based BST problem not including the reliability.

Table 1. Parameter values of random edge costs with the reliability.
Edge Mean value Variance Reliability
e1 3.0 1.0 0.99
e2 4.0 0.5 0.99
e3 2.0 0.5 0.98
e4 7.0 1.0 0.99
e5 3.5 2.0 0.97
e6 8.0 4.0 1.00
e7 4.0 0.2 0.97
e8 3.0 1.0 0.98
e9 6.0 2.0 0.98
e10 4.0 2.5 0.99
e11 4.5 0.1 0.99
e12 5.0 1.5 0.98
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Given graph G.

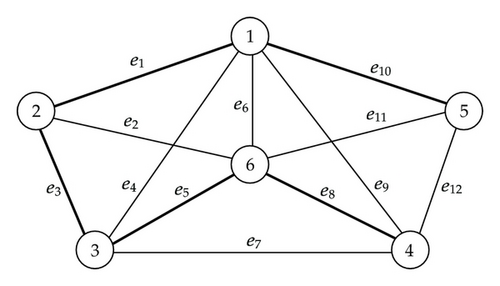
First, we solve a standard BST problem using data of constant edge costs not including the reliability. As constant edge costs, we deal with mean values in Table 1. Using the mean values, we solve the standard BST problem, and obtain the optimal spanning tree as Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Optimal spanning tree of standard BST problem.
Next, we consider the case where each edge cost is a random variable not including the reliability of spanning tree that is, we solve the following probability maximization-based BST problem:
()

We use data of parameters in Table 1, and set parameter f = 5. We solve problem (5.1) and obtain the optimal spanning tree as Figure 3.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Optimal spanning tree of probability maximization-based BST problem.

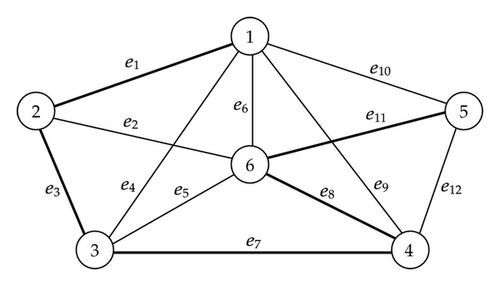
Comparing Figure 3 with Figure 2, edges e5 and e10 selected in Figure 2 are changed into edges e7 and e11. Numerical data in Table 1 shows that mean values of edges e5 and e10 are similar to those of edges e7 and e11, respectively. However, variances of edges e5 and e10 are much higher than those of edges e7 and e11, and hence, probability maximization-based BST problem, which is a subproblem of our proposed BST problem, tends to avoid the uncertain risk derived from variances.

Finally, we solve our proposed BST problem with maximizing the reliability of the whole of spanning tree. We set parameters of satisfaction functions , and as fL = 4, fU = 6, dL = 0.5, dU = 2.0, βL = 0.90, βU = 0.95, respectively. Using data of random edge costs in Table 1, we solve our proposed BST problem according to the solution algorithm in Section 4 and obtain the optimal spanning tree represented in Figure 4.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Optimal spanning tree of our proposed BST problem with the reliability.

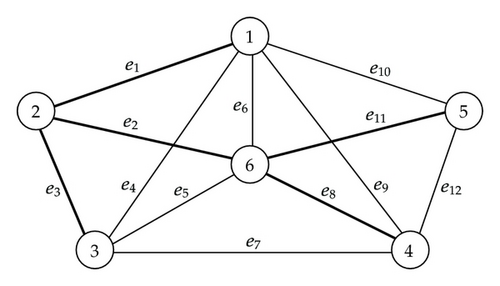
Comparing Figure 4 with Figures 2 and 3, edge e11 is selected in Figure 4 in the same manner as Figure 3, which is not selected in Figure 2. On the other hand, edge e7 selected in Figure 3 is changed into edge e2. This is why the reliability of e7 is smaller than that of edge e2 from Table 1. In our proposed BST problem, we simultaneously consider the higher total reliability of spanning tree, and hence, our proposed model with randomness and the reliability is well balanced between constructing more reliable edges and avoiding uncertain risks.

6. Conclusion

In this paper, we have proposed a new bottleneck spanning tree problem that each edge cost includes both uncertainty derived from randomness and the reliability of given spanning tree and have developed the risk control and management approach. Since it is difficult to determine a specific random distribution to each edge cost from received data, we have considered the d-confidence interval based on only mean value and variance in risk-control and management to avoid adverse impacts derived from uncertainty. Our proposed model has been formulated as a multiobjective bottleneck spanning tree problem such as (i) minimizing the maximum value of worse edge costs, (ii) maximizing the minimum robustness derived from the d-confidence interval of each edge, and (iii) maximizing the reliability to the whole of spanning tree. Furthermore, in order to deal with the satisfaction for the objects of the decision maker and to solve the proposed model in mathematical programming, we have introduced satisfaction functions for all objects and developed the exact solution algorithm using Bellman-Zadeh’s minimum operator and deterministic equivalent transformations. By comparing our proposed model with some existing models of bottleneck spanning tree problems using a numerical example, we have obtained the result that our proposed model with randomness and the reliability was well balanced between constructing more reliable edges and avoiding uncertain risks.

Our modeling approach to introduce robustness and reliability in a given network is simple and has usefulness in well-balanced network between robustness and reliability. Furthermore, our proposed model will be naturally applied to the other network optimization problems such as the shortest path problem and the maximum flow problem. Therefore, this study will be based on the other extended studies of network optimization. In this problem, it is also important to determine the value of the reliability to each edge and the relativity between any two edges strictly, and hence, we are now attacking to construct the exact and mathematical method to determine the reliability and relativity of all edges as a future study.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.