An Underactuated Drift-Free Left Invariant Control System on a Specific Lie Group

Proposition 2.1. The Lie algebra 𝒢 of G is generated by

and the Lie algebra structure of 𝒢 is given by the following

Proposition 2.2. The minus-Lie-Poisson structure on 𝒢^*≃(R⁴) ^*≃R⁴ is generated by the matrix

An easy computation leads one to the following.

Proposition 2.3. The following two systems are drift-free-left invariant controllable systems on G, namely:

where X ∈ G,   A_i are the matrix defined above, and $$.

Proof. Since the span of the set of Lie brackets generated by A₁, A₂, and A₃ coincides with 𝒢 the proposition is a consequence of a result due to Jurdjevic and Sussmann [6].

Proposition 3.1. The controls that minimize J and steer the system (2.5) from X = X₀ at t = 0 to X = X_f at t = t_f are given by

where $$’s are solutions of

Proof. Let us consider the optimal Hamiltonian given by

It is in fact the controlled Hamiltonian H_opt given by which is reduced to 𝒢^* via Poisson reduction. Then the optimal controls are given by where $$’s are solutions of the reduced Hamilton′s equations given by which is nothing else than the required (3.3).

Remark 3.2. It is easy to see from (3.3) that x₄ = constant, and so the dynamics (3.3) can be put in the equivalent form

Proposition 3.3. The dynamics (3.8) has the following Hamilton-Poisson realization:

where and the Hamiltonian

Proof. Indeed, it is not hard to see that the dynamics (3.8) can be put in the equivalent form

as required. Moreover, the function C given by is a Casimir of our configuration. Indeed, as desired.

Remark 3.4. The phase curves of the dynamics (3.8) are intersections of

with see Figure 1.

Proposition 3.5. The dynamics (3.8) has an infinite number of Hamilton-Poisson realizations.

Proof. An easy computation shows us that the triples

where define Hamilton-Poisson realizations of the dynamics (3.8), as required.

Remark 3.6. The above proposition tells us in fact that (3.8) is unchanged, so the trajectories of motion in ℝ³ remain the same when H and C are replaced by linear combinations of H and C with coefficients which form a real matrix with det one.

Proposition 4.1. The equilibrium states $$, are spectrally stable if $$.

Proposition 4.2. The equilibrium states $$ and $$, are spectrally stable for any M ∈ R.

Proposition 4.3. The equilibrium states $$, are nonlinearly stable if $$.

Proof. We will make the proof using energy-Casimir method (see [7]). Let

be the energy-Casimir function, where φ : R → R is a smooth real-valued function defined on R.

Now, the first variation of H_φ is given by

where This equals zero at the equilibrium of interest if and only if The second variation of H_φ is given by Since $$ and if we choose the function φ such that we can conclude that the second variation of H_φ at the equilibrium of interest is positive definite and, thus, $$ are nonlinearly stable.

Proposition 4.4. The equilibrium states $$ and $$ are nonlinearly stable for any M ∈ ℝ^*.

Proposition 4.5. Near $$, $$, the reduced dynamics has, for each sufficiently small value of the reduced energy, at least 1 periodic solution whose period is close to

Proof. Indeed, we have successively the following:

•  

  (i) the restriction of our dynamics (3.8) to the coadjoint orbit

  $$ ()
  gives rise to a classical Hamiltonian system,

•  

  (ii) the matrix of the linear part of the reduced dynamics has purely imaginary roots. More exactly

  $$ ()

•  

  (iii) consider the following:

  $$ ()
  where
  $$ ()

•  

  (iv) the reduced Hamiltonian has a local minimum at the equilibrium state $$ (see the proof of Proposition 4.3).

Then our assertion follows via the Moser-Weinstein theorem with zero eigenvalue; see [8] for details.

Remark 4.6. The existence of the periodical orbits around the equilibrium points e₂ and e₃ remains an open problem, the Moser-Weinstein theorem with zero eigenvalue being inconclusive.

Proposition 5.1. The dynamics (3.8) allows a formulation in terms of Lax pairs.

Proof. Let us take the following:

then, using MATHEMATICA 7.0, we can put the system (3.8) in the equivalent form as desired.

Proposition 5.2. Kahan′s integrator (5.3) has the following properties:

•  

  (i) it is not Poisson preserving;

•  

  (ii) it does not preserve the Casimir C of the Poisson configuration (ℝ³, Π);

•  

  (iii) it does not preserve the Hamiltonian H of the system (3.8).

Proposition 5.3. The Lie-Trotter integrator (5.8) has the following properties:

•  

  (i) it preserves the Poisson structure Π;

•  

  (ii) it preserves the Casimir C of the Poisson configuration (ℝ³, Π);

•  

  (iii) it does not preserve the Hamiltonian H of the system (3.8);

•  

  (iv) its restriction to the coadjoint orbit (𝒪_k, ω_k), where

  $$ ()

and ω_k is the Kirillov-Kostant-Souriau symplectic structure on 𝒪_k, gives rise to a symplectic integrator.

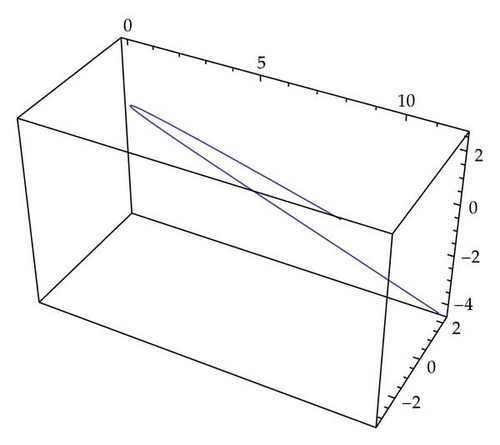
Remark 5.4. If we compare these methods, see Figures 2, 3, and 4, with the 4th-step Runge-Kutta method, we can see that Lie-Trotter integrator and Kahan′s integrator give us a weak approximation of our dynamics. However, Kahan′s integrator and the Lie-Trotter integrator have the advantage of being more easily implemented.