Hopf Bifurcation in an SEIDQV Worm Propagation Model with Quarantine Strategy
Abstract
Worms exploiting zero-day vulnerabilities have drawn significant attention owing to their enormous threats to the Internet. In general, users may immunize their computers with countermeasures in exposed and infectious state, which may take a period of time. Through theoretical analysis, time delay may lead to Hopf bifurcation phenomenon so that the worm propagation system will be unstable and uncontrollable. In view of the above factors, a quarantine strategy is thus proposed in the study. In real network, unknown worms and worm variants may lead to great risks, which misuse detection system fails to detect. However, anomaly detection is of help in detecting these kinds of worm. Consequently, our proposed quarantine strategy is built on the basis of anomaly intrusion detection system. Numerical experiments show that the quarantine strategy can diminish the infectious hosts sharply. In addition, the threshold τ0 is much larger after using our quarantine strategy, which implies that people have more time to remove worms so that the system is easier to be stable and controllable without Hopf bifurcation. Finally, simulation results match numerical ones well, which fully supports our analysis.
1. Introduction
In recent years, with the rapid development of computer technologies and network applications, Internet has become a powerful mechanism for propagating malicious software programs.Systems running on network computers become more vulnerable to digital threats. In particular,worms that exploit zero-day vulnerabilities have brought severe threats to Internet security. To a certain extent, the propagation of worms in a system of interacting computers could be compared with infectious diseases in a population. Anderson and May discussed the spreading nature of biological viruses, parasites and so forth.leading to infectious diseases in human population through several epidemic models [1, 2]. The action of worms throughout a network can be studied by using epidemiological models for disease propagation [3–8]. Mishra and Saini [4] present a SEIRS model with latent and temporary immune periods, which can reveal common worm propagation. Dong et al. propose a computer virus model with time delay based on an SEIR model and regard time delay as bifurcating parameter to study the dynamical behaviors which include local asymptotical stability and local Hopf bifurcation [9]. Ren et al. give a novel computer virus propagation model and study its dynamic behaviors [10]. L.-X. Yang and X. Yang also investigates the propagation behavior of virus programs provided infected computers are connected to the Internet with positive probability [11]. Gan et al. examine the propagation behavior of computer virus under human intervention [12]. The use of a quarantine strategy has produced a tremendous effect on controlling disease. Inspired by this, quarantine strategy is also widely used in worm containment [13–18]. Based on the two-factor model, Zou et al. proposes a worm propagation model under dynamic quarantine defense [15]. Wang et al. proposes a novel epidemic model, which combines both vaccinations and dynamic quarantine methods, referred to as SEIQV model [18].
However, previous studies have failed to consider the appropriate quarantine strategy to eliminate the negative effect of time delay, which may lead to Hopf bifurcation phenomenon so that the worm propagation system will be unstable and uncontrollable. In this paper, time delay is introduced in a worm propagation model. Users may immunize their computers with countermeasures in exposed and infectious state, which may take a period of time. Through theoretical analysis, it is proved that the system is stable when time delay is less than the threshold τ0 and Hopf bifurcation appears when time delay is equal to or greater than the threshold. Moreover, unknown worms and worm-variants may lead to great risks. In order to make up the deficiency of vaccination strategy and eliminate the negative effect of time delay, a quarantine strategy is thus proposed in our study. The current quarantine strategy generally depends on the intrusion detection system, which can be classified into two categories: misuse and anomaly intrusion detection. While misuse detection system fails to detect unknown worms and worm-variants, anomaly detection is of help in detecting these kinds of worm. Consequently, our proposed quarantine strategy is on the basis of anomaly intrusion detection system. According to the above descriptions, we present an SEIDQV worm propagation model to study the behaviors of worm propagation in the real world. Then, the stability of the positive equilibrium and the critical value of Hopf bifurcation are studied. By analysis, the quarantine strategy can diminish the infectious hosts sharply. Moreover, the threshold τ0 is much larger after using our quarantine strategy, which implies that people have more time to remove worms so that the system is easier to be stable and controllable without Hopf bifurcation.
The rest of the paper is organized as follows. Section 2 provides an SEIDQV worm propagation model. In Section 3, we analyze the stability of the positive equilibrium and the threshold of Hopf bifurcation. Section 4 describes the numerical analysis of our model. In Section 5, we present simulation experiments based on slammer worm. The simulation results match well with numerical ones. Finally, Section 6 gives the conclusions.
2. Model Formulation
Considering worms exploiting zero-day vulnerabilities, none of effective and reliable safety patches could immunize the hosts.Susceptible hosts first go through a latent period (exposed) after infection before becoming infectious [9]. People may immunize their computers with countermeasures in exposed and infectious hosts, which may take a period of time. Since time delay exists, infectious hosts go through a temporary state (delayed) after vaccination before becoming vaccinated. What is more, unknown worms and worm-variants may lead to great risks. To our knowledge, quarantine strategies have produced a tremendous effect on controlling disease. Enlightened by this, quarantine strategies are also widely used in worm containment. In order to make up the deficiency of vaccination strategy and eliminate the negative effect of time delay, a quarantine strategy is thus proposed in the study. The current quarantine strategy generally depends on the intrusion detection system, which can be classified into two categories: misuse and anomaly intrusion detection. On one hand, misuse intrusion detection system, which constructs a database with the feather of known attack behaviors, can recognize invaders once their behaviors agree with one of the databases. Although the system can accurately detect known worms, it fails to detect unknown worms and worm variants. On the other hand, an attack can be detected by the anomaly detection system as long as its behavior differs from any database consisting of normal behaviors, which is of help in detecting unknown worms and worm variants. Consequently, our proposed quarantine strategy is on the basis of anomaly intrusion detection system. Meanwhile, anomaly detection system is accompanied by false-positive rates. The quarantine is implemented as follows: the infectious, exposed and susceptible hosts are detected by the anomaly intrusion detection system. The advantage of this strategy lies in detecting unknown worms and worm variants effectively. As anomaly detection system is accompanied by false-positive rates, the quarantine strategy adds two transitions as a result of the influence of the anomaly detection method. The false-positive rates of exposed and susceptible hosts detected by the anomaly detection method are set θ2 and θ3, respectively.
According to the descriptions above, we give an SEIDQV worm propagation model with quarantine strategy. Assume all hosts are in one of six states: Susceptible state (S), Exposed state (E), Infectious state (I), Delayed state (D), Quarantined state (Q), and Vaccinated state (V). Let S(t) denote the number of susceptible hosts at time t, E(t) denote the number of exposed hosts at time t, I(t) denote the number of infectious hosts at time t, D(t) denote the number of delayed hosts at time t, Q(t) denote the number of quarantined hosts at time t, and V(t) denote the number of vaccinated hosts at time t. β is the infection rate at which susceptible hosts are infected by infectious hosts, and γ is the rate of removal of infectious for circulation. μ is the rate that vaccinated hosts become susceptible. Time delay is denoted by τ. More parameters are listed in Table 1. The states and state transition diagram of the SEIDQV model are given in Figure 1.
| Notation | Explanation |
|---|---|
| N | Total number of hosts in the network |
| S(t) | Number of susceptible hosts at time t |
| E(t) | Number of exposed hosts at time t |
| I(t) | Number of infectious hosts at time t |
| D(t) | Number of delayed hosts at time t |
| Q(t) | Number of quarantined hosts at time t |
| V(t) | Number of vaccinated hosts at time t |
| β | Infection rate |
| α | The rate at which exposed hosts become infectious |
| γ | Removal rate of infectious hosts |
| μ | The rate at which vaccinated hosts become susceptible |
| ν | The rate at which exposed hosts are vaccinated or treated |
| δ | Removal rate of quarantined hosts |
| θ1 θ2 θ3 | Quarantine rate of infectious, exposed, and susceptible hosts |
| τ | Time delay of detecting and removing worms |
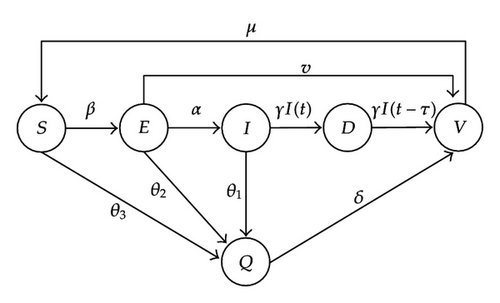
In order to understand clearly, we list in Table 1 some frequently used notations in this paper.
3. Stability of the Positive Equilibrium and Bifurcation Analysis
Theorem 3.1. The system has a unique positive equilibrium E*(S*, E*, I*, D*, Q*, V*) when it satisfies the following condition:
Proof. For system (2.1), if all the derivatives on the left of equal sign of the system are set to 0, which implies that the system becomes stable, we can derive
Obviously, if (H1) is satisfied, (3.3) has one unique positive root I*, and there is one unique positive equilibrium E*(S*, E*, I*, D*, Q*, V*) of system (2.1). The proof is completed.
Theorem 3.2. The positive equilibrium E* is locally asymptotically stable without time delay, if the following holds:
Proof. If τ = 0, (3.6) reduces to
According to Routh-Hurwitz criterion, all the roots of (3.9) have negative real parts. Therefore, it can be deduced that the positive equilibrium E* is locally asymptotically stable without time delay. The proof is completed.
Lemma 3.3. For the polynomial equation (3.13)
Lemma 3.4. Suppose that (H2) p4 + q4 > 0, d1 > 0, (p2 + q2)d1 − (p1 + q1)(p4 + q4) 2 > 0, p1 + q1 > 0 is satisfied.
- (1)
If one of following holds: (a) D0 < 0; (b) D0 ≥ 0, Δ ≥ 0, z1 > 0 and h(z1) < 0; (c) D0 ≥ 0, Δ < 0, and there exists at least z* ∈ (z1, z2, z3) such that z* > 0 and h(z*) ≤ 0, then all roots of (3.6) have negative real parts when τ ∈ [0, τ0), τ0 is a certain positive constant.
- (2)
If the conditions (a)–(c) are not satisfied, then all roots of (3.6) have negative real parts for all τ ≥ 0.
Proof. When τ = 0, (3.6) can be reduced to
By the Routh-Hurwitz criterion,all roots of (3.9) have negative real parts and only if p4 + q4 > 0, d1 > 0, (p2 + q2)d1 − (p1 + q1)(p4 + q4) 2 > 0, p1 + q1 > 0.
From Lemma 3.3, it can be known that if (a)–(c) are not satisfied, then (3.6) has no roots with zero real part for all τ ≥ 0; if one of (a)–(c) holds, when , (3.6) has no roots with zero real part and τ0 is the minimum value of τ, so (3.6) has purely imaginary roots. According to [20], one obtains the conclusion of the lemma.
When conditions (a)–(c) of Lemma 3.4 are not satisfied, h(z) always has no positive root. Therefore, under these conditions, (3.6) has no purely imaginary roots for any τ > 0, which implies that the positive equilibrium E*(S*, E*, I*, D*, Q*, V*) of system (2.1) is absolutely stable. Therefore, the following theorem on the stability of positive equilibrium E*(S*, E*, I*, D*, Q*, V*) can be easily obtained.
Theorem 3.5. Assume that (H1) and (H2) are satisfied, (a) D0 ≥ 0, Δ ≥ 0, z1 < 0 or h(z1) > 0; (b) D0 ≥ 0, Δ < 0, and there is no z* ∈ (z1, z2, z3), such that z* > 0 and h(z*) ≤ 0. Then the positive equilibrium E*(S*, E*, I*, D*, Q*, V*) of system (2.1) is absolutely stable. Namely, E*(S*, E*, I*, D*, Q*, V*) is asymptotically stable for any time delay τ ≥ 0.
Assume that the coefficients in h(z) satisfy the condition as follows:
(H3) (a) D0 ≥ 0, Δ ≥ 0, z1 < 0or h(z1) > 0; (b) D0 ≥ 0, Δ < 0, and there is no z* ∈ (z1, z2, z3), such that z* > 0 and h(z*) ≤ 0.
According to the previous lemma,it is proved that (3.13) has at least a positive root ω0, namely, the characteristic equation (3.6) has a pair of purely imaginary roots ±iω0.
Lemma 3.6. Suppose h′(z0) ≠ 0. If τ = τ0, then ±iω0 is a pair of purely imaginary roots of (3.6). In addition, if the conditions in Lemma 3.4(1) are satisfied, then
Theorem 3.7. Suppose that the conditions (H1) and (H2) are satisfied.
- (1)
The equilibrium E*(S*, E*, I*, D*, Q*, V*) is locally asymptotically stable when τ ∈ [0, τ0), but unstable when τ > τ0.
- (2)
If condition (H3) is satisfied, the system will undergo a Hopf bifurcation at the positive equilibrium E*(S*, E*, I*, D*, Q*, V*) when τ = τk (k = 0,1, 2, …) where τk is defined by (3.16).
This implies that when time delay τ < τ0, the system will stabilize at its infection equilibrium point, which is beneficial for us to implement a containment strategy; when time delay τ > τ0, the system will be unstable and worms cannot be effectively controlled.
4. Numerical Analysis
In order to simulate the real behavior of the spread of a worm, the parameters in the experiments are practical values. The slammer worm is selected for experiments. 750,000 hosts are picked as the population size, and the worm’s average scan rate is 3300 per second. The worm infection rate can be calculated as α = ηN/232 = 0.5763. It means that average 0.5763 hosts of all the hosts can be scanned by one host. The infection rate is β = 3300/232 = 0.00000077, the recovery rate of infectious hosts is set γ = 0.19, the quarantine rates of infectious, exposed and susceptible hosts are set θ1 = 0.15, θ2 = 0.0002, θ3 = 0.00002315. Other parameters are set μ = 0.031, α = 0.45, ν = 0.0001, and δ = 0.04. At the beginning, there are 50 infectious hosts, while others are susceptible. Figures 2–5 show that the propagation trend of the five kinds of host and comparison of infectious hosts before and after adopting quarantine strategy when τ < τ0 and τ > τ0.
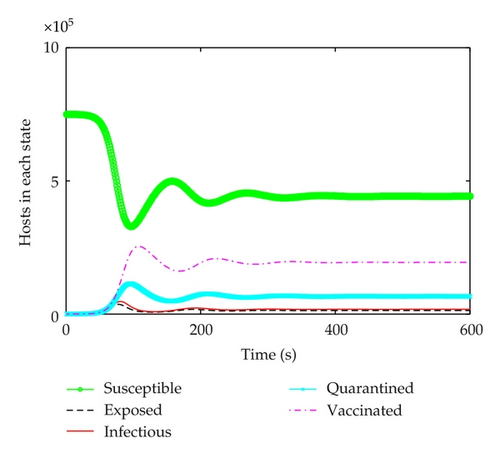

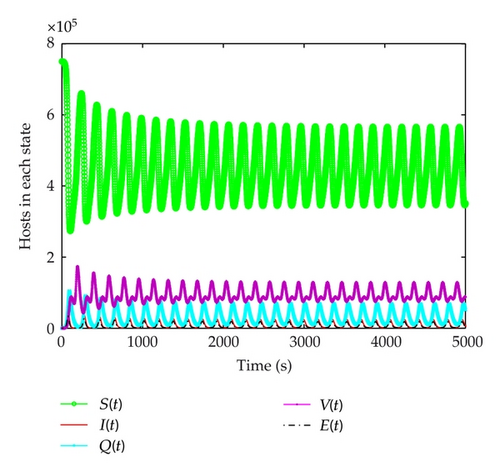
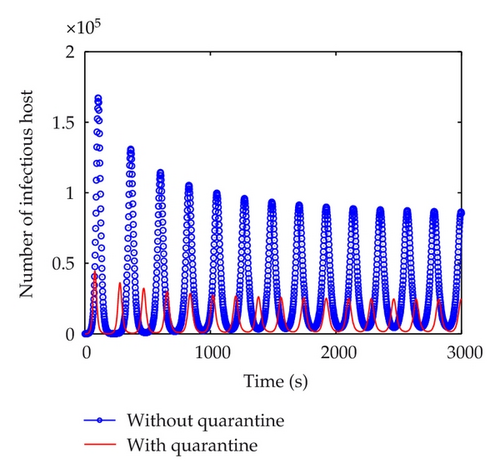
According to the above parameters, Figure 2 shows the curves of five kinds of hosts when τ = 5 < τ0. All of the five kinds of hosts get stable quickly, which illustrates that E* is asymptotically stable. It implies that the number of infectious hosts maintain a relatively low value and can be predicted. Further strategies can be developed and utilized to eliminate worms. In Figure 3, when τ = 5 < τ0, the maximum of infectious hosts is diminished sharply. Finally, the number of infectious hosts is almost 18,000. It is much less than ones without using quarantine strategy. However, when time delay τ gets increased and then reached the threshold τ0, E* will lose its stability and a bifurcation will occur. Figure 4 shows the susceptible, exposed, infectious, quarantined, and vaccinated hosts when τ = 100 > τ0. In this figure, we can clearly see that the number of infectious hosts will outburst after a short period of peace and repeat again and again but not in the same period, which is hard for us to predict the worm spread or eliminate worms. In Figure 5, when τ = 100 > τ0, it is clearly that the maximum of infectious hosts is diminished sharply from 170,000 to 40,000, which illustrates that quarantine strategy has much better inhibition impact than single vaccination.
In order to see the influence of time delay, τ is set to a different value each time with other parameters remaining the same. Figure 6 shows the number of infectious hosts in the same coordinate with time delay τ = 5, τ = 25, τ = 75, and τ = 100.
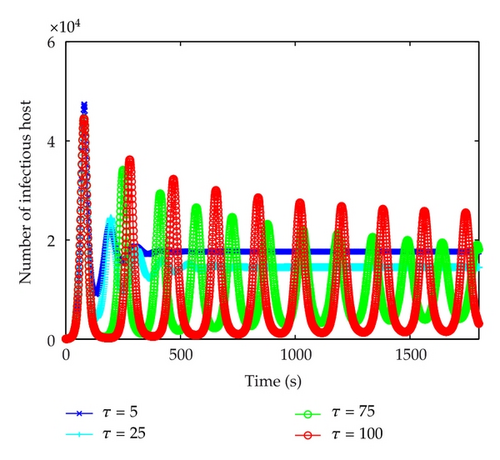
Initially, the four curves are overlapped which means that time delay has little effect in the initial stage of worm propagation. With the increase of time delay, the curve begins to oscillate. When time delay passes through the threshold τ0, the infecting process gets unstable. Meanwhile, it can be discovered that the amplitude and period of the number infectious hosts increase.
Figure 7 shows the projection of the phase portrait of system (2.1) in (S, I, V)-space when τ = 65, τ = 80, respectively. In Figure 8, when τ = 65, it is clear that the curve converges to a fixed point, which suggests that the system is stable. When τ = 80, the curve converges to a limit circle, which implies that the system is unstable.
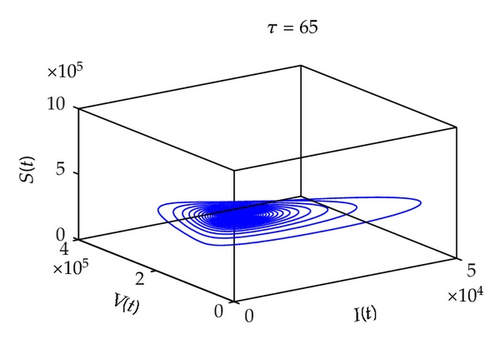
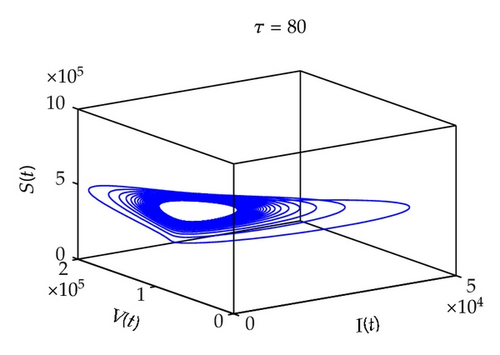
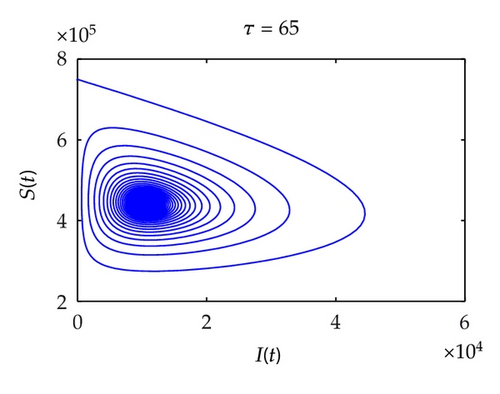
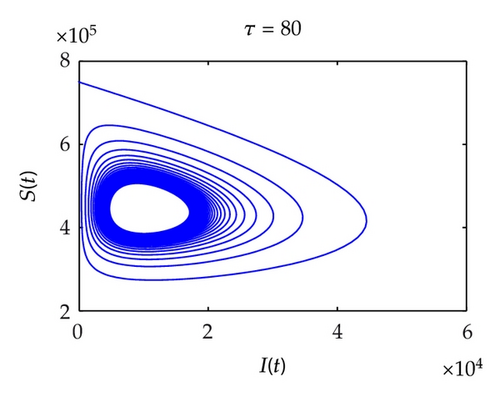
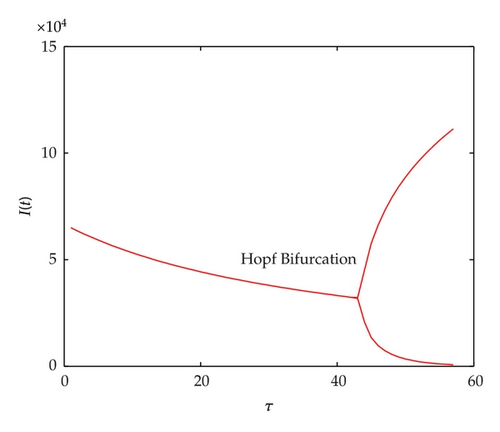
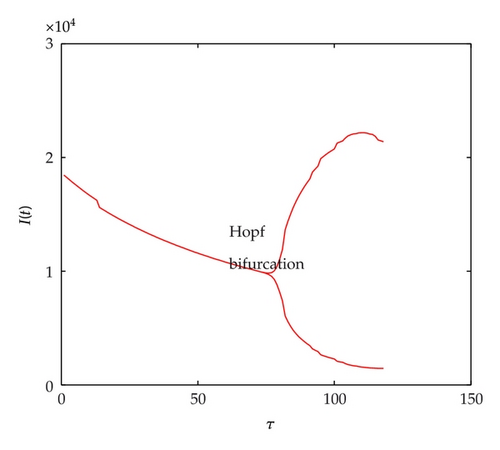
Figure 9 shows bifurcation diagram with τ from 1 to 60; Hopf bifurcation will occur when τ = τ0 = 42. In Figure 10, it shows bifurcation diagram with τ from 1 to 120; Hopf bifurcation will occur when τ = τ0 = 74. The threshold is greater than model without quarantine strategy, which illustrates that the model gets stable easier and the users have more time to remove worms.
5. Simulation Experiments
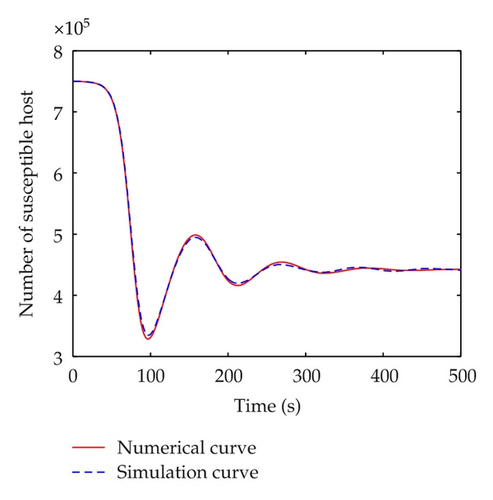
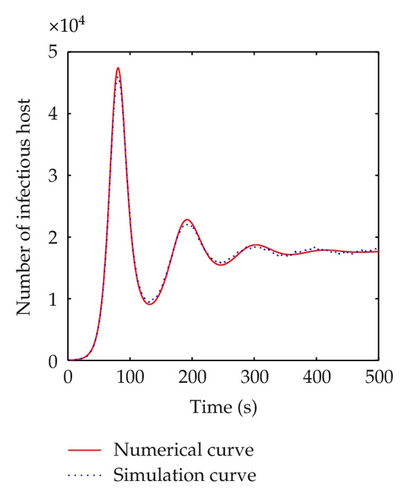
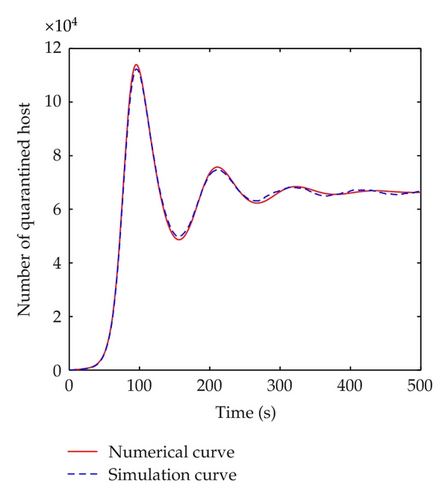
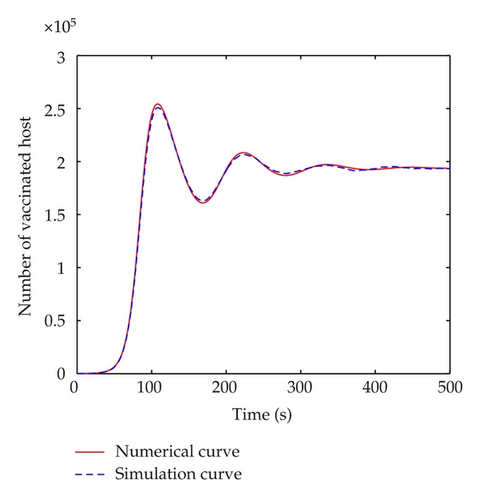
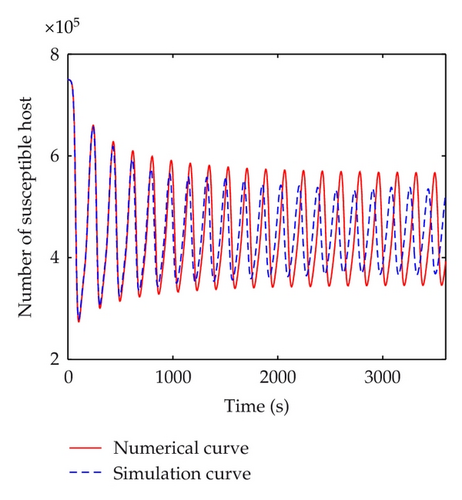
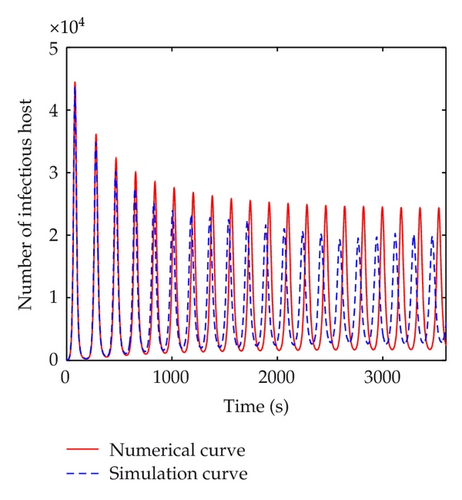
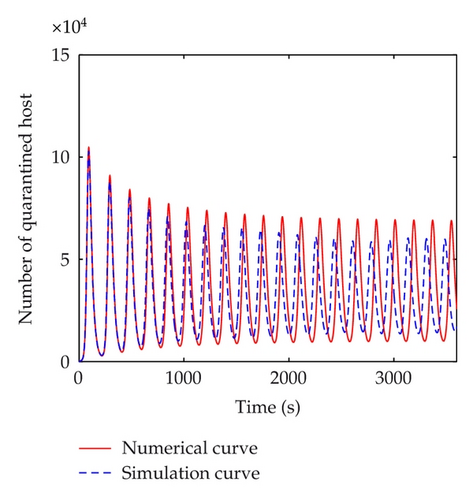
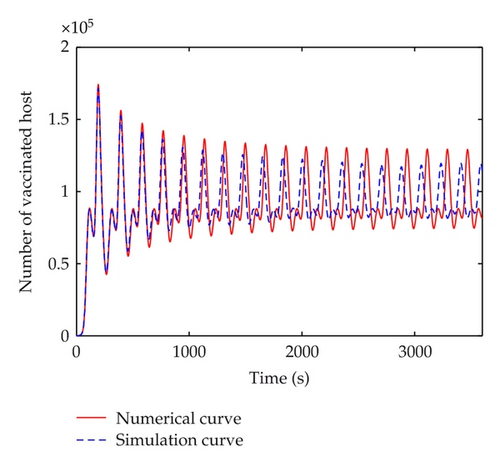
The discrete-time simulation is an expanded version of Zou’s program simulating Code Red worm propagation. The system in our simulation experiment consists of 750,000 hosts that can reach each other directly, which is consistent with the numerical experiments. At the beginning of simulation, 50 hosts are randomly chosen to be infectious and the others are all susceptible. In the simulation experiments, the implement of transition rates of the model is based on probability. Under the propagation parameters of the slammer worm, several simulation experiments are carried out. Figure 11 shows the comparisons between numerical and simulation curves of susceptible, infectious, quarantined and vaccinated hosts respectively, when τ = 5 < τ0, which indicate that the simulation curves match the numerical ones very well. When time delay passes the threshold, a bifurcation appears. Figure 12 shows the difference between simulation and numerical results of the four kinds of host when τ = 100 > τ0. In this figure, the periods of these two curves are well matched. But there is a difference in amplitudes. This mainly results from the precision of experiments. The number of hosts in numerical experiments can be either integers or decimals. However, in simulation experiments, the number of hosts must be integer. In addition, when the number of infectious hosts is very little, the tiny difference may result in a big gap.
6. Conclusions
- (i)
The critical time delay τ0 where Hopf bifurcation appears is obtained
(6.1) - (ii)
When time delay τ < τ0, the worm propagation system will stabilize at its infection equilibrium point, which is beneficial for us to implement a containment strategy to eliminate the worm completely.
- (iii)
When time delay τ ≥ τ0, Hopf bifurcation appears, which implies the system will be unstable and the worm cannot be effectively controlled.
- (iv)
The quarantine strategy can diminish the infectious hosts sharply. The threshold τ0 is much larger after using the proposed quarantine strategy, which implies that people have more time to remove worms so that the system is easier to be stable and controllable without Hopf bifurcation.
In order to control and predict the worm propagation, time delay τ should remain less than the threshold τ0 by decreasing the time of detecting and removing worm. In real world, various factors can affect worm propagation. The paper focuses on analyzing the influence of time delay. Other impact factors to worm propagation will be a major emphasis of our future research.
Acknowledgments
This paper is supported by the National Natural Science Foundation of China under NSFC no. 60803132 and by the Fundamental Research Funds of the Central Universities under no. N100404001.




