Discrete Dynamics in Nature and Society
Volume 2012, Issue 1 282908
Research Article
Open Access

Hopf Bifurcation of a Predator-Prey System with Delays and Stage Structure for the Prey

Zizhen Zhang, 

Zizhen Zhang

Key Laboratory of Advanced Process Control for Light Industry of Ministry of Education, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu 233030, China aufe.edu.cn

Search for more papers by this author
Huizhong Yang, 

Corresponding Author

Huizhong Yang

Key Laboratory of Advanced Process Control for Light Industry of Ministry of Education, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author
First published: 13 December 2012
https://doi.org/10.1155/2012/282908
Citations: 4
Academic Editor: M. De la Sen

Abstract

This paper is concerned with a Holling type III predator-prey system with stage structure for the prey population and two time delays. The main result is given in terms of local stability and bifurcation. By choosing the time delay as a bifurcation parameter, sufficient conditions for the local stability of the positive equilibrium and the existence of periodic solutions via Hopf bifurcation with respect to both delays are obtained. In particular, explicit formulas that can determine the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions are established by using the normal form method and center manifold theorem. Finally, numerical simulations supporting the theoretical analysis are also included.

1. Introduction

Predator-prey dynamics continues to draw interest from both applied mathematicians and ecologists due to its universal existence and importance. Many kinds of predator-prey models have been studied extensively [1–6]. It is well known that there are many species whose individual members have a life history that takes them through immature stage and mature stage. To analyze the effect of a stage structure for the predator or the prey on the dynamics of a predator-prey system, many scholars have investigated predator-prey systems with stage structure in the last two decades [7–15]. In [7], Wang considered the following predator-prey system with stage structure for the predator and obtained the sufficient conditions for the global stability of a coexistence equilibrium of the system:
(1.1)
where x(t) represents the density of the prey at time t. y1(t) and y2(t) represent the densities of the immature predator and the mature predator at time t, respectively. For the meanings of all the parameters in system (1.1), one can refer to [7]. Considering the gestation time of the mature predator, Xu [8] incorporated the time delay due to the gestation of the mature predator into system (1.1) and considered the effect of the time delay on the dynamics of system (1.1).
There has also been a significant body of work on the predator-prey system with stage structure for the prey. In [12], Xu considered a delayed predator-prey system with a stage structure for the prey:
(1.2)
where x1(t) and x2(t) denote the population densities of the immature prey and the mature prey at time t, respectively. y(t) denotes the population density of the predator at time t. All the parameters in system (1.2) are assumed positive. a is the birth rate of the immature prey. b is the transformation rate from immature individual to mature individuals. b1 is the intraspecific competition coefficient of the mature prey. r1 and r2 are the death rates of the immature and the mature prey, respectively. r is the death rate of the predator. a1 and a2 are the interspecific interaction coefficients between the mature prey and the predator, respectively. a1x2/(1 + mx2) is the response function of the predator. And τ is a constant delay due to the gestation of the predator. In [12], Xu investigated the persistence of system (1.2) by means of the persistence theory on infinite dimensional systems, and sufficient conditions are obtained for the global stability of nonnegative equilibrium of the model by constructing appropriate Lyapunov function. But studies on the predator-prey system not only involve the persistence and stability, but also involve many other behaviors such as periodic phenomenon, attractivity, and bifurcation [16–19]. In particular, the properties of periodic solutions are of great interest [20–24]. Therefore, F. Li and H. W. Li [14] considered the property of periodic solutions of the following system:
(1.3)
Motivated by the work of Xu [12] and F. Li and H. W. Li [14] and considering the intraspecific competition of the immature prey population, we consider the following system:
(1.4)
where x1(t) and x2(t) denote the population densities of the immature prey and the mature prey at time t, respectively. y(t) denotes the population density of the predator at time t. The parameters a, a1, a2, b, b1, r, r1, r2, and m are defined as in system (1.3). c is the intraspecific competition of the immature prey, τ1is the feedback delay of the mature prey, and τ2 is the time delay due to the gestation of the predator.

The organization of this paper is as follows. In Section 2, by analyzing the corresponding characteristic equations, the local stability of the positive equilibrium of system (1.4) is discussed, and the existence of Hopf bifurcation at the positive equilibrium is established. In Section 3, we determine the direction of Hopf bifurcation and the stability of bifurcating periodic solutions by using the normal form theory and center manifold theorem in [20]. And numerical simulations are carried out in Section 4 to illustrate the main theoretical results. Finally, main conclusions are included.

2. Local Stability and Hopf Bifurcation

From the viewpoint of biology, we are only interested in the positive equilibrium of system (1.4). It is not difficult to verify that system (1.4) has a positive equilibrium , where
(2.1)
if the following conditions hold: H1 : a2 > mr, .
Let , , y(t) = z3(t) + y0, and we still denote z1(t), z2(t), and z3(t) by x1(t), x2(t), and y(t). Then system (1.4) can be transformed to the following form:
(2.2)
where
(2.3)
Then we can get the linearized system of system (2.2)
(2.4)
Therefore, the corresponding characteristic equation of system (2.4) is
(2.5)
where m0 = (α12α21 − α11α22)α33, m1 = α11α22 + α11α33 + α22α33 − α12α21, m2 = −(α11 + α22 + α33), n0 = −α11α33β22, n1 = (α11 + α33)β22, n2 = −β22, p0 = α11α23γ32 + α12α21γ33 − α11α22γ33, p1 = α11γ33 + α22γ33 − α23γ32, p2 = −γ33, q0 = −α11β22γ33, q1 = β22γ33.

Next, we consider the local stability of the positive equilibrium and the Hopf bifurcation of system (1.4) for the different combination of τ1 and τ2.

Case 1. (τ1 = τ2 = 0). The characteristic equation (2.5) becomes

(2.6)
where m12 = m2 + n2 + p2, m11 = m1 + n1 + p1 + q1, m10 = m0 + n0 + p0 + q0.

It is not difficult to verify that m12 > 0 and m10 > 0. Thus, all the roots of (2.6) must have negative real parts, if the following condition holds: H11 : m12m11 > m10. Namely, the positive equilibrium is locally stable in the absence of time delay, if H11 holds.

Case 2. (τ1 > 0, τ2 = 0). On substituting τ2 = 0, (2.5) becomes

(2.7)
where m22 = m2 + p2, m21 = m1 + p1, m20 = m0 + p0, n22 = n2, n21 = n1 + q1, n20 = n0 + q0.

Let λ = iω1(ω1 > 0) be a root of (2.7). Then, we have

(2.8)
Squaring both sides and adding them up, we get the following sixth-degree polynomial equation:
(2.9)
where , , .

Let , then (2.9) becomes

(2.10)
Define
(2.11)
If e20 < 0, it is easy to know that (2.10) has at least one positive root. On the other hand, if e20 ≥ 0, according to Lemma 2.2 in [25], (2.10) has positive roots if and , hold. Therefore, we give the following assumption.

H21: equation (2.10) has at least one positive root.

Without loss of generality, we assume that it has three positive roots which are denoted as v11, v12, and v13. Thus, (2.9) has three positive roots , k = 1,2, 3. The corresponding critical value of time delay is
(2.12)
where A24 = n21 − m22n22, A22 = m20n22 + m22n20 − m21n21, A20 = −m20n20, , , .

Let , k ∈ {1,2, 3}, .

To verify the transversality condition of Hopf bifurcation, differentiating the two sides of (2.7) with respect to τ1, and noticing that λ is a function of τ1, we can obtain
(2.13)
Thus,
(2.14)
Therefore,
(2.15)
From (2.9), we can get
(2.16)
Then, we have
(2.17)
where .

Therefore, if holds. Notice that and have the same sign. Then we have if H22 holds. In conclusion, we have the following results.

Theorem 2.1. Suppose that the conditions H21 and H22 hold. The positive equilibrium E0 of system (1.4) is asymptotically stable for τ1 ∈ [0, τ10) and unstable when τ1 > τ10. Further, system (1.4) undergoes a Hopf bifurcation when τ1 = τ10.

Case 3. (τ2 > 0, τ1 = 0). On substituting τ2 = 0, (2.5) becomes

(2.18)
where m32 = m2 + n2, m31 = m1 + n1, m30 = m0 + n0, p32 = p2, p31 = p1 + q1, p30 = p0 + q0.

Let λ = iω2(ω2 > 0) be a root of (2.18). Then, we get

(2.19)
which follows that
(2.20)
where , , .

Let , then (2.20) becomes

(2.21)
Define
(2.22)
Similar as in case (2), we give the following assumption.

H31: equation (2.21) has at least one positive root.

Without loss of generality, we assume that it has three positive roots denoted by v21, v22, and v23. Thus, (2.20) has three positive roots .

The corresponding critical value of time delay is
(2.23)
where A34 = p31 − m32p32, A32 = m30p32 + m32p30 − m31p31, A30 = −m30p30, , , .

Let , k ∈ {1,2, 3}, .

Similar as in case (1), next, we suppose that the condition holds, where . Then we have . By the above analysis, we have the following results.

Theorem 2.2. Suppose that the conditions H31 and H32 hold. The positive equilibrium E0 of system (1.4) is asymptotically stable for τ2 ∈ [0, τ20) and unstable when τ2 > τ20. Further, system (1.4) undergoes a Hopf bifurcation when τ2 = τ20.

Case 4. (τ1 = τ2 = τ > 0).

For τ1 = τ2 = τ > 0, (2.5) can be rewritten in the following form:

(2.24)
where m42 = m2, m41 = m1, m40 = m0, n42 = n2 + p2, n41 = n1 + p1, n40 = n0 + p0, q41 = q0, q40 = q0.

Multiplying eλτ on both sides of (2.24), it is obvious to get

(2.25)
Let λ = iω(ω > 0) be the root of (2.25). Then, we have
(2.26)
where Δ41 = q41ω − m41ω + ω3, Δ42 = m40 − m42ω2 + q40, Δ43 = q41ω + m41ω − ω3, Δ44 = m40 − m42ω2 − q40, Δ45 = n42ω2 − n40, Δ46 = −n41ω.

It follows that

(2.27)
where A0 = (q40 − m40)n40, A1 = (m41 + q41)n40 − (m40 + q40)n41, A2 = (m40 − q40)n42 + (q41 − m41)n41 − m42n40, A3 = m42n41 − n40 − (m41 + q41)n42, A4 = n41 − m42n42, A5 = n42, , , .

From (2.27), we can get

(2.28)
where , , , , , .

Let ω2 = v3, then (2.28) becomes

(2.29)
Suppose that (2.29) has at least one positive root, and, without loss of generality, we assume that it has six positive roots which are denoted as v31, v32, v33, v34, v35, and v36. Then, (2.28) has six positive roots .

The corresponding critical value of time delay is

(2.30)
Let , k ∈ {1,2, 3,4, 5,6}, .

Next, we verify the transversality condition. Differentiating (2.25) regarding τ and substituting τ = τ0, we get

(2.31)
where
(2.32)
Thus, if the condition (H42) : AC + BD ≠ 0 holds, the transversality condition is satisfied.

Theorem 2.3. Suppose that the conditions H41 and H42 hold. The positive equilibrium E0 of system (1.4) is asymptotically stable for τ ∈ [0, τ0) and unstable when τ > τ0. Further, system (1.4) undergoes a Hopf bifurcation when τ = τ0.

Case 5. (τ1 > 0 and τ2 ∈ [0, τ20)).

We consider (2.5) with τ2 in its stable interval, and τ1 is considered as a parameter.

Let λ = iω1*(ω1* > 0) be the root of (2.5). Then, we have

(2.33)
where
(2.34)
From (2.33), we can get the following transcendental equation:
(2.35)
where , , , c50 = 2m0p0 − 2n0q0, c51 = 2m0p1 + 2n1q0 − 2m1p0 − 2n0q1, c52 = 2m1p1 + 2n2q0 − 2m2p0 − 2m0p2 − 2n1q1, c53 = 2m1p2 + 2n2q1 + 2p0 − 2m2p1, c54 = 2m2p2 − 2p1, c55 = −2p2.

In order to give the main results, we suppose that (2.35) has finite positive root. We denote the positive roots of (2.35) as ω51, ω52 ⋯ ω5k. For every ω5i(i = 1,2, …, k), the corresponding critical value of time delay is

(2.36)
Let , and is the corresponding root of (2.35) with .

In the following, we differentiate the two sides of (2.5) with respect to τ1 to verify the transversality condition.

Taking the derivative of λ with respect to τ1 in (2.5) and substituting , we get

(2.37)
where
(2.38)
Obviously, if the condition H52 : PRQR + PIQI ≠ 0 holds, the transversality condition is satisfied. Through the above analysis, we have the following results.

Theorem 2.4. Suppose that the conditions H51 and H52 hold and τ2 ∈ [0, τ20). The positive equilibrium E0 of system (1.4) is asymptotically stable for and unstable when . Further, system (1.4) undergoes a Hopf bifurcation when .

Case 6. (τ2 > 0 and τ1 ∈ [0, τ10)).

We consider (2.5) with τ1 in its stable interval, and τ2 is considered as a parameter.

Substitute λ = iω2*(ω2* > 0) into (2.5). Then, we get

(2.39)
where , , , c60 = 2m0n0 − 2p0q0, c61 = 2m0n1 + 2p1q0 − 2m1n0 − 2p0q1, c62 = 2m1n1 + 2p2q0 − 2m2n0 − 2m0n2 − 2p1q1, c63 = 2m1n2 + 2p2q1 + 2n0 − 2m2n1, c64 = 2m2n2 − 2n1, c65 = −2n2.

Similar as in case (5), we give the following assumption. H61: (2.39) has finite positive root.

The positive roots of (2.39) are denoted as ω61, ω62,…,ω6k. For every ω6i (i = 1,2, …, k), the corresponding critical value of time delay is

(2.40)
where
(2.41)
(2.42)
(2.43)
(2.44)

Let , and is the corresponding root of (2.39) with .

Then, we suppose that holds. By the general Hopf bifurcation theorem for FDEs in Hale [26], we have the following results.

Theorem 2.5. Suppose that the conditions H61 and H62 hold and τ1 ∈ [0, τ10). The positive equilibrium E0 of system (1.4) is asymptotically stable for and unstable when . Further, system (1.4) undergoes a Hopf bifurcation at when .

3. Direction and Stability of Bifurcated Periodic Solutions

In Section 2, we have obtained the conditions under which a family of periodic solutions bifurcate from the positive equilibrium of system (1.4) when the delay crosses through the critical value. In this section, we will determine the direction of Hopf bifurcation and stability of bifurcating periodic solutions of system (1.4) with respect to τ1 for τ2 ∈ (0, τ20) by using the normal form method and center manifold theorem introduced by Hassard et al. [20]. It is considered that system (1.4) undergoes Hopf bifurcation at . Without loss of generality, we assume that , where .

Let , t = sτ1, x1(sτ1) = z1(s), x2(sτ1) = z2(s), y(sτ1) = z3(s). We still denote s by t. Then, system (1.4) can be transformed into the following system:
(3.1)
where u(t) = (u1(t), u2(t), u3(t)) T ∈ C = C([−1,0], R3) and Lμ : C → R3, F : R × C → R3 are given, respectively, by
(3.2)
where
(3.3)
Hence, by the Riesz representation theorem, there exists a 3 × 3 matrix function η(θ, μ):[−1,0] → R3 whose elements are of bounded variation such that
(3.4)
In fact, we choose
(3.5)
For ϕ ∈ C([−1,0], R3), we define
(3.6)
and
(3.7)
Then, system (3.1) can be transformed into the following operator equation:
(3.8)
For φ ∈ C′([0,1], (R3) *), where (R3) * is the 3-dimensional space of row vectors, we define the adjoint operator A* of A(0):
(3.9)
For ϕ ∈ C([−1,0], R3) and ϕ ∈ C′([0,1], (R3) *), we define a bilinear inner product:
(3.10)
where η(θ) = η(θ, 0).

By the discussion in Section 2, we know that are eigenvalues of A(0). Thus, they are also eigenvalues of A*.

Suppose that is the eigenvector of A(0) corresponding to and is the eigenvector of corresponding to . By direction computation, we can get
(3.11)
Then, from (3.10), we can get
(3.12)
Therefore, we can choose
(3.13)
such that 〈q*, q〉 = 1 and .
In the remainder of this section, following the algorithms given in [20] and using similar computation process in [27], we can get the coefficients that can be used to determine the direction of Hopf bifurcation and the stability of the bifurcating periodic solutions:
(3.14)
(3.15)
with
(3.16)
where E1, E2 can be determined by the following equations, respectively,
(3.17)
with
(3.18)
(3.19)
Then, we can calculate the following values:
(3.20)

Based on the above discussion, we can obtain the following results.

Theorem 3.1. From (3.20) one has

  • (i)

    the direction of the Hopf bifurcation is determined by the sign of δ: if δ > 0(δ < 0), then the Hopf bifurcation is supercritical (subcritical);

  • (ii)

    the stability of bifurcating periodic solutions is determined by the sign of σ: if σ < 0(σ > 0), the bifurcating periodic solutions are stable (unstable);

  • (iii)

    the period of the bifurcating periodic solution is determined by the sign of T: if T > 0(T < 0), the bifurcating periodic solution increases (decreases).

4. Numerical Example

In this section, we give some numerical simulations to verify the theoretical analysis in Sections 2 and 3. Let a = 8, a1 = 4.25, a2 = 3, b = 5, b1 = 1, c = 0.5, m = 2, r = 1, r1 = 1, and r2 = 2. Then, we have the following particular case of system (1.4):
(4.1)
It is not difficult to verify that a2 > mr, , namely, the conditions H1and H2 hold. Therefore, system (4.1) has at least a positive equilibrium. By means of Matlab, we can get that the positive equilibrium of (4.1) is .

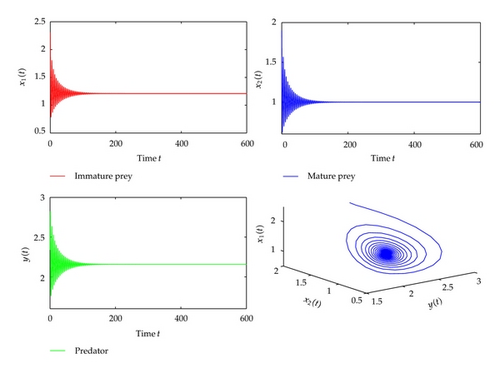
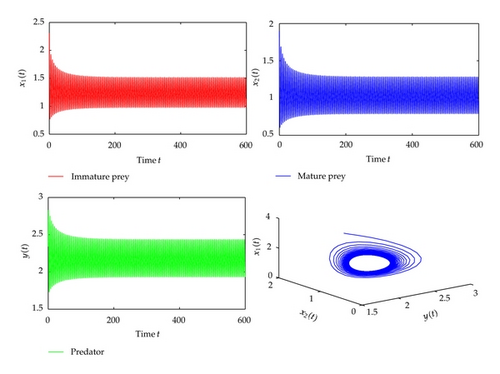
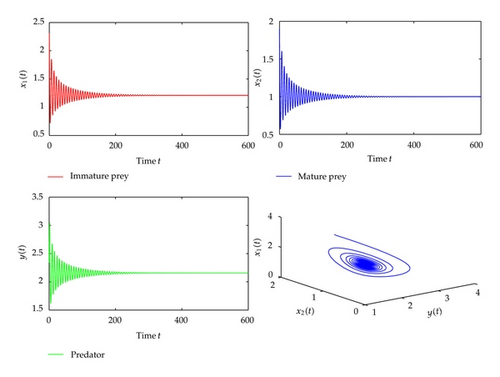
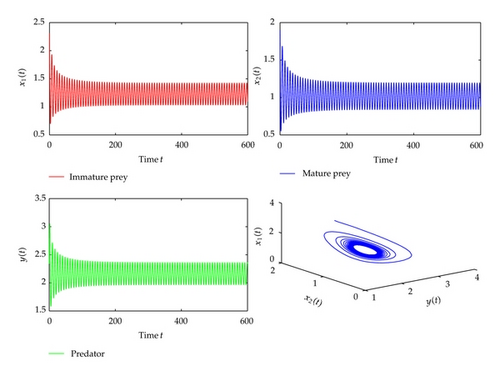
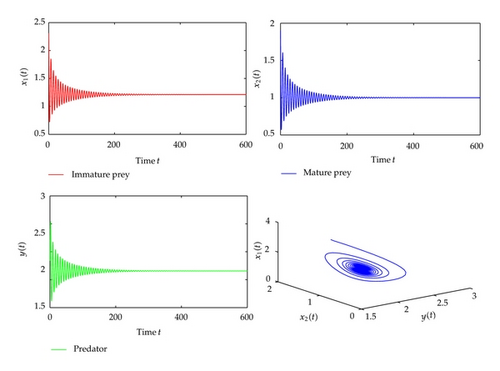
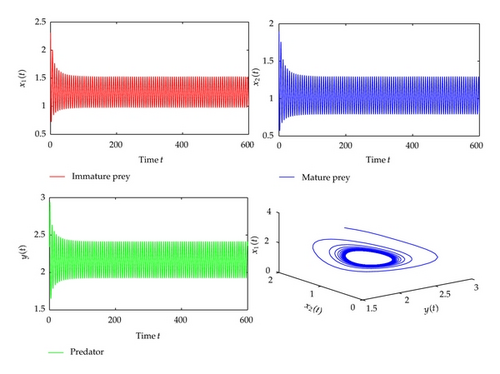
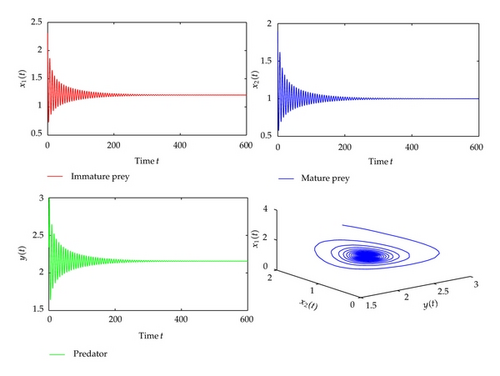
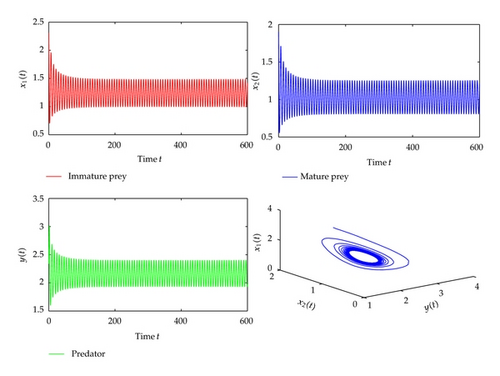
For τ1 > 0, τ2 = 0, we can get ω10 = 1.3881, τ10 = 0.9032. From Theorem 2.2, we know that the positive equilibrium is asymptotically stable when τ1 ∈ [0, τ10). The corresponding waveform and the phase plot are illustrated by Figure 1. When the time delay τ1 passes through the critical value τ10, the positive equilibrium will lose its stability and a Hopf bifurcation occurs, and a family of periodic solutions bifurcate from the positive equilibrium . This property is illustrated by the numerical simulation in Figure 2. Similarly, we have ω20 = 0.8497, τ20 = 0.5124, when τ2 > 0, τ1 = 0. The corresponding waveform and the phase plots are shown in Figures 3 and 4.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
E0 is locally asymptotically stable for τ1 = 0.8500 < τ10 = 0.9032 with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
E0 is unstable for τ1 = 0.9200 > τ10 = 0.9032 with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
E0 is locally asymptotically stable for τ2 = 0.4400 < τ20 = 0.5124 with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
E0 is unstable for τ2 = 0.5500 > τ20 = 0.5124 with initial value “2.31; 1.9; 2.34.”

For τ1 = τ2 = τ > 0, we can obtain ω0 = 1.0000, τ0 = 0.4178. From Theorem 2.2, we know that, when the time delay τ increases from zero to τ0, the positive equilibrium is asymptotically stable. Once the time delay τ passes through the critical value τ0, the positive equilibrium will lose its stability and a Hopf bifurcation occurs. This property is illustrated by the numerical simulation in Figures 5 and 6.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
E0 is locally asymptotically stable for τ = 0.3900 < τ0 = 0.4178 with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
E0 is unstable for τ = 0.4600 > τ0 = 0.4178 with initial value “2.31; 1.9; 2.34.”

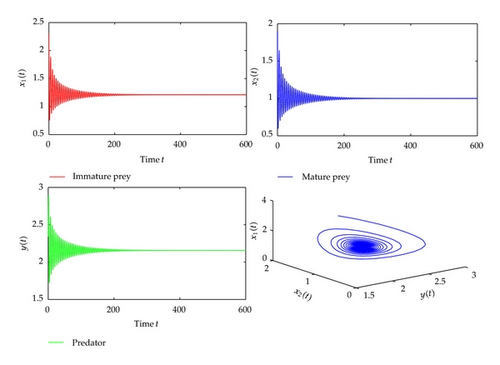
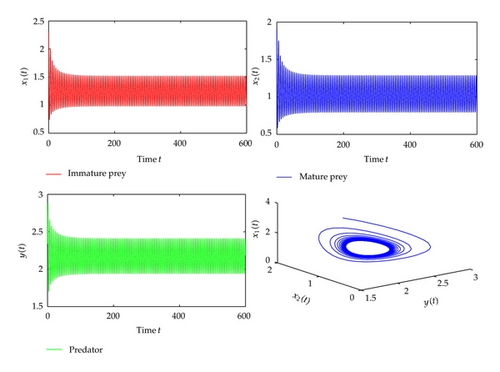
For τ1 > 0 and , we have , . According to Theorem 2.2, the positive equilibrium is asymptotically stable when and unstable when , which can be depicted by the numerical simulation in Figures 7 and 8. In addition, from (3.20), we can obtain C1(0) = −1.1949 + 3.2464i, δ = −23.4294, σ = −2.3898, T = 2.4949. Thus, from Theorem 2.3, we know that the Hopf bifurcation with respect to τ1 with is subcritical, the bifurcating periodic solutions are stable and increase. Similarly, we have , , for τ2 > 0 and . The corresponding waveform and the phase plots are shown in Figures 9 and 10.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
E0 is locally asymptotically stable for and with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
E0 is unstable for and with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
E0 is locally asymptotically stable for and with initial value “2.31; 1.9; 2.34.”
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
E0 is unstable for and with initial value “2.31; 1.9; 2.34.”

5. Conclusions

In this paper, a delayed predator-prey system with Holling type III functional response and stage structure for the prey population is investigated. Compared with literature [14], we consider not only the time delay due to the gestation of the predator but also the negative feedback of the mature prey density and the intraspecific competition of the immature prey population. F. Li and H. W. Li [14] has obtained that the species in system (4.1) with only the time delay due to the gestation of the predator could coexist. However, we get that the species could also coexist with some available time delays of the mature prey and the predator. This is valuable from the view of ecology.

The sufficient conditions for the local stability of the positive equilibrium and the existence of local Hopf bifurcation for the possible combinations of two delays are obtained. The main results are given in Theorems 2.1–2.5. By computation, we find that the time delay due to the gestation of the predator is marked because the critical value of τ2 is smaller than that of τ1 when we only consider them, respectively. Furthermore, the explicit formulae which determines the direction of the bifurcation and the stability of the bifurcating periodic solutions is established when τ > 0 and τ2 ∈ [0, τ20) by using the normal form theory and center manifold theorem. The main results are given in Theorem 2.3. Finally, numerical simulations are carried out to support the obtained theoretical results.

Acknowledgments

The authors are grateful to the anonymous reviewers for their helpful comments and valuable suggestions on improving the paper. This work was supported by the National Natural Science Foundation of China (61273070), Doctor Candidate Foundation of Jiangnan University (JUDCF12030) and Anhui Provincial Natural Science Foundation under Grant no. 1208085QA11.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.