Improving Results on Convergence of AOR Method
Abstract
We present some sufficient conditions on convergence of AOR method for solving Ax = b with A being a strictly doubly α diagonally dominant matrix. Moreover, we give two numerical examples to show the advantage of the new results.
1. Introduction
Let us denote all complex square matrices by Cn×n and all complex vectors by Cn.
For A = (aij) ∈ Cn×n, we denote by ρ(A) the spectral radius of matrix A.
2. Preliminaries
Definition 2.1 (see [2].)A matrix A ∈ Cn×n is called a strictly diagonally dominant matrix (SD) if
Definition 2.2 (see [3].)A matrix A ∈ Cn×n is called a strictly α diagonally dominant matrix (D(α)) if there exits α ∈ [0,1], such that
Definition 2.3 (see [4].)Let A = (aij) ∈ Cn×n, if there exits α ∈ [0,1] such that
In [3, 5, 6], some people studied the convergence of AOR method for solving linear system Ax = b and gave the areas of convergence. In [5], Cvetković and Herceg studied the convergence of AOR method for strictly diagonally dominant matrices. In [3], Huang and Wang studied the convergence of AOR method for strictly α diagonally dominant matrices. In [6], Gao and Huang studied the convergence of AOR method for strictly doubly diagonally dominant matrices.
Theorem 2.4 (see [3].)Let A ∈ D(α), then AOR method converges for
3. Upper Bound for Spectral Radius of Mσ,ω
In the following, we present an upper bound for spectral radius of AOR iterative matrix Mσ,ω for strictly doubly α diagonally dominant coefficient matrix.
Lemma 3.1 (see [4].)If A ∈ DD(α), then A is a nonsingular H-matrix.
Theorem 3.2. Let A ∈ DD(α), if 1 − σ2[αRi(L)Rj(L) + (1 − α)Si(L)Sj(L)] > 0, for all j ∈ N, i ≠ j, then
Proof. Let λ be an eigenvalue of Mσ,ω such that
If λ is an eigenvalue of Mσ,ω, then there exits at least a couple of i, j (i ≠ j), such that
4. Improving Results on Convergence of AOR Method
In this section, we present new results on convergence of AOR method.
Theorem 4.1. Let A ∈ DD(α), then AOR method converges if ω, σ satisfy either
Proof. It is easy to verify that for each σ, which satisfies one of the conditions (I)–(III), we have
Firstly, we consider case (I). Since A be a α diagonally dominant matrix, then by Lemma 3.1, we know that A is a nonsingular H-matrix; therefore, M(A) is a nonsingular M-matrix, and it follows that from paper [7], ρ(Mσ,σ) < 1 holds for 0 ≤ σ < s and for σ ≠ 0,
If 0 < ω < max {2σ/(1 + ρ(Mσ,σ)), t} = t, then it remains to analyze the case
- (1)
When ω ≤ 1, it easy to verify that (4.8) holds.
- (2)
When ω > 1, since
()
Secondly, we prove (II).
- (1)
When 0 < ω ≤ 1, σ < 0,
()By A2 − A3 < A1, we have()It is easy to verify that the discriminant Δ of the quadratic in σ satisfies Δ > 0, and so there holds()By σ < 0 and 1 − σ2[αRi(L)Rj(L) + (1 − α)Si(L)Sj(L)] > 0, for all i, j ∈ N, i ≠ j, we obtain() - (2)
When 1 < ω < t, σ < 0,
()By A2 − A3 < A1, we have()It is easy to verify that the discriminant Δ of the quadratic in σ satisfies Δ > 0, and so there holds()By σ < 0 and 1 − σ2[αRi(L)Rj(L) + (1 − α)Si(L)Sj(L)] > 0, for all i, j ∈ N, i ≠ j, we obtain()Therefore, by (4.16) and (4.20), we get()
Finally, we prove (III).
- (1)
When 0 < ω ≤ 1, σ ≥ t,
()By A2 − A3 < A1, we have()It is easy to verify that the discriminant Δ of the quadratic in σ satisfies Δ > 0, and so there holds()By σ ≥ t, we obtain() - (2)
When 1 < ω < t, σ ≥ t,
()By A2 − A3 < A1, we have()It is easy to verify that the discriminant Δ of the quadratic in σ satisfies Δ > 0, and so there holds()By σ ≥ t, we obtain()Therefore, by (4.25) and (4.29), we obtain()
We can obtain the following results easily.
Theorem 4.2. Let A ∈ DD(α). If Ri(L + U)Rj(L + U) − Si(L + U)Sj(L + U) > 0, when 0 < ω ≤ 1, the following conditions hold:
5. Examples
In the following examples, we give the areas of convergence of AOR method to show that our results are better than ones obtained by Theorems 2.4 and 2.5.
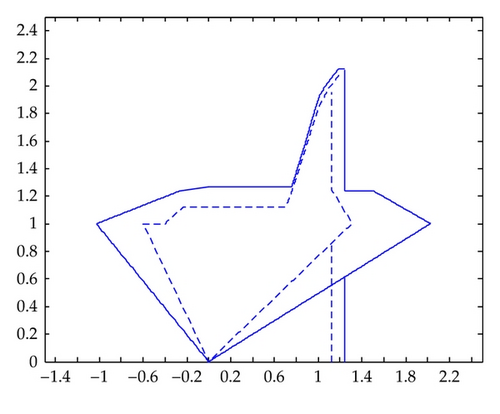
Now we give two figures. In Figure 1, we can see that the area of convergence obtained by Theorem 4.1 (real line) is larger than that obtained by Theorem 2.5 (virtual line). In Figure 2, we can see that the area of convergence obtained by Theorem 4.1 (real line) is larger than that obtained by Theorem 2.4 (virtual line). From above we know that the area of convergence obtained by Theorem 4.1 is larger than ones obtained by Theorems 2.5 and 2.4.

Acknowledgments
The authors would like to thank the referees for their valuable comments and suggestions, which greatly improved the original version of this paper. This work was supported by the National Natural Science Foundation of China (Grant no. 11001144) and the Science and Technology Program of Shandong Universities of China (J10LA06).




