Fatigue analysis of structural components such as helix tensile armors and steel tubes is a critical design issue for dynamic umbilicals and flexible pipes. The basis for assessment of fatigue damage of such elements is the long-term stress cycle distribution at critical locations on the helix elements caused by long-term environmental loading on the system. The long-term stress cycle distribution will hence require global dynamic time domain analysis followed by a detailed cross-sectional analysis in a large number of irregular sea states. An overall computational consistent and efficient fatigue analysis scheme is outlined with due regard of the cross-sectional analysis technique required for fatigue stress calculation with particular attention to the helix elements. The global cross-section is exposed to pure bending, tensile, torsion, and pressure loading. The state of the different cross-section elements is based on the global response. Special emphasis is placed on assessment of friction stresses caused by the stick-slip behavior of helix elements in bending that are of special importance for fatigue life assessments. The described cross-sectional analysis techniques are based on an extensive literature survey and are hence considered to represent industry consensus. The performance of the described calculation scheme is illustrated by case studies.

1. Introduction

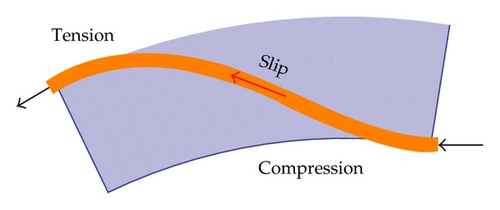
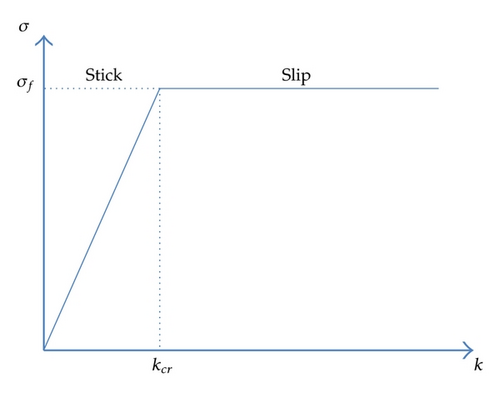
The required bending flexibility of risers and umbilicals is achieved by arranging strength and functional elements in a helix geometry. The helix geometry allows the elements to slip in order to release axial stresses built up by cross-sectional bending. This mechanism is essential for arranging flexible risers and umbilicals in compliant configurations that are capable of absorbing loads due to floater motions in harsh environmental conditions. The penalty is, however, that assessment of fatigue stresses in helix elements becomes complex due to the stick-slip behavior of helix elements in bending, as in Figure 1. The purpose of fatigue analysis is assessment of fatigue damage in all relevant elements in the cross-section for a long-term dynamic loading environment. Fatigue analysis of helix elements such as tensile armors and steel tubes is a critical design issue for umbilicals and flexible pipes. Critical areas are normally at the floater interface where bend limiting devices, that is, a bend stiffener or a bellmouth, are applied to avoid overbending in extreme load situations and reduce long-term fatigue loading, see, for example, [1, 2] for further details.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Slip of helix elements in bending.

ISO 13628-5 Subsea umbilicals [3] is the main reference for design and load-effect analysis of umbilicals. This standard requires that fatigue life will be calculated considering all relevant cyclic loading imposed on the umbilical over its design life. The most onerous fatigue loading for umbilicals in dynamic service is normally as follows:

(1)
Wave-induced fatigue loading due to direct wave loading and associated floater motions;
(2)
Vortex-induced vibration (VIV) in steady current conditions.

Both loading scenarios will require fatigue damage calculations in numerous short-term conditions to represent the long-term fatigue loading environment. As an example, wave-induced fatigue analyses will typically require stress calculation in about 100–300 stationary irregular sea states each with duration of 1 hour. In addition, an iterative analysis scheme is in general required for consistent assessment of fatigue damage caused by VIV due to the highly nonlinear stick-slip damping mechanism in bending, see [4] for details.

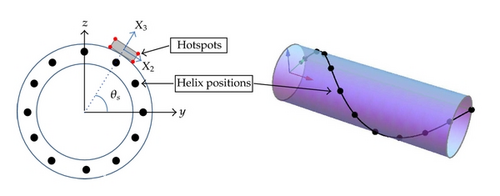
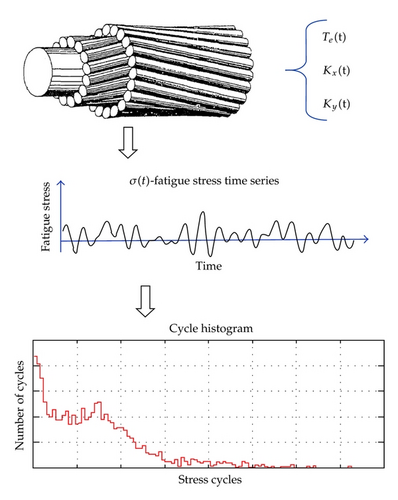
The basis for assessment of fatigue damage in helix elements is the long-term cycle distribution in several hot-spots, that is, critical positions on the helix cross-section, for a representative number of helix positions, that is, positions along the helix in one pitch, as shown in Figure 2.

The main challenge is hence to establish an overall manageable computational scheme to establish fatigue life estimates with sufficient confidence. A computational efficient cross-sectional analysis strategy is hence a vital part of the overall fatigue analysis approach. DNV has developed a dedicated computer program named Helica to address these design and analysis challenges [5, 6]. The main capabilities are as follows:

(i)
applicable to umbilicals, power cables, flexible risers, and similar unbonded structures;
(ii)
load sharing analysis for combined loading;
(iii)
calculation of cross-sectional stiffness properties: axial, bending, and torsion;
(iv)
fatigue stress analysis of helix elements considering stick-slip behavior in bending;
(v)
Calculation of consistent fatigue stresses by direct application of global response time series as external loading.
(vi)
calculation of capacity curves for the entire cross-section in compliance with applicable design codes;
(vii)
short-term fatigue life and long-term fatigue analysis capabilities;
(viii)
efficient and robust analysis scheme;
(ix)
well-documented transparent theoretical formulation representing industry consensus;

One of the main drivers behind this development has been to establish an efficient and consistent fatigue analysis scheme. The main focus of this paper is to give a detailed description of the cross-sectional response models applied to achieve an efficient and robust analysis scheme.

2. Numerical Model

2.1. Introduction

The computational model is based on an essential 2D formulation allowing for cross-sectional modeling of composite tubes containing helix elements in an unbonded structure. 2D is here to be understood as an average description where the averaging is applied in longitudinal pipe direction. The consequence of this is that possible 3D effects close to terminations can not be handled.

The helix elements are assumed to be arranged in well-defined layers allowing for treating each helix layer by means of an equivalent tube model with stiffness properties assembled from the individual helix elements. Different types of helix elements may be applied in the same layer to model, for example, umbilicals. Different distance from the cross-sectional centerline may also be specified for the individual elements in the same layer. All elements are assumed to have linear elastic material properties.

2.2. Response Models

The main purpose of the cross-sectional analysis is to predict the stresses in all interior elements for an applied external loading. In order to establish efficient response models for cross-sectional analysis, it is convenient to distinguish between the following load models, see Figure 3:

(i)
axis-symmetric loads due to effective tension, torsion moment, and internal and external pressure;
(ii)
pure bending, that is, constant global cross-section curvature.

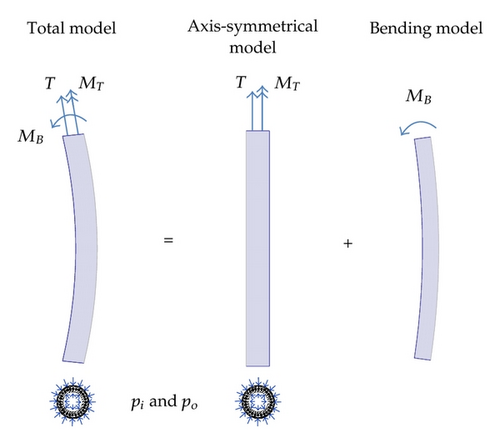
Separate response models are established for the different load conditions in order to obtain an overall robust, flexible, and computational efficient numerical solution scheme. The main purpose and underlying assumptions for these response models are discussed in the following. The purpose of the axis-symmetric response model is to establish the load sharing between the individual components of the cross-section as well as contact forces between the layers under axis-symmetric loading: effective tension, torsion, and hydrostatic pressure loads. This analysis requires a full model of the cross-section and needs to solve the overall static equilibrium with due regard to interlayer contact. Frictional effects are disregarded in the axis-symmetrical response model.

Effective tension is used to comply with other software used in this industry segment, like Riflex [7]. The use of effective tension is outlined in Sparks [8].

The bending response model is an analytical model for the calculation of stresses in helix elements due to cross-sectional bending. The stick-slip model is based on contact forces established by the axis-symmetrical analysis. A major advantage by the analytical bending model is that bending analysis of the helix elements can be carried out one by one without considering a complete model of the cross-section. This ensures a very flexible and efficient computation scheme. The main assumptions of the analytical bending model can be summarized as follows:

(i)
constant interlayer contact pressure found by axis-symmetrical analysis. Additional contact pressure induced by bending itself is neglected;
(ii)
friction/contact between helical elements in the same layer is neglected, for example, possible blocking/locking interlayer behavior can not be modeled explicitly;
(iii)
no end effects included, that is, bending takes place well away from terminations;
(iv)
constant global cross-sectional curvature is assumed;
(v)
axial slip of helix elements is assumed, that is, loxodromic helix geometry assumed during bending.

2.3. Axis-Symmetrical Response Model

2.3.1. General

The axis-symmetrical model is built up of concentric layers to model the entire cross-sections. All layers are assumed to have the same axial and torsional deformation, while the radial deformation is described separately for all layers. Each layer will hence have 1 or 2 radial degrees of freedom (dof) depending on whether the radial deformation of the layer itself is considered or not. The element types used in modeling and analysis are listed in Table 1.

Table 1. Typical elements used in modeling and analysis of axis-symmetrical response.

Element type	Assumption
Thin cylindrical element	Constant through thickness radial displacements; axial, circumferential, and in-plane shear strains: ε_xx, ε_θθ, and ε_xθ.
Thick cylindrical element	Logarithmic through thickness radial displacements; radial, axial, circumferential, and in-plane shear strains: ε_RR, ε_xx, ε_θθ, and ε_xθ.
Core element	Generalized cylinder element where the effect is expressed through and element stiffness matrix: k_ij.
Helix element	Helix element with axial strains only: ε₀₁₁.
Helix element	Helix element with axial strains, curvatures, and torsional shear strains: ε₀₁₁, κ₂, κ₃, and γ_s.

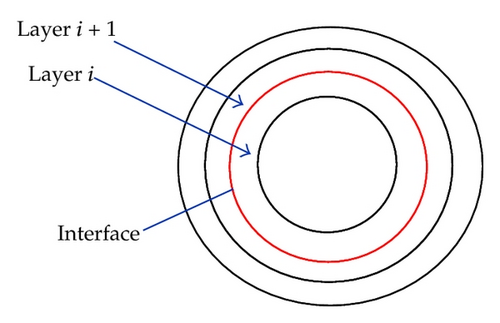
The cylinder layers are intended for modeling of concentric plastic/metallic sheaths, for example, inner/outer pressure barrier of flexible pipes and external/interior sheaths of umbilicals. The core element is intended for modeling of resulting stiffness properties of one or several layers. A typical application is modeling of resulting stiffness properties of underlying layers supporting one or several layers of cross-wound tensile amours. The helix layers are modeled as equivalent thin cylinder layers in the axis-symmetrical analysis. The equivalent cylinder layer is established by assembling the stiffness contributions from each helix component in the layer. The stiffness matrix of each helix element is derived based on slender beam theory assuming the as-produced nominal helix geometry as initial stress-free condition, that is, a state of no stress. The deformations and stresses of each helix component due to axis-symmetrical loading are hence uniquely described by the global axial, torsional, and radial deformation of each layer. Full details of all elements are given in Skeie [5] while the kinematics of the cylindrical and helix element are pursued next.

2.3.2. Kinematics

The kinematic description of the cylindrical and helical layers is essential for the response of the composite cross-section. The configuration may be described in parametric form. The cylinder is given by

()

i_j denotes the global coordinate system. A helix is a curve on the cylindrical surface following a fixed trajectory defined by the inclination angle, α. This yields also a relation between the helical axis denoted s and the polar angle θ. The helix geometry is thus a one-parameter specialization of the cylinder

()

It is noted that the relations hold both for the initial and deformed configuration of the geometry. An orthogonal local triad for the helix is expressed through

()

Depending on the length parameter, s, the triad forms an orthonormal set of base vectors as seen in the formulas in (2.3). The deformation of the cylinder consists of three independent components constant change of radius, linear change of angle, and linear extension of the overall cross-section. The undeformed and deformed geometries are related by

()

where we have used primed superscripts to denote the deformed configuration. The global displacement pattern yields a relation between the initial and deformed helix angles

()

There exists a relation between the initial curvilinear quantity s and the deformed measure s^′ given by

()

The trigonometric quantities are related by

()

Appropriate strain expressions may be derived from the kinematic relations. The Green-Lagrange strain measure is used in the following, and the linearized expressions are derived consistently. The general strain state in the helix elements is expressed in the form

()

where ε₀₁₁ is the beam axial strain, κ_α is the local beam curvature about the two local cross-section axes, and γ_s denotes the torsional shear strain. The different expression is derived from geometry and is linearized to yield

()

where

denotes linearization. The curvatures and shear strain terms are defined accordingly

()

where the subscript _,1 is used to denote differentiation with respect to the arc-length parameter s or direction 1. It is noted that the relation in (2.10) includes stretching of the helix centerline. Under the assumption that the extension of the centerline is small, it is customary to use the approximation

()

The detailed expressions are then given by

()

and are consistent with the equations given by Love [9] and also used in Witz and Tan [10]. The expressions may be used in the constitutive relations to derive stresses, cross-sectional properties, and global stiffness relations through the use of virtual work.

The strains, ε_RR, ε_xx, ε_θθ, and ε_xθ, in the cylindrical sheets may be found using equivalent expressions. The convective base vectors are defined by

()

The covariant linearized strain terms for a thin cylinder are expressed by

()

and similar for the other components such that

()

Physical relevant strain expressions appear when expressing them in an orthonormal cylindrical coordinate frame where

A thick cylinder is also considered where the radial deformation is assumed to vary according to

()

which then gives rise to radial strains

()

R_i and R_o denote the inner and outer cylinder radii, respectively.

2.3.3. Governing Equations

The global assembled system of equations for the axis-symmetrical analysis can hence be expressed as

()

The first equation expresses global equilibrium of the cross-section, while the latter states the impenetrability condition of the m interface layers, see Figure 4. K denotes the stiffness matrix assembled from all layers, R is the external load vector, while r is the displacement vector for all the unknown degrees of freedom (dof) in the system. Physically, the impenetrability equations allow for gaps to open between the layers, but they are not allowed to deform into each other. In order to support an efficient solution of the linear system of equations subjected to constraints, it is convenient to reformulate the problem as an associated quadratic programming (QP) problem. This is a special type of mathematical optimization problem that in our case reduces to

()

C is a matrix that expresses the interlayer impenetrability constraints discussed above. It is noted that the two formulations are equivalent and thus yield identical results. The advantage of the latter formulation is that it is widely studied in the literature, and a number of well established and robust solution schemes exists including the interior point method, active set methods, augmented Lagrangian methods, conjugate gradient methods, and gradient projections. The basis for solution of our quadratic programming problem is minimization of the augmented potential energy function which can be expressed as

()

where λ_i are denoted Lagrange multipliers. Karush-Kuhn-Tucker (KKH) conditions for impenetrability constraints are

()

It can be shown that the Lagrange multipliers are the contact forces between the layers. The QP solution scheme will hence yield both contact forces and layer displacements as direct output from the analysis. Layer displacements yield the stresses and strains in all interior elements of the cross-section, while the layer interface contact forces are crucial input to subsequent bending analysis of the helix elements. A concentric layer model, depicted in Figure 5, for solving the axis-symmetrical problem has been applied by several authors. However, the solution strategy proposed in this paper has proved to yield a very versatile an efficient axis-symmetrical solver. Extensive validation of the axis symmetrical response model has been conducted. Comparison to other published results [10–12] shows very good correlation, Table 2.

Table 2. Axis-symmetrical analysis results—comparison, Vaz et al. [11], Sævik and Bruaseth [12], and Skeie [5].

Feature	Test [11]	Vaz et al. [11]	Sævik and Bruaseth [12]	Skeie [5]
EA under tension, (MN)	70–101	82.9	100	79.5
Coupling—tension/torsion (m)		0.19	0.21	0.19
GJ clockwise, T = 0 kN(kNm²)	14.5–56.0	44.7	44.3	45.4
Coupling clockwise—torsion/tension, (rad/m)		182	188	180
GJ anticlockwise, T = 0 kN(kNm²)	15.9–17.2	19.1	19.5	18.7
Coupling anticlockwise—torsion/tension, (rad/m)		−406	−330	−343

2.4. Bending Model

2.4.1. General

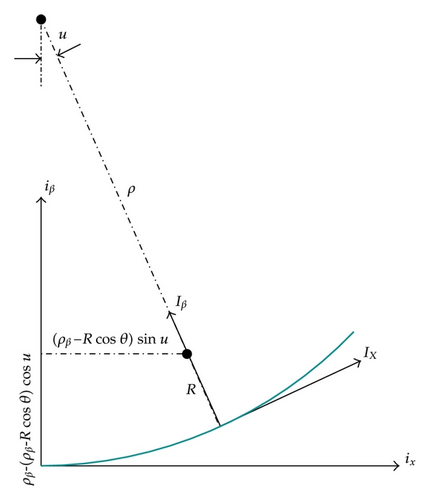
The additional stresses due to bending can be derived by assuming that the helix follows a loxodromic curve during cross-sectional bending. This means that the helix remains in its original position on the supporting cylinder surface during bending, and that it slips in axial direction. This geometrical assumption has gained consensus in the literature, see, for example, [13–15]. Experiments have also been conducted to validate this assumption, see, for example, [16]. Based on this geometrical assumption, it is fairly straightforward to establish the stress components during bending, see, for example, [13, 14]. Full details are given in [5].

The main stress components in a helix element during bending are the following:

(i)
local bending stress due to bending about local weak/strong axes of the helix,
(ii)
friction stress due to the stick/slip behavior in bending.

It is noted that other models for bending exist and especially the path followed by the helix when it slips, a loxodromic or the geodesic path. The subject is pursued in a number of publications, and discussions may be found in Féret and Bournazel [17], Out and von Morgan [18], Kraincanic and Kebadze [14], and Østergaard et al. [19] among others.

2.4.2. Kinematics

The undeformed configuration of the helical element is described in Section 2.3.2. The model now considers a pure bending behavior, and the deformed configuration is thus a torus. The parametric representation of the torus may be written as

()

where ρ_β is the radius of curvature in the β direction, and the global coordinate is located at the center of the bent cylinder. i_j denotes the global coordinate frame, while i_β is the axis of curvature, while

is the axis that is not bent. This is shown in Figure 6. The formulas hold for i_β = i_y and a careful use of the right sign should be exercised when i_β = i_z. The helix element lay on the loxodromic curve which, again, is a specialization of the torus

()

where we have used

()

The axial strains may be derived in the same way as in Section 2.3.2,

()

and the same for the curvatures and shear strain

()

where again we have used the approximation that

is a unit vector.

2.4.3. Stick-Slip Behavior

The local bending stresses can be expressed as

()

where E is the Young’s modulus, α is the helix lay angle, and κ_β denotes the cross-sectional curvature with the radius in β-axis direction. X₂ and X₃ are the local coordinates for calculation of bending stresses, see Figure 2. It should be noted that the local bending stress only depends on the cross-sectional curvature and is hence not linked to the stick-slip behavior of the helix element in bending. These stress components may therefore be computed separately. A response model for the stick-slip behavior can be established by considering the equilibrium between axial force built up in the helix element due to bending and the friction forces restraining axial displacement, see Figure 7. Equilibrium considerations in axial direction of an infinitesimal helix element give the following slip criterion:

()

where N denotes the axial force in helix element, and f is the available friction force per unit length.

Thus, slip will start when the tension gradient exceeds the available friction. This criterion governs onset of slip, but it gives no information on the behavior of the helix after slip initiation. Equilibrium considerations between slip/stick parts of the helix are required to study the slip progression after onset. Assuming that the helix element is completely fixed on the supporting cylinder, the axial force due to cross-sectional bending is given by

()

where R is the helix radius, A is the helix cross-sectional area, and θ_s is helix position angle. This stick force is valid for the situation where the friction force between the helix element and supporting cylinder prevents axial slip of the helix element. The corresponding axial force gradient can hence be expressed as

()

This expression shows that a significant force gradient will develop along a helix fixed to a supporting cylinder bent to a constant curvature. It is seen that the axial force gradient is largest at the neutral axis, θ_s = 0. Slip will hence start at the neutral axis. The critical curvature for onset of slip at the neutral axis is given by

()

The available friction can be determined from the axis-symmetric analysis by the following expression:

()

μ_i and μ_o are the inner- and outer-side friction coefficient, respectively, and q_i and q_o denotes the associated inner and outer contact force per unit length along the helix. After onset, the slip will progress along the helix away from the neutral axis for increasing curvature as illustrated in Figure 8. To find an expression for the slip progression after onset, it is required to consider the equilibrium between the slip-stick parts of the helix. The total friction force F over a distance s from the neutral axis along the helix is

()

By conservatively assuming that the slope is maintained and considering the equilibrium between the friction force, F, and the stick force, N, at distance s from the neutral axis this gives

()

It is observed that full slip is obtained for θ_s = π/2 giving

()

Friction stress σ_f, shown in Figure 9, is defined as the axial stress in the helix element at slip due to cross-sectional bending. Friction stress can hence be expressed as

()

This simple formula gives the basic relations between the governing geometric parameters and the friction stress. The friction stress is zero at the neutral axis and increases linearly to its maximum value for a helix position normal to the bending axis. The maximum friction stress

and the corresponding friction stress range

are given as

()

These expressions allow for simple conservative assessments of effects from friction stress to the fatigue life of the helix elements without performing bending analysis of the entire cross-section. For practical analysis, it is required that the analytical bending model shall be able to predict helix stresses in an arbitrary helix position due to external loading from biaxial bending and effective tension time histories. The following extensions of the described model are required to meet these requirements:

(i)
Extend formulations given in 1st quarter pitch to arbitrary helix positions.
(ii)
Implementation of stick—slip stress hysteresis formulation.
(iii)
Extend formulas given for bending about β^′-axis to bi-axial bending.

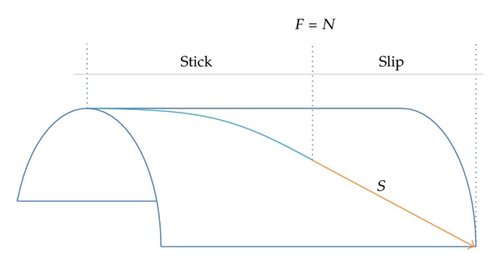
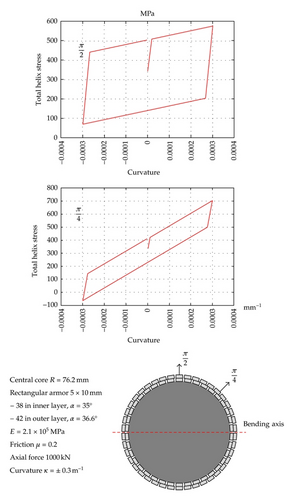
This generalization is fairly straight forward but somewhat detailed. A detailed description is therefore not given, but it suffice to note that the approach is based on the definition of proper sign convention, symmetry observations and proper bookkeeping of curvature reversals.

An example of the performance of the bending hysteresis model for tensile armor stresses is displayed in the Figure 10 for a harmonic curvature loading history. A significant variation in the effect from friction stress for different helix positions is observed. This underlines the importance of consistent treatment of friction stresses due to bi-axial bending in fatigue analysis of helix elements.

3. Case Studies

3.1. Capacity Curves

The extreme stress capacity is most conveniently determined in terms of a cross-sectional capacity curve. ISO 13628-5 Subsea umbilicals [3] describes allowable combinations of curvature and effective tension that can be applied to the cross-section without compromising the structural integrity of the interior strength and functional elements. Examples of umbilical capacity curves are shown in Figure 11 for different utilization levels reflecting different modes of operation, for example, installation and in-place operation. The utilization level is defined according to allowable stress levels, σ_a, related to the yield stress, σ_a = k_uσ_y, where σ_y denotes the yield stress, and k_u is a utilization factor. Similar considerations also hold for strains that are typically used for plastic sheaths. The methodology as outlined in the previous section is applied to determine stresses in all interior elements for combined tension and curvature loading. The utilization in each component is evaluated against acceptance criteria given in, for example, [3] or other relevant design codes. The capacity curve is finally established as the allowable effective tension and curvature combinations that ensure that the stresses in all interior elements fulfill the defined acceptance criteria. A recursive calculation scheme is applied for consistent calculation of capacity curves of cross-sections with higher-order composite helix elements, for example, cables applied in helix geometry in the cross-section [5, 6]. The procedure is as follows:

(1)
establish capacity curve and resulting stiffness properties of the composite helix component. This is done by a separate straightforward cross-sectional analysis using a cross-sectional model of the composite helix component only;
(2)
include composite helix component in the total cross-sectional model in terms of equivalent stiffness—geometrical parameters established from (1). Load sharing analysis yields tension as well as local curvature acting on the composite helix component. Utilization in the composite helix component is then based on the capacity curve from (1).

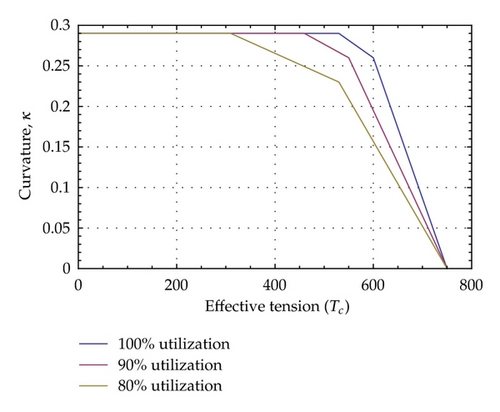
Several levels of recursive calculation can be applied to establish consistent capacity curves of complex cross-sectional layouts. The main benefit of the recursive calculation scheme is that very complex cross-sections can be subdivided into simpler components that can be solved by standard cross-section analysis without having to build a comprehensive overall cross-sectional model.

3.2. Fatigue Analysis

3.2.1. System Description

Fatigue analysis of rectangular cross-wound tensile armors of an umbilical operated from a turret-moored FPSO in typical Norwegian environmental conditions is considered [20]. The umbilical is arranged in a classic wave configuration with bend stiffener interface to the floater, see Figure 12. The fatigue loading environment is described by the omnidirectional wave scatter diagram.

3.2.2. Analysis Methodology

The main steps in the fatigue analysis are the following:

(i)
discretization of the wave scatter diagram into representative number of blocks. Each block covers several sea states in the wave scatter diagram. 30 blocks are used in the present study to represent the long-term fatigue loading;
(ii)
perform global response analyses for all blocks in the wave scatter diagram considering all heading and direction combinations as defined in Table 3. A total of 270 short-term global response analyses is hence required to describe the long-term fatigue loading on the system;
(iii)
perform helix fatigue analysis for all fatigue loading conditions using simultaneous time histories of biaxial curvature and effective tension from the global analysis as input.

Table 3. Fatigue load case description.

Vessel heading (deg)	Direction	Probability of vessel heading per direction
0	Near	60%
15	Near	30%
30	Near	10%
0	Far	60%
15	Far	30%
30	Far	10%
0	Cross	60%
15	Cross	30%
30	Cross	10%

The methodology as outlined in [21] is used as basis for the wave scatter diagram discretization to achieve fatigue life estimates with adequate statistical confidence.

Global nonlinear time domain dynamic analysis is conducted by means of the Riflex finite element analysis (FEA), [7], computer program for static and dynamic analysis of slender marine structures. Dynamic simulations with duration of 1 hour are conducted in each block of the wave scatter diagram considering random wave loading. Response time histories are stored for subsequent fatigue analysis at 76 locations along the umbilical covering potential critical areas including bend stiffener area, buoyancy section, and touch-down area. The main steps in the subsequent short-term helix fatigue analysis conducted for each fatigue load case are the following:

(i)
establish fatigue stress time histories at all locations/hotspots. This analysis is performed by combined axis-symmetrical analysis and bending analysis at each time step. In this way, the interlayer contact forces governing the stick-slip bending response are updated according to the instantaneous effective tension loading;
(ii)
establish cycle histogram by rain flow counting of the generated fatigue stress time.

This procedure is outlined in Figure 13. The long-term helix fatigue analysis consists of the following steps:

(i)
accumulate long-term cycle histograms at all locations/hotspots with due consideration of the probability of occurrence of the short-term fatigue loading conditions;
(ii)
establish fatigue life from the long-term cycle histograms.

Key figures for the helix fatigue analysis are summarized in Table 4. The key figures for the global analyses and subsequent fatigue analyses show that the computational efforts required are substantial. It should be emphasized that this example is of representative size for this type of analysis.

Table 4. Key figures for the helix fatigue analysis.

Number of hot-spots (corner points)	4
Number of helix locations	12
Total number of fatigue stress time series calculations of 1-hour duration (270 × 76 × 4 × 12)	984960

3.2.3. Evaluation of Results and Numerical Performance

Analyses have been conducted with two different models for stress calculation:

(i)
helix model with stick-slip modeling included;
(ii)
helix model with no friction.

The latter model is included as a reference case only. This approach produce quite similar results as the so-called straight tube analogy (STA) widely used in the industry for fatigue life assessment of helix structures. The long-term cycle distribution and corresponding fatigue damage is shown in Figure 14 for the most critical hot-spot location. The following can be concluded:

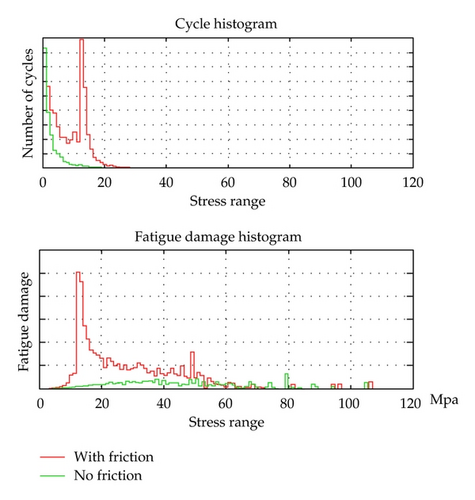
(i)
a pronounced peak in the cycle histogram is observed at 15 MPa. This corresponds to the maximum friction stress range;
(ii)
the effect from frictional stresses is decisive for fatigue life prediction. Consistent treatment of the stick-slip behavior in bending is hence essential;
(iii)
a substantial part of the fatigue damage can be attributed to the upper part of the stress cycle histogram, that is, to relatively few large stress cycles. It is therefore essential that the duration of the short-term simulations is sufficient to give a representative frequency of large stress cycles.

The total computation time for the helix fatigue analysis on a standard single core lap top is about 5 hours. The computation time is highly acceptable considering the size of the problem. Parallel computing functionality is included in the software; thus, the computation time may be reduced proportional to the number of available processors. No numerical instabilities or anomalies were detected.

4. Conclusions

An overall computational consistent and highly efficient helix fatigue analysis scheme has been established. This has been achieved by combined use of a versatile and efficient axis-symmetrical solver with an analytical helix bending model. This model ensures full consistency with the global response model as the computational efficiency allows for application of global response time histories as direct loading on the cross-sectional response model. The effect from frictional stresses is decisive for fatigue life prediction. Consistent treatment of the stick-slip behavior in bending is hence essential for fatigue life prediction on nonbonded cross-sections containing helix elements.

References

1 Sødahl N. and Ottesen T., Bend stiffener design for umbilicals, Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE ′11), 2011, Rotterdam, The Netherlands.
Google Scholar
2 Rustadand A. M., Sødahl N., Kalleklev A. J. et al., Use of weight elements to improve the dynamic performance of umbilicals, 5, Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering (OMAE ′10), 2010, Shanghai, China, 171–175, https://doi.org/10.1115/OMAE2010%2D20118.
10.1115/OMAE2010-20118
Google Scholar
3 Petroleum and natural gas industries design and operation of subsea production systems, part 5, Subsea umbilicals, 2009.
Google Scholar
4 Sødahl N., Steinkjer O., Gjølmesli E., and Hansen-Zahl K., Consistent VIV analysis methodology for umbilicals, Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE ′11), 2011, Rotterdam, The Netherlands.
Google Scholar
5 Skeie G., Cross sectional analysis of flexible pipes and umbilicals, 2006, no. 2122, DNV Research & Innovation.
Google Scholar
6 Sødahl N., Steinkjer O., and Bahiense R., Helica Users Manual, 2009, DNV.
Google Scholar
7 Marinetek, Riflex User Manual, 2009.
Google Scholar
8 Sparks C. P., Influence of tension, pressure and weight on pipe and riser deformations and stresses, Journal of Energy Resources Technology, Transactions of the ASME. (1984) 106, no. 1, 46–54.
10.1115/1.3231023
Web of Science® Google Scholar
9 Love A. E. H., A Treatise on the Mathematical Theory of Elasticity, 1944, 4th edition, Dover, New York, NY, USA, 0010851, ZBL0063.03651.
Google Scholar
10 Witz J. A. and Tan Z., On the axial-torsional structural behavior of flexible pipes, umbilicals and marine cables, Marine Structures. (1992) 5, 205–227, https://doi.org/10.1016/0951%2D8339(92)90029%2DO.
10.1016/0951-8339(92)90029-O
Google Scholar
11 Vaz M.A., Aguiar L. A. D., Estefen S. F., and Brack M., Experimental determination of axial, torsional and bending stiffiness of umbilical cables, Proceedings of the 17th International Offshore & Arctic Engineering Conference (OMAE ′98), 1998, Fairfield, NJ, USA.
Google Scholar
12 Sævik S. and Bruaseth S., Theoretical and experimental studies of the axisymmetric behaviour of complex umbilical cross-sections, Applied Ocean Research. (2005) 27, no. 2, 97–106, https://doi.org/10.1016/j.apor.2005.11.001.
10.1016/j.apor.2005.11.001
Web of Science® Google Scholar
13 Witz J. A. and Tan Z., On the exural structural behavior of flexible pipes, umbilicals and marine cables, Marine Structures. (1992) 5, 229–249, https://doi.org/10.1016/0951%2D8339(92)90030%2DS.
10.1016/0951-8339(92)90030-S
Google Scholar
14 Kraincanic I. and Kebadze E., Slip initiation and progression in helical armouring layers of unbonded flexible pipes and its effect on pipe bending behaviour, The Journal of Strain Analysis for Engineering Design. (2001) 36, no. 3, 265–275, https://doi.org/10.1243/0309324011514458.
10.1243/0309324011514458
Web of Science® Google Scholar
15 Sævik S. and Ekeberg K. I., Non-linear stress analysis of complex umbilical cross-sections, 1, Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering (OMAE ′02), June 2002, 211–217, ASME Conference Proceedings, https://doi.org/10.1115/OMAE2002%2D28126.
10.1115/OMAE2002-28126
Google Scholar
16 Dobson A. and Fogg D., Fatigue testing and analysis of a deep water steel tube umbilical, 3, Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering (OMAE ′08), June 2008, 133–140, ASME Conference Proceedings, https://doi.org/10.1115/OMAE2008%2D57151.
10.1115/OMAE2008-57151
Google Scholar
17 Féret J. J. and Bournazel C. L., Calculation of stresses and slip in structural layers of unbonded flexible pipes, Journal of Offshore Mechanics and Arctic Engineering. (1987) 109, no. 3, 263–269, https://doi.org/10.1115/1.3257019.
10.1115/1.3257019
Google Scholar
18 Out J. M. M. and von Morgen B. J., Slippage of helical reinforcing on a bent cylinder, Engineering Structures. (1997) 19, no. 6, 507–515, https://doi.org/10.1016/S0141%2D0296(96)00112%2D5.
10.1016/S0141-0296(96)00112-5
Web of Science® Google Scholar
19 Østergaard N. H., Lyckegaard A., and Andreasen J. H., A method for prediction of the equilibrium state of a long and slender wire on a frictionless toroid applied for analysis of flexible pipe structures, Engineering Structures. (2012) 34, no. 1, 391–399, https://doi.org/10.1016/j.engstruct.2011.10.012.
10.1016/j.engstruct.2011.10.012
Web of Science® Google Scholar
20 Sødahl N., Skeie G., Steinkjer O., and Kalleklev A. J., Effcient fatigue analysis of helix elements in umbilicals and flexible risers, 5, Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering (OMAE ′10), June 2010, Shanghai, China, 1029–1037, ASME Conference Proceedings, https://doi.org/10.1115/OMAE2010%2D21012.
10.1115/OMAE2010-21012
Google Scholar
21 Steinkjer O., Sødahl N., and Grytøyr G., Methodology for time domain fatigue life assessment of risers and umbilicals, Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering (OMAE ′10), June 2010, Shanghai, China, 177–184, ASME Conference Proceedings, https://doi.org/10.1115/OMAE2010%2D20119.
10.1115/OMAE2010-20119
Google Scholar

Citing Literature

All articles

Efficient Fatigue Analysis of Helix Elements in Umbilicals and Flexible Risers: Theory and Applications

Abstract

1. Introduction