Journal of Applied Mathematics
Volume 2012, Issue 1 236281
Research Article
Open Access

A New Family of Phase-Fitted and Amplification-Fitted Runge-Kutta Type Methods for Oscillators

Zhaoxia Chen, 

Zhaoxia Chen

Department of Applied Mathematics, Nanjing Agricultural University, Nanjing 210095, China njau.edu.cn

Search for more papers by this author
Xiong You, 

Corresponding Author

Xiong You

Department of Applied Mathematics, Nanjing Agricultural University, Nanjing 210095, China njau.edu.cn

State Key Laboratory for Novel Software Technology at Nanjing University, Nanjing 210093, China nju.edu.cn

Search for more papers by this author
Xin Shu, 

Xin Shu

Department of Applied Mathematics, Nanjing Agricultural University, Nanjing 210095, China njau.edu.cn

Department of Computer Science and Engineering, Shanghai Jiaotong University, Shanghai 200240, China sjtu.edu.cn

Search for more papers by this author
Mei Zhang, 

Mei Zhang

Department of Applied Mathematics, Nanjing Agricultural University, Nanjing 210095, China njau.edu.cn

Search for more papers by this author
First published: 23 October 2012
https://doi.org/10.1155/2012/236281
Citations: 3
Academic Editor: Jesus Vigo-Aguiar

Abstract

In order to solve initial value problems of differential equations with oscillatory solutions, this paper improves traditional Runge-Kutta (RK) methods by introducing frequency-depending weights in the update. New practical RK integrators are obtained with the phase-fitting and amplification-fitting conditions and algebraic order conditions. Two of the new methods have updates that are also phase-fitted and amplification-fitted. The linear stability and phase properties of the new methods are examined. The results of numerical experiments on physical and biological problems show the robustness and competence of the new methods compared to some highly efficient integrators in the literature.

1. Introduction

A vast of problems in applied fields, such as elastics, mechanics, astrophysics, electronics, molecular dynamics, ecology, and biochemistry, can be cast into the form of an initial value problem of the system of first-order ordinary differential equations as follows:
()
where y ∈ ℝd,   f : ℝ × ℝd → ℝd is a sufficiently smooth function. Traditionally, the problem (1.1) has been solved numerically by Runge-Kutta methods (RK) or linear multistep methods (LMMs) (see [1–3]). In many applications, the solution to the problem (1.1) is oscillatory or periodic. But the general-purpose methods do not take into account the oscillatory feature of the problem and the numerical results they produce are generally not satisfactory.

Recently, some authors have proposed to adapt traditional integrators to the oscillatory character of the solution to the problem (1.1) (see [4–7]). Bettis [8] constructs a three-stage method and a four-stage method which solve the equation y′ = iωy    (i2 = −1) without truncation error. Paternoster [9] develops a class of implicit methods of Runge-Kutta (RK) and Runge-Kutta-Nyström (RKN) types by the trigonometric fitting technique. For oscillatory problems which can be put in the form of a second-order equation y′′ = f(x, y), Franco [10] improves the update of the classical RKN methods and proposes a family of explicit RKN methods adapted to perturbed oscillators (ARKN) and a class of explicit adapted RK methods in [11]. Anastassi and Simos [12] construct a phase-fitted and amplification-fitted RK method of “almost” order five. Van de Vyver [13] investigates phase-fitted and amplification-fitted two step hybrid methods (FTSH). For other important work on frequency dependent integrators for general second-order oscillatory equations, the reader is referred to [14–18]. Many authors focus on effective numerical integration of specific categories of oscillatory problems. For example, Vigo-Aguiar and Simos [18] construct an exponentially fitted and trigonometrically fitted method for orbital problems. The papers [19–21] have designed highly efficient integrators for the Schrödinger equation.

Based on the previous work, we consider, in this paper, phase-fitted and amplification-fitted RK type integrators whose coefficients in the update depend on the product of the fitting frequency and the step size. In Section 2, we present a result on order conditions for frequency-depending modified Runge-Kutta type methods. Section 3 introduces the notion of phase-fitted and amplification-fitted RK type methods (FRK) and derives the phase-fitting and amplification-fitting conditions. In Section 4 two FRK methods of order four and two FRK methods of order five are constructed. Their error coefficients and error constants are also calculated. The linear stability and phase properties of the new FRK methods are analyzed in Section 5. In Section 6, numerical experiments are carried out to illustrate the effectiveness and superiority of our new methods compared to two well-known highly efficient integrators we have chosen from the recent literature. Section 7 is devoted to conclusive comments.

2. Order Conditions for RK Type Methods with Frequency-Dependent Weights

Assume that the principal frequency of the problem (1.1) is known or can be accurately estimated in advance. This estimated frequency is denoted by ω, which is also called the fitting frequency. We consider the following s-stage modified Runge-Kutta method:
()
where h is the step size, ci, aij, i, j = 1, …, s are real numbers, and bi(ν),  i = 1, …, s are even functions of ν = hω. The scheme (2.1) can be represented by the Butcher tableau as follows:
()
or simply by (A, b, c). Conventionally, we assume that
()
As explained in [3], the order conditions for the modified RK method (2.1) can be derived by just considering the autonomous equation y′ = f(y). Using Butcher′s rooted tree theory in [1], the exact solution to the problem (1.1) and the numerical solution produced by the modified RK type method (2.1) have the B-series expressions as follows:
()
where the trees t, the functions ρ(t) (order), α(t) (number of equivalent trees), γ(t) (density), Φ(t) = (Φ1(t), …, Φs(t)) T (the s × 1 vector of elementary weights), and the elementary differentials ℱ(t)(y0) are defined in [3]. Then the local truncation error has the following series expansion:
()
If for any (p + 1)th differentiable function f(y), when the scheme (2.1) is applied to the problem (1.1), the local truncation error LTE = y(x0 + h) − y1 = 𝒪(hp+1), then the method (2.1) is said to have (algebraic) order p.

Theorem 2.1 (see Franco [11].)The modified RK type method (2.1) has order p if and only if the following conditions are satisfied:

()

If the method (2.1) is of order p, then we have
()
where ϵ(t) = 1 − γ(t)bTΦ(t) is called the error coefficient associated with the tree t of order p + 1 which is involved in the leading term of the local truncation error. Denote
()
The positive number
()
is called the error constant of the method.

3. Phase-Fitted and Amplification-Fitted Conditions

For oscillatory problems, as suggested by Paternoster [9] and Van der Houwen and Sommeijer [22], apart from the algebraic order, the analysis of phase lag and dissipation is important. To this end, we consider the following linear scalar equation:
()
The exact solution of this equation with the initial value y(x0) = y0 satisfies
()
where R0(z) = exp (z),   z = iν. This means that after a period of time h, the exact solution experiences a phase advance ν = hω and the amplification remains constant.
An application of the modified RK method (2.1) to (3.1) yields
()
where
()
Thus, after a time step h, the numerical solution obtains a phase advance argR(z) and the amplification factor |R(iν)|. R(z) is called the stability function of the method (2.1). Denote the real and imaginary part of R(z) by U(ν) and V(ν), respectively. Then, for small h, we have
()
For small h, argR(z) = tan−1(V(ν)/U(ν)) and . The above analysis leads to the following definition.

Definition 3.1 (see [22].)The quantities

()
are called the phase lag (or dispersion) and the error of amplification factor (or dissipation) of the method, respectively. If
()
then the method is called dispersive of order q and dissipative of order p, respectively. If
()
the method is called phase-fitted (or zero-dispersive) and amplification-fitted (or zero-dissipative), respectively. A modified RK method which is phase-fitted and amplification-fitted is called in short an FRK method.

It is interesting to consider the phase properties of the update of the scheme (2.1). Suppose that the internal stages have been exact for the linear equation (3.1), that is, Yi = exp (iciν)y0, then the update gives
()
where
()
Denote the real and imaginary part of Ru(z) by Uu(ν) and Vu(ν), respectively. Then, for small h,
()

Definition 3.2. The quantities

()
are called the phase lag (or dispersion) and the error of amplification factor (or dissipation) of the update of the method, respectively. If
()
then the update of the method is called dispersive of order q and dissipative of order p, respectively. If
()
the update of the method is called phase-fitted (or zero-dispersive) and amplification-fitted (or zero-dissipative) in the update, respectively.

Generally speaking, a traditional RK method with constant coefficients inevitably carries a nonzero phase lag and a nonzero error of amplification factor when applied to the linear oscillatory equation (3.1). Therefore, they are neither phase-fitted nor amplification-fitted. So does the update. For example, the classical RK method of order four with constant coefficients (denoted as RK4, see [3]) given by
()
has a phase lag and an error of amplification factor as follows:
()
For the update,
()
Therefore, both the method and its update are dispersive of order four and dissipative of order five.

The following theorem gives the necessary and sufficient conditions for a modified RK method and its update to be phase-fitted and amplification-fitted, respectively.

Theorem 3.3. (i) The method (2.1) is phase-fitted and amplification-fitted if and only if

()

(ii) The update of the method (2.1) is phase-fitted and amplification-fitted if and only if

()

The proof of this theorem is immediate.

4. Construction of New Methods

Now we proceed to construct modified RK type methods that are both phase-fitted and amplification-fitted based on the internal coefficients of two classical RK methods. For convenience we restrict ourselves to explicit methods.

4.1. Fourth-Order Methods

Consider a four-stage modified RK method with the following Butcher tableau:
()
For s = 4, the phase-fitting and amplification-fitting conditions (3.18) have the following form:
()
On the other hand, the first-order and second-order conditions become
()
Here, for the purpose of deriving the weights of the method, the higher order terms in the order conditions are omitted. We will follow this convention in the sequel. Solving (4.2) and (4.3), we obtain
()
As ν → 0, bi(ν) have the following Taylor expansions:
()
By direct calculation, we obtain the following expansions:
()
where the dot “·” between two vectors indicates componentwise product, and c2 and c3 indicate the componentwise square of the vector. We will follow the convention in the sequel. Thus, the coefficients given by (4.1) and (4.4) satisfy all the conditions of order four in Theorem 2.1. But they cannot satisfy all the conditions of order five. For instance,
()
Therefore, this method is of order four. The method was originally obtained by Simos [23] and we denote it by Simos4.
Corresponding to the nine fifth-order rooted trees t5j, j = 1, …, 9, the error coefficients of Simos4 are given by
()
Then for Simos4,
()
where
()
Now we require that the update of the method (4.1) is phase-fitted and amplification-fitted. By Theorem 3.3 (ii), we have
()
Solving (4.2) and (4.11), we obtain
()
where
()
It can be verified that the method given by (4.1) and (4.12) is of order four. We denote the method by FRK4.
The error coefficients of FRK4 are given by
()
where
()
Then for FRK4, we have
()

It can be seen that as ν → 0, both the methods Simos4 and FRK4 reduce to a classical RK method of order four (on page 138 of [3]), which we denote by RK4. The method RK4 is called the prototype method or the limit method of the methods Simos4 and FRK4. Moreover, as ν → 0, both Simos4 and FRK4 have the same error constant as that of RK4: .

4.2. Fifth-Order Methods

Consider the following modified RK type method with FSAL property, the prototype of which can be found on page 167 of [2] or on page 178 of [3],
()
For the method (4.17), the phase-fitting and amplification-fitting conditions (3.18) become
()
Combining these two equations and the following sufficient conditions in Theorem 2.1 corresponding the trees of orders one, two, and three, we have
()
Solving (4.18) and (4.19), we obtain
()
As ν → 0, we obtain the following expansions:
()
By simple computation, we have
()
By Theorem 2.1, the coefficients given by (4.17) and (4.20) satisfy all the conditions of order five. But it cannot satisfy all the conditions of order six. For example,
()
Therefore, this method is of order five and we denote it as FRK5a.
Corresponding to the twenty sixth-order rooted trees t6j, j = 1, …, 20, the error coefficients of FRK5a are given by
()
Then for FRK5a, we have
()
where
()
Now we require that the update of the method (4.17) is phase-fitted and amplification-fitted. By Theorem 3.3 (ii), we have
()
We can solve the algebraic systems (4.18), (4.27), and the last two equations in (4.19) for bi(ν). The closed expressions for bi(ν) is too complicated. As ν → 0, they have the series expressions as follows:
()

It can be verified that the method given by (4.17) and (4.28) is of order five. We denote the method by FRK5b.

The error coefficients of FRK5b are given by
()
Then for FRK5b, we have
()

It can be seen that as ν → 0, both the methods FRK5a and FRK5b reduce to a classical RK method of order five (on page 178 of [3]), which we denote by RK5. The method RK5 is called the prototype method or the limit method of the methods FRK5a and FRK5b. Moreover, as ν → 0, both FRK5a and FRK5b have the same error constant as that of RK5: .

5. Analysis of Stability and Phase Properties

In order to investigate the linear stability of the methods (2.1) or any other frequency-depending method, we applied it to the linear test equation as
()
One step of computation yields
()
where
()
is called the stability matrix of the method (2.1).

Definition 5.1. The region in the μ-ν plane Ω = {(μ, ν)∣μ > 0, ν > 0, |R(iμ, iν) : ≤1} is called the imaginary stability region of the method (2.1) and the closed curve defined by |R(iμ, iν)| = 1 is called the stability boundary of the method.

The imaginary stability regions of the methods Simos4, FRK4, FRK5a and FRK5b are depicted in Figures 1 and 2.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
The imaginary stability region of Simos4 (a) and FRK4a (b).
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
The imaginary stability region of Simos4 (a) and FRK4a (b).
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The imaginary stability region of FRK5a (a) and FRK5b (b).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The imaginary stability region of FRK5a (a) and FRK5b (b).

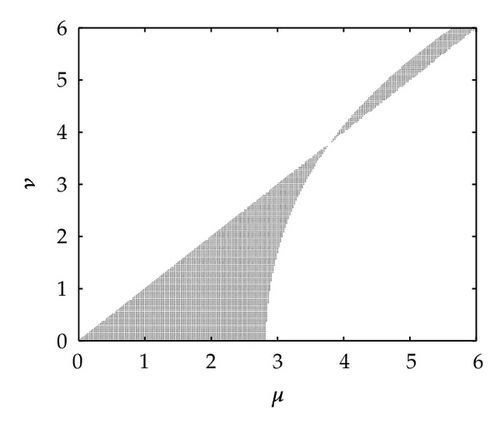
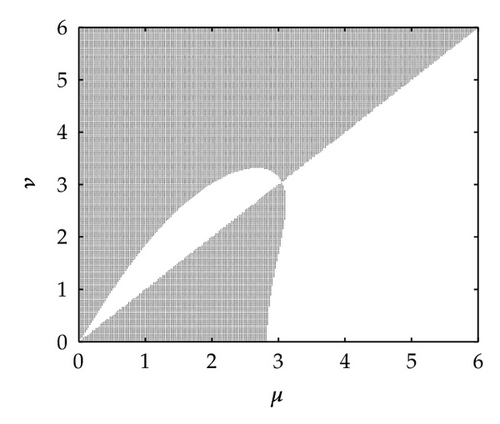
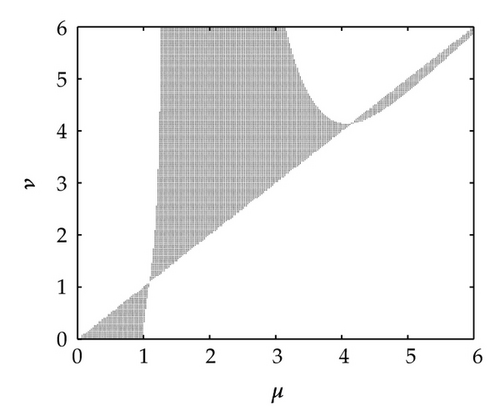
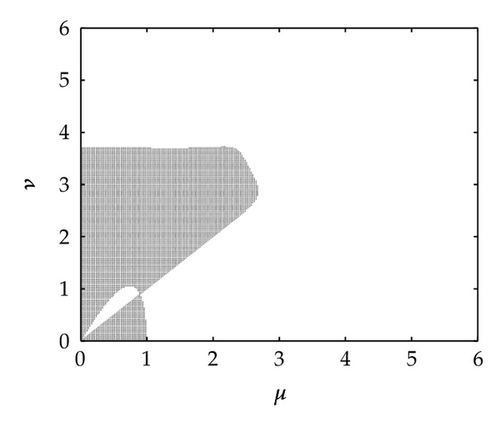
Definition 5.2. The quantities

()
are called the phase lag and the error of amplification factor of the method (2.1), respectively. If ϕ(μ, ν) = 𝒪(μq+1), and d(μ, ν) = 𝒪(μp+1), then the method (2.1) is said to be dispersive of order q and dissipative of order p, respectively (see Ozawa [24] and Van de Vyver [25]).

By definition, an FRK method has zero phase lag and zero dissipation when applied to the standard linear oscillator (5.1) whose frequency λ coincides with the fitting frequency ω. That is to say, ϕ(μ, μ) = 0,   d(μ, μ) = 0.

Suppose that the internal stages have been exact for the linear equation (5.1), that is, Yi = exp (iciμ)y0, then the update gives
()
where
()
Accordingly, the quantities
()
are called the phase lag and the dissipation of the update of the method (2.1), respectively. If ϕu(μ, ν) = 𝒪(μq+1), and du(μ, ν) = 𝒪(μp+1), then the update of the method (2.1) is said to be dispersive of order q and dissipative of order p, respectively.
Letting ν = rμ, we obtain the phase lags and dissipations of the four FRK methods derived in Section 4.
  • (i)

     Simos4:

    ()

  • (ii)

    FRK4:

    ()

  • (iii)

    FRK5a:

    ()

  • (iv)

    FRK5b:

    ()

Therefore, when integrating the test equation (5.1), the methods Simos4 and FRK4 are dispersive of order four and dissipative of order five, and FRK5a and FRK5b are dispersive of order six and dissipative of order five. Similar conclusions for their updates can be drawn from the above analysis.

Note that if the update of (2.1) is phase-fitted and amplification-fitted, it must be true that ϕu(μ, μ) = 0 and du(μ, μ) = 0, as is verified above for the two methods FRK4 and FRK5b.

6. Numerical Experiments

In order to examine the effectiveness of the new FRK methods proposed in this paper, we apply them to four test problems. We also employ several highly efficient integrators from the literature for comparison. The numerical methods we choose for experiments are as follow:
  • (i)

    FRK5a: the seven-stage RK method of order five given by (4.17) and (4.20) in Section 4 of this paper;

  • (ii)

    FRK5b: the seven-stage RK method of order five given by (4.17) and (4.28) in Section 4 of this paper;

  • (iii)

    Simos4: the RK method of order four presented in [23], that is, the four-stage FRK method of order four given by (4.1) and (4.12) in Section 4 of this paper;

  • (iv)

    FRK4: the four-stage RK method of order four given by (4.1) and (4.12) in Section 4 of this paper;

  • (v)

    ARK4: the second four-stage adapted RK method of order four given in the Subsection 3.2 of Franco [11];

  • (vi)

    EFRK4: the four-stage exponentially fitted RK method of order four given in [26];

  • (vii)

    RK4: the classical RK method of order four presented in [3] (the prototype method of Simos4 and FRK4);

  • (viii)

    RK5: the classical RK method of order five presented in [3] (the prototype method of FRK5a and FRK5b).

In the figures showing the efficiency of these integrators, the horizontal axis stands for the number of function evaluations required and the vertical axis stands for the digital logarithm of the maximal global error (MGE).

Problem 1. Consider the following orbit problem studied in [27]:

()
This equation is the real part of the “almost” periodic orbit problem as
()
The exact solution to this problem is q(t) = cos (t) + 0.0005tsin(t). We select the fitting frequency ω = 1.0007 and integrate the equation on the interval [0,1000] with step sizes h = 1/2i,   i = 0,1, 2,3. The numerical results are presented in Figure 3(a).

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Efficiency curves of Problem 1 (a) and Problem 2 (b).
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Efficiency curves of Problem 1 (a) and Problem 2 (b).

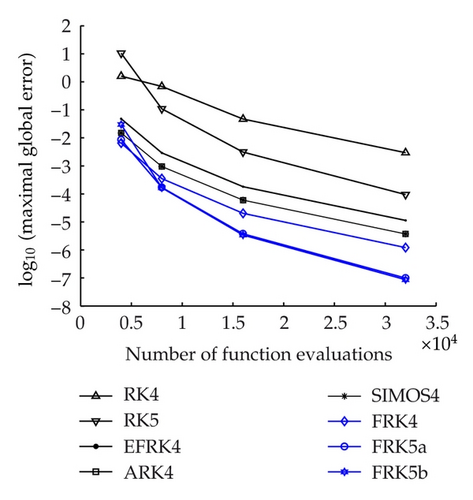
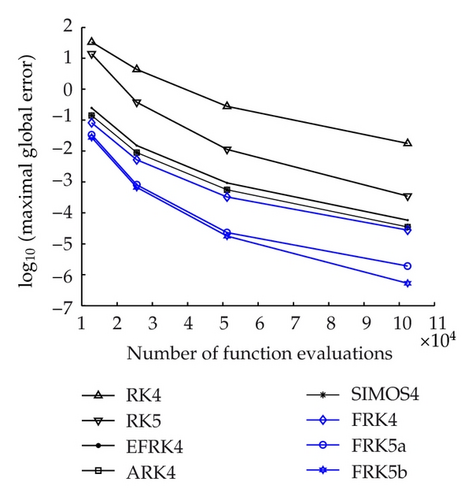
Problem 2. Consider the following linear problem studied in [9]:

()
The exact solution to this problem is y(t) = cos (ωt) + sin(ωt) + sin(t). In this experiment, we take the parameter ω = 20 and integrate the equation on the interval [0,100] with the step sizes h = 1/(8i),   i = 2,3, 4,5. The numerical results are presented in Figure 3(b).

Problem 3. Consider the prey-predator system in ecology (see [28]) as

()
where u(t) is the number of prey at time t, v(t) is the number of predators at time t, and are first derivatives with respect to time, and α, β, γ, δ are positive constants. For given initial values u(0) = u0, v(0) = v0, the system has unique solution, but analytical solution is not available. However, the system has an invariant I(u, v) = δln u + αln u − γu − βv in the sense that (d/dt)I(u(t), v(t)) ≡ 0. The efficient of the methods will be tested by measuring the error growth of the invariant I(u(t), v(t)) against the number of function evaluations required.

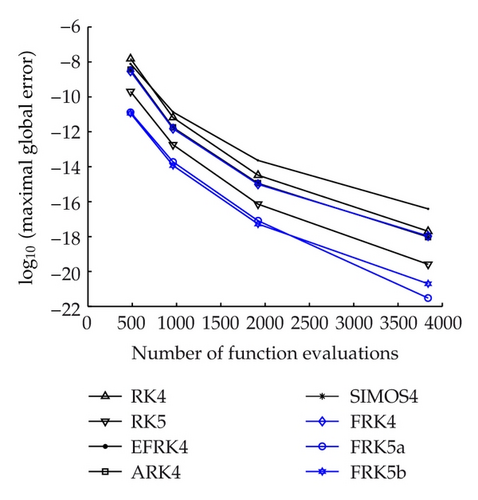
In this experiment, we take the values of parameters α = 2, β = γ = δ = 1 and take initial data u0 = 1.6,   v0 = 2.2. We select the fitting frequency ω = 1.0075 and integrate the equation on the interval [0,30] with step sizes h = 1/2i,   i = 2,3, 4,5. The numerical results are presented in Figure 4(a).

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Efficiency curves of Problem 3 (a) and Problem 4 (b).
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Efficiency curves of Problem 3 (a) and Problem 4 (b).

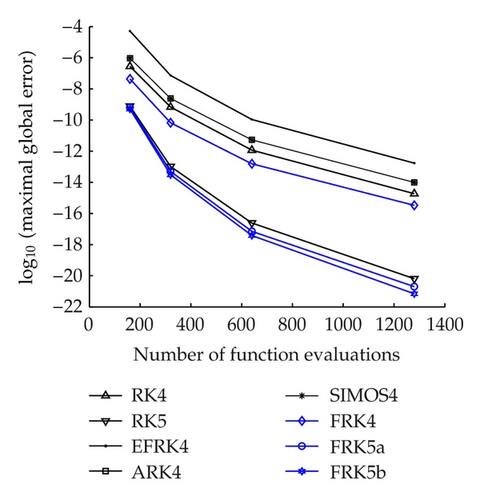
Problem 4. We consider the following two-gene regulatory system without self-regulation (see Widder et al. [29] and Polynikis et al. [30]):

()
where i = 1,2, ri is the concentration of mRNA Ri produced by gene Gi, pi is the concentration of protein Pi, mi is the maximal transcription rate of Gi, ki is the translation rate of Ri, γi is the degradation rate of Ri, and δi is the degradation rate of Pi. The two functions
()
are the Hill functions of activation and repression, respectively. The parameters n1, n2 are the Hill coefficients, θ1, θ2 are the expression thresholds.

The solution of the system is an equilibrium of the system (6.5). Now we take the values of parameters as follows:

()
For any initial point (r1(0), r2(0), p1(0), p2(0)) near the equilibrium, the system (6.5) has a stable limit cycle.

In this experiment, we take initial data (0.6,0.8,0.4,0.6) and select the fitting frequency ω = 1.48. The problem is integrated on the interval [0,20] with step sizes h = 1/2i,   i = 1,2, 3,4. The numerical results are presented in Figure 4(b).

It can be seen from Figures 3 and 4 that the FRK methods are more efficient than their prototype RK methods and are more efficient than the other frequency depending methods of the same algebraic order.

7. Conclusions

In this paper, classical Runge-Kutta methods are adapted to the time integration of initial value problems of first order differential equations whose solutions have oscillatory properties. The newly developed phase-fitted and amplification-fitted Runge-Kutta methods (FRK) adopt functions of the product ν = ωh of the fitting frequency ω and the step size h as weight coefficients in the update. FRK methods have zero dispersion error and zero dissipation error when applied to the standard linear oscillator y′ = iωy. That is to say, they preserve initial phase and amplification with time. Therefore, FRK integrators are a kind of integrators which preserve the oscillation structure of the problem.

As the fitting frequency tends to zero, FRK methods reduce to their classical prototypes methods. Furthermore, an FRK method has the same algebraic order and the same error constant with its prototypes method. Numerical experiments illustrate the high efficiency of FRK methods compared with their prototype methods and some other frequency depending methods like exponentially fitted RK type methods.

Theorem 3.3 gives a pair of sufficient conditions for modified RK type methods to be phase-fitted and amplification-fitted. The coefficients of the methods Simos4 and FRK5a are obtained with these conditions combined with an appropriate number of order conditions associated to low order trees. Since the updates of the methods FRK4 and FRK5b are also phase-fitted and amplification-fitted, they may be more efficient than those methods whose updates do not have this property.

In practical computations of oscillatory problems, the true frequency is, in general, not available. The fitting frequency contained in an FRK method is just an estimate of the true frequency. Sometimes the choice of the value of the fitting frequency ω for the FRK method affects their effectiveness to some extent. For instance, in the experiment of Problem 1, we find that the value of ω = 1.0007 is superior to the usual choice ω = 1. For approaches to estimating principal frequencies we refer to the papers [31–36].

This paper provides a convenient approach to constructing FRK methods. Other effective approaches are possible. For example, the fitting frequency can also be incorporated into internal coefficients aij or into nodes ci just as in [12]. Or frequency-dependent coefficients may be introduced to the terms yn in the modified (2.1) as in [26]. In these cases, the internal stages can also be made phase-fitted and amplification-fitted.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant no. 11171155), the Fundamental Research Fund for the Central Universities (Grants no. Y0201100265 and KYZ201125), and the Research Fund for the Doctoral Program of Higher Education (Grant no. 20100091110033). The authors would like to thank the referees for their valuable comments and suggestions.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.