Discrete Dynamics in Nature and Society
Volume 2012, Issue 1 201678
Research Article
Open Access

Local Polynomial Regression Solution for Partial Differential Equations with Initial and Boundary Values

Liyun Su, 

Corresponding Author

Liyun Su

School of Mathematics and Statistics, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author
Tianshun Yan, 

Tianshun Yan

School of Mathematics and Statistics, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author
Yanyong Zhao, 

Yanyong Zhao

School of Mathematics and Statistics, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author
Fenglan Li, 

Fenglan Li

Institute of Library, Chongqing University of Technology, Chongqing 400054, China cqut.edu.cn

Search for more papers by this author
First published: 13 September 2012
https://doi.org/10.1155/2012/201678
Citations: 2
Academic Editor: Leonid Shaikhet

Abstract

Local polynomial regression (LPR) is applied to solve the partial differential equations (PDEs). Usually, the solutions of the problems are separation of variables and eigenfunction expansion methods, so we are rarely able to find analytical solutions. Consequently, we must try to find numerical solutions. In this paper, two test problems are considered for the numerical illustration of the method. Comparisons are made between the exact solutions and the results of the LPR. The results of applying this theory to the PDEs reveal that LPR method possesses very high accuracy, adaptability, and efficiency; more importantly, numerical illustrations indicate that the new method is much more efficient than B-splines and AGE methods derived for the same purpose.

1. Introduction

There are some effective and convenient numerical methods for partial differential equations problems with initial and boundary values;for example, the radial basis functions are used to solve two-dimensional sine-Gordon equation in [1], a family of second-order methods are used to solve variable coefficient fourth-order parabolic partial differential equations in [2], and fifth-degree B-spline solution is available for a fourth-order parabolic partial differential equations in [3]. Recently, H. Caglar and N. Caglar [4] have used local polynomial regression (LPR) method for the numerical solution of fifth-order boundary value problems [4]. Moreover, they manage to solve linear Fredholm and Volterra integral equations by using LPR method [5]. Consequently, we can consider LPR method is applied to some PDEs with initial and boundary values, and numerical results demonstrate that local polynomial fitting method is more accurate, simple, and efficient. First, we consider the numerical approximation for the simple nonhomogeneous PDE with initial values with the use of local polynomial regression:
(1.1)

2. Bivariate Local Polynomial Regression

Bivariate local polynomial regression is an attractive method both from theoretical and practical point of view. Multivariate local polynomial method has a small mean squared error compared with the Nadaraya-Watson estimator which leads to an undesirable form of the bias and the Gasser-Muller estimator which has to pay a price in variance when dealing with a random design model. Multivariate local polynomial fitting also has other advantages. The method adapts to various types of designs such as random and fixed designs and highly clustered and nearly uniform designs. Furthermore, there is an absence of boundary effects: the bias at the boundary stays automatically of the same order as the interior, without the use of specific boundary kernels. The local polynomial approximation approach is appealing on general scientific grounds; the least squares principle to be applied opens the way to a wealth of statistical knowledge and thus easy generalizations. All the above-mentioned assertions or advantages can be found in literatures [6–10]. The basic idea of multivariate local polynomial regression is also proposed in [11–14]. In this section, we briefly outline the idea of the extension of bivariate local polynomial fitting to bivariate regression.

Suppose that the state vector at point T is XT:
(2.1)
Our purpose is to obtain the estimation . In this paper, we use the dth order multivariate local polynomial fi(X) to predict the value of the fixed-point XT. The polynomial function can be described as
(2.2)
where
(2.3)
d is the order of the expansion:
(2.4)
In the bivariate regression method, the change of XT on the attractor is assumed to be the same as those of nearby points, according to the distance order. Using A pairs of , for which the values are already known, the coefficients of fi are determined by minimizing
(2.5)
For the weighted least squared problem, when XTWX is inverse, the solution can be described by
(2.6)
where
(2.7)
and X is the A × S  (S = ∑0≤|j|≤d |j|/j!),
(2.8)
Then we can get the estimation :
(2.9)
where Ei = (1,0, 0, …, 0) 1×S. There are several important issues about the bandwidth, the order of multivariate local polynomial function, and the kernel function which have to be discussed.

2.1. Parameters Estimations and Selections

There are many of the embedding dimensions algorithms [15, 16]. In univariate series , a popular method that is used for finding the embedding dimensions mi is the so-called false nearest-neighbor method [17, 18]. Here, we apply this method to the bivariate case.

For the multivariate local polynomial estimator, there are three important problems which have significant influence on the prediction accuracy and computational complexity. First of all, there is the choice of the bandwidth matrix, which plays a rather crucial role. The bandwidth matrix H is taken to be a diagonal matrix. For simplification, the bandwidth matrix is designed into H = hI2, where I2 is a unit matrix of two orders. In theory, there exists an optimal bandwidth hopt in the meaning of mean squared error, such that
(2.10)

But the optimal bandwidth cannot be solved directly. So we discuss how to get the asymptotically optimal bandwidth. We make use of searching method to select bandwidth. When the bandwidth h varies from small to big, compared with the values of the objective function, we can choose the smallest bandwidth to ensure the minimum value of the objective function. So the smallest bandwidth is the optimal bandwidth.

Given hl = Clhmin , where hmin  is minimum, Cl is efficient of expansion. We search the bandwidth h to ensure the objective function value of minimum in district [hmin , hmax ], where the objective function stands for the mean square error (MSE).

First, we assume h = hmin  and then increase h by making use of efficient of expansion Cl. When h > hmax  stops, the minimum h is the optimal bandwidth if EMS(h) obtains the minimum..  EMS(h) can be taken place of
(2.11)
where I is the number predicted. In this paper, we choose
(2.12)
where hm = max ∥Xi − Xj∥,Cl = 1.1. Compared to other methods, this method is more convenient.
In order to get closer to the ideal optimal bandwidth, we search once again by narrowing the interval on the basis of the previous searching process. Suppose j is the bandwidth which makes optimal in the above searching process. Now, small interval is divided into n equal intervals again. Suppose
(2.13)
Among n − 1 bandwidth, the bandwidth that makes eMS minimized is the optimal bandwidth.

Another issue in multivariate local polynomial fitting is the choice of the order of the polynomial. Since the modeling bias is primarily controlled by the bandwidth, this issue is less crucial, however. For a given bandwidth h, a large value of d would expectedly reduce the modeling bias but would cause a large variance and a considerable computational cost. Since the bandwidth is used to control the modeling complexity, and due to the sparsity of local data in multidimensional space, a higher-order polynomial is rarely used. So, we apply the local quadratic regression to fit the model (i.e., p = 2,3). The third issue is the selection of the kernel function. In this paper, we choose the optimal spherical Epanechnikov kernel function [6, 7] which minimizes the asymptotic mean square error (MSE) of the resulting multivariate local polynomial estimators, as our kernel function.

3. LPR Solutions for PDE

For the following nonhomogeneous PDE with boundary values:
(3.1)
Suppose XT = (xT, tT), so our purpose is to obtain estimation given n2 pairs of points , where , , ; then we can get
(3.2)
that is described by
(3.3)
Consequently, the corresponding minimization function is
(3.4)
In order to find expression of X, we need to find the elements of X at first.
Since binary function’s p-order Taylor expansion has (p2 + 3p + 2)/2 items, then we can get expressions (3.5), (3.6), and (3.7):
(3.5)
where X is n2 × (p + 1)(p + 2)/2 matrix:
(3.6)
(3.7)
Substitute (3.6) and (3.7) into
(3.8)
Now, we can get the estimation ,
(3.9)
where Ei = (1,0, 0, …, 0) 1×S  (S = ∑0≤|j|≤d  | j | /j!).

4. Numerical Illustrations and Discussions

In this section we consider the numerical results obtained by the schemes discussed previously by applying them to the following second-order and fourth-order initial boundary value problems. All computations are carried out using MATLAB 7.0.

Furthermore, in order to evaluate the accuracy and effectiveness, we apply the following indices, namely, the mean squared prediction error (MSE):
(4.1)
and the absolute error
(4.2)

Example 4.1. First, we consider the following second-order nonhomogeneous PDEs:

(4.3)

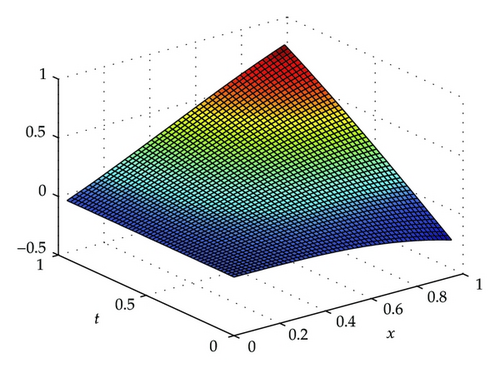
The exact solution for problems (4.3) is u(x, t) = tsin x. We solve Example 4.1 with n = 20,30,50 by choosing p = 3,4 and various values of parameters Hi presented in Table 1. The errors in the solutions are computed by our method (3.9). In Table 1, p = 3,4. Given n = 20, p = 3,4, it is found that the magnitude of MSE is between 10 to the power of −3 and 10 to the power of −4. Given n = 30, p = 3,4, it can be seen that the magnitude of MSE is between 10 to the power of −4 and 10 to the power of −7. However, by setting up n = 50, p = 3,4, it is obvious that the magnitude of MSE is between 10 to the power of −5 and 10 to the power of −8. We conclude that MSE decreases with the increase of the value of n the value of order p has no much influence on MSE for a large value of β. Consider parameter H; specifically, MSEs get up to minimum for p = 3, n = 20 when H3 = 1/25, for p = 3, n = 30 when H4 = 3/100, for p = 3, n = 50 when H5 = 1/40. We can find that the optimal bandwidth H locates in district [0.025I2, 0.04I2] by using method (2.12)-(2.13) for n = 20, 30, 50. For p = 4, there exists the same situation with p = 3. Here, I2 is a unit matrix of two orders. The fitting figure is depicted in Figure 1 using matlab 7.0.

Table 1. Mean square errors (MSEs) with different values of p, H given n = 20, 30, 50 in Example 4.1, I2: unit matrix of two orders.
Parameters (p,  Hi) MSE (n = 20) MSE (n = 30) MSE (n = 50)
p  = 3, H1  =  (11 /100)  I2 8.5223  ×  10−3  6.5223  ×  10−4 6.3252  ×  10−5
p = 3, H2  =  (2 /25) I2 3.0309  ×  10−3  4.2541  ×  10−4 9.7206  ×  10−6
p = 3, H3  =  (1 /25) I2 1.1268  ×  10−4 8.3418  ×  10−5 6.0211  ×  10−6
p = 3, H4  =  (3 /100) I2 5.3082  ×  10−4 5.2087  ×  10−5 1.1528  ×  10−6
p = 3, H5  =  (1/40) I2 6.9123  ×  10−4 5.6021  ×  10−5 3.9107  × 10−7
p = 3, H6  =  (1 /75) I2 3.3082  ×  10−3 2.8339  ×  10−5 1.8815  ×  10−6
  
p = 4, H1  =  (11 /100) I2 4.1004  ×  10−4 6.6033  ×  10−6 5.8311  ×  10−7
p = 4, H2  =  (2 /25) I2 1.8791  ×  10−4 2.2416  ×  10−6 3.4525  ×  10−7
p = 4, H3  =  (1 /25) I2 6.6568  ×  10−5 9.5066  ×  10−7 3.0373  ×  10−7
p = 4, H4  =  (3 /100) I2 9.0893  ×  10−5 7.3137  ×  10−6 9.7815  ×  10−8
p = 4, H5  =  (1/40) I2 5.9803  × 10−4 5.6401  × 10−6 4.1266  ×  10−8
p = 4, H6  =  (1 /75) I2 5.7911  ×  10−4 7.3452  ×  10−6 2.3098  ×  10−7
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
LPR of Example 4.1.

Example 4.2. Next we consider the following fourth-order nonhomogeneous PDEs:

(4.4)
with the initial conditions,
(4.5)
and the boundary conditions at x = 0 and x = 1 of the form
(4.6)

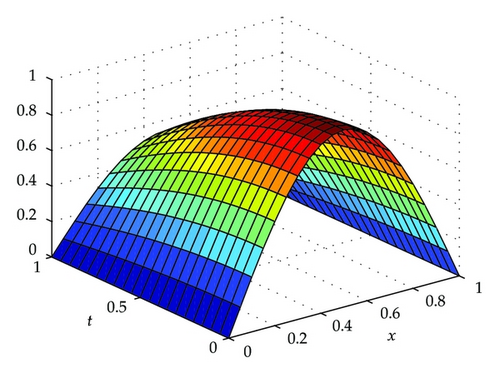
The exact solution for problems (4.4), (4.5), and (4.6) is u(x, t) = sin πxcos t. This problem has been solved by several authors [19, 20]. Here, we try to solve Example 4.2 with n = 30,50 by choosing p = 3,4 and various values of parameters H presented in Table 2. The errors in the solutions are computed by our method (3.9); the splines method for three kinds of values of p, q, s, σ, h in [19], and the AGE method for two kinds of values of its parameters in [20] have been presented in Table 2. In Table 1, p = 3,4. Given n = 30, it is found that the magnitude of MSE is between 10 to the power of −4 and 10 to the power of −6 for p = 3, between 10 to the power of −6 and 10 to the power of −8 for p = 4. We can see the value of order p has a little influence on MSE. Consider parameter H; specifically, MSEs get up to minimum for p = 3, n = 20 when H3 = 1/25, for p = 3, n = 30 when H4 = 3/100, for p = 3, n = 50 when H5 = 1/40. Similar to Example 4.1, we can also acknowledge the optimal bandwidth H exists in district [0.025I2, 0.03I2] by using method (2.12)-(2.13), for n = 30 and n = 50 given p = 4,5. Furthermore, we have tabulated the absolute errors (AEs) at x = 0.10,0.20 for different combination of parameters p, H for n = 30 and n = 50, respectively. Given n = 30, p = 4, 5, the magnitude of AE is between 10 to the power of −3 and 10 to the power of −6 at point x = 0.1, and given n = 50, p = 4, 5, the magnitude of AE is between 10 to the power of −5 and 10 to the power of −7 at point x = 0.2. Here, I2 is a unit matrix of two orders. The fitting figure is also illustrated in Figure 2 using matlab 7.0.

Table 2. Mean square errors (MSEs) with different values of p, H given n  =  30 and absolute errors (AE) given n  =  30, 50 in Example 4.2, I2: unit matrix of two orders.
Parameters (h, Hi) MSE (n = 30) AE (x  = 0.10, n = 30) AE (x  = 0.20, n = 50)
p = 4, H1  =  (11 /100) I2, 2.3109  ×  10−4  4.7882  ×  10−3  9.4388  ×  10−5 
p = 4, H2  =  (2 /25) I2, 4.1493  ×  10−4  3.1431  ×  10−3 4.6412  ×  10−5 
p = 4, H3  =  (1 /25) I2, 3.8981  ×  10−5  6.9083  ×  10−4  1.0603  ×  10−5 
p = 4, H4  =  (3 /100) I2, 9.2391  ×  10−6  1.1425  ×  10−4  7.5229  ×  10−6 
p = 4, H5  =  (1 /40) I2, 9.0117  ×  10−6  6.8858  ×  10−4  9.1029  ×  10−7 
p = 4, H6  =  (3 /100) I2, 7.3249  × 10−6  9.4551  ×  10−5  2.1002  ×  10−6 
  
p = 5, H1  =  (11 /100) I2, 7.0113  ×  10−7  8.9211  ×  10−5  6.8564  ×  10−6 
p = 5, H2  =  (2 /25) I2, 4.5881  ×  10−7 7.8423  ×  10−5  5.0705  ×  10−6 
p = 5, H3  =  (1 /25) I2, 2.1062  ×  10−7 2.6065  ×  10−5  9.6552  ×  10−7 
p = 5, H4  =  (3 /100) I2, 9.7922  × 10−8  5.8232  ×  10−6 8.2302  ×  10−7 
p = 5, H5  =  (1 /40) I2, 3.8717  ×  10−6 4.2410  ×  10−5  3.0671  × 10−7
p = 5, H6  =  (1/75) I2, 8.9821  ×  10−6 7.9102  ×  10−5  6.3409  ×  10−6 
  
Aziz et al. [19] (p,  q,  s,  σ,  h)   x = 0.10, steps = 10      x = 0.20, steps = 16     
  
(0, 0, 1, 1/4, 1/20) — 1.5000  ×  10−4 5.1000  ×  10−5
(0, 1/6, 2/3, 1/4, 1/20) 1.8000  ×  10−5 8.0000  ×  10−6
(1/144, 5/36, 17/24, 1/4, 1/20) 1.8000  ×  10−5 7.9000  ×  10−6
  
Evans and Yousif [20] — 2.2000  ×  10−4 4.1000  ×   10−4
2.5000  ×  10−5 4.7000  ×   10−5
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
LPR of Example 4.2.

5. Conclusions

In this paper, LPR method can be applied for the numerical solution of some kinds of PDEs. We can also see that LPR method has been exploited to solve fifth-order boundary value problems [4] and Fredholm and Volterra integral equations [5] whose maximum absolute errors are very small and calculation processes are simple and feasible. Compared with the splines method [19] and the AGE method [20], LPR method converges to solutions with fewer number of nodes, and the maximum absolute errors are a little smaller. Moreover, it is more flexible to resolve problems just only adjusting parameters h, p. However, LPR methods have shortcomings which need more computation time compared with splines method [19] for the same problems, which can be tried to discuss and resolve afterward. In any case, it is more important that we can conclude LPR solution is a powerful tool for numerical solutions of differential equations with initial and boundary values.

Acknowledgment

This work was supported by Natural Science Foundation Projects of CQ CSTC of China (CSTC2010BB2310, CSTC2011jjA40033, CSTC2012jjA00037) and Chongqing CMEC Foundations of China (KJ080614, KJ120829).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.