Advances in Meteorology
Volume 2012, Issue 1 178623
Research Article
Open Access

Wind Velocity Vertical Extrapolation by Extended Power Law

Zekai Şen, 

Zekai Şen

Hydraulics Division, Civil Engineering Faculty, Istanbul Technical University, Maslak, 34469 Istanbul, Turkey itu.edu.tr

Search for more papers by this author
Abdüsselam Altunkaynak, 

Abdüsselam Altunkaynak

Hydraulics Division, Civil Engineering Faculty, Istanbul Technical University, Maslak, 34469 Istanbul, Turkey itu.edu.tr

Search for more papers by this author
Tarkan Erdik, 

Corresponding Author

Tarkan Erdik

Hydraulics Division, Civil Engineering Faculty, Istanbul Technical University, Maslak, 34469 Istanbul, Turkey itu.edu.tr

Search for more papers by this author
First published: 18 November 2012
https://doi.org/10.1155/2012/178623
Citations: 32
Academic Editor: Harry D. Kambezidis

Abstract

Wind energy gains more attention day by day as one of the clean renewable energy resources. We predicted wind speed vertical extrapolation by using extended power law. In this study, an extended vertical wind velocity extrapolation formulation is derived on the basis of perturbation theory by considering power law and Weibull wind speed probability distribution function. In the proposed methodology not only the mean values of the wind speeds at different elevations but also their standard deviations and the cross-correlation coefficient between different elevations are taken into consideration. The application of the presented methodology is performed for wind speed measurements at Karaburun/Istanbul, Turkey. At this location, hourly wind speed measurements are available for three different heights above the earth surface.

1. Introduction

Wind energy, as one of the main renewable energy sources in the world, attracts attention in many countries as the efficient turbine technology develops. Wind speed extrapolation might be regarded as one of the most critical uncertainty factor affecting the wind power assessment, when considering the increasing size of modern multi-MW wind turbines. If the wind speed measurements at heights relevant to wind energy exploitation lacks, it is often necessary to extrapolate observed wind speeds from the available heights to turbine hub height [1], which causes some critical errors between estimated and actual energy output, if the wind shear coefficient, n, cannot be determined correctly. The difference between the predicted and observed wind energy production might be up to 40%, due to turbulence effects, time interval of wind data measurement, and the extrapolation of the data from reference height to hub heights [2].

In the literature, the wind shear coefficient is generally approximated between 0.14 and 0.2. However, in real situations, a wind shear coefficient is not constant and depends on numerous factors, including atmospheric conditions, temperature, pressure, humidity, time of day, seasons of the year, the mean wind speed, direction, and nature of terrain [3–6]. Table 1 demonstrates the various wind shear coefficients for different types of topography and geography [3].

Table 1. Wind shear coefficient of various terrains [3].
Terrain type  
Lake, ocean, and smooth-hard ground 0.1
Foot-high grass on level ground 0.15
Tall crops, hedges, and shrubs 0.2
Wooded country with many trees 0.25
Small town with some trees and shrubs 0.3
City area with tall buildings 0.4

According to the calculations of wind resource analysis program (WRAP) report, in 39 different regions, out of 7082 different wind shear coefficients, 7.3% are distributed between 0 and 0.14 and 91.9% above 0.14, while 0.8% are calculated as negative [7], due to the measurements error.

Different methods have been developed to analyze wind speed profiles, such as power, logarithmic, and loglinear laws [8]. Besides, in the literature various studies are conducted in order to estimate wind shear coefficient in the power law only if surface data is available at hand [9–11].

The wind speed undergoes repeated changes, as a result of which the roughness and friction coefficients also change depending on landscape features, the time of the day, the temperature, height and wind direction. The uncertainty is inhereted in the wind speed data and its extrapolation to the hub height should be considered carefully and preciously [12]. Moreover, this uncertainty is exacerbated in the offshore environment by the inclusion of the dynamic surface [13]. Therefore, the mean wind speed profile of the logarithmic type is developed by applying a stability correction for offshore sites [14].

It is crucial point for energy investors to accurately predict the average wind speed at different wind turbine hub heights and make realistic feasibility projects for these heights. In this study, a simple but effective methodology on the basis of the perturbation theory is presented in order to derive an extended power law for the vertical wind speed extrapolation and then the Weibull probability distribution function (pdf) parameters. It is observed that on the contrary to the classical approach not only the means of wind speeds are at different elevations, but also the standard deviations and the cross-correlation coefficient should be taken into consideration, if the wind speeds at different elevations are not independent from each other.

2. Power Law

This law is the simplest way for estimating the wind speed at a wind generator hub elevation from measurements at a reference level. In general, the power law expression is given as,
()
where terms in the brackets are the velocity and elevation ratios, V2 > V1 and Z2/Z1, respectively. Furthermore, V2 > V1 and Z2 > Z1; and n is the exponent of the power law, which is a complex function of the local climatology, topography, surface roughness, environmental conditions, meteorological lapse rate, and weather stability. It is clear that the effects of all these factors are embedded in the wind velocity time records, and consequently, their total reflections are also expected in the value of the exponent, n. Therefore, one tends to think whether there is a way of obtaining the estimation of this exponent from the wind speed time series. Power laws are used almost exclusively without any generally accepted methodology. Most often, only the arithmetic averages of the wind speed at two elevations are considered in the numerical calculation of the exponent. Logically, other than the mean values, standard deviations and cross-correlation coefficient should enter the calculations, because these additional parameters arise as a result of instability, roughness, and so forth. Provided that there are wind speed records at two or more elevations, the following approach provides an objective solution.

3. Extended Power Law

In (1), the only random variable that represents the weather situation is the wind speeds, which can be written in terms of the averages and perturbation terms about their averages that render (1) to
()
where and are the perturbation terms with averages equal to zero, . This last expression can be rewritten simply as
()
This expression is referred to as the extended power law in this paper. The third bracket on the right-hand side corresponds to a geometric series, which can be expressed by the Binomial expansion as
()
This expression can still be simplified after the expansion of the second and third brackets on the right-hand side and then by considering the second-order term approximately yields
()
After taking the arithmetic averages of both sides and then considering that the odd order power term averages are equal to zero, (5) yields to
()
By definition , exactly. In fact, for symmetrical (i.e., Gaussian) perturbation terms, the odd number arithmetic averages such as are also equal to zero approximately by definition.
In (6), the common arithmetic average of the perturbation multiplication, , at two different elevations is equal to the covariance of the perturbations. This can be written in terms of the standard deviations and and cross-correlation, r12, multiplication as . The second-order perturbation term average, , is equivalent to the variance of the perturbation term as . The substitution of these last two expressions into (6) leads to
()
where and are the standard deviations and r12 is the cross-correlation coefficient between the wind speed time series at two elevations. In practice, most often the cross-correlation term in (7) is overlooked by assuming that there are no random fluctuations around the mean speed values which bring the implication that the standard deviations are equal to zero. These assumptions are not valid because in an actual weather, there are always fluctuations in the wind speed records as in Figure 1. By definition in statistics, the ratio of standard deviation to the arithmetic mean is the coefficient of variation, and hence (7) can be rewritten in parameterized form as,
()
Herein, and are the coefficients of variation for the wind speed records, V1 and V2, at two different elevations, respectively.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Karaburun wind speed records at different levels.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Karaburun wind speed records at different levels.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
Karaburun wind speed records at different levels.

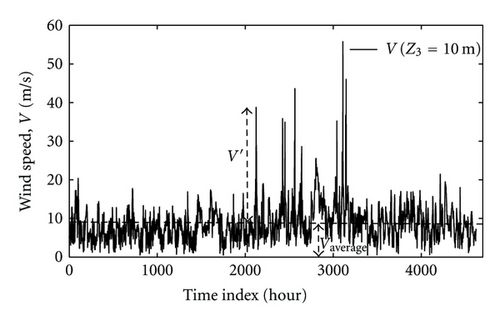
4. Weibull Distribution Parameter Extrapolation

Extrapolation of wind speed data to standard elevations poses a rather subjective approach based on the mean wind velocity only. Unreliability in such extrapolations is reflected in the subsequent wind energy, E, calculations through the classical formulation
()
where ρ is the standard atmosphere air density which is equal to 1.226 gr/cm3 at 25°C, and V is the wind speed. Most often the wind speed at a meteorology station is measured along a tower at different elevations, and it is desired to be able to find the wind profile at this station for further wind loadings or energy calculations. Some researchers have employed the Weibull pdf for empirical wind speed relative frequency distribution (histogram), and a set of formulas are derived for the extrapolation of the Weibull pdf parameters [15–18]. In general, two-parameter Weibull pdf of wind speed, P(V), is given as,
()
where k is a dimensionless shape parameter, and c is a scale parameter with the speed dimension. In many applications, the basic Weibull pdf statistical properties are the expectation, E(V), variance, Var (V), and the mth order moment E(Vm) around the origin which are explicitly available as [19]
()
()
()
respectively.

It is the purpose of this paper to present detailed extrapolation formulations for the Weibull pdf parameters on the basis of perturbation approach and power law of vertical wind velocity variation.

The two-parameter Weibull pdf has the average and standard deviation as in (11) and (12); and by definition their ratio gives the coefficient of variation as
()
The k value can best be estimated by using the approximate relationship for (14) as given by Justus and Mikhail [17], that is:
()
and (11) yields the scale parameter as
()
The substitution of these last two expressions for two elevations with labels 1 and 2 into (8) leads after some algebra to
()
By taking the logarithms of both sides, give
()
Hence, once the Weibull pdf parameters, c and k, are determined the power exponent can be calculated provided that the cross-correlation coefficient, r12 is found from the available wind speed time series data. It must be noticed that this last expression reduces to the classical counterpart in (1) after the substitution of k2 = 0. Therefore, this expression can be written as
()

5. Application

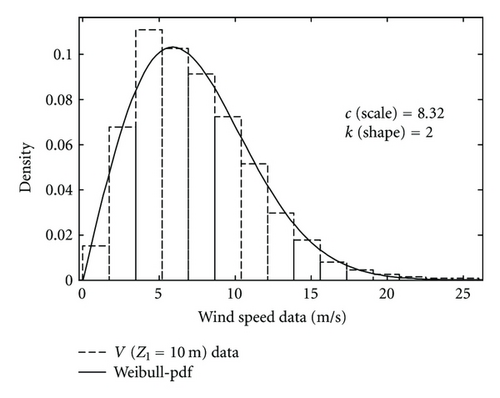
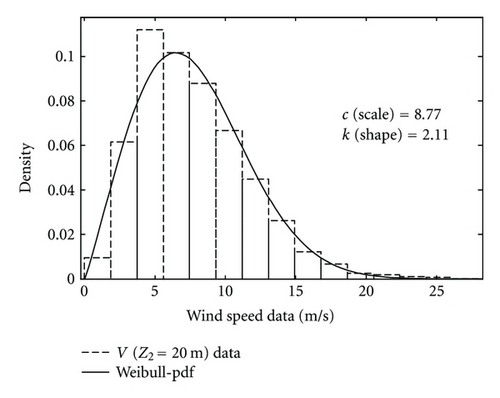
In this paper, wind speed data from the Karaburun wind station in Istanbul, Turkey are used, and this station is located at latitude 41.338′ N and longitude 28.677′ E (Figure 2). At this location hourly, wind speed measurements are available at three different heights (10 m, 20 m, and 30 m) above the earth surface. The average wind speed, the standard deviation, and the coefficient of variation for each height are given in Table 2. Wind speed data measurement empirical relative frequency distribution functions (histograms) at 10 m, 20 m, and 30 m are given together with the theoretically fitted Weibull pdf’s in Figure 3 for each height. A good fit between the empirical and theoretical counterparts at different heights are obtained through the Kolmogorov-Smirnov test at significance level of 5%. Table 1 presents the Weibull pdf parameters, c (scale) and k (shape). The scale parameters are 8.32, 8.77, and 9.54 for heights of 10 m, 20 m, and 30 m, respectively. The shape parameters are determined as 2, 2.11, and 2.06, respectively for the same heights.

Table 2. Wind speed summary statistics of Karaburun for three different heights.

Height

(m)

Mean speed

(m/s)

Standard deviation

(m/s)

 Coefficient of variation Weibull pdf parameters
      c k
10 7.37 3.86 0.52 8.32 2.0
20 7.75 3.88 0.50 8.77 2.11
30 8.44 4.30 0.51 9.54 2.06
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The location of the Karaburun wind station.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Karaburun Weibull pdf’s at different levels.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Karaburun Weibull pdf’s at different levels.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Karaburun Weibull pdf’s at different levels.

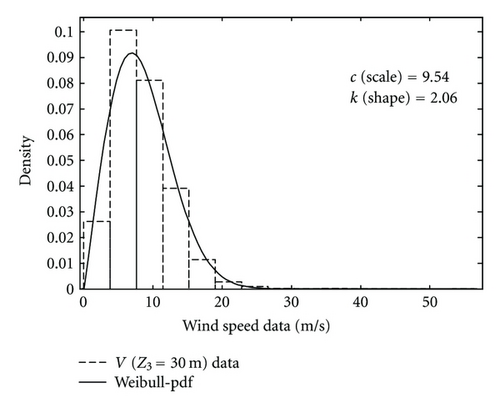
It is clear from this table that as the height increases, the mean speed and standard deviation increase as expected. Coefficient of variation varies with different heights as in Table 2. This shows also that the closer the height to the earth surface, the greater is the instability of the air. The power law exponent, n, calculation between any two heights are found from (18) and classically from (19); and they are presented in Table 3.

Table 3. Exponent calculations both classical and extended power law.

Height

(m)

Classical

(19)

Extended

(18)
10–20 0.0760 0.0935
20–30 0.2076 0.1608
10–30 0.1245 0.1172
  
Average 0.1360 0.1238

For both classical and Weibull pdf approaches the greatest value lies between 20 m and 30 m, whereas the lowest value is between 10 m and 20 m. For all levels, the average values are 0.1360 and 0.1238 for classical and extended power laws, respectively.

6. Conclusions

A simple methodology on the basis of the perturbation theory is presented in order to derive an extended power law for the vertical wind speed extrapolation and then the Weibull probability distribution parameters. It is observed that on the contrary to the classical approach not only the means of wind speeds are at different elevations, but also the standard deviations and the cross-correlation coefficient should be taken into consideration, if the wind speeds at different elevations are not independent from each other. Otherwise, consideration of the classical power law in the calculations embodies the assumption that there are no fluctuations in the wind speed time series around their respective mean values. The necessary formulations for the Weibull distribution function wind speed parameter extrapolations are presented in this paper. The application of the developed methodology is presented for Karaburun, Istanbul, near the Black Sea coast wind speed measurement station data at three different levels.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.