Volume 2012, Issue 1 153542

Research Article

Open Access

Generalized Projective Synchronization between Two Different Neural Networks with Mixed Time Delays

Xuefei Wu,

Xuefei Wu

College of Information and Engineering, Shenzhen University, Shenzhen 518060, China szu.edu.cn

School of Computer Engineering, Shenzhen Polytechnic, Shenzhen 518055, China szpt.edu.cn

Search for more papers by this author

Chen Xu,

Corresponding Author

Chen Xu

[email protected]

College of Mathematics and Computational Science, Shenzhen University, Shenzhen 518060, China szu.edu.cn

Search for more papers by this author

Jianwen Feng,

Jianwen Feng

College of Mathematics and Computational Science, Shenzhen University, Shenzhen 518060, China szu.edu.cn

Search for more papers by this author

Yi Zhao,

Yi Zhao

College of Mathematics and Computational Science, Shenzhen University, Shenzhen 518060, China szu.edu.cn

Search for more papers by this author

Xuan Zhou,

Xuan Zhou

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Xuefei Wu,

Xuefei Wu

College of Information and Engineering, Shenzhen University, Shenzhen 518060, China szu.edu.cn

School of Computer Engineering, Shenzhen Polytechnic, Shenzhen 518055, China szpt.edu.cn

Search for more papers by this author

Chen Xu,

Corresponding Author

Chen Xu

[email protected]

College of Mathematics and Computational Science, Shenzhen University, Shenzhen 518060, China szu.edu.cn

Search for more papers by this author

Jianwen Feng,

Jianwen Feng

College of Mathematics and Computational Science, Shenzhen University, Shenzhen 518060, China szu.edu.cn

Search for more papers by this author

Yi Zhao,

Yi Zhao

College of Mathematics and Computational Science, Shenzhen University, Shenzhen 518060, China szu.edu.cn

Search for more papers by this author

Xuan Zhou,

Xuan Zhou

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

First published: 27 May 2012

https://doi.org/10.1155/2012/153542

Citations: 5

Academic Editor: Taher S. Hassan

Share a link

Email
Wechat
Bluesky

Abstract

The generalized projective synchronization (GPS) between two different neural networks with nonlinear coupling and mixed time delays is considered. Several kinds of nonlinear feedback controllers are designed to achieve GPS between two different such neural networks. Some results for GPS of these neural networks are proved theoretically by using the Lyapunov stability theory and the LaSalle invariance principle. Moreover, by comparison, we determine an optimal nonlinear controller from several ones and provide an adaptive update law for it. Computer simulations are provided to show the effectiveness and feasibility of the proposed methods.

1. Introduction

Over the past two decades, the investigation on the synchronization of complex networks has attracted a great deal of attention due to its potential applications in various fields, such as physics, mathematics, secure communication, engineering, automatic control, biology, and sociology [1–9]. In the literature, there are many widely studied synchronization patterns, which define the correlated in-time behaviors among the nodes in a dynamical network, for example, complete synchronization [10–12], lag synchronization [13–15], anti-synchronization [16–18], phase synchronization [19–21], projective synchronization [22–32], and so on. Projective synchronization reflects a kind of proportionality between the synchronized states, so it is an interesting research topic and has many applications. For instance, if this proportional feature is applied to M-nary digital communication, the communication speed can be accelerated substantially. In view of this merit, many researchers throw themselves into generalized projective synchronization.

Recent years have witnessed many written achievements on projective synchronization between two identical complex dynamical networks [22–30]. We introduce three typical references here. In [28], Chen et al. studied projective synchronization of time-delayed chaotic systems in a driven-response complex network, where the nodes are not partially linear and the scale factors are different from each other. In [29], Feng et al. investigated projective-anticipating and projective-lag synchronization on complex dynamical networks composed of a large number of interconnected components, in which the dynamics of the nodes of the complex networks were time-delayed chaotic systems without the limitation of the partial linearity. In [30], Wang et al. explored the problem of outer synchronization between two complex networks with the same topological structure and time-varying coupling delay with a new mixed outer synchronization behavior. In addition, a novel nonfragile linear state feedback controller is designed to realize the mixed outer synchronization between two networks and proved analytically by using the Lyapunov-Krasovskii stability theory.

However, in real world, studying the phenomena of synchronizing two different complex networks is closer to reality. The so-called different implies that the drive and response networks have different node dynamics, different number of nodes, or different topological structures. Recently, some related works have come out, such as [31, 32]. In [31], Zheng et al. probed into adaptive projective synchronization between two complex networks with different topological structures, although its systems contained time-varying delays. Some results on topology identification were obtained which can be also seen as a highlight of this paper. In [32], the generalized projective synchronization with the above three differences was investigated based on the LaSalle invariance principle. However, the model of complex network only has linear coupling and coupling time delay.

Due to the finite information transmission and processing speeds among the units, the connection delays in realistic modeling of many large networks with communication must be taken into account. Therefore, it is important to study the effect of time delay in synchronization of coupled systems. Usually, time delay involves two parts. One is the delay inside the systems, called internal delay. The other is caused by the exchange of information between systems referred to as coupling delay. Moreover, nonlinear functions can display more nature phenomena. Hence, the internal delay and nonlinear functions are introduced into the considered neural networks in this writing. What is more, the nonlinear functions in the drive and response networks are also different. In particular, three comparable nonlinear controllers are presented to realize the GPS based on the LaSalle invariance principle and some basic inequalities. On the contrary, an optimal nonlinear controller is produced eventually. In the last theorem, we use an adaptive control technique for the optimal nonlinear controller in order to make the feedback control gain small enough.

Notation. Throughout this paper, Rⁿ and R^m×n denote n-dimensional Euclidean space and the set of m × n real matrices, respectively. λ_min(A) represents the smallest eigenvalue of a symmetric matrix A. ⊗ is the Kronecker product. The superscript T of x^T or A^T denotes the transpose of the vector x ∈ Rⁿ or the matrix A ∈ R^m×n. I_n is identity matrix with n nodes.

2. Model Description and Preliminaries

Consider a general neural network with mixed time delays consisting of N₁ nodes and nonlinear couplings, which is described as follows:

(2.1)

where x_i(t) = (x_i1(t), x_i2(t), …, x_in(t)) ^T ∈ Rⁿ, (i ∈ ℐ₁ = {1,2, …, N₁}) are the state variables of the ith node at time t; C₁ = diag {c₁₁, c₁₂, …, c_1n} is the decay constant matrix with c_1m > 0 (m ∈ {1,2, …, n});

and

are system matrices;

and

are the continuous functions of the neurons; the positive constants τ₁ and τ₂ are internal delay and coupling delay, respectively; Γ₁ and Γ₂ are the inner coupling matrices at time t and t − τ₂, respectively, which describe the way of linking the components in each pair of connected two nodes;

and

are coupling configuration matrices which are not necessarily irreducible and symmetric.

In this paper, the neural network (2.1) is used as the drive network, and the response neural network consisting of N₂ nodes is expressed by

(2.2)

where y_i(t) = (y_i1(t), y_i2(t), …, y_in(t)) ^T ∈ Rⁿ, i ∈ ℐ₂ = {1,2, …, N₂} are the state variables of the ith node at time t. Without loss of generality, we suppose N₁ ≥ N₂ > 0. C₂ = diag {c₂₁, c₂₂, …, c_2n} is the decay constant matrix with c_2m > 0 (m ∈ {1,2, …, n});

and

are system matrices;

and

are the continuous functions of the neurons; τ₁, τ₂, Γ₁, and Γ₂ have the same meaning as those in (2.1).

and

are coupling configuration matrices which are not necessarily irreducible and symmetric either.

Now, two mathematical definitions for the generalized projective synchronization are introduced as follows.

Definition 2.1. If there is a nonzero constant σ such that

(2.3)

the GPS between neural networks (2.1) and (2.2) is said to be achieved. The parameter σ is called a scaling factor.

Definition 2.2. A continuous function f(·) : R → R is said to be the nonnegative-bound function class, denoted as f ∈ NBF(ξ), if there exists a positive scalar ξ, such that

(2.4)

holds for any x, y ∈ R.

The following hypothesis is used throughout the paper.

Assumption 2.3. For activation functions , there exist positive constants θ_i, β_i, μ_i, γ_i, π_i, δ_i (i ∈ {1,2, …, n}), such that , , , .

For better convenience, we denote that

(2.5)

Lemma 2.4 (see [33].)For a matrix B = (b_ij) ∈ R^p×q, denote α(B) = (1/2)max [p, q]max _i,j |b_ij|, then

(2.6)

holds for all x ∈ R^p, y ∈ R^q.

3. GPS between Two Different Neural Networks with Mixed Time Delays

In this section, we will make a study of GPS between two different neural networks with mixed time delays by means of the LaSalle invariance principle; the, Lyapunov direct method, and nonlinear feedback control technique.

Define the synchronization errors between the drive network (2.1) and the response network (2.2) as e_i(t) = y_i(t) − σx_i(t), i ∈ ℐ₂, then we have the following error system:

(3.1)

Theorem 3.1. Suppose Assumption 2.3 holds; if the nonlinear controllers are chosen as follows:

(3.2)

where k_i are the feedback control gains, let

, and when

(3.3)

where ϵ₁ is a positive constant, then the GPS between the two neural networks (2.1) and (2.2) can be achieved.

Proof. Consider the Lyapunov functional candidate

(3.4)

Calculating

with respect to t along the solution of (3.1), and noticing the nonlinear feedback controllers (3.2), one has

(3.5)

By utilizing Lemma 2.4 and Assumption 2.3, we have the following four inequalities: the first one is

(3.6)

Denote

and

, and then we can get the second inequality:

(3.7)

and the third one is as follows:

(3.8)

Let

; thus, we have the last one:

(3.9)

Similarly, we can obtain the following four inequalities:

(3.10)

(3.11)

(3.12)

(3.13)

Substituting (3.6)–(3.13) into (3.5), we can obtain

(3.14)

Taking account of condition (3.3), we have .

Clearly, S = {e_i(t) = 0, k_i = k, i ∈ ℐ₂} is the largest invariant set contained in . In terms of the LaSalle invariant principle, the trajectory asymptotically converges to the largest invariant set S with any initial value of (3.1), namely, lim _t→+∞ ∥e_i(t)∥ = 0, i ∈ ℐ₂. Hence, the GPS between neural networks (2.1) and (2.2) is realized. The proof is completed.

In Theorem 3.1, the generalized projective synchronization of two different neural networks with time delay has been investigated by choosing suitable nonlinear feedback controllers. However, it requires feedback control gains to be large in u_i given by (3.2), which is not practical. Hence, it is desirable to improve the scheme for reducing the feedback control gains to be as small as possible. Now, we give the following improvement scheme.

Theorem 3.2. Suppose Assumption 2.3 holds; if the nonlinear controllers are chosen as follows:

(3.15)

where k_i are the feedback gains, denote

, and if

(3.16)

where ϵ₂ is a positive constant, then the GPS between neural networks (2.1) and (2.2) can be achieved.

Proof. Select the following Lyapunov functional candidate:

(3.17)

Differentiating V with respect to time along (3.1), we have

(3.18)

Substituting (3.6), (3.7), (3.10), and (3.11) into (3.18), we can obtain

(3.19)

By condition (3.16), we have

. Similarly, in light of the proof of Theorem 3.1, the GPS between neural networks (2.1) and (2.2) can be achieved under nonlinear controllers (3.15) too.

Remark 3.3. Comparing the infimum of the feedback control gain k in Theorem 3.2 with that in Theorem 3.1 implies that k_res = −λ_min(C₁)+α(A₁)(|σ | + θ²/|σ|)+α(B₁) | σ | + α(G ⊗ Γ₁)(|σ | + π²/|σ|)+α(G^τ ⊗ Γ₂) | σ | + α(B₁)μ²/|σ| + α(G^τ ⊗ Γ₂)π²/|σ| is the extra part compared with the needed feedback gain in Theorem 3.2. Usually, it can be considered that k_res > 0, which will be demonstrated in simulation.

Furthermore, in order to obtain much smaller feedback control gains, we choose more suitable controllers as follows.

Theorem 3.4. Suppose Assumption 2.3 holds. Under the nonlinear controllers

(3.20)

where k_i are the feedback control gains, denote

, and if

(3.21)

where ϵ₃ is some positive constant, then the GPS between the two neural networks (2.1) and (2.2) can be achieved.

Proof. Choose the same Lyapunov functional as (3.17) in the proof of Theorem 3.2, and then we can get

(3.22)

Combining (3.6), (3.7), (3.10), (3.11), and (3.22), we could change inequality (3.19) into

(3.23)

Taking into account condition (3.21), the GPS can be realized under nonlinear controllers (3.18).

Remark 3.5. It is easy to find that the infimum of k in (3.21) has one more term −λ_min(C₁) than (3.16). Because C₁ is diagonally positive definite, −λ_min(C₁) < 0 demonstrates the required k in Theorem 3.4 is smaller than the one in Theorem 3.2.

If the two neural networks (2.1) and (2.2) have identical number of nodes, node dynamics, and topological structure, that is, N₁ = N₂, C₁ = C₂, A₁ = A₂, B₁ = B₂, f₁ = f₂, g₁ = g₂, G_ij = H_ij, , and Γ₁ = Γ₂, the error system (3.1) can be rewritten as follows:

(3.24)

Thus, we can obtain the following corollary for synchronizing the error system (3.24).

Corollary 3.6. Suppose the two neural networks (2.1) and (2.2) have identical number of nodes, node dynamics, and topological structure. If the following nonlinear controllers:

(3.25)

are employed, where k_i are the feedback control gains, denote

, and when k ≥ −C₁ + α(A₁)(β² + 1) + α(B₁)(1 + γ²), the error system (3.24) can be synchronized.

Proof. We construct the Lyapunov function as follows:

(3.26)

We can conclude that k ≥ −C₁ + α(A₁)(β² + 1) + α(B₁)(1 + γ²) by using the same method as that in the above theorems.

Furthermore, let us assume that system (3.24) is without time-delay terms; then, system (3.24) reduces to

(3.27)

Then, a simpler corollary can be produced.

Corollary 3.7. The following controllers:

(3.28)

can be applied to synchronize the system (3.27) when the feedback control gain k satisfies the inequality k ≥ −C₁ + α(A₁)(β² + 1).

Similarly, in the drive network (2.1) and the response network (2.2), if , , B₁ = B₂ = 0, h₁, h₂ are linear functions and G = H = 0, the error system (3.1) can be rewritten as follows:

(3.29)

Thus, we can obtain the following corollary for synchronizing the error system (3.24).

Corollary 3.8. By applying the nonlinear controllers

(3.30)

where k_i are the feedback control gains, denote

, and when k ≥ −λ_min(C₁ + C₂) + 2α(H^τ ⊗ Γ²) + 1, the GPS between the two neural networks (2.1) and (2.2) can be achieved.

Proof. We construct the Lyapunov function as follows:

(3.31)

We can conclude that k ≥ −λ_min(C₁ + C₂) + 2α(H^τ ⊗ Γ²) + 1 by using the same method as that in the above theorems. Meanwhile, this conclusion also contains the result of [32].

It is easy to see that the theoretical feedback gains given in the above results (Theorems 3.1–3.4) are too conservative, usually much larger than the needed value; clearly, it is desirable to make the feedback gains as small as possible. Here, the adaptive technique is adopted to achieve this goal.

Theorem 3.9. Suppose that Assumption 2.3 holds and the feedback controllers are chosen as (3.20). If the feedback control gains satisfy the update law

(3.32)

(ϱ_i are arbitrary positive constants), then the GPS between the neural network (2.1) and (2.2) can be realized.

Proof. We construct the Lyapunov function as follows:

(3.33)

where ϱ is a sufficient large positive constant to be determined.

Let

(3.34)

Then we have

(3.35)

Combining (3.18) and (3.35) with (3.33), one can obtain the following inequality:

(3.36)

Therefore, according to the above proof of the three theorems, it is easy to verify the conclusion of Theorem 3.9.

4. Numerical Simulations

In this section, several examples are given to verify the conclusions established above. Consider the two neural networks (2.1) and (2.2) with the following parameters

(4.1)

and

for j = 1,2, N₁ = 6 and N₂ = 4.

Simulation 1 The four graphs in Figure 1 represent the motion trace of drive and response systems. Comparing Figures 1(b), 1(c), and 1(d) with Figure 1(a), we can find a trivial conclusion. Because the parameters in response system and the ones in drive system are very similar, the shape of the motion orbit of response systems looks like the one of drive system. But the biases between the four traces and the “0” orbit is rather different.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Trajectory of the drive system. (b) trajectory of the response system with α = 0.7. (c) trajectory of the response system with α = −0.7. (d) Trajectory of the response system with α = −1.

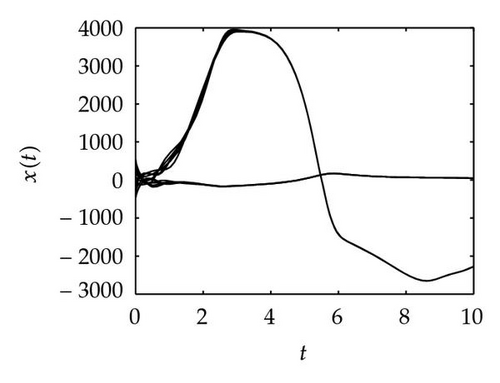
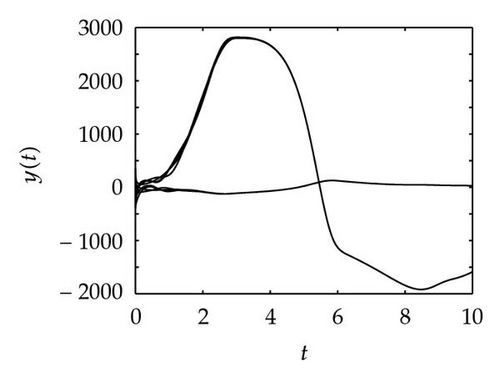
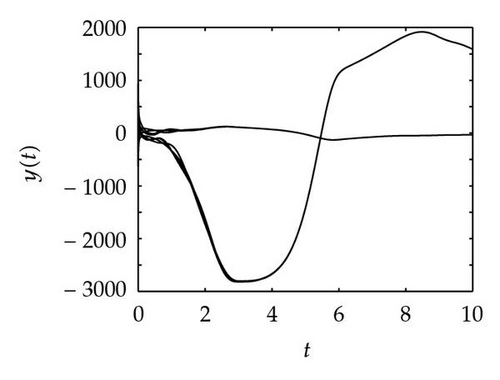
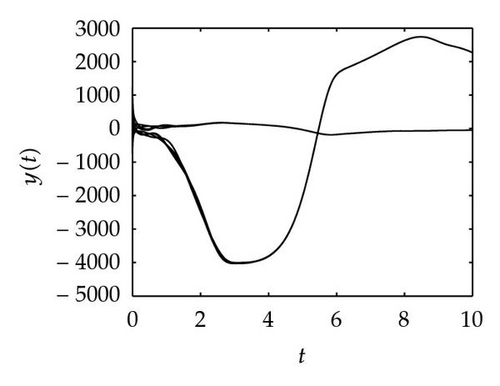
Simulation 2 Setting θ = 1, μ = 1, π = 1, β = 1, γ = 1, δ = 1, it is easy to verify that Assumption 2.3 holds. Choose x_ij(t) = 100(12 − 3i − j) and x_ij(t) = 100(−8 + 3i + j) for t ≤ 0 as the initial values and define

(4.2)

for measuring the process of projective synchronization.

In Figure 2, the top three plots present the synchronization process of drive system with α = 0.7, −0.7, −1, respectively; the middle three graphs demonstrate the change trend of E_y as t → ∞ with the former three projective factors; the bottom three ones represent the synchronization trace of the two neural networks for the three αs. The nine figures say that, for different α, the required synchronization times are all in the interval [4, 6]. However, the change amplitudes of the nine curves show obvious differences. By the same way, for the three projective factors, we can provide the three infimums of feedback control gains that are k ≥ 40.65 with α = 0.7, k ≥ 40.65 with α = −0.7 and k ≥ 39.33 with α = −1, respectively.

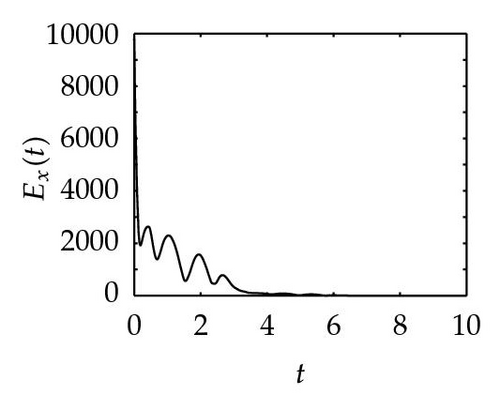
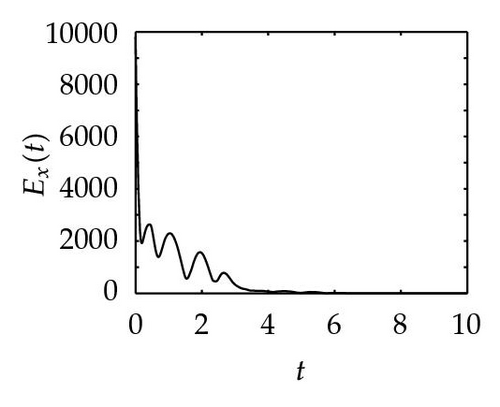
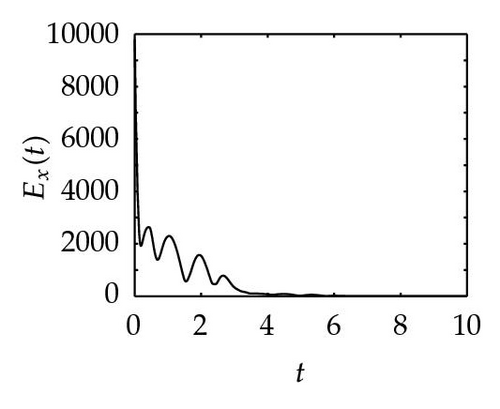
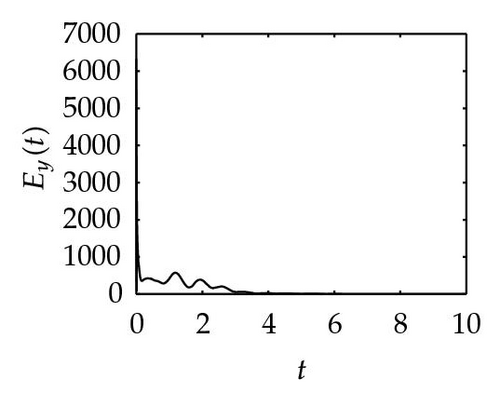
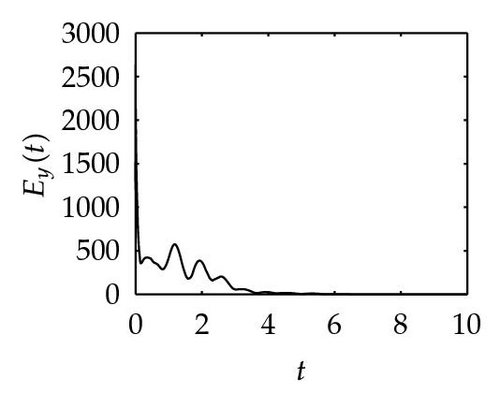
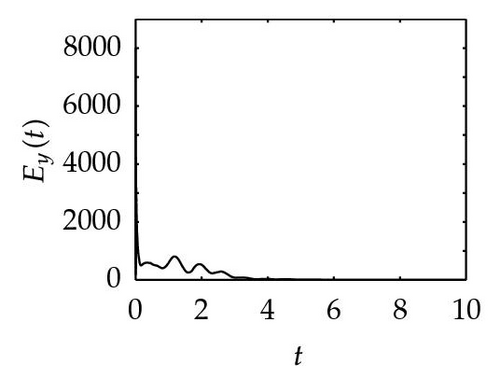
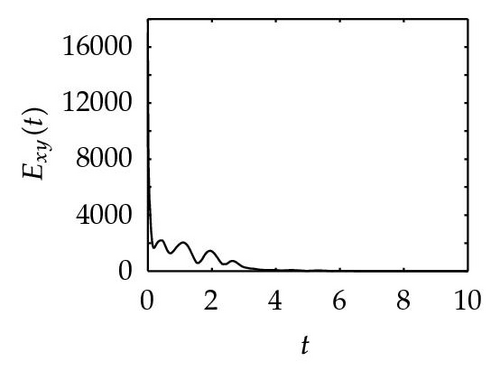
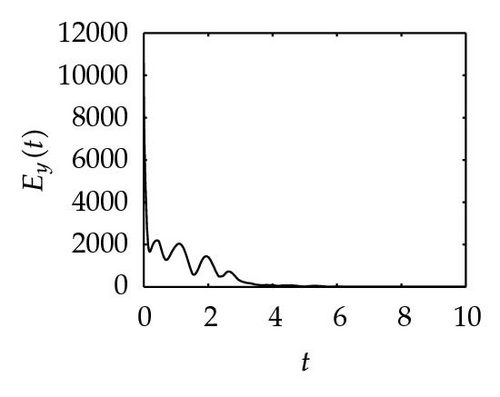
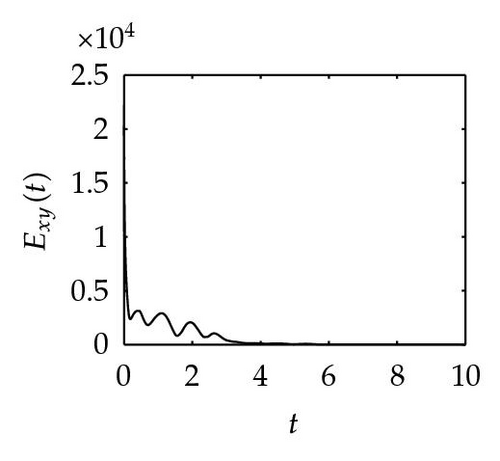
Remark 4.1. The reason why we apply three different nonlinear controllers for obtaining Theorems 1, 2, and 3 is that we want to find smaller feedback control gain. By computing, we have k ≥ 40.65 for Theorem 3.1, k ≥ 21.43 for Theorem 3.2, and k ≥ 20.43 for Theorem 3.4, respectively. It shows that our conjecture and simulation meet these results.

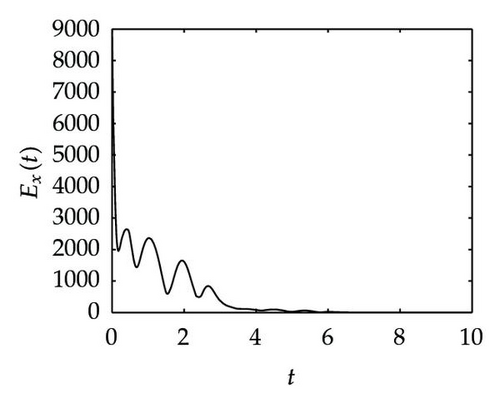
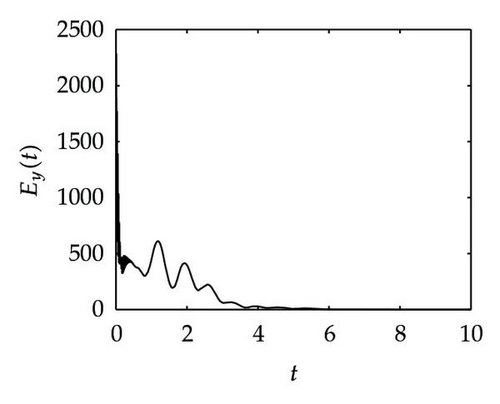
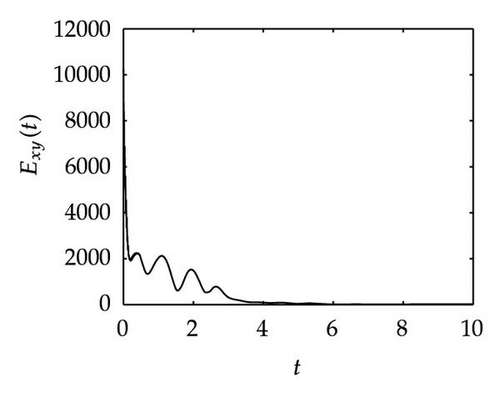
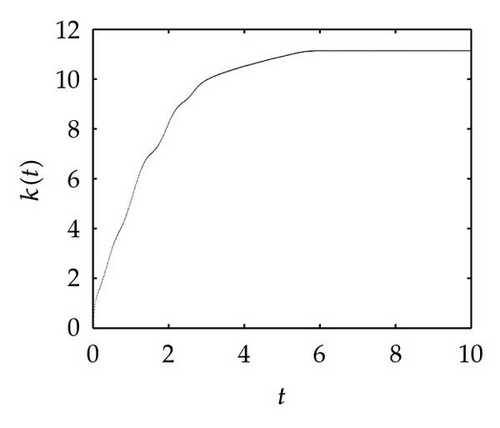
Simulation 3 In this simulation, we want to verify the synchronization process of the two neural networks when an adaptive control is applied to the response system. Figure 3 shows the time evolution of E_x, E_y, E_xy and k(t), as well as the fourth plot Figure 3(d) tell us that the feedback control gain trends towards 11.15 approximately as t → ∞ which is far lower than 39.33. Actually, this proves that the adaptive control method can diminish the feedback control gain.

5. Conclusion

The GPS between two neural networks with mixed time delays and different parameters was investigated in this paper. By means of the Lyapunov stability theories, the GPS was realized under control of three nonlinear controllers. By comparison, we found that the nonlinear controller in Theorem 3.4 was simpler and easier to ensure that the GPS was achieved. Therefore, it was also applied in practical design. According to the optimal nonlinear controller, an adaptive update technique was designed to guarantee that the feedback control gain was sufficiently small. Eventually, several numerical simulations verified the validity of those results.

Acknowledgments

The authors thank the referees and the editor for their valuable comments on this paper. This work was supported by the National Science Foundation of China under Grant no. 61070087, the Guangdong Education University Industry Cooperation Projects (2009B090300355), the Foundation for Distinguished Young Talents in Higher Education of Guangdong (LYM11115), the Shenzhen Basic Research Project (JC200903120040A, JC201006010743A), and the Shenzhen Polytechnic Youth Innovation Project (2210k3010020).

References

1 Strogatz S. H., Exploring complex networks, Nature. (2001) 410, no. 6825, 268–276, 2-s2.0-0035826155, https://doi.org/10.1038/35065725.
10.1038/35065725
CAS PubMed Web of Science® Google Scholar
2 Newman M. E. J., The structure and function of complex networks, SIAM Review. (2003) 45, no. 2, 167–256, https://doi.org/10.1137/S003614450342480, 2010377.
10.1137/S003614450342480
Web of Science® Google Scholar
3 Barabási A.-L., Scale-free networks: a decade and beyond, American Association for the Advancement of Science. (2009) 325, no. 5939, 412–413, https://doi.org/10.1126/science.1173299, 2548299.
10.1126/science.1173299
CAS Google Scholar
4 Butts C. T., Revisiting the foundations of network analysis, American Association for the Advancement of Science. (2009) 325, no. 5939, 414–416, https://doi.org/10.1126/science.1171022, 2548300.
10.1126/science.1171022
CAS Web of Science® Google Scholar
5 Centola D., The spread of behavior in an online social network experiment, Science. (2010) 329, no. 5996, 1194–1197, 2-s2.0-77956296152, https://doi.org/10.1126/science.1185231.
10.1126/science.1185231
CAS PubMed Web of Science® Google Scholar
6 Shinar G. and Feinberg M., Structural sources of robustness in biochemical reaction networks, Science. (2010) 327, no. 5971, 1389–1391, 2-s2.0-77949398351, https://doi.org/10.1126/science.1183372.
10.1126/science.1183372
CAS PubMed Web of Science® Google Scholar
7 Yu W., Cao J., and Lü J., Global synchronization of linearly hybrid coupled networks with time-varying delay, SIAM Journal on Applied Dynamical Systems. (2008) 7, no. 1, 108–133, https://doi.org/10.1137/070679090, 2399559.
10.1137/070679090
Web of Science® Google Scholar
8 Wang K., Fu X., and Li K., Cluster synchronization in community networks with nonidentical nodes, Chaos. (2009) 19, no. 2, 10, 023106, https://doi.org/10.1063/1.3125714, 2548747.
10.1063/1.3125714
PubMed Web of Science® Google Scholar
9 Lü J. and Chen G., A time-varying complex dynamical network model and its controlled synchronization criteria, Institute of Electrical and Electronics Engineers. (2005) 50, no. 6, 841–846, https://doi.org/10.1109/TAC.2005.849233, 2142000.
10.1109/TAC.2005.849233
Google Scholar
10 Wang J.-W., Ma Q., Zeng L., and Abd-Elouahab M. S., Mixed outer synchronization of coupled complex networks with time-varying coupling delay, Chaos. (2011) 21, no. 1, 8, 013121, https://doi.org/10.1063/1.3555836, 2808176.
10.1063/1.3555836
PubMed Web of Science® Google Scholar
11 Zhu Q. and Cao J., Adaptive synchronization under almost every initial data for stochastic neural networks with time-varying delays and distributed delays, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 4, 2139–2159, https://doi.org/10.1016/j.cnsns.2010.08.037, 2736078.
10.1016/j.cnsns.2010.08.037
Web of Science® Google Scholar
12 Gan Q., Xu R., and Kang X., Synchronization of chaotic neural networks with mixed time delays, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 2, 966–974, https://doi.org/10.1016/j.cnsns.2010.04.036, 2725818.
10.1016/j.cnsns.2010.04.036
Web of Science® Google Scholar
13 Kanter I., Zigzag M., Englert A., Geissler F., and Kinzel W., Synchronization of unidirectional time delay chaotic networks and the greatest common divisor, EPL. (2011) 93, no. 6, 2-s2.0-79953652988, https://doi.org/10.1209/0295-5075/93/60003, 60003.
10.1209/0295-5075/93/60003
Web of Science® Google Scholar
14 Sudheer K. S. and Sabir M., Adaptive modified function projective synchronization of multiple time-delayed chaotic Rossler system, Physics Letters, Section A. (2011) 375, no. 8, 1176–1178, 2-s2.0-79651471414, https://doi.org/10.1016/j.physleta.2011.01.028.
10.1016/j.physleta.2011.01.028
CAS Web of Science® Google Scholar
15 Zhang C. K., He Y., and Wu M., Exponential synchronization of neural networks with time-varying mixed delays and sampled-data, Neurocomputing. (2010) 74, no. 1–3, 265–273, 2-s2.0-78649452605, https://doi.org/10.1016/j.neucom.2010.03.020.
10.1016/j.neucom.2010.03.020
Web of Science® Google Scholar
16 Ahn C. K., Anti-synchronization of time-delayed chaotic neural networks based on adaptive control, International Journal of Theoretical Physics. (2009) 48, no. 12, 3498–3509, 2-s2.0-71049162464, https://doi.org/10.1007/s10773-009-0154-3.
10.1007/s10773-009-0154-3
Web of Science® Google Scholar
17 Ahn C. K., Adaptive H∞ anti-synchronization for time-delayed chaotic neural networks, Progress of Theoretical Physics. (2009) 122, no. 6, 1391–1403, 2-s2.0-77949413433, https://doi.org/10.1143/PTP.122.1391.
10.1143/PTP.122.1391
Google Scholar
18 Ge Z. M., Wong Y. T., and Li S. Y., Temporary lag and anticipated synchronization and anti-synchronization of uncoupled time-delayed chaotic systems, Journal of Sound and Vibration. (2008) 318, no. 1-2, 267–278, 2-s2.0-49049103524, https://doi.org/10.1016/j.jsv.2008.03.062.
10.1016/j.jsv.2008.03.062
Web of Science® Google Scholar
19 Prasad A., Kurths J., and Ramaswamy R., The effect of time-delay on anomalous phase synchronization, Physics Letters, Section A. (2008) 372, no. 40, 6150–6154, 2-s2.0-51349096800, https://doi.org/10.1016/j.physleta.2008.08.043.
10.1016/j.physleta.2008.08.043
CAS Web of Science® Google Scholar
20 Ghosh D., Ray A., and Chowdhury A. R., Generalized and phase synchronization between two different time-delayed systems, Modern Physics Letters B. (2008) 22, no. 19, 1867–1878, 2-s2.0-51149093472, https://doi.org/10.1142/S0217984908016546.
10.1142/S0217984908016546
CAS Web of Science® Google Scholar
21 Senthilkumar D. V., Lakshmanan M., and Kurths J., Transition from phase to generalized synchronization in time-delay systems, Chaos. (2008) 18, no. 2, 12, 2-s2.0-46449096998, https://doi.org/10.1063/1.2911541, 023118.
10.1063/1.2911541
CAS PubMed Web of Science® Google Scholar
22 Zhang D. and Xu J., Projective synchronization of different chaotic time-delayed neural networks based on integral sliding mode controller, Applied Mathematics and Computation. (2010) 217, no. 1, 164–174, https://doi.org/10.1016/j.amc.2010.05.037, 2672574.
10.1016/j.amc.2010.05.037
Web of Science® Google Scholar
23 Ghosh D., Generalized projective synchronization in time-delayed systems: nonlinear observer approach, Chaos. (2009) 19, no. 1, 9, 013102, https://doi.org/10.1063/1.3054711, 2513753.
10.1063/1.3054711
PubMed Web of Science® Google Scholar
24 Ghosh D., Banerjee S., and Roy Chowdhury A., Generalized and projective synchronization in modulated time-delayed systems, Physics Letters, Section A. (2010) 374, no. 21, 2143–2149, 2-s2.0-77950516775, https://doi.org/10.1016/j.physleta.2010.03.027.
10.1016/j.physleta.2010.03.027
CAS Web of Science® Google Scholar
25 Vasegh N. and Khellat F., Projective synchronization of chaotic time-delayed systems via sliding mode controller, Chaos, Solitons and Fractals. (2009) 42, no. 2, 1054–1061, 2-s2.0-67650077093, https://doi.org/10.1016/j.chaos.2009.02.037.
10.1016/j.chaos.2009.02.037
Web of Science® Google Scholar
26 Ghosh D., Saha P., and Roy Chowdhury A., Linear observer based projective synchronization in delay Rössler system, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 6, 1640–1647, https://doi.org/10.1016/j.cnsns.2009.06.019, 2576790.
10.1016/j.cnsns.2009.06.019
Web of Science® Google Scholar
27 Gan Q., Xu R., and Kang X., Synchronization of chaotic neural networks with mixed time delays, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 2, 966–974, https://doi.org/10.1016/j.cnsns.2010.04.036, 2725818.
10.1016/j.cnsns.2010.04.036
Web of Science® Google Scholar
28 Chen J., Jiao L., Wu J., and Wang X., Projective synchronization with different scale factors in a drivenresponse complex network and its application in image encryption, Nonlinear Analysis. (2010) 11, no. 4, 3045–3058, 2-s2.0-77955775398, https://doi.org/10.1016/j.nonrwa.2009.11.003.
10.1016/j.nonrwa.2009.11.003
Google Scholar
29 Feng C. F., Xu X. J., Wang S. J., and Wang Y. H., Projective-anticipating, projective, and projective-lag synchronization of time-delayed chaotic systems on random networks, Chaos. (2008) 18, no. 2, 6, 2-s2.0-46449133654, https://doi.org/10.1063/1.2912720, 023117.
10.1063/1.2912720
PubMed Web of Science® Google Scholar
30 Wang J.-W., Ma Q., Zeng L., and Abd-Elouahab M. S., Mixed outer synchronization of coupled complex networks with time-varying coupling delay, Chaos. (2011) 21, no. 1, 8, 013121, https://doi.org/10.1063/1.3555836, 2808176.
10.1063/1.3555836
PubMed Web of Science® Google Scholar
31 Zheng S., Bi Q., and Cai G., Adaptive projective synchronization in complex networks with time-varying coupling delay, Physics Letters. A. (2009) 373, no. 17, 1553–1559, https://doi.org/10.1016/j.physleta.2009.03.001, 2513416.
10.1016/j.physleta.2009.03.001
CAS Web of Science® Google Scholar
32 Wu X. and Lu H., Generalized projective synchronization between two different general complex dynamical networks with delayed coupling, Physics Letters, Section A. (2010) 374, no. 38, 3932–3941, 2-s2.0-77955920162, https://doi.org/10.1016/j.physleta.2010.07.059.
10.1016/j.physleta.2010.07.059
CAS Web of Science® Google Scholar
33 Wu W., Zhou W., and Chen T., Cluster synchronization of linearly coupled complex networks under pinning control, IEEE Transactions on Circuits and Systems. I. (2009) 56, no. 4, 829–839, https://doi.org/10.1109/TCSI.2008.2003373, 2724977.
10.1109/TCSI.2008.2003373
Web of Science® Google Scholar

Citing Literature

All articles

Generalized Projective Synchronization between Two Different Neural Networks with Mixed Time Delays

Abstract

1. Introduction

2. Model Description and Preliminaries

3. GPS between Two Different Neural Networks with Mixed Time Delays

4. Numerical Simulations

5. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Generalized Projective Synchronization between Two Different Neural Networks with Mixed Time Delays

Abstract

1. Introduction

2. Model Description and Preliminaries

3. GPS between Two Different Neural Networks with Mixed Time Delays

4. Numerical Simulations

5. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information