Recently, Xiao et al. proposed a nonsmooth equations-based method to solve the ℓ₁-norm minimization problem (2011). The advantage of this method is its simplicity and lower storage. In this paper, based on new nonsmooth equations reformulation, we investigate new nonsmooth equations-based algorithms for solving ℓ₁-norm minimization problems. Under mild conditions, we show that the proposed algorithms are globally convergent. The preliminary numerical results demonstrate the effectiveness of the proposed algorithms.

1. Introduction

We consider the ℓ₁-norm minimization problem

()

where x ∈ ℝⁿ, b ∈ ℝ^m, A ∈ ℝ^m×n, and ρ is a nonnegative parameter. Throughout the paper, we use

and ∥v∥₁ = ∑_i | v_i| to denote the Euclidean norm and the ℓ₁-norm of vector v ∈ Rⁿ, respectively. Problem (1.1) has many important practical applications, particularly in compressed sensing (abbreviated as CS) [1] and image restoration [2]. It can also be viewed as a regularization technique to overcome the ill-conditioned, or even singular, nature of matrix A, when trying to infer x from noiseless observations b = Ax or from noisy observations b = Ax + ξ, where ξ is the white Gaussian noise of variance σ² [3–5].

The convex optimization problem (1.1) can be cast as a second-order cone programming problem and thus could be solved via interior point methods. However, in many applications, the problem is not only large scale but also involves dense matrix data, which often precludes the use and potential advantage of sophisticated interior point methods. This motivated the search of simpler first-order algorithms for solving (1.1), where the dominant computational effort is a relatively cheap matrix-vector multiplication involving A and A^T. In the past few years, several first-order algorithms have been proposed. One of the most popular algorithms falls into the iterative shrinkage/thresholding (IST) class [6, 7]. It was first designed for wavelet-based image deconvolution problems [8] and analyzed subsequently by many authors, see, for example, [9–11]. Figueiredo et al. [12] studied the gradient projection and Barzilai-Borwein method [13] (denoted by GPSR-BB) for solving (1.1). They reformulated problem (1.1) as a box-constrained quadratic program and solved it by a gradient projection and Barzilai-Borwein method. Wright et al. [14] presented sparse reconstruction algorithm (denoted by SPARSA) to solve (1.1). Yun and Toh [15] proposed a block coordinate gradient descent algorithm for solving (1.1). Yang and Zhang [16] investigated alternating direction algorithms for solving (1.1).

Quite recently, Xiao et al. [17] developed a nonsmooth equations-based algorithm (called SGCS) for solving ℓ₁-norm minimization problems in CS. They reformulated the box-constrained quadratic program obtained by Figueiredo et al. [12] into a system of nonsmooth equations and then applied the spectral gradient projection method [18] to solving the nonsmooth equation. The main advantage of the SGCS is its simplicity and lower storage. The difference between the above algorithms and SGCS is that SGCS did not use line search to decrease the value of objective function at each iteration and instead used a projection step to accelerate the iterative process. However, each projection step in SGCS requires two matrix-vector multiplication involving A or A^T, which means that each iteration requires matrix-vector multiplication involving A or A^T four times, while each iteration in GPSR-BB and IST is only two times. This may bring in more computational complexity. In addition, the dimension of the system of nonsmooth equations is 2n, which is twice of the original problems. These drawbacks motivate us to study new nonsmooth equations-based algorithms for the ℓ₁-norm minimization problem.

In this paper, we first reformulate problem (1.1) into a system of nonsmooth equations. This system is Lipschitz continuous and monotone and many effective algorithms (see, e.g., [18–22]) can be used to solve it. We then apply spectral gradient projection (denoted by SGP) method [18] to solve the resulting system. Similar to SGCS, each iteration in SGP requires matrix-vector multiplication involving A or A^T four times. In order to reduce the computational complexity, we also propose a modified SGP (denoted by MSGP) method to solve the resulting system. Under mild conditions, the global convergence of the proposed algorithms will be ensured.

The remainder of the paper is organized as follows. In Section 2, we first review some existing results of nonsmooth analysis and then derive an equivalent system of nonsmooth equations to problem (1.1). We verify some nice properties of the resulting system in this section. In Section 3, we propose the algorithms and establish their global convergence. In Section 4, we apply the proposed algorithms to some practical problems arising from compressed sensing and image restoration and compare their performance with that of SGCS, SPARSA, and GPSR-BB.

Throughout the paper, we use 〈· , ·〉 to denote the inner product of two vectors in Rⁿ.

2. Preliminaries

By nonsmooth analysis, a necessary condition for a vector x ∈ ℝⁿ to be a local minima of nonsmooth function f : ℝⁿ → ℝ is that

()

where ∂f(x) denotes the subdifferential of f at x [23]. If f is convex, then (2.1) is also sufficient for x to be a solution of (1.1). The subdifferential of the absolute value function |t| is given by the signum function sign(t), that is

()

For problem (1.1), the optimality conditions therefore translate to

()

where ∇_if(x) = ∂f(x)/∂x_i, i = 1, …, n. It is clear that the function defined by (1.1) is convex. Therefore a point x^* ∈ Rⁿ is a solution of problem (1.1) if and only if it satisfies

()

Formally, we call the above conditions the optimality conditions for problem (1.1).

For any given τ > 0, we define a mapping

()

Then H^τ is a continuous mapping and is closely related to problem (1.1). It is generally not differentiable in the sense of Fréchet derivative but semismooth in the sense of Qi and Sun [24]. The following proposition shows that the ℓ₁-norm minimization problem (1.1) is equivalent to a nonsmooth equation. It can be easily obtained by the use of the optimality conditions and the convexity of the function f defined by (1.1).

Proposition 2.1. Let τ > 0 be any given constant. A point x^* ∈ ℝⁿ is a solution of problem (1.1) if and only if it satisfies

()

The above proposition has reformulated problem (1.1) as a system of nonsmooth equations. Compared with the nonsmooth equation reformulation in [17], the dimension of (2.6) is only half of the dimension of the equation in [17].

Given a, b, c, d ∈ ℝ. It is easy to verify that (see, e.g. [25])

()

with

()

It is clear that 0 ≤ s, t ≤ 1. By (2.5), we have for any x, y ∈ ℝⁿ, it holds that

()

where 0 ≤ s_i, t_i ≤ 1. Define two diagonal matrixes S and T by

()

Then we obtain

()

Since ∇f(x) = A^T(Ax − b), we get

()

The next proposition shows the Lipschitz continuity of H^τ defined by (2.5).

Proposition 2.2. For each τ > 0, there exists a positive constant L(τ) such that

()

Proof. By (2.10) and (2.12), we have

()

Let L(τ)≜1 + τ∥A^TA∥. Then (2.13) holds. The proof is complete.

The following proposition shows another good property of the system of nonsmooth equations (2.6).

Proposition 2.3. There exists a constant τ^* > 0 such that for any 0 < τ ≤ τ^*, the mapping H^τ : ℝⁿ → ℝⁿ is monotone, that is

()

Proof. Let D_ii be the ith diagonal element of A^TA. It is clear that D_ii > 0, i = 1, …, n. Set τ^*≜min_i{1/D_ii}. Note that A^TA is symmetric and positive semidefinite. Consequently, for any τ ∈ (0, τ^*], matrix T(I − S) + τ(I − T + TS)A^TA is also positive semidefinite. Therefore, it follows from (2.12) that

()

This completes the proof.

3. Algorithms and Their Convergence

In this section, we describe the proposed algorithms in detail and establish their convergence. Let τ > 0 be given. For simplicity, we omit τ and abbreviate H^τ(·) as H(·).

Algorithm 3.1 . (spectral gradient projection method (abbreviated as SGP)). Given initial point x₀ ∈ ℝⁿ and constants θ₀ = 1, r > 0, ν ≥ 0, σ > 0, γ ∈ (0,1). Set k : = 0.

Step 1. Compute d_k by

()

where for each k ≥ 1, θ_k is defined by

()

with s_k−1 = x_k − x_k−1 and

. Stop if d_k = 0.

Step 2. Determine steplength with m_k being the smallest nonnegative integer m such that

()

Set z_k : = x_k + α_kd_k. Stop if ∥H(z_k)∥ = 0.

Step 3. Compute

()

Set k : = k + 1, and go to Step 1.

Remark 3.2. (i) The idea of the above algorithm comes from [18]. The major difference between Algorithm 3.1 and the method in [18] lies in the definition of y_k−1. The choice of y_k−1 in Step 1 follows from the modified BFGS method [26]. The purpose of the term is to make y_k−1 be closer to H(x_k) − H(x_k−1) as x_k tends to a solution of (2.6).

(ii) Step 3 is called the projection step. It is originated in [20]. The advantage of the projection step is to make x_k+1 closer to the solution set of (2.6) than x_k. We refer to [20] for details.

(iii) Since −〈H(x_k), d_k〉 = ∥H(x_k)∥∥d_k∥, by the continuity of H, it is easy to see that inequality (3.3) holds for all m sufficiently large. Therefore Step 2 is well defined and so is Algorithm 3.1.

The following lemma comes from [20].

Lemma 3.3. Let H : ℝⁿ → ℝⁿ be monotone and x, y ∈ ℝⁿ satisfy 〈H(y), x − y〉>0. Let

()

Then for any x^* ∈ ℝⁿ satisfying H(x^*) = 0, it holds that

()

The following theorem establishes the global convergence for Algorithm 3.1.

Theorem 3.4. Let {x_k} be generated by Algorithm 3.1 and x^* a solution of (2.6). Then one has

()

In particular, {x_k} is bounded. Furthermore, it holds that either {x_k} is finite and the last iterate is a solution of the system of nonsmooth equations (2.6), or the sequence is infinite and lim_k→∞∥x_k+1 − x_k∥ = 0. Moreover, {x_k} converges to some solution of (2.6).

Proof. The proof is similar to that in [18]. We omit it here.

Remark 3.5. The computational complexity of each of SGP’s steps is clear. In large-scale problems, most of the work is matrix-vector multiplication involving A and A^T. Steps 1 and 2 of SGP require matrix-vector multiplication involving A or A^T two times each, while each iteration in GPSR-BB involves matrix-vector multiplication only two times. This may bring in more computational complexity. Therefore, we give a modification of SGP. The modified algorithm, which will be called MSGP in the rest of the paper, coincides with SGP except at Step 3, whose description is given below.

Algorithm 3.6 (modified spectral gradient projection Method (abbreviated as MSGP)). Given initial point x₀ ∈ ℝⁿ and constants θ₀ = 1, r > 0, σ > 0, γ ∈ (0,1) a positive integer M. Set k : = 0.

Step 3. Let m = k/M. If m is a positive integer, compute

()

otherwise, let x_k+1 = z_k. Set k : = k + 1, and go to Step 1.

Lemma 3.7. Assume that {x_k} is a sequence generated by Algorithm 3.6 and x^* ∈ ℝⁿ satisfies H(x^*) = 0. Let λ_max(A^TA) be the maximum eigenvalue of A^TA and τ ∈ (0,1/λ_max(A^TA)]. Then it holds that

()

Proof. Let x_k+1 be generated by (3.8). It follows from Lemma 3.3 that (3.9) holds. In the following, we assume that x_k+1 = z_k. Then, we obtain

()

This together with (2.12) implies that

()

Let τ ∈ (0,1/λ_max(A^TA)]. Then we get

()

This completes the proof.

Now we establish a global convergence theorem for Algorithm 3.6.

Theorem 3.8. Let λ_max(A^TA) be the maximum eigenvalue of A^TA and τ ∈ (0,1/λ_max(A^TA)]. Assume that {x_k} is generated by Algorithm 3.6 and x^* is a solution of (2.6). Then one has

()

Proof. We first note that if the algorithm terminates at some iteration k, then we have d_k = 0 or ∥H(z_k)∥ = 0. By the definition of θ_k, we have H(x_k) = 0 if d_k = 0. This shows that either x_k or z_k is a solution of (2.6).

Suppose that d_k ≠ 0 and ∥H(z_k)∥ ≠ 0 for all k. Then an infinite sequence {x_k} is generated. It follows from (3.3) that

()

Let x^* be an arbitrary solution of (2.6). By Lemmas 3.7 and 3.3, we obtain

()

where m is a nonnegative integer. In particular, the sequence {∥x_k − x^*∥} is nonincreasing and hence convergent. Moreover, the sequence {x_k} is bounded, and

()

Following from (3.8) and (3.14), we have

()

This together with (3.16) yields

()

Now we consider the following two possible cases:

(i)
liminf_m→∞∥H(x_mM)∥ = 0;
(ii)
liminf_m→∞∥H(x_mM)∥ = ϵ > 0.

If (i) holds, then by the continuity of H and the boundedness of {x_mM}, it is clear that the sequence {x_mM} has some accumulation point x^* such that H(x^*) = 0. Since the sequence {∥x_k − x^*∥} converges, it must hold that {x_k} converges to x^*.

If (ii) holds, then by the boundedness of {x_mM} and the continuity of H, there exist a positive constant C and a positive integer m₀ such that

()

On the other hand, from (3.2) and the definitions of s_k−1 and y_k−1, we have

()

which together with (3.19) and Propositions 2.2 and 2.3 implies

()

Consequently, we obtain from (3.1), (3.19), and (3.21)

()

Therefore, it follows from (3.18) that lim_m→∞α_mM = 0. By the line search rule, we have for all m sufficiently large, m_k − 1 will not satisfy (3.3). This means

()

Since {x_mM} and {d_mM} are bounded, we can choose subsequences of {x_mM} and {d_mM} converging to x^** and d^**, respectively. Taking the limit in (3.23) for the subsequence, we obtain

()

However, it is not difficult to deduce from (3.1), (3.19), and (3.21) that

()

This yields a contradiction. Consequently, lim inf_m→∞∥H(x_mM)∥ = ϵ > 0 is not possible. The proof is then complete.

4. Applications to Compressed Sensing and Image Restoration

In this section, we apply the proposed algorithms, that is, SGP and MSGP, to solve some practical problems arising from the compressed sensing and image restoration. We will compare the proposed algorithms with SGCS, SPARSA, and GPSR-BB. The system of nonsmooth equations in SGCS is

()

where z, c, H are defined as those in [17]. The test problems are associated with applications in the areas of compressed sensing and image restoration. All experiments were carried out on a Lenovo PC (2.53 GHz, 2.00 GB of RAM) using Matlab 7.8. The parameters in SGCS are specified as follows:

()

The parameters in SGP and MSGP are specified as follows:

()

Throughout the experiments, we choose the initial iterate to be x⁰ = 0.

In our first experiment, we consider a typical CS scenario, where the goal is to reconstruct a length-n sparse signal (in the canonical basis) from m observations, where m < n. The m × n matrix A is obtained by first filling it with independent samples of the standard Gaussian distribution and then orthonormalizing the rows. Due to the storage limitations of PC, we test a small size signal with m = 1024, n = 4096. The observed vector is b = Ax_orig + ξ, where ξ is Gaussian white noise with variance σ² = 10⁻⁴ and x_orig is the original signal with 50 randomly placed ±1 spikes and with zeros in the remaining elements. The regularization parameter is chosen as

. We compare the performance of SGP and MSGP with that of SGCS, SPARSA, and GPSR-BB by solving the problem and choose ν = 1 in SGP and MSGP algorithms. We measure the quality of restoration by means of mean squared error (MSE) to the original signal x_orig defined by

()

where x is the restored signal. To perform this comparison, we first run the SGCS algorithm and stop the algorithm if the following inequality is satisfied:

()

and then run each of the other algorithms until each reaches the same value of the objective function reached by SGCS.

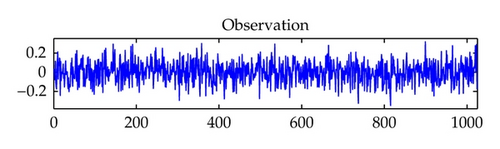
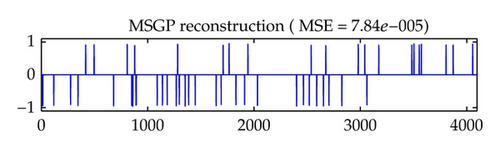
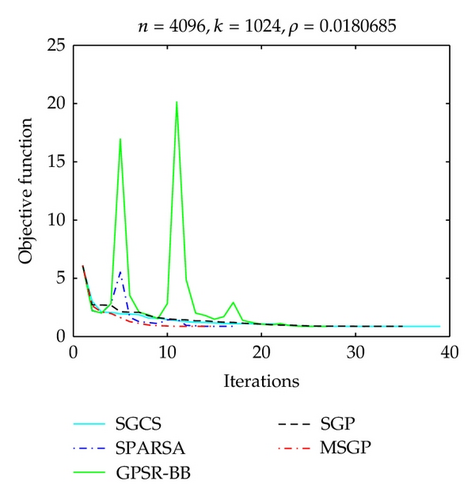
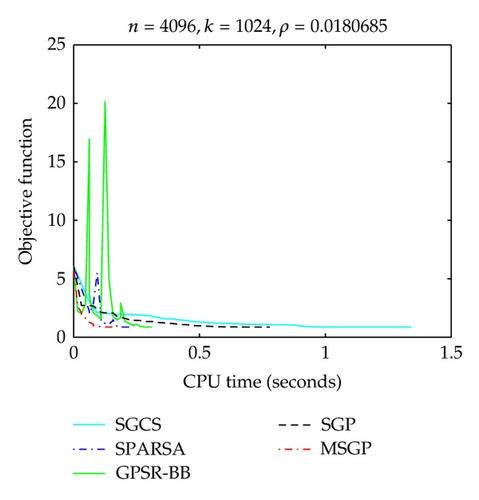
The original signal and the estimation obtained by solving (1.1) using the MSGP method are shown in Figure 1. We can see from Figure 1 that MSGP does an excellent job at locating the spikes with respect to the original signal. In Figure 2, we plot the evolution of the objective function versus iteration number and CPU time, for these algorithms. It is readily to see that MSGP worked faster than other algorithms.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

From top to bottom: original signal, observation, and reconstruction obtained by MSGP.

In the second experiment, we test MSGP for three image restoration problems based on the images as House, Cameraman, and Barbara. House and Cameraman images are of size 256 × 256 and the other is of size 512 × 512. All the pixels are contaminated by Gaussian noise with the standard deviation of 0.05 with blurring. The blurring function is chosen to be a two-dimensional Gaussian,

()

truncated such that the function has a support of 9 × 9. The image restoration problem has the form (1.1), where ρ = 0.0005 and A = HW are the composition of the 9 × 9 uniform blur matrix and the Haar discrete wavelet transform (DWT) operator. We compare the performance of MSGP with that of SGCS, SPARSA, and GPSR-BB by solving the problem and choose ν = 0 in the MSGP method. As usual, we measure the quality of restoration by signal-to-noise ratio (SNR) defined as

()

where x_orig and x are the original and restored images, respectively. We first run SGCS and stop the process if the following inequality is satisfied:

()

and then run the other algorithms until their objective function value reach SGCS′s value. Table 1 reports the number of iterations (Iter), the CPU time in seconds (Time), and the SNR to the original images (SNR).

Table 1. Test results for SGCS, SPARSA, GPSR-BB, SGP, and MSGP in image restoration.

Ima	SGCS			SPARSA			GPSR-BB			SGP			MSGP
Ima	Iter	Time	SNR	Iter	Time	SNR	Iter	Time	SNR	Iter	Time	SNR	Iter	Time	SNR
House	53	12.15	30.68	19	0.85	30.35	25	1.28	30.44	38	5.27	30.61	16	0.78	30.82
Cameraman	59	9.55	22.42	19	0.87	23.64	23	1.06	22.67	48	4.81	22.50	17	0.79	23.36
Barbara	150	234.05	22.95	29	7.08	23.72	41	12.78	22.93	62	42.12	23.06	26	6.92	23.09

It is easy to see from Table 1 that the MSGP is competitive with the well-known algorithms: SPARSA and GPSR-BB, in computing time and number of iterations and improves the SGCS greatly. Therefore we conclude that the MSGP provides a valid approach for solving ℓ₁-norm minimization problems arising from image restoration problems.

Preliminary numerical experiments show that SGP and MSGP algorithms have improved SGCS algorithm greatly. This may be because the system of nonsmooth equations solved here has lower dimension than that in [17] and the modification to projection steps that we made reduces the computational complexity.

Acknowledgments

The authors would like to thank the anonymous referee for the valuable suggestions and comments. L. Wu was supported by the NNSF of China under Grant 11071087; Z. Sun was supported by the NNSF of China under Grants 11126147 and 11201197.

References

1 Donoho D. L., Compressed sensing, IEEE Transactions on Information Theory. (2006) 52, no. 4, 1289–1306, https://doi.org/10.1109/TIT.2006.871582, 2241189, ZBL1163.94399.
10.1109/TIT.2006.871582
Web of Science® Google Scholar
2 Elad M., Matalon B., and Zibulevsky M., Image denoising with shrinkage and redundant representations, Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR ′06), June 2006, New York, NY, USA, 1924–1931, 2-s2.0-33845588006, https://doi.org/10.1109/CVPR.2006.143.
10.1109/CVPR.2006.143
Google Scholar
3 Alliney S. and Ruzinsky S. A., An algorithm for the minimization of mixed ℓ₁ and ℓ₂ norms with application to Bayesian estimation, IEEE Transactions on Signal Processing. (1994) 42, no. 3, 618–627, 2-s2.0-0028386025, https://doi.org/10.1109/78.277854.
10.1109/78.277854
Web of Science® Google Scholar
4 Candès E. J., Romberg J. K., and Tao T., Stable signal recovery from incomplete and inaccurate measurements, Communications on Pure and Applied Mathematics. (2006) 59, no. 8, 1207–1223, https://doi.org/10.1002/cpa.20124, 2230846, ZBL1098.94009.
10.1002/cpa.20124
Web of Science® Google Scholar
5 Donoho D. L., For most large underdetermined systems of linear equations the minimal ℓ₁-norm solution is also the sparsest solution, Communications on Pure and Applied Mathematics. (2006) 59, no. 6, 797–829, https://doi.org/10.1002/cpa.20132, 2217606.
10.1002/cpa.20132
Web of Science® Google Scholar
6 Daubechies I., Defrise M., and De Mol C., An iterative thresholding algorithm for linear inverse problems with a sparsity constraint, Communications on Pure and Applied Mathematics. (2004) 57, no. 11, 1413–1457, https://doi.org/10.1002/cpa.20042, 2077704, ZBL1077.65055.
10.1002/cpa.20042
Web of Science® Google Scholar
7 De Mol C. and Defrise M., A note on wavelet-based inversion algorithms, Contemporary Mathematics. (2002) 313, 85–96.
10.1090/conm/313/05370
Google Scholar
8 Chambolle A., DeVore R. A., Lee N. Y., and Lucier B. J., Nonlinear wavelet image processing: variational problems, compression, and noise removal through wavelet shrinkage, IEEE Transactions on Image Processing. (1998) 7, no. 3, 319–335, https://doi.org/10.1109/83.661182, 1669536, ZBL0993.94507.
10.1109/83.661182
PubMed Web of Science® Google Scholar
9 Beck A. and Teboulle M., A fast iterative shrinkage-thresholding algorithm for linear inverse problems, SIAM Journal on Imaging Sciences. (2009) 2, no. 1, 183–202, https://doi.org/10.1137/080716542, 2486527, ZBL1175.94009.
10.1137/080716542
Web of Science® Google Scholar
10 Hale E. T., Yin W., and Zhang Y., Fixed-point continuation for ℓ₁-minimization: methodology and convergence, SIAM Journal on Optimization. (2008) 19, no. 3, 1107–1130, https://doi.org/10.1137/070698920, 2460734.
10.1137/070698920
Web of Science® Google Scholar
11 Wen Z., Yin W., Goldfarb D., and Zhang Y., A fast algorithm for sparse reconstruction based on shrinkage, subspace optimization, and continuation, SIAM Journal on Scientific Computing. (2010) 32, no. 4, 1832–1857, https://doi.org/10.1137/090747695, 2678081, ZBL1215.49039.
10.1137/090747695
Web of Science® Google Scholar
12 Figueiredo M. A. T., Nowak R. D., and Wright S. J., Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems, IEEE Journal of Selected Topics in Signal Processing. (2007) 1, no. 4, 586–597, 2-s2.0-39449126969, https://doi.org/10.1109/JSTSP.2007.910281.
10.1109/JSTSP.2007.910281
Web of Science® Google Scholar
13 Barzilai J. and Borwein J. M., Two-point step size gradient methods, IMA Journal of Numerical Analysis. (1988) 8, no. 1, 141–148, https://doi.org/10.1093/imanum/8.1.141, 967848, ZBL0638.65055.
10.1093/imanum/8.1.141
Web of Science® Google Scholar
14 Wright S. J., Nowak R. D., and Figueiredo M. A. T., Sparse reconstruction by separable approximation, IEEE Transactions on Signal Processing. (2009) 57, no. 7, 2479–2493, https://doi.org/10.1109/TSP.2009.2016892, 2650165.
10.1109/TSP.2009.2016892
Web of Science® Google Scholar
15 Yun S. and Toh K.-C., A coordinate gradient descent method for ℓ₁-regularized convex minimization, Computational Optimization and Applications. (2011) 48, no. 2, 273–307, https://doi.org/10.1007/s10589%2D009%2D9251%2D8, 2783427.
10.1007/s10589-009-9251-8
Web of Science® Google Scholar
16 Yang J. and Zhang Y., Alternating direction algorithms for ℓ₁-problems in compressive sensing, SIAM Journal on Scientific Computing. (2011) 33, no. 1, 250–278, https://doi.org/10.1137/090777761, 2783194.
10.1137/090777761
CAS Web of Science® Google Scholar
17 Xiao Y., Wang Q., and Hu Q., Non-smooth equations based method for ℓ₁-norm problems with applications to compressed sensing, Nonlinear Analysis: Theory, Methods & Applications. (2011) 74, no. 11, 3570–3577, https://doi.org/10.1016/j.na.2011.02.040, 2803084.
10.1016/j.na.2011.02.040
Web of Science® Google Scholar
18 Zhang L. and Zhou W. J., Spectral gradient projection method for solving nonlinear monotone equations, Journal of Computational and Applied Mathematics. (2006) 196, no. 2, 478–484, https://doi.org/10.1016/j.cam.2005.10.002, 2249439, ZBL1128.65034.
10.1016/j.cam.2005.10.002
Web of Science® Google Scholar
19 Li Q. N. and Li D. H., A class of derivative-free methods for large-scale nonlinear monotone equations, IMA Journal of Numerical Analysis. (2011) 31, no. 4, 1625–1635, https://doi.org/10.1093/imanum/drq015.
10.1093/imanum/drq015
Web of Science® Google Scholar
20 Solodov M. V. and Svaiter B. F., M. Fukushima and L. Qi, A globally convergent inexact Newton method for systems of monotone equations, Reformulation: Nonsmooth, Piecewise Smooth, Semismooth and Smoothing Methods, 1998, 22, Kluwer Academic Publishers, 355–369, 1682755, ZBL0928.65059.
10.1007/978-1-4757-6388-1_18
Google Scholar
21 Zhou W. J. and Li D. H., Limited memory BFGS method for nonlinear monotone equations, Journal of Computational Mathematics. (2007) 25, no. 1, 89–96, 2292430.
Web of Science® Google Scholar
22 Zhou W. J. and Li D. H., A globally convergent BFGS method for nonlinear monotone equations without any merit functions, Mathematics of Computation. (2008) 77, no. 264, 2231–2240, https://doi.org/10.1090/S0025%2D5718%2D08%2D02121%2D2, 2429882, ZBL1203.90180.
10.1090/S0025-5718-08-02121-2
Web of Science® Google Scholar
23 Clarke F. H., Optimization and Nonsmooth Analysis, 1983, John Wiley & Sons, New York, NY, USA, 709590.
Google Scholar
24 Qi L. Q. and Sun J., A nonsmooth version of Newton′s method, Mathematical Programming A. (1993) 58, no. 3, 353–367, https://doi.org/10.1007/BF01581275, 1216791, ZBL0780.90090.
10.1007/BF01581275
Web of Science® Google Scholar
25 Chen X. and Xiang S., Computation of error bounds for P-matrix linear complementarity problems, Mathematical Programming A. (2006) 106, no. 3, 513–525, https://doi.org/10.1007/s10107%2D005%2D0645%2D9, 2216793, ZBL1134.90043.
10.1007/s10107-005-0645-9
Web of Science® Google Scholar
26 Li D. H. and Fukushima M., A modified BFGS method and its global convergence in nonconvex minimization, Journal of Computational and Applied Mathematics. (2001) 129, no. 1-2, 15–35, https://doi.org/10.1016/S0377%2D0427(00)00540%2D9, 1823208, ZBL0984.65055.
10.1016/S0377-0427(00)00540-9
Web of Science® Google Scholar

All articles

New Nonsmooth Equations-Based Algorithms for ℓ₁-Norm Minimization and Applications

Abstract

1. Introduction

2. Preliminaries

3. Algorithms and Their Convergence

4. Applications to Compressed Sensing and Image Restoration

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

New Nonsmooth Equations-Based Algorithms for ℓ1-Norm Minimization and Applications

Abstract

1. Introduction

2. Preliminaries

3. Algorithms and Their Convergence

4. Applications to Compressed Sensing and Image Restoration

Acknowledgments

References

Figures

References

Related

Information

New Nonsmooth Equations-Based Algorithms for ℓ₁-Norm Minimization and Applications