The nonlinear two-dimensional forced-convection boundary-layer magneto hydrodynamic (MHD) incompressible flow of nanofluid over a horizontal stretching flat plate with variable magnetic field including the viscous dissipation effect is solved using the homotopy perturbation method (HPM). In the present work, our results of the HPM are compared with the results of simulation using the finite difference method, Keller′s box-scheme. The comparisons of the results show that the HPM has the capability of solving the nonlinear boundary layer MHD flow of nanofluid with sufficient accuracy.

1. Introduction

Recently, lots of attention are devoted toward the semianalytical solution of real-life mathematical modeling that is inherently nonlinear differential equations with variable coefficients. Most of the nonlinear differential equations do not have an analytical solution. However, so far there have been many researchers that attempted to solve the nonlinear differential equations by using numeric methods. Using the numeric methods, a tremendous amount of CPU time as well as huge memory is required. Semianalytical methods which are more suitable than the numerical methods are applied for the solution of nonlinear nonhomogeneous partial differential equations [1–7]. Comparing with other methods, the Semianalytical methods have the advantage of simplicity when applying to solve complicated nonlinear problems. The HPM, ADM, and VIM methods are used to solve the nonhomogeneous variable coefficient partial differential equations with accurate approximation. Consequently, to extend the validity of the solution to a broader range, one needs to handle huge amount of computational effort. The most powerful Semianalytical method to the solution of nonhomogeneous variable coefficient partial differential equations is the homotopy perturbation method (HPM).

He [8–12] developed the homotopy perturbation method for solving linear, nonlinear, and initial and boundary value problems by combining the standard homotopy and the perturbation methods. The homotopy perturbation method was formulated by taking the full advantage of the standard homotopy and perturbation methods and has been modified later by some scientists to obtain more accurate results, rapid convergence, and to reduce the amount of computation [13–16].

Recently, some of researchers have solved many problems in different fields of engineering. Singh et al. [17] solved space-time fractional solidification in a finite slab with HPM. Ajadi and Zuilino [18] applied HPM to reaction-diffusion equations with source term. They concluded that rapid convergence is obtained to the exact solution by HPM. Slota [19] applied the HPM to Stefan solidification heat equation problem, and his results show that HPM is a capable method for solving the problems under consideration.

The basic motivation of this paper is to solve a two-dimensional forced-convection boundary-layer MHD problem formed by a magneto hydrodynamic (MHD) incompressible nanofluid flow in the presence of variable magnetic field over a horizontal flat plate including the viscous dissipation term using the HPM. The two-dimensional forced-convection boundary-layer MHD problem is also simulated with the numerical Keller’s box-scheme [20], and the results of simulation are compared with the results obtained by solving the problem using the HPM. In the present problem, a nanoincompressible fluid in the presence of a variable magnetic field and the viscous dissipation effect over a horizontal stretching flat plate are considered. The results are compared with the previous results of numerical simulation. To our knowledge, there have been no results reported so far for the boundary layer flow of nanofluid, using the HPM method, including the MHD with variable magnetic field, and viscous dissipation effect.

2. Basic Idea of Homotopy Perturbation Method

The homotopy perturbation method (HPM) is originally initiated by He [1–9]. This is a combination of the classical perturbation technique and homotopy technique. The basic idea of the HPM for solving nonlinear differential equations is as follows: consider the following nonlinear differential equation:

()

subject to boundary condition

()

where ℒ is a general nonlinear differential operator and B is a boundary operator.

Usually the main differential equation does not include the small parameter; however, to construct a homotopy, the nonlinear operator is divided into two parts, the first part includes the linear operator, L, and the second part includes the nonlinear operator, N. Therefore, (2.1) is rewritten as

()

We now write the homotopy that constructed by He [1–9] as follows:

()

where p is called the homotopy parameter which is usually assumed to vary between [0,1]. In (2.4), when p is equal to 1 it converts back to the main differential equation (2.1), and in case where p is equal to zero, (2.4) gives the zero-order approximation of the main differential equation (2.1). According to the perturbation method, the approximate solution to (2.4) is expressed as a series of the power of the homotopy parameter p as

()

where in the limit when p approaches 1, (2.5) becomes

()

3. Mathematical Formulation

The governing two-dimensional forced-convection boundary-layer flow over a horizontal stretching flat plate including the viscous dissipation term is written as

()

Equation (3.1) describes the continuity equation, where u and v are the velocity components in the x and y directions, respectively, (see Figure 1). Equation (3.2) describes the two-dimensional momentum equation in the presence of a variable magnetic field, where u and v are the x and y components of velocity, respectively, μ_nf and ρ_nf are the dynamic viscosity and the density of the nanofluid, respectively, σ is the electrical conductivity, and B(x) is the variable magnetic field acting in the perpendicular direction to the horizontal flat plate. Equation (3.3) describes the two-dimensional energy equation including the viscous dissipation term, where, u, v, and T are the x and y components of velocity and temperature, respectively, α_nf is the thermal diffusivity, and

is the heat capacitance of the nanofluid.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic of the physical model and coordinate system.

The boundary conditions are defined as

()

where u_w is the x-component of velocity on the horizontal flat plate, b and m are constants, and T_wand T_∞ are the plate and ambient temperatures, respectively. The nanofluid properties such as the density, ρ_nf, the dynamic viscosity, μ_nf, the heat capacitance,

, and the thermal conductivity, k_nf, are defined in terms of fluid and nanoparticles properties as in [21],

()

where ρ_f is the density of fluid, ρ_s is the density of nanoparticles, ϕ is defined as the volume fraction of the nanoparticles, μ_f is the dynamic viscosity of fluid,

is the thermal capacitance of fluid,

is the thermal capacitance of nanoparticles, and k_f and k_s are the thermal conductivities of fluid and nanoparticles, respectively.

The variable magnetic field is defined as [22, 23]

()

where B₀ and m are constant.

The following dimensionless similarity variable is used to transform the governing equations into the ordinary differential equations

()

The dimensionless stream function and dimensionless temperature are defined as

()

where the stream function ψ(x, y) is defined as

()

By applying the similarity transformation parameters, the momentum equation (3.1) and the energy equation (3.2) can be rewritten as

()

Therefore, the transformed boundary conditions are

()

The dimensionless parameters of Mn, Pr, Ec, and Re_x are the magnetic parameter, Prandtl, Eckert, and Reynolds numbers, respectively. They are defined as

()

Equation (3.10) is rewritten as

()

The boundary conditions for f and θ in (3.13) and (3.14) are as follows:

()

where coefficients, A, B, C, D, and E are written as

()

4. The HPM Applied to the Problem

We are ready now to apply the HPM to solve the similarity nonlinear ordinary differential equations (3.13) and (3.14) with boundary conditions defined as in (3.11). First we construct a homotopy for each of (3.13) and (3.14) as follows:

()

The approximation for each of f and θ in terms of the power series of homotopy parameter p is written as

()

Substituting (4.3) and (4.4) into (4.1) and (4.2), respectively, and after manipulations, the coefficients of terms of different powers for p are written as follows:

()

The above sets of recursive ordinary differential equations along with their boundary conditions are solved using the MAPLE software. Some samples of these functions obtained by the MAPLE software are brought to the reader’s attention as follows:

()

These functions, f and θ, are calculated for the case where, Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2. The physical properties of the fluid, water, and the nanoparticles, aluminum oxide (Al₂O₃), are given in Table 1.

Table 1. Thermophysical properties of water and nanoparticles.

Physical properties	Fluid (water)	Nanoparticles Al₂O₃
ρ (kg m⁻³)	997.1	3970
C_p (J kg⁻¹ K⁻¹)	4179	765
k (W m⁻¹ K⁻¹)	0.613	40

5. Numerical Method

The differential equations, (3.13) and (3.14), along with the boundary conditions, (3.15), are split into five first-order differential equations by introducing new dependent variables. The five split first-order differential equations are discretized using the first-order backward finite difference scheme, the so-called Keller’s box method [20]. The discretized form of the five split differential equations are linearized using the Newton’s method [24–26]. The discretized and linearized equations form a system of block-tridiagonal equations which are solved using the block-tridiagonal-elimination technique [26]. A step size of Δη = 0.005 is selected to satisfy the convergence criterion of 10⁻⁴ in all cases. In our simulation, η_∞ is chosen to be equal to 5 in order to suffice for taking into account the full effect of boundary layer growth. Then the differential equations, (3.13) and (3.14), along with the boundary conditions, (3.15), are solved using the HPM. The recursive differential equations with the relevant boundary conditions resulting from the HPM are solved using the MAPLE software.

6. Results and Discussions

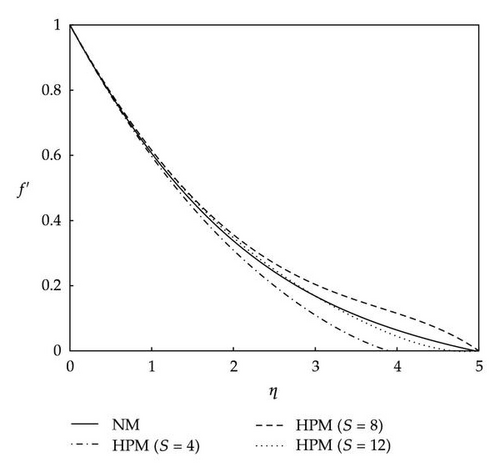
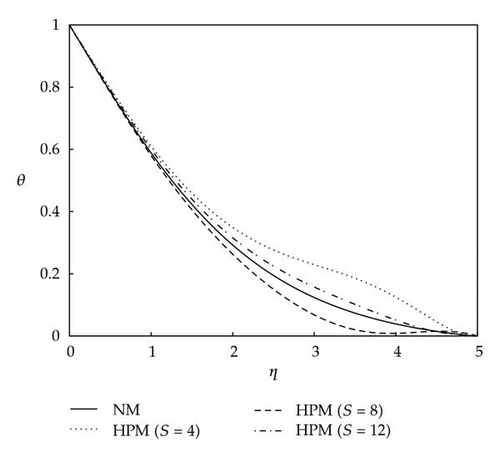
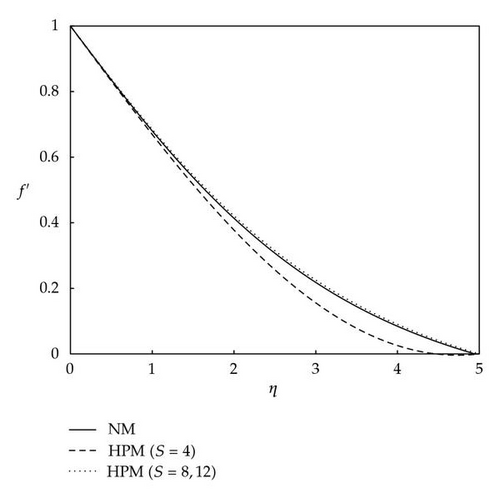
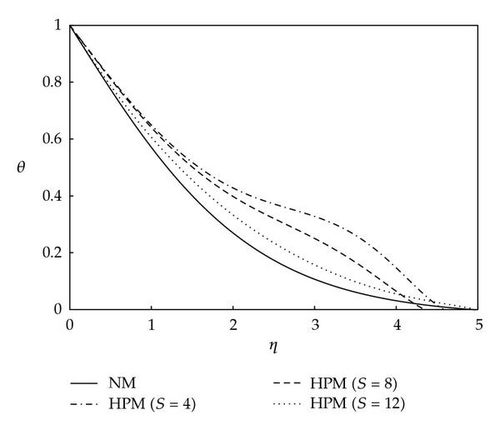
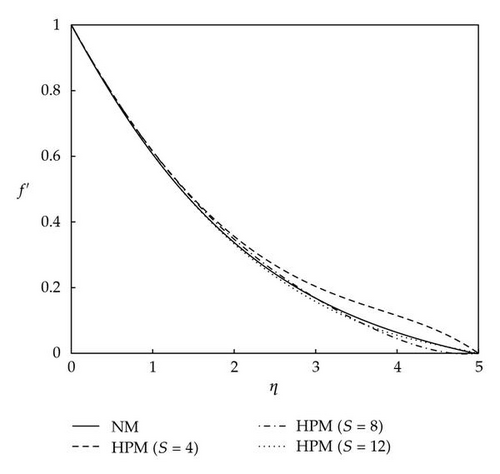
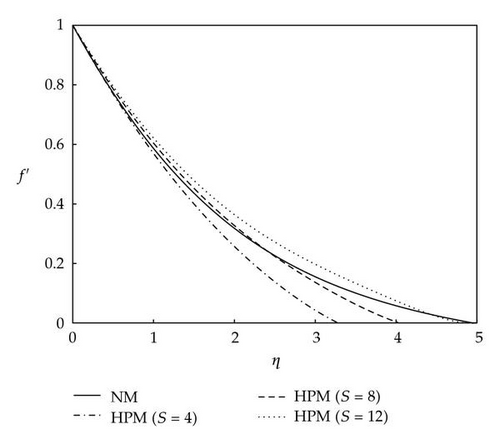
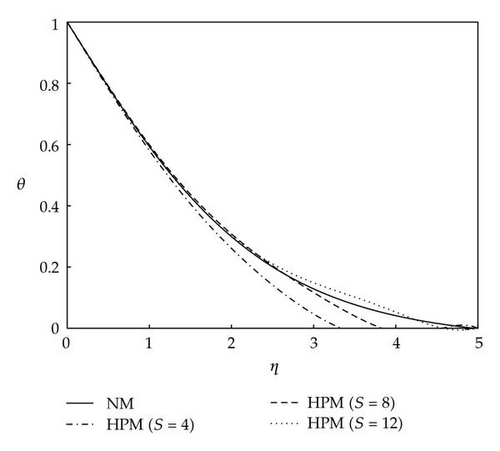
Table 2 shows the comparison between the results obtained from HPM and the results obtained from the numerical method (NM) at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2. The comparison of the results obtained from the HPM and the results obtained from the NM shows excellent agreements at different values of the similarity parameter. Figure 2 shows the comparison of dimensionless velocity profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2. The results obtained from the HPM are reported for three different sums of terms, S = 4, 8, and 12, in the HPM series solution. It is obvious from Figure 2 that as the number of sums of terms in the HPM series solution increases, the results approach towards the profile obtained from the NM. The mean discrepancies between the results of velocity obtained from the HPM for S = 12 and the results obtained from the NM are at most 2%. Figure 3 shows the comparison of dimensionless temperature profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2. The results obtained from the HPM are reported for three different sums of terms, S = 4, 8, and 12, in the HPM series solution. As the number of sums of terms in the HPM series solution increases the agreement between the results obtained from the HPM and the results obtained from the NM is more pronounced. The mean discrepancies between the results of temperature obtained from the HPM for S = 12 and the results obtained from the NM are less than 5%. Figure 4 shows the comparison of dimensionless velocity profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0. The results obtained from the HPM are reported for three different number of sums of terms, S = 4, 8, and 12, in the HPM series solution. As the number of sums of terms in the HPM series solution increases the agreement between the results of dimensionless velocity obtained from the HPM and the results obtained from the NM is more pronounced. The results of velocity obtained from the HPM for S = 8 and 12 and the results obtained from the NM are almost the same. Figure 5 shows the comparison of dimensionless temperature profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0. The results obtained from the HPM are reported for three different sums of terms, S = 4, 8, and 12, in the HPM series solution. However, as the number of sums of terms in the HPM series solution increases, the agreement between the results obtained from the HPM and the results obtained from the NM is more apparent. For the temperature profiles, the mean discrepancies between the results obtained from the HPM when S = 12 and the results obtained from the NM are at most 8%, whereas the discrepancies between the results obtained for velocity from HPM and NM are negligible at the same conditions. The reason of this behavior is due to the complex nonlinearity that exists in the nature of the governing equations which makes it so difficult to exactly realize the obsessive interaction existing in the problem. Figure 6 shows the comparison between dimensionless velocity profiles versus the normalized coordinates using the Keller’s box numerical method and the results obtained by the HPM at Ec = 0, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2. The results obtained from the HPM are reported for three different sums of terms S = 4, 8, and 12 in the HPM series solution. Figure 7 shows the comparison of dimensionless temperature profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2. The results obtained from the HPM are reported for three different sums of terms, S = 4, 8, and 12, in the HPM series solution. It is obvious that as the number of sums of terms in the HPM series solution increases, the results approach toward the profile obtained from the NM. The mean discrepancies between the results of velocity obtained from the HPM for S = 12 and the results obtained from the NM are at most 5%. Figure 8 shows the comparison between dimensionless velocity profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0.1, Pr = 6.2, φ = 0.2, and Mn = 0.2. The results obtained from the HPM are reported for three different numbers of sums of terms, S = 4, 8, and 12, in the HPM series solution. One can realize from Figure 8, as the number of sums of terms in the HPM series solution increases, the results approach toward the profile obtained from the NM. The mean discrepancies between the results of velocity obtained from the HPM for S = 12 and the results obtained from the NM are at most 5%. Figure 9 shows the comparison of dimensionless temperature profiles versus the normalized coordinates using the Keller’s box numerical method with the results obtained by the HPM at Ec = 0.1, m = 0.1, Pr = 6.2, φ = 0.2, and Mn = 0.2. The results obtained from the HPM are reported for three different numbers of sums of terms, S = 4, 8, and 12, in the HPM series solution. As the number of sums of terms in the HPM series solution increases, the results approach towards the profile obtained from the NM. The mean discrepancies between the results of velocity obtained from the HPM for S = 12 and the results obtained from the NM are at most 4%.

Table 2. Comparison between HPM and NM at Ec = 0.1, m = 0, Pr = 6.2, φ = 0.2, and Mn = 0.2.

	NM		HPM
η	f^′	θ	f^′	θ
0	1	1	1	1
0.2	0.9110	0.9134	0.911545	0.914671
0.4	0.8272	0.8276	0.827806	0.830011
0.6	0.7481	0.7442	0.748988	0.747524
0.8	0.6744	0.6643	0.675187	0.668484
1	0.606	0.5889	0.606404	0.593911
1.2	0.5427	0.5185	0.542561	0.524578
1.4	0.4844	0.4536	0.483516	0.461022
1.6	0.4309	0.3944	0.429079	0.403573
1.8	0.3819	0.3408	0.379026	0.352385
2	0.3373	0.2928	0.333116	0.307456
2.2	0.2966	0.2499	0.291102	0.268638
2.4	0.2596	0.2121	0.252741	0.235634
2.6	0.2260	0.1786	0.217807	0.207977
2.8	0.1955	0.1493	0.186097	0.185003
3	0.1679	0.1237	0.157437	0.165822
3.2	0.1428	0.1015	0.131683	0.149317
3.4	0.1202	0.0822	0.108713	0.134198
3.6	0.0994	0.0656	0.088417	0.119118
3.8	0.0806	0.0512	0.070676	0.102891
4	0.0635	0.0388	0.055326	0.084773
4.2	0.0479	0.0281	0.042121	0.064787
4.4	0.0336	0.0130	0.030677	0.043964
4.6	0.0205	0.0112	0.020429	0.024391
4.8	0.0085	0.0044	0.010565	0.008861
5	0	0	0	0

7. Conclusions

In this work, the nonlinear two-dimensional forced-convection boundary-layer magneto hydrodynamic (MHD) incompressible flow of nanofluid over a horizontal stretching flat plate with variable magnetic field including the viscous dissipation effect is solved using the homotopy perturbation method (HPM). The results are justified and compared with the results obtained from the numerical method (NM). Our results obtained from the HPM, when the number of sums of terms in the HPM series solution increases, showed a monotonic convergence towards the results using the NM. The results obtained from the HPM show at most less than 8% mean deviations when compared with the results obtained from the NM. For the nonlinear MHD problem, this is encouraging because these results are only achieved by including at most S = 12 number of sums of terms in the HPM series solution.

Nomenclature

B(x):: Magnetic field
b:: Constant parameter
Ec:: Eckert number
:: Thermal capacitance of solid
:: Thermal capacitance of fluid
f:: Dimensionless velocity variable
k_s:: Thermal conductivity of nanoparticles
k_f:: Thermal conductivity of fluid
m:: Index of power law velocity
Mn:: Magnetic parameter
Pr:: Prandtl number
Re:: Reynolds number
S:: No. of terms in the HPM
T:: Absolute temperature
T_∞:: Constant temperature of the fluid far away from the plate
T_w:: Given temperature at the plate
u:: Velocity in x-direction
v:: Velocity in y-direction
u_w:: Velocity of the plate
x:: Horizontal coordinate
y:: Vertical coordinate.
Greek Symbols: σ:: Electrical conductivity
θ:: Dimensionless temperature
ψ:: Stream function
μ_f:: Fluid viscosity
φ:: Nanoparticles volume fraction
ρ_s:: nanoparticles density
ρ_f:: Fluid density.

References

1 He J. H., Non-perturbative methods for strongly nonlinear problems [Ph.D. thesis], 2006, de-Verlag im Internet GmbH, Berlin, Germany.
Google Scholar
2 He J.-H., Some asymptotic methods for strongly nonlinear equations, International Journal of Modern Physics B. (2006) 20, no. 10, 1141–1199, https://doi.org/10.1142/S0217979206033796, 2220565, ZBL1102.34039.
10.1142/S0217979206033796
Web of Science® Google Scholar
3 He J.-H., Homotopy perturbation method for solving boundary value problems, Physics Letters A. (2006) 350, no. 1-2, 87–88, 2199322, https://doi.org/10.1016/j.physleta.2005.10.005, ZBL1195.65207.
10.1016/j.physleta.2005.10.005
CAS Web of Science® Google Scholar
4 He J. H., Application of homotopy perturbation method to nonlinear wave equations, Chaos, Solitons & Fractals. (2005) 26, no. 3, 695–700, 2-s2.0-18844426016, https://doi.org/10.1016/j.chaos.2005.03.006.
10.1016/j.chaos.2005.03.006
Web of Science® Google Scholar
5 He J.-H., Approximate analytical solution for seepage flow with fractional derivatives in porous media, Computer Methods in Applied Mechanics and Engineering. (1998) 167, no. 1-2, 57–68, 1665221, https://doi.org/10.1016/S0045-7825(98)00108-X, ZBL0942.76077.
10.1016/S0045-7825(98)00108-X
Web of Science® Google Scholar
6 He J. H., Approximate solution of nonlinear differential equations with convolution product nonlinearities, Computer Methods in Applied Mechanics and Engineering. (1998) 167, no. 1-2, 69–73, 2-s2.0-0032308350.
10.1016/S0045-7825(98)00109-1
Web of Science® Google Scholar
7 He J. H., Variational iteration method—a kind of non-linear analytical technique: some examples, International Journal of Non-Linear Mechanics. (1999) 34, no. 4, 699–708, 2-s2.0-0000092673.
10.1016/S0020-7462(98)00048-1
Web of Science® Google Scholar
8 He J.-H., Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering. (1999) 178, no. 3-4, 257–262, 1711041, https://doi.org/10.1016/S0045-7825(99)00018-3, ZBL0956.70017.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
9 He J.-H., A coupling method of a homotopy technique and a perturbation technique for non-linear problems, International Journal of Non-Linear Mechanics. (2000) 35, no. 1, 37–43, 1723761, https://doi.org/10.1016/S0020-7462(98)00085-7.
10.1016/S0020-7462(98)00085-7
Web of Science® Google Scholar
10 He J.-H. and Wu X.-H., Construction of solitary solution and compacton-like solution by variational iteration method, Chaos, Solitons & Fractals. (2006) 29, no. 1, 108–113, 2213340, https://doi.org/10.1016/j.chaos.2005.10.100, ZBL1147.35338.
10.1016/j.chaos.2005.10.100
Web of Science® Google Scholar
11 He J.-H., Periodic solutions and bifurcations of delay-differential equations, Physics Letters A. (2005) 347, no. 4-6, 228–230, 2176126, https://doi.org/10.1016/j.physleta.2005.08.014, ZBL1195.34116.
10.1016/j.physleta.2005.08.014
CAS Web of Science® Google Scholar
12 He J. H., Limit cycle and bifurcation of nonlinear problems, Chaos, Solitons & Fractals. (2005) 26, no. 3, 827–833, 2-s2.0-18844391045, https://doi.org/10.1016/j.chaos.2005.03.007.
10.1016/j.chaos.2005.03.007
Web of Science® Google Scholar
13 He J. H., Homotopy perturbation method for bifurcation of nonlinear problems, International Journal of Nonlinear Sciences and Numerical Simulation. (2005) 6, no. 2, 207–208, 2-s2.0-17844387391.
10.1515/IJNSNS.2005.6.2.207
Web of Science® Google Scholar
14 Ariel P. D., Hayat T., and Asghar S., Homotopy perturbation method and axisymmetric flow over a stretching sheet, International Journal of Nonlinear Sciences and Numerical Simulation. (2006) 7, no. 4, 399–406, 2-s2.0-33748924289.
10.1515/IJNSNS.2006.7.4.399
Web of Science® Google Scholar
15 Ganji D. D. and Hashemi Kachapi S. H., Analysis of nonlinear equations in fluids, Progress in Nonlinear Science. (2011) 2, 1–293.
Google Scholar
16 Ganji D. D. and Hashemi Kachapi S. H., Analytical and Numerical Methods in Engineering and Applied Sciences, Progress in Nonlinear Science. (2011) 3, 1–579.
Google Scholar
17 Singh J., Gupta P. K., Rai K. N., and CIMS-DST, Homotopy perturbation method to space-time fractional solidification in a finite slab, Applied Mathematical Modelling. Simulation and Computation for Engineering and Environmental Systems. (2011) 35, no. 4, 1937–1945, https://doi.org/10.1016/j.apm.2010.11.005, 2763831, ZBL1217.80153.
10.1016/j.apm.2010.11.005
Google Scholar
18 Ajadi S. O. and [email protected], Zuilino M., Approximate analytical solutions of reaction-diffusion equations with exponential source term: homotopy perturbation method (HPM), Applied Mathematics Letters. (2011) 24, no. 10, 1634–1639, https://doi.org/10.1016/j.aml.2011.04.003.
10.1016/j.aml.2011.04.003
Web of Science® Google Scholar
19 Slota D., The application of the homotopy perturbation method to one-phase inverse Stefan problem, International Communications in Heat and Mass Transfer. (2010) 37, no. 6, 587–592, 2-s2.0-77953542087, https://doi.org/10.1016/j.icheatmasstransfer.2010.03.009.
10.1016/j.icheatmasstransfer.2010.03.009
Web of Science® Google Scholar
20 Keller H. B., A new difference scheme for parabolic problems, Numerical Solution of Partial Differential Equations, II, 1971, Academic Press, New York, NY, USA, 327–350, 0277129, ZBL0243.65060.
10.1016/B978-0-12-358502-8.50014-1
Google Scholar
21 Aminossadati S. M. and Ghasemi B., Natural convection cooling of a localised heat source at the bottom of a nanofluid-filled enclosure, European Journal of Mechanics, B. (2009) 28, no. 5, 630–640, 2-s2.0-67749139444, https://doi.org/10.1016/j.euromechflu.2009.05.006.
10.1016/j.euromechflu.2009.05.006
Web of Science® Google Scholar
22 Chiam T. C., Hydromagnetic flow over a surface stretching with a power-law velocity, International Journal of Engineering Science. (1995) 33, no. 3, 429–435, 2-s2.0-0029250454.
10.1016/0020-7225(94)00066-S
CAS Web of Science® Google Scholar
23 Devi S. P. A. and Thiyagarajan M., Steady nonlinear hydromagnetic flow and heat transfer over a stretching surface of variable temperature, Heat and Mass Transfer. (2006) 42, no. 8, 671–677, 2-s2.0-33646423855, https://doi.org/10.1007/s00231-005-0640-y.
10.1007/s00231-005-0640-y
Web of Science® Google Scholar
24 Cebeci T. and Bradshaw P., Momentum Transfer in Boundary Layers, 1997, Hemisphere Publishing Corporation, New York, NY, USA.
Google Scholar
25 Cebeci T. and Bradshaw P., Physical and Computational Aspects of Convective Heat Transfer, 1988, Springer-Verlag, New York, NY, USA, Springer Study Editions, 969366.
10.1007/978-1-4612-3918-5
Google Scholar
26 Salleh M. Z., Ahmad S., and Nazar R., Numerical solutions of the forced convection boundary layer flow at a forward stagnation point, European Journal of Scientific Research. (2008) 19, no. 4, 644–653, 2-s2.0-53649104156.
Google Scholar

Citing Literature

All articles

The HPM Applied to MHD Nanofluid Flow over a Horizontal Stretching Plate

Abstract

1. Introduction

2. Basic Idea of Homotopy Perturbation Method

3. Mathematical Formulation

4. The HPM Applied to the Problem

5. Numerical Method

6. Results and Discussions

7. Conclusions

Nomenclature

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The HPM Applied to MHD Nanofluid Flow over a Horizontal Stretching Plate

Abstract

1. Introduction

2. Basic Idea of Homotopy Perturbation Method

3. Mathematical Formulation

4. The HPM Applied to the Problem

5. Numerical Method

6. Results and Discussions

7. Conclusions

Nomenclature

References

Citing Literature

Figures

References

Related

Information