Application of the Homotopy Perturbation Method for Solving the Foam Drainage Equation
Abstract
We use homotopy perturbation method (HPM) to handle the foam drainage equation. Foaming occurs in many distillation and absorption processes. The drainage of liquid foams involves the interplay of gravity, surface tension, and viscous forces. The concept of He′s homotopy perturbation method is introduced briefly for applying this method for problem solving. The results of HPM as an analytical solution are then compared with those derived from Adomian′s decomposition method (ADM) and the variational iteration method (VIM). The results reveal that the HPM is very effective and convenient in predicting the solution of such problems, and it is predicted that HPM can find a wide application in new engineering problems.
1. Introduction
Most scientific problems and physical phenomena occur nonlinearly. Except in a limited number of these problems, finding the exact analytical solutions of such problems are rather difficult. Therefore, there have been attempts to develop new techniques for obtaining analytical solutions which reasonably approximate the exact solutions [1]. In recent years, several such techniques have drawn special attention, such as Hirota’s bilinear method [2], the homogeneous balance method [3, 4], inverse scattering method [5], Adomian’s decomposition method (ADM) [6, 7], the variational iteration method (VIM) [8, 9], and homotopy analysis method (HAM) [10] as well as homotopy perturbation method (HPM).
The homotopy perturbation method was established by He [11]. The method has been used by many authors to handle a wide variety of scientific and engineering applications to solve various functional equations. In this method, the solution is considered as the sum of an infinite series, which converges rapidly to accurate solutions. Recently, considerable research work has been conducted in applying this method to the linear and nonlinear equations [12–25].
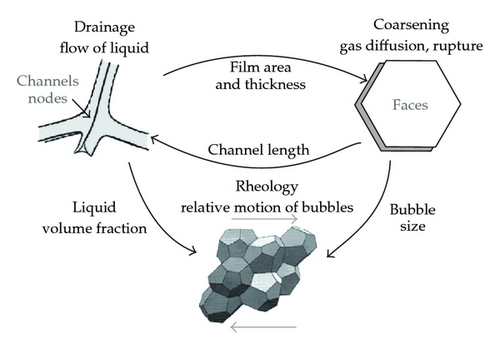
The pursuit of analytical solutions for foam drainage equation is of intrinsic scientific interest. To the best of the authors’ knowledge, there is no paper that has solved the nonlinear foam drainage equation by HPM. In this paper, the basic idea of HPM is described, and then, it is applied to study the following nonlinear foam drainage equation [49]. Finally, the results of HPM as an analytical solution are then compared with those derived from Adomian’s decomposition method [49] and the variational iteration method [50].
2. Basic Idea of Homotopy Perturbation Method
3. Implementation of HPM
4. Results and Discussion
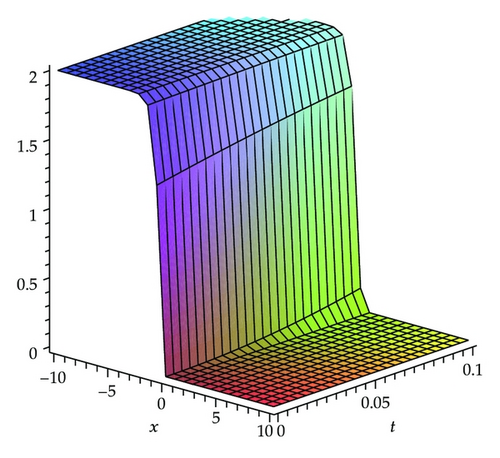
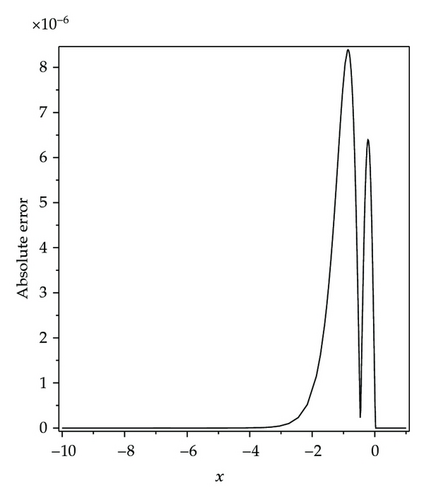
In this section, we present the results with HPM to show the efficiency of the method, described in the previous section for solving (1.1). By Figures 2, 3, and 4, we may simply compare the HPM solution and exact solution of (1.1) for c = 1, respectively. It is easy to verify the accuracy of the obtained results if we graphically compare HPM solutions with the exact ones. The absolute error of HPM is drawn in Figure 5 at t = 0.01. It can be seen from this figure that the absolute error is very small and the mentioned method is very accurate. The effect of velocity of the wave, c, is demonstrated in Figure 6.
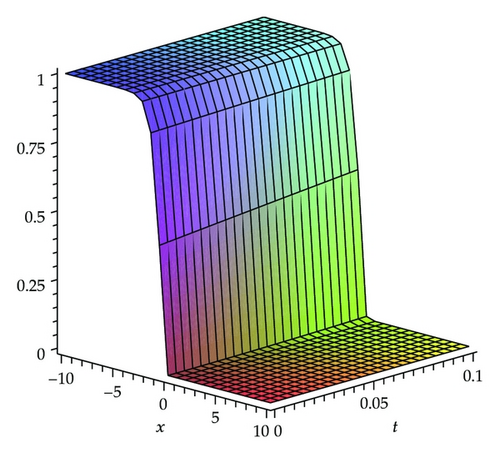
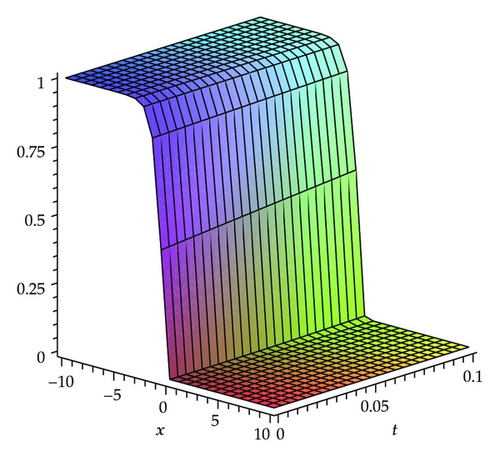
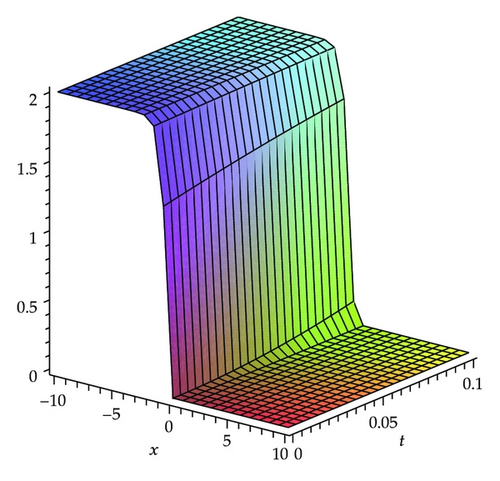
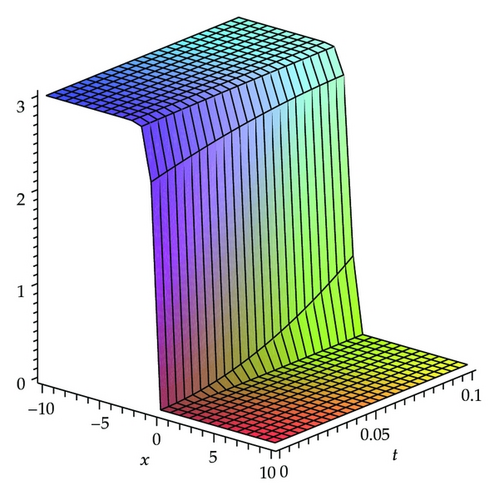
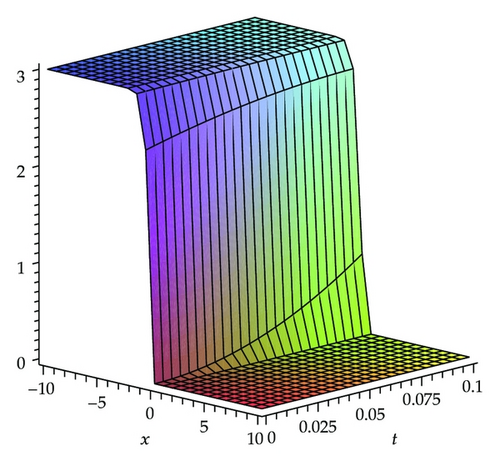
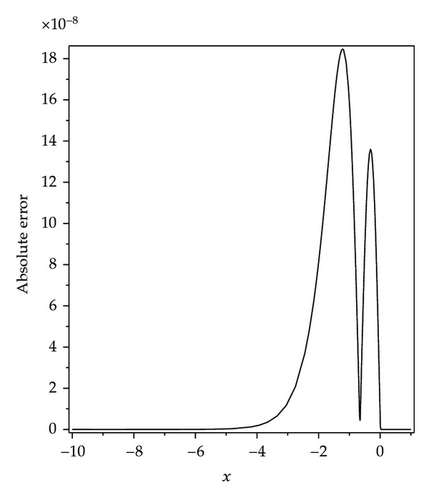

It is important to see the difference between the results obtained by ADM [49] and VIM [50] and the results which are obtained by the analytic solution using by the HPM. These can be seen by comparing Tables 1, 2, and 3. The results which are obtained by the HPM and the exact solutions are quite similar. It is shown the accuracy of the HPM. The solution of the HPM is more accurate than the ADM. While using HPM, the difficulty of calculating Adomian′s polynomials does not occur. Another benefit of using the HPM is that the time consumption of the numerical calculation is less than the time consumption of ADM.
5. Conclusion
In this work, He’s homotopy perturbation method has been successfully utilized to derive approximate explicit analytical solution for the nonlinear foam drainage equation. The results show that this perturbation scheme provides excellent approximations to the solution of this nonlinear equation with high accuracy and avoids linearization and physically unrealistic assumptions. This new method is extremely simple, easy to apply, needs less computation, and accelerates the convergence to the solutions. The results obtained here are compared with results of exact solution. The current work illustrates that the HPM is indeed a powerful analytical technique for most types of nonlinear problems and several such problems in scientific studies and engineering may be solved by this method.
Acknowledgments
The authors gratefully acknowledge the support of the Department of Mechanical Engineering and the talented office of Semnan University for funding the current research grant.




