We consider the spatial numerical range of operators on weighted Hardy spaces and give conditions for closedness of numerical range of compact operators. We also prove that the spatial numerical range of finite rank operators on weighted Hardy spaces is star shaped; though, in general, it does not need to be convex.

1. Introduction

For a bounded linear operator T on a Hilbert space ℋ, the numerical range W(T) is the image of the unit sphere of ℋ under the quadratic form x ↦ 〈Tx, x〉 associated with the operator. More precisely,

(1.1)

Let X be a complex normed space with dual apace X^*. The Banach algebra of all bounded linear operators is denoted by L(X). For an operator T ∈ L(X), the spatial numerical range V(T) of T is defined by

(1.2)

When X is a Hilbert space, ∥x∥ = ∥x^*∥ = 〈x, x^*〉 if and only if x^* is the function given by x^*(y) = 〈y, x〉(y ∈ X). Thus, V(T) in this case coincides with classical W(T). The algebra numerical range is defined by

(1.3)

The notion of numerical range or the classical field of values was first introduced by O. Toeplitz in 1918 for matrices. This concept was independently extended by G. Lumer and F. Bauer in the sixties to a bounded linear operator on an arbitrary Banach space. In 1975, Lightbourne and Martin [1] extended this concept by employing a class of seminorms generated by a family of supplementary projections.

In [2], Gaur and Husain have studied the spatial numerical range of elements of Banach algebras without identity. Specifically, the relationship between spatial numerical ranges, numerical ranges, and spectra has been investigated. Among other results, it has been shown that the closure of the spatial numerical range of an element of a Banach algebra without identity but with regular norm is exactly its numerical range as an element of the unitized algebra.

A complete survey on numerical ranges of operators can be found in the books by Bonsall and Duncan [3, 4]; we refer the reader to these books for general information and background.

In Section 2, after giving some background material, we give useful formula for the spatial numerical range of operators on weighted Hardy space. In Section 3, we show that the spatial numerical range of an operator needs not to be convex, and we also prove that the spatial numerical range of finite rank operators is star shaped. Finally, in Section 4, we give conditions for closedness of numerical range of compact operators.

2. Preliminaries

Let X be a complex normed space with dual space X^*. The mapping [·, ·] : X × X → ℂ is called a semi-inner product on X if the following properties are satisfied:

(i)
[x + y, z] = [x, z]+[y, z] for all x, y, z ∈ X,
(ii)
[λx, y] = λ[x, y] for all x, y ∈ X and λ ∈ ℂ,
(iii)
[x, x] ≥ 0 for all x ∈ X,
(iv)
|[x, y]|² ≤ [x, x][y, y] for all x, y ∈ X and λ ∈ ℂ.

In [5], Lumer defined the concept of a semi-inner product on X and showed that every normed linear space (X, ∥·∥) has at least one semi-inner product [·, ·], such that

(2.1)

In terms of a semi-inner product satisfying (2.1), the definition of usual numerical range for Hilbert space operator at once generalizes to give the definition of the numerical range W(T) for a linear operator on X,

(2.2)

In most cases, there are infinitely many semi-inner products on X satisfying (2.1); however, Lumer proved that

, the closed convex hull of W(T), is independent of the choice of semi-inner product satisfying (2.1). In fact, Lumer showed that

depends only on the norms of the operators.

The unit ball of X is called smooth if for all x, with ∥x∥ = 1, there is a unique x^* ∈ X^*, such that ∥x^*∥ = 1 and 〈x, x^*〉 = 1. In this case, there is a unique semi-inner products on X satisfying (2.1), and then V(T) coincides with numerical range W(T) corresponding to the unique semi-inner product satisfying (2.1).

A principal result in spatial numerical range is a Theorem of Williams that gives

, where σ(T) is the spectrum of T. Also we have (see [3])

(i)
W(T)⊆V(T),
(ii)
,
(iii)
sup {|λ | : λ ∈ W(T)} = sup {|λ | : λ ∈ V(T)}.

It is of course trivial that every eigenvalue of T is actually in V(T).

Let 1 < p < ∞ and {β(n)} _n be a sequence of positive numbers with β(0) = 1. The weighted Hardy space, which is denoted by H^p(β), is the set of all formal power series

with

(2.3)

Let μ(K) = ∑_n∈Kβ(n) ^p, for K⊆ℕ ∪ {0}. Then μ is a σ-finite measure and H^p(β) = L^p(μ). So, the space H^p(β) is reflexive Banach space with the norm

, and the dual of H^p(β) is H^q(β^p/q), where 1/p + 1/q = 1 and β^p/q = {β(n) ^p/q} [6].

In the case p = 2, the weighted Hardy spaces with β(n) = 1, β(n) = (n + 1) ^(−1/2), and β(n) = (n + 1) ^1/2 are classical Hardy space, Bergman space, and the Dirichlet space, respectively. The space H²(β) becomes a Hilbert space with inner product

(2.4)

where f(z) = ∑a_nzⁿ and g(z) = ∑b_nzⁿ are the elements of H²(β) [7].

The notation 〈f, g〉 is to stand for g(f), where f ∈ H^p(β) and g ∈ (H^p(β)) ^*. Note that

(2.5)

For f ∈ H^p(β) and g ∈ H^q(β^p/q), with f(z) = ∑a_nzⁿ and g(z) = ∑b_nzⁿ, we define f^* and ^*g by f^*(z) = ∑|a_n|^p−1sgn (a_n)zⁿ and ^*g(z) = ∑|b_n|^q−1sgn (b_n)zⁿ, respectively, where for a nonzero complex number w, sgn (w) = (w/|w|) and sgn (0) = 0. Clearly,

(2.6)

So, f^* ∈ H^q(β^p/q) and ^*g ∈ H^p(β). Obviously, one can see that ^*(f^*) = f for all f ∈ H^p(β) and (^*g) ^* = g for all g in (H^p(β)) ^*. By a simple computation, we also have the following consequences:

(a)
if α ≥ 0 and f ∈ H^p(β), then (αf) ^* = α^p−1f^*,
(b)
if f ∈ H^p(β), .

We define a semi-inner product on H^p(β) by

(2.7)

where f, g ∈ H^p(β) and F_f : = ∥f∥^2−pf^*. Obviously, we have

Lemma 2.1. If T is a bounded linear operator on H^p(β), then

(2.8)

where W(T) is the numerical range of T with respect to the semi-inner product defined by (2.7).

Proof. Suppose that f ∈ H^p(β), g ∈ (H^p(β)) ^*, ∥f∥ = ∥g∥ = 1, and 〈f, g〉 = 1. Then

(2.9)

So, equality occurs in Holder inequality, and hence there are complex numbers α and η (independent of n), such that

and

(see [8]). Hence,

. But

(2.10)

and hence

. On the other hand,

(2.11)

Therefore,

, or equivalently

. Hence,

, or g = f^*. Then, the unit ball of H^p(β) is smooth, and so there is one and only one semi-inner product on H^p(β) which satisfy (2.1). Then, V(T) = W(T) [3]. The last equality can be proved in a similar way as the first part of this proof, and so we omit it.

3. Shape of the Spatial Numerical Range

The usual numerical range of a bounded linear operator on a Hilbert space is convex, and for every bounded linear operator T on a normed space X, we know that V(L(X), T) is convex. Although V(T) needs not to be convex (see [3]), B. E. Cain and H. Schneider proved that it is connected. Also in [9], Kuliyev proved that the spatial numerical range of a given operator on a separable Banach space is pathwise connected.

Recall that V(T) is star shaped with respect to zero if tz ∈ V(T) for 0 ≤ t ≤ 1 and z ∈ V(T).

In Theorem 3.1, we give a necessary and sufficient condition for the numerical range of a bounded linear operator to be star shaped. In Example 3.2, we show that the spatial numerical range of linear operator T on H^p(β) needs not to be convex, even if T is compact (see also [3]). We also determine the shape of V(T), when T is a finite rank operator. Finally, in Theorem 3.3, we prove that there is an operator T on H^p(β) that may not be star shaped.

Theorem 3.1. Let T be a bounded linear operator on H^p(β). Then

(a)
V(T) is star shaped with respect to zero if and only if
(3.1)
(b)
if T is finite rank on H^p(β) and 0 ∈ V(T), then V(T) is star shaped with respect to zero.

Proof. The proof is trivial, as 〈T(kf), (kf) ^*〉 = k^p〈Tf, f^*〉, for each nonnegative real number k and f ∈ H^p(β).

Example 3.2. Let β(1) = 1 and T be the linear operator on H^p(β) given by

(3.2)

Therefore,

(3.3)

where

and

. By writing

, we have

(3.4)

Now, let

(3.5)

We have α > β unless p = 2. If

(3.6)

then the conjugate of z is

(3.7)

and so V(T) ^* = V(T). Thus, α was attained at points above and below the real axis, and we have concluded that V(T) is not convex unless p = 2. In Figure 1, we draw the shape of V(T), for p = 3.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

V(T) for p = 3.

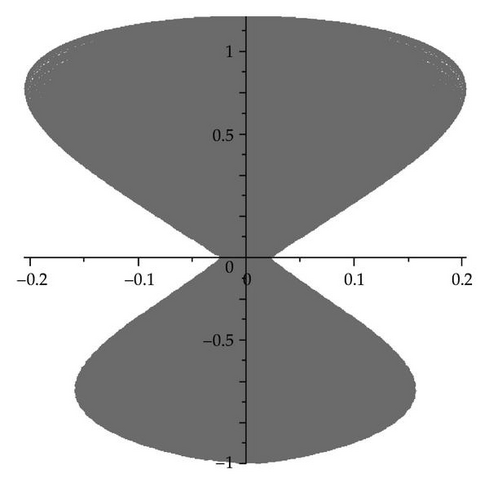
Theorem 3.3. There is an operator T on H^p(β) with 0 ∈ V(T), such that V(T) is not star shaped.

Proof. We proof this theorem by contradiction. Suppose that the spatial numerical range of each linear operator that allowed origin is star shaped. If a, z ∈ V(T), then 0 ∈ V(T − a), and so t(z − a) ∈ V(T − a) for 0 ≤ t ≤ 1. Hence, tz + (1 − t)a ∈ V(T), and it follows that V(T) is convex which is a contradiction to the previous example.

4. Compact Operators

Since H²(β) is a Hilbert space, the numerical range of a compact operator on H²(β) is closed if and only if it contains the origin. Also the numerical range of a compact operator on H^p(β) contains all nonzero extreme points of its closure, and since H^p(β) is infinite dimensional, there is a compact operator T on H^p(β), such that V(T) is not closed (see [10] and page 103-109 of [11]). So, in general, the spatial numerical range of a compact operator needs not to be closed. In the following theorem, we give a closedness condition of such operators.

Theorem 4.1. Let T be a compact operator on H^p(β). If V(T) is star shaped with respect to zero, then it is closed.

Proof. Since V(T) is star shaped with respect to zero, then by Theorem 3.1,

(4.1)

For given , there is a sequence h_n with ∥h_n∥_p = 1 and . By reflexivity of H^p(β) and Alaogul′s Theorem, there is a sequence , such that in weak topology and in weak* topology for some h ∈ ball(H^p(β)) and g ∈ ball((H^p(β)) ^*).

Now, let m ∈ ℕ. Define the bounded linear functionals x, x^* by

(4.2)

respectively, on (H^p(β)) ^* and H^p(β). Hence,

(4.3)

as k → ∞. Then,

(4.4)

as k → ∞. But by definition

. Therefore,

or g = h^*.

On the other hand,

(4.5)

Since T is completely continuous and

weakly, then

, and hence

. So, α = 〈Th, h^*〉, and the proof is complete by using (4.1).

Since in infinite dimensional spaces 0 is allowed in spectrum of any compact operator, then we have the following corollary.

Corollary 4.2. Let T be a compact operator on H^p(β), such that V(T) is convex. Then V(T) is closed if and only if 0 ∈ V(T).

Acknowledgments

The authors would like to thank Professor Alexander Rosa, the Editor-in-Chief of the International Journal of Mathematics and Mathematical Sciences, and the referee for useful and helpful comments and suggestions.

References

1 Lightbourne,J. H.III and MartinR. H.Jr., Projection seminorms and the field of values of linear operators, Numerische Mathematik. (1975) 24, no. 2, 151–161, 0410414, https://doi.org/10.1007/BF01400964, ZBL0323.47003.
10.1007/BF01400964
Web of Science® Google Scholar
2 Gaur A. K. and Husain T., Spatial numerical ranges of elements of Banach algebras, International Journal of Mathematics and Mathematical Sciences. (1989) 12, no. 4, 633–640, https://doi.org/10.1155/S0161171289000785, 1024965, ZBL0719.46025.
10.1155/S0161171289000785
Google Scholar
3 Bonsall F. F. and Duncan J., Numerical Ranges of Operators on Normed Spaces and of Elements of Normed Algebras, 1971, 2, Cambridge University Press, London, UK, London Mathematical Society Lecture Note Series, 0288583, ZBL0207.44802.
10.1017/CBO9781107359895
Google Scholar
4 Bonsall F. F. and Duncan J., Numerical Ranges. II, 1973, Cambridge University Press, New York, NY, USA, London Mathematical Society Lecture Notes Series, no. 1, 0442682, ZBL0271.46039.
10.1017/CBO9780511662515
Google Scholar
5 Lumer G., Semi-inner-product spaces, Transactions of the American Mathematical Society. (1961) 100, 29–43, 0133024, https://doi.org/10.1090/S0002-9947-1961-0133024-2, ZBL0102.32701.
10.1090/S0002-9947-1961-0133024-2
Google Scholar
6 Seddighi K., Hedayatiyan K., and Yousefi B., Operators acting on certain Banach spaces of analytic functions, International Journal of Mathematics and Mathematical Sciences. (1995) 18, no. 1, 107–110, https://doi.org/10.1155/S0161171295000147, 1311579, ZBL0821.47022.
10.1155/S0161171295000147
Google Scholar
7 Shields A. L., Weighted shift operators and analytic function theory, Topics in Operator Theory, 1974, American Mathematical Society, Providence, RI, USA, 49–128, Math. Surveys, no. 13, 0361899, ZBL0303.47021.
10.1090/surv/013/02
Google Scholar
8 Kuptsov L. P., M. Hazewinkel, Hölder inequality, Encyclopaedia of Mathematics, 2001, Kluwer Academic Publishers, Dordrecht, The Netherlands.
Google Scholar
9 Kuliyev T. Y., Pathwise connectivity of the spatial numerical range, Proceedings of the American Mathematical Society. (1994) 122, no. 4, 1173–1174, https://doi.org/10.2307/2161187, 1211582, ZBL0817.47003.
10.1090/S0002-9939-1994-1211582-1
Web of Science® Google Scholar
10 de Barra G., Giles J. R., and Sims B., On the numerical range of compact operators on Hilbert spaces, Journal of the London Mathematical Society. (1972) 5, 704–706, 0315495, https://doi.org/10.1112/jlms/s2-5.4.704, ZBL0244.47012.
10.1112/jlms/s2-5.4.704
Web of Science® Google Scholar
11 Sims B., On numerical range and its application to Banach algebra, Ph.D. thesis, 1972, School of Mathematical and Physical Sciences, University of Newcastle.
Google Scholar

All articles

Spatial Numerical Range of Operators on Weighted Hardy Spaces

Abstract

1. Introduction

2. Preliminaries

3. Shape of the Spatial Numerical Range

4. Compact Operators

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Spatial Numerical Range of Operators on Weighted Hardy Spaces

Abstract

1. Introduction

2. Preliminaries

3. Shape of the Spatial Numerical Range

4. Compact Operators

Acknowledgments

References

Figures

References

Related

Information