Asymptotic Analysis of Transverse Magnetic Multiple Scattering by the Diffraction Grating of Penetrable Cylinders at Oblique Incidence
Abstract
We have presented a derivation of the asymptotic equations for transverse magnetic multiple scattering coefficients of an infinite grating of penetrable circular cylinders for obliquely incident plane electromagnetic waves. We have first deducted an “Ansatz” delineating the asymptotic behavior of the transverse magnetic multiple scattering coefficients associated with the most generalized condition of oblique incidence (Kavaklıoğlu, 2000) by exploiting Schlömilch series corresponding to the special circumstance that the grating spacing is much smaller than the wavelength of the incident electromagnetic radiation. The validity of the asymptotic equations for the aforementioned scattering coefficients has been verified by collating them with the Twersky′s asymptotic equations at normal incidence. Besides, we have deduced the consequences that the asymptotic forms of the equations at oblique incidence acquired in this paper reduce to Twersky′s asymptotic forms at normal incidence by expanding the generalized scattering coefficients at oblique incidence into an asymptotic series as a function of the ratio of the cylinder radius to the grating spacing.
1. Introduction
Rayleigh [1] first treated the problem of the incidence of plane electric waves on an insulating dielectric cylinder as long ago as 1881. He published the classical electromagnetic problem of the diffraction of a plane wave at normal incidence by a homogeneous dielectric cylinder [2]. His solution was later generalized for obliquely incident plane waves when the magnetic vector of the incident wave is transverse to the axis of the cylinder by Wait [3]. Moreover, Rayleigh [4, 5] adduced the first theoretical investigation for the problem of diffraction by gratings. His results have been extended by Wait [6] for the treatment of scattering of plane waves by parallel-wire grids with arbitrary angle of incidence. Wait [6] developed the solution of the problem of the scattering of plane electromagnetic waves incident upon a parallel-wire grid that was backed by a plane-conducting surface. He generalized this result subsequently to a plane wave, incident obliquely with arbitrary polarization on a planar grid [7]. Wait did not treat the scattering of obliquely incident plane electromagnetic waves by the infinite array of thick dielectric cylinders. This configuration has recently been studied by Kavaklıoğlu [8–10], and an analytic expression for the generalized multiple scattering coefficients of the infinite grating at oblique incidence was captured in the form of a convergent infinite series [11].
The formal analytical solution for the scattering of a plane acoustic or electromagnetic wave by an arbitrary configuration of parallel cylinders of different radii and physical parameters in terms of cylindrical wave functions was obtained by Twersky [12] who considered all possible contributions to the excitation of a particular cylinder by the radiation scattered by the remaining cylinders in the grating and extended this solution to expound the case where all the axes of cylinders lie in the same plane [13]. Twersky [14] subsequently introduced the formal multiple scattering solution of a plane wave by an arbitrary configuration of parallel cylinders to the finite grating of cylinders. He later employed Green’s function methods to represent the multiple scattering amplitude of one cylinder within the grating in terms of the functional equation and the single-scattering amplitude of an isolated cylinder [15]. Furthermore, Twersky [16] acquired a set of algebraic equations for the multiple scattering coefficients of the infinite grating in terms of the elementary function representations of Schlömilch series [17] and the well-known scattering coefficients of an isolated cylinder.
In the area of acoustics, Millar [18] studied the problem of scattering of a plane wave by finite number of cylinders equispaced in a row that are associated with scatterers both “soft” and “hard” in the acoustical sense. The solutions in the form of series in powers of a small parameter, essentially the ratio of cylinder dimension to wavelength, were obtained. Besides, Millar [19] investigated the scattering by an infinite grating of identical cylinders. In a more recent investigation, Linton and Thompson [20] formulated the diffracted acoustic field by an infinite periodic array of circles and determined the conditions for resonance by employing the expressions which enable Schlömilch series to be computed accurately and efficiently [21–23].
Previous investigations mentioned above do not include the most general case of oblique incidence although the grating is illuminated by an incident plane E-polarized electromagnetic wave at an arbitrary angle ϕi to the x-axis, whereas in the generalized oblique incidence solution presented in this investigation, the direction of the incident plane wave makes an arbitrary oblique angle θi with the positive z-axis as indicated in Figure 1. As far as can be ascertained by the writers, Sivov [24, 25] first treated the diffraction by an infinite periodic array of perfectly conducting cylindrical columns for the most generalized case of obliquely incident plane-polarized electromagnetic waves in order to determine the reflection and transmission coefficients of the infinite grating of perfectly conducting cylinders in free space under the assumption that the period of the grating spacing was small compared to a wavelength. The configuration of a greater relevance to the problem has recently been investigated by many other researchers. For instance, Lee [26] studied the scattering of an obliquely incident electromagnetic wave by an arbitrary configuration of parallel, nonoverlapping infinite cylinders and acquired the solution for the scattering of an obliquely incident plane wave by a collection of closely spaced radially stratified parallel cylinders that can have an arbitrary number of stratified layers [27]. Moreover, Lee [28] presented a general treatment of scattering of arbitrarily polarized incident light by a collection of radially stratified circular cylinders at oblique incidence, described the solution to the problem of scattering of obliquely incident light by a closely spaced parallel radially stratified cylinders embedded in a semi-infinite dielectric medium [29], and developed a general scattering theory for obliquely incident plane-polarized monochromatic waves on a finite slab containing closely spaced radially stratified circular cylinders [30]. In addition, the formulation for the extinction and scattering cross-sections of closely spaced parallel infinite cylinders in a dielectric medium of finite thickness is presented [31]. In the area of modeling photonic crystal structures, Smith et al. [32] developed a formulation for cylinder gratings in conical incidence using a multipole method and studied scattering matrices and Bloch modes in order to investigate the photonic band gap properties of woodpile structures [33]. This area of research has recently received a lot of attention due to potential applications to microcircuitry, nanotechnology, and optical waveguides.
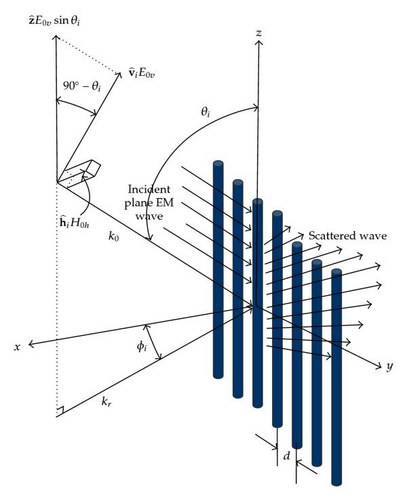
Three-dimensional generalization of Twersky’s solution [15, 16] for scattering of waves by the infinite grating of dielectric circular cylinders was originally developed by Kavaklıoğlu [8–10] by employing the separation-of-variables method for both TM and TE polarizations, and the reflected and transmitted fields were derived for obliquely incident plane H-polarized waves in [34]. Kavaklıoğlu and Schneider [35] presented the asymptotic solution of the multiple scattering coefficients for obliquely incident and vertically polarized plane waves as a function of the ratio of the cylinder radius to grating spacing when the grating spacing, d, is small compared to a wavelength.
Furthermore, Kavaklıoğlu and Schneider [11] acquired the exact analytical solution for the multiple scattering coefficients of the infinite grating for obliquely incident plane electromagnetic waves by the application of the direct Neumann iteration technique to two infinite sets of equations describing the exact behavior of the multiple scattering coefficients, which was originally published in [8, 10], in the form of a convergent infinite series and obtained the generalized form of Twersky’s functional equation for the infinite grating in matrix form for obliquely incident waves [11].
The purpose of this paper is to elucidate the derivation of the equations pertaining to the asymptotic behavior of the transverse magnetic multiple scattering coefficients of an infinite array of infinitely long circular dielectric cylinders illuminated by obliquely incident plane electromagnetic waves. The arbitrarily polarized obliquely incident plane wave depicted in Figure 1 can be decomposed into two different modes of polarization. The asymptotic representation associated with the transverse magnetic (TM) mode that is also defined as vertical polarization, for which the incident electric field Einc has a component parallel to the constituent cylinders of the grating, will be treated in this investigation.
2. Problem Formulation
“An infinite number of infinitely long identical dielectric circular cylinders,” which are separated by a distance “d,” are placed parallel to each other in the y-z plane and positioned perpendicularly to the x-y plane as indicated in Figure 1. For TM mode; is the unit vector associated with the vertical polarization and has a component parallel to the cylinders of the grating. The fact that “the incident E-field has a component parallel to all the cylinders of the dielectric grating” does not mean that we deal with the TM mode as it does not exclude the existence of other components of E-field. The incident plane wave depicted in Figure 1 makes an angle of obliquity θi with the positive z-axis.
Lemma 2.1 (multiple scattering representation for an infinite grating of dielectric circular cylinders for obliquely incident E-polarized plane electromagnetic waves [3, 7, 8]). A vertically polarized plane electromagnetic wave, which is obliquely incident upon the infinite array of identical insulating dielectric circular cylinders with radius “a,” dielectric constant “εr,” and relative permeability “μr,” can be expanded in “the individual cylindrical coordinate system (Rs, ϕs, z) of the sth cylinder” in terms of the cylindrical waves referred to the axis of sth cylinder as
Lemma 2.2 (expressions for the z-components of the exterior fields [8]). Let for all n ∈ Z, where “Z” stands for the set of all integers, denote the set of all multiple scattering coefficients corresponding to the exterior electric and magnetic fields of the infinite grating associated with obliquely incident plane E-polarized electromagnetic waves, respectively. Then, the exterior electric and magnetic field intensities associated with vertically polarized obliquely incident plane electromagnetic waves are given as
3. Derivation of the Asymptotic Equations for the Multiple Scattering Coefficients of the Infinite Grating at Oblique Incidence
This section is devoted to the formal derivation of the asymptotic equations for the exterior electric and magnetic multiple scattering coefficients of the infinite grating of dielectric cylinders for obliquely incident vertically polarized plane waves. Since the wavelength of the incident radiation is much larger than the grating spacing, the condition max {(krd/2π)(1 ± sin ψi)} ≡ krd/π < krd ≪ 1 is automatically satisfied thereby excluding any special case associated with the grazing modes. In order to demonstrate the procedure of obtaining the asymptotic equations for the TM multiple scattering coefficients of the infinite grating at oblique incidence, we will first introduce the exact equations corresponding to the transverse magnetic multiple scattering coefficients associated with the exterior electric and magnetic fields of the infinite grating of dielectric circular cylinders at oblique incidence by asserting the following lemma.
Lemma 3.1 (exact equations of the transverse magnetic multiple scattering coefficients of the infinite grating of insulating dielectric cylinders at oblique incidence [8]). Exact equations corresponding to the transverse magnetic multiple scattering coefficients of an infinite grating of insulating dielectric cylinders associated with obliquely incident plane electromagnetic waves are first presented by the equations (85a) and (85b) in [8] as
Theorem 3.2 (approximate equations for the scattering coefficients of the infinite grating at oblique incidence when krd ≪ 1). The asymptotic form of the exact equations for the transverse magnetic multiple scattering coefficients of an infinite grating at oblique incidence can be inferred by two different sets, in which the first one contains only the odd coefficients and the second set contains only the even coefficients. Odd multiple scattering coefficients associated with the infinite grating of dielectric circular cylinders at oblique incidence satisfy the following two sets of asymptotic equations:
Proof. The exact equations in (3.1) can be solved for An, and when the distance between the cylinders of the infinite grating is smaller than the wavelength of the incident wave, that is, for krd ≪ 1 the exact equations take the following form:
The elementary function representations of the Schlömilch series ℐn(krd) in (2.5b) have originally been derived by Twersky [17] for the normal incidence and modified by Kavaklıoğlu [10] for the oblique incidence. We will employ these elementary function representations for the evaluation of the asymptotic forms of the Schlömilch series ℋn = 𝒥n + i𝒩n in the limit of krd ≪ 1. Twersky’s forms [16, 17] are still valid for the case of obliquely incident waves [10] with a slight modification in their arguments.
Lemma 3.3 (approximate expressions for the “Schlömilch series ℋn = 𝒥n + i𝒩n” in the limit of krd ≪ 1 [10, 17]). We have obtained ℋ0 for the special case of n = 0 as
Remark 3.4 (Bessel series 𝒥0, 𝒥2n, and 𝒥2n+1). The propagating range of the Schlömilch series ℋn, for all n ∈ Z+, where Z+ = {0,1, 2,3, …} in (3.17) and ((3.21), is described by “𝒥n” Bessel series, which can explicitly be written as
Remark 3.5 (Neumann series 𝒩0, 𝒩2n, and 𝒩2n+1). The evanescent range of the Schlömilch series ℋn, for all n ∈ Z+ in (3.17) and (3.21), is described by “i𝒩n” where 𝒩n is known as the Neumann series. 𝒩n in (3.17) and ((3.21) can be put into the following form for this limiting case (krd ≪ 1) as
Remark 3.6 (special case when μ+ = μ− = 0). The physical problem under consideration corresponds to the special case for which there is only one propagating mode and the scattering of wavelengths is larger than the grating spacing, that is, (krd/2π)(1 ± sin ψi) < 1. Then the Bessel series for ϕ0 = π + ψi, which implies that the plane wave is incident onto the grating in the first quadrant, for all n ∈ Z+, reduces to
Remark 3.7 (approximations for Neumann series𝒩0, 𝒩2n, and 𝒩2n+1 in the limit of Δ ≪ 1). Inserting μ+ = μ− = 0 in (3.23a), (3.23b), and (3.23c), the expression for 𝒩0 in (3.23a)) reduces to
Remark 3.8 (approximations for Schlömilch series, ℋn = 𝒥n + i𝒩n in the limit of Δ ≪ 1). If krd is small, that is to say if (krd/2π)(1 ± sin ψi) < 1, then there is only one discrete propagating mode. Employing the expansions for the Bessel and Neumann Series obtained in the previous sections for ϕ0 = π + ψi; the Schlömilch Series in this range can be expressed as
Remark 3.9 (leading terms of the Schlömilch series, ℋn = 𝒥n + i𝒩n in the limit of Δ ≪ 1). The leading terms of ℋ’s for large “n”, for all n ∈ N is given as
4. Asymptotic Expansions for the Scattering Coefficients of the Infinite Grating at Oblique Incidence in the Limiting Case of “(a/d) ≪ 1”
Theorem 4.1 (asymptotic equations for the multiple scattering coefficients corresponding to the exterior electric and magnetic field intensities associated with obliquely incident vertically polarized plane electromagnetic waves). The multiple scattering coefficients corresponding to the exterior electric and magnetic field intensities associated with obliquely incident vertically polarized plane electromagnetic waves satisfy two infinite sets of asymptotic equations described by
Proof. We have defined the overall effect of the multiple scattering terms when the wavelength is much larger than the grating spacing, that is, (krd) ≪ 1, and (kra/krd) ≡ ξ < 1/2 as
5. Discussion and Comparison of the Generalized Transverse Magnetic Multiple Scattering Coefficients of the Infinite Grating with Twersky’s Normal Incidence Case
Remark 5.1 (Twersky’s asymptotic solution for the multiple scattering coefficients at normal incidence). The exact equations for the multiple scattering coefficients of the infinite grating associated with the vertically polarized normally incident waves [16] can be solved by truncation as
Lemma 5.2 (generalized asymptotic solution of the multiple scattering coefficients at oblique incidence [11, 34, 35]). The generalized asymptotic solution for the multiple scattering coefficients of an infinite grating of dielectric circular cylinders for obliquely incident vertically polarized waves has already been acquired in [35] by solving the asymptotic matrix equations of the infinite grating at oblique incidence as
Twersky’s asymptotic solution for the transverse magnetic multiple scattering coefficients of the infinite grating at normal incidence can then be acquired by exploiting the generalized asymptotic equations at oblique incidence derived in this investigation, thereby verifying the validity of the proposed “Ansatz” in Section 4.
Remark 5.3 (reduction of the generalized asymptotic solution at oblique incidence to Twersky’s asymptotic solution for the multiple scattering coefficients at normal incidence). In order to reduce Twersky’s results at normal incidence from the generalized multiple scattering coefficients at oblique incidence given in (5.22a)–(5.25b), we have used ψi = 0, θi = π/2, sin θi = 1, and F = 0 in (5.22a)–(5.25b) and acquired the following results: (a) a comparison of (5.22a), which determines the generalized scattering coefficient for n = 0, with (5.4a) and (5.13a) proves that the generalized multiple scattering coefficient at oblique incidence reduces to the Twersky’s coefficient for the normal incidence case; (b) the following term, namely, , which represents the wavelength-independent part of the (1,1) element of the scattering matrix in (3.10)), reduces to the Twersky’s an,0 for the normal incidence case as
6. Conclusion
In this investigation, we have presented a rigorous derivation of the asymptotic equations associated with the multiple scattering coefficients of an infinite grating of dielectric circular cylinders for obliquely incident vertically polarized plane electromagnetic waves. We have predicted the asymptotic behavior of the multiple scattering coefficients of the infinite grating at oblique incidence when the wavelength of the incident radiation is much larger than the distance between the constituent cylinders of the grating, that is, (dsin θi)(1 ± sin ψi) ≪ λ0 ≡ 2π/k0. Furthermore, we have predicated that our results are nothing but the generalizations of those acquired by [16] for the nonoblique incidence case. We have inferred that these equations can be solved by a technique described by Kavaklıoğlu and Schneider [35], which reduces to Twersky’s asymptotic solution at normal incidence, as well.




