We construct a new type of q-Euler numbers and polynomials with weak weight α : , , respectively. Some interesting results and relationships are obtained. Also, we observe the behavior of roots of the q-Euler numbers and polynomials with weak weight α. By means of numerical experiments, we demonstrate a remarkably regular structure of the complex roots of q-Euler polynomials with weak weight α.

1. Introduction

The Euler numbers and polynomials possess many interesting properties are arising in many areas of mathematics and physics. Recently, many mathematicians have studied the area of the q-Euler numbers and polynomials (see [1–19]). In this paper, we construct a new type of q-Euler numbers and polynomials with weak weight α. The main purpose of this paper is also to investigate the zeros of the q-Euler polynomials with weak weight α. Furthermore, we give a table for the zeros of the q-Euler numbers and polynomials with weak weight α.

Throughout this paper we use the following notations. By ℤ_p we denote the ring of p-adic rational integers, ℚ_p denotes the field of p-adic rational numbers, ℂ_p denotes the completion of algebraic closure of ℚ_p, ℕ denotes the set of natural numbers, ℤ denotes the ring of rational integers, ℚ denotes the field of rational numbers, ℂ denotes the set of complex numbers, and ℤ₊ = ℕ ∪ {0}. Let ν_p be the normalized exponential valuation of ℂ_p with

. When one talks of q-extension, q is considered in many ways such as an indeterminate, a complex number q ∈ ℂ, or p-adic number q ∈ ℂ_p. If q ∈ ℂ one normally assume that |q | < 1. If q ∈ ℂ_p, we normally assume that |q − 1|_p < p^−1/(p−1) so that q^x = exp (xlog q) for |x|_p ≤ 1. Throughout this paper we use the notation

()

(cf. [1–11, 15–18]). Hence, lim _q→1[x] _q = x for any x with |x|_p ≤ 1 in the present p-adic case. For

()

the fermionic p-adic q-integral on ℤ_p is defined by Kim as follows:

()

(cf. [3–6]). If we take g₁(x) = g(x + 1) in (1.3), then we easily see that

()

From (1.4), we obtain

()

where g_n(x) = g(x + n) (cf. [3–6]).

As well-known definition, the Euler polynomials are defined by

()

with the usual convention of replacing Eⁿ(x) by E_n(x). In the special case, x = 0, E_n(0) = E_n are called the nth Euler numbers (cf. [1–11]).

Our aim in this paper is to define q-Euler numbers and polynomials with weak weight α. We investigate some properties which are related to q-Euler numbers and polynomials with weak weight α. We also derive the existence of a specific interpolation function which interpolates q-Euler numbers and polynomials with weak weight α at negative integers. Finally, we investigate the behavior of roots of the q-Euler polynomials with weak weight α.

2. Basic Properties for q-Euler Numbers and Polynomials with Weak Weight α

Our primary goal of this section is to define q-Euler numbers and polynomials with weak weight α. We also find generating functions of q-Euler numbers and polynomials with weak weight α.

For α ∈ ℤ and q ∈ ℂ_p with |1 − q|_p ≤ 1, q-Euler numbers

are defined by

()

By using p-adic q-integral on ℤ_p, we obtain

()

By (2.1), we have

()

We set

()

By using above equation and (2.2), we have

()

Thus q-Euler numbers with weak weight α,

are defined by means of the generating function

()

By using (2.1), we have

()

By (2.5), (2.7), we have

()

Next, we introduce q-Euler polynomials

with weak weight α. The q-Euler polynomials

with weak weight α are defined by

()

By using p-adic q-integral, we obtain

()

We set

()

By using (2.10) and (2.11), we obtain

()

Obverse that if q → 1, then

and

Since [x + y] _q = [x] _q + q^x[y] _q, we easily obtain that

()

Observe that if q → 1, then and .

By (2.10), we have the following complement relation.

Theorem 2.1 (property of complement). One has

()

By (2.10), we have the following distribution relation.

Theorem 2.2 (distribution relation). For any positive integer m(=odd), one has

()

By (1.5), (2.1), and (2.9), we easily see that

()

Hence, we have the following theorem.

Theorem 2.3. Let m ∈ ℤ₊. If n ≡ 0(mod 2), then

()

If n ≡ 1(mod 2), then

()

From (1.4), one notes that

()

Therefore, we obtain the following theorem.

Theorem 2.4. For n ∈ ℤ₊, one has

()

By Theorem 2.4 and (2.13), we have the following corollary.

Corollary 2.5. For n ∈ ℤ₊, one has

()

with the usual convention of replacing

By (2.12), one has

()

Hence we have the following difference equation.

Theorem 2.6 (difference equation). For n ∈ ℤ₊, one has

()

Using q-Euler numbers and polynomials with weak weight α, q-Euler zeta function with weak weight α and Hurwitz q-Euler zeta functions with weak weight α are defined. These functions interpolate the q-Euler numbers and q-Euler polynomials with weak weight α, respectively. In this section we assume that q ∈ ℂ with |q | < 1. From (2.6), we note that

()

Using the above equation, we are now ready to define q-Euler zeta functions.

Definition 2.7. Let s ∈ ℂ.

()

Note that is a meromorphic function on ℂ. Note that, if q → 1, then which is the Euler zeta functions. Relation between and is given by the following theorem.

Theorem 2.8. For k ∈ ℕ, one has

()

Observe that function interpolates numbers at nonnegative integers. By using (2.12), we note that

()

By (2.27) and (2.28), we are now ready to define the Hurwitz q-Euler zeta functions.

Definition 2.9. Let s ∈ ℂ. Then, one has

()

Note that is a meromorphic function on ℂ. Obverse that, if q → 1, then which is the Hurwitz Euler zeta functions. Relation between and is given by the following theorem.

Theorem 2.10. For k ∈ ℕ, one has

()

Observe that

function interpolates

numbers at nonnegative integers.

3. Distribution and Structure of the Zeros

In this section, we assume that α ∈ ℕ and q ∈ ℂ, with |q | < 1. We observe the behavior of roots of the q-Euler polynomials . We display the shapes of the q-Euler polynomials , and we investigate the zeros of the q-Euler polynomials . We plot the zeros of the q-Euler polynomials for n = 10,20,30,40 and x ∈ ℂ (Figure 1). In Figure 1 (top-left), we choose n = 10, q = 1/2, and α = 3. In Figure 1 (top-right), we choose n = 20, q = 1/2, and α = 3. In Figure 1 (bottom-left), we choose n = 30, q = 1/2, and α = 3. In Figure 1 (bottom-right), we choose n = 40, q = 1/2, and α = 3.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

.

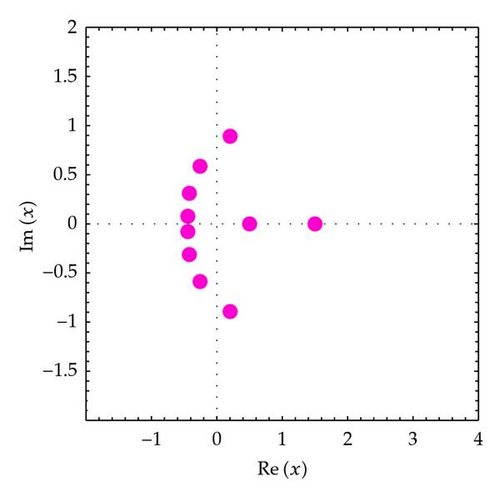
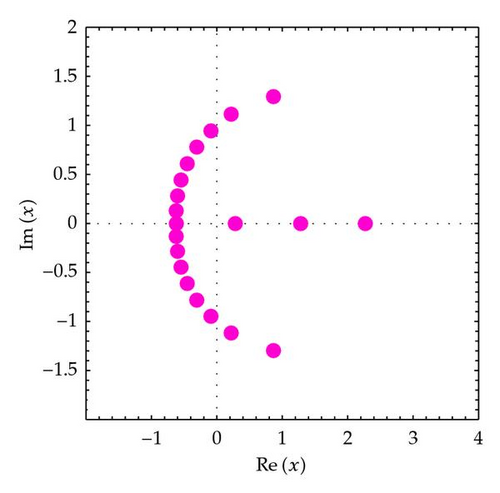
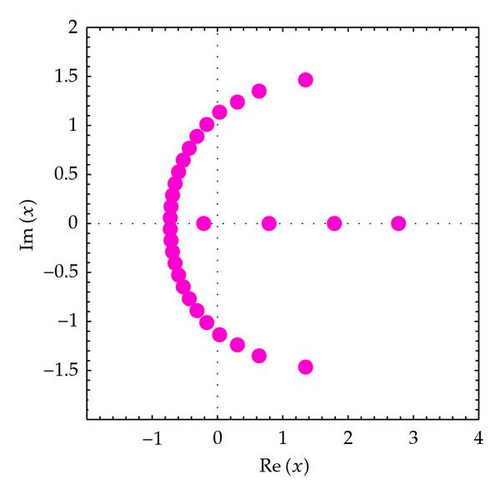
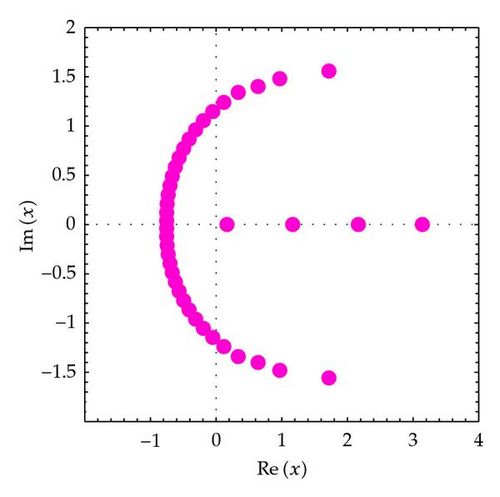
In order to understand zeros behavior better, we present Figures 2 and 3. We plot the zeros of (Figure 2).

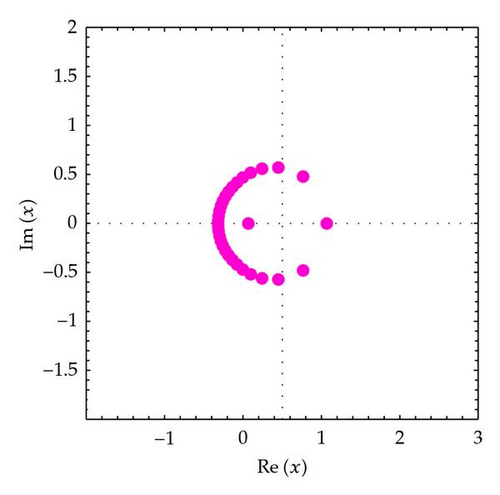
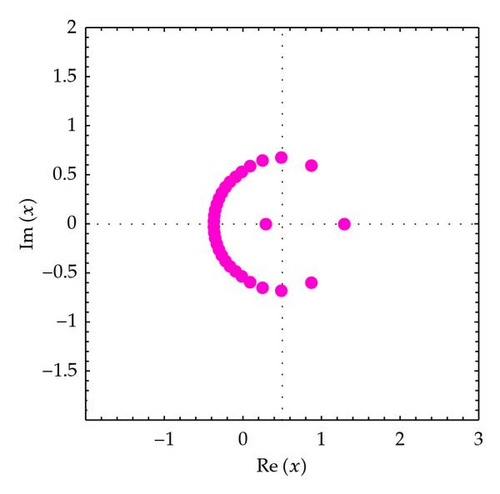
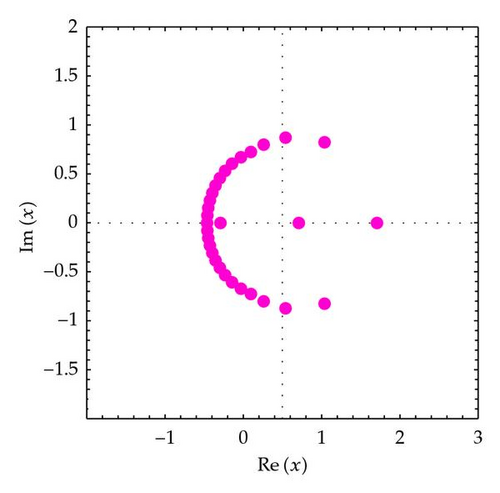
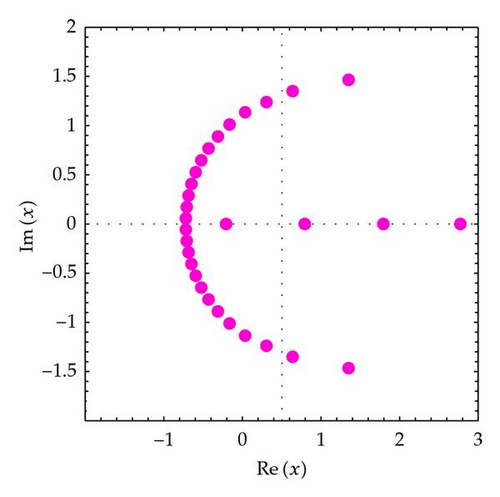
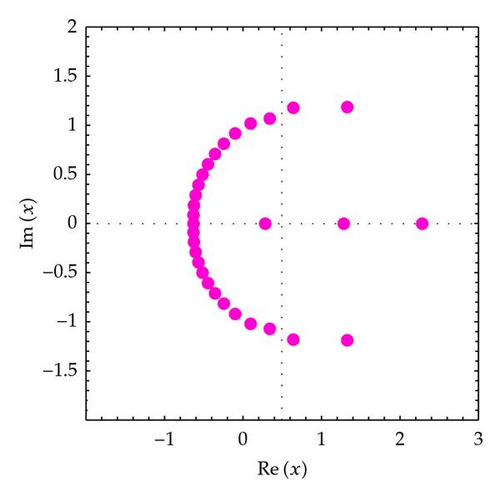
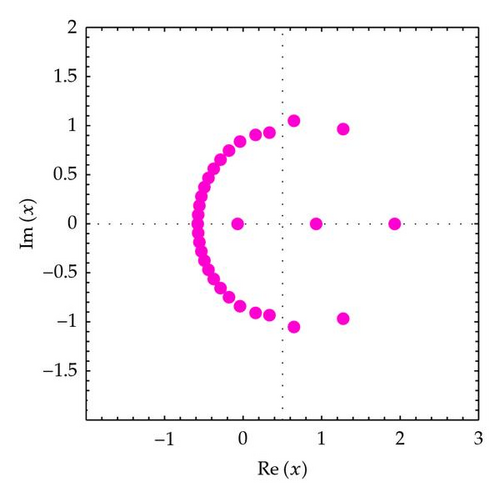
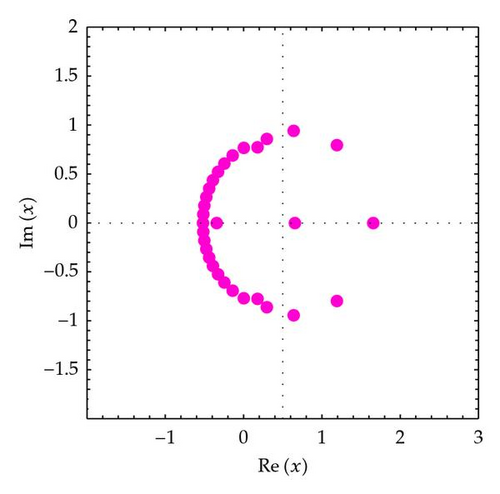
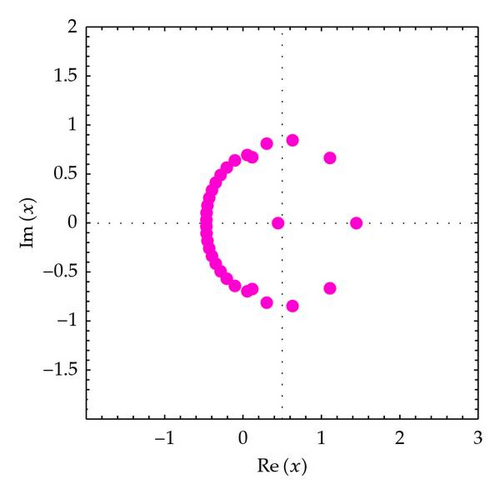
In Figure 2 (top-left), we choose n = 30, q = 1/5, and α = 3. In Figure 2 (top-right), we choose n = 30, q = 1/4, and α = 3. In Figure 2 (bottom-left), we choose n = 30, q = 1/3, and α = 3. In Figure 2 (bottom-right), we choose n = 30, q = 1/2, and α = 3.

We plot the zeros of the q-Euler polynomials for n = 30, q = 1/2, α = 5,7, 9,11 and x ∈ ℂ (Figure 3).

In Figure 3 (top-left), we choose n = 30, q = 1/2, and α = 5. In Figure 3 (top-right), we choose n = 30, q = 1/2, and α = 7. In Figure 3 (bottom-left), we choose n = 30, q = 1/2, and α = 9. In Figure 3 (bottom-right), we choose n = 30, q = 1/2, and α = 11.

Our numerical results for approximate solutions of real zeros of the q-Euler polynomials , are displayed (Tables 1 and 2).

Table 1. Numbers of real and complex zeros of

	α = 3		α = 5
Degree n	Real zeros	Complex zeros	Real zeros	Complex zeros
1	1	0	1	0
2	2	0	2	0
3	1	2	1	2
4	2	2	2	2
5	3	2	1	4
6	2	4	2	4
7	3	4	3	4
8	2	6	2	6
9	3	6	3	6
10	2	8	2	8
11	3	8	3	8
12	4	8	2	10
13	3	10	3	10

Table 2. Approximate solutions of

Degree n	x
1	0.0824622
2	−0.176174, 0.301704
3	0.513012
4	−0.220226, 0.701301
5	−0.306596, −0.132473, 0.868839
6	0.0191767, 1.01918
7	−0.41178, 0.155365, 1.15534
8	0.279948, 1.27971
⋮	⋮

Next, we calculated an approximate solution satisfying the q-Euler polynomials . The results are given in Table 2.

We observe a remarkably regular structure of the complex roots of the q-Euler polynomials . We hope to verify a remarkably regular structure of the complex roots of the q-Euler polynomials (Table 1). This numerical investigation is especially exciting because we can obtain an interesting phenomenon of scattering of the zeros of the q-Euler polynomials . These results are used not only in pure mathematics and applied mathematics, but also in mathematical physics and other areas.

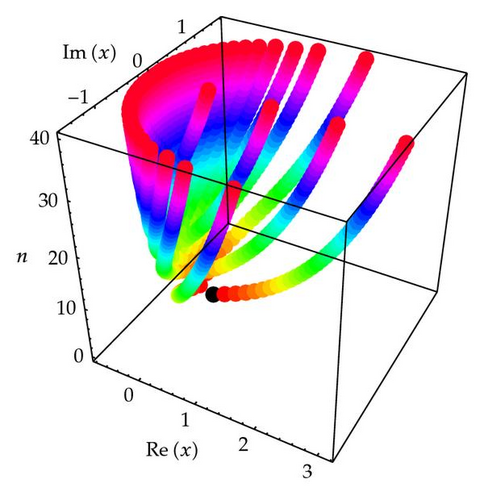
Stacks of zeros of for q = 1/2, 1 ≤ n ≤ 30 from a 3D structure are presented (Figure 4).

We present the distribution of real zeros of the q-Euler polynomials for q = 1/2, 1 ≤ n ≤ 30 (Figure 5).

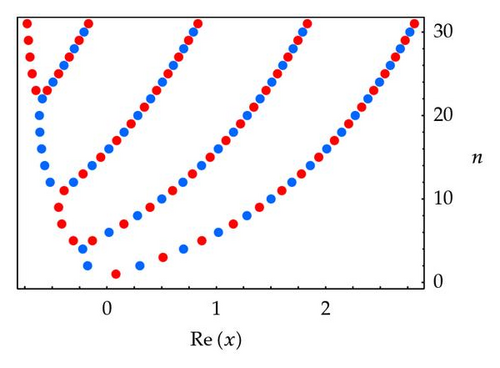
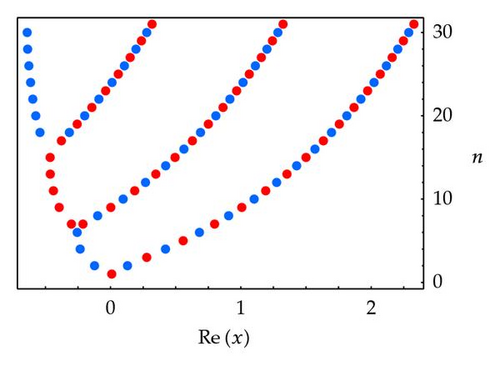
In Figure 5 (left), we choose α = 3. In Figure 3 (right), we choose α = 5.

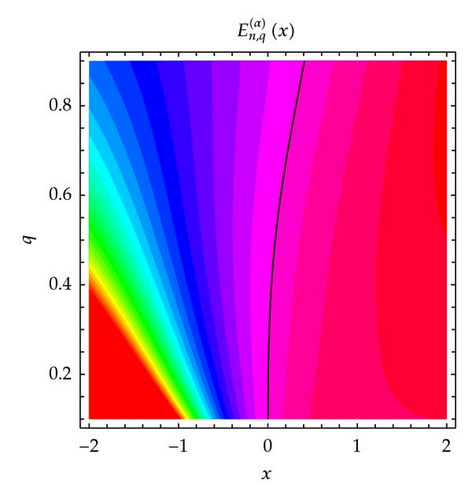
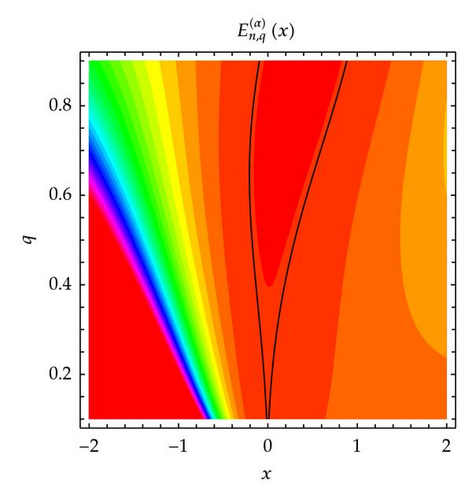
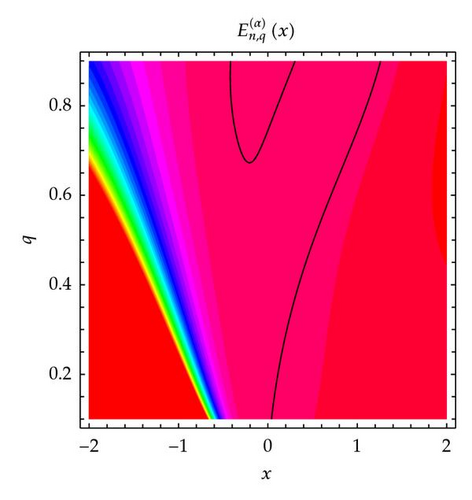
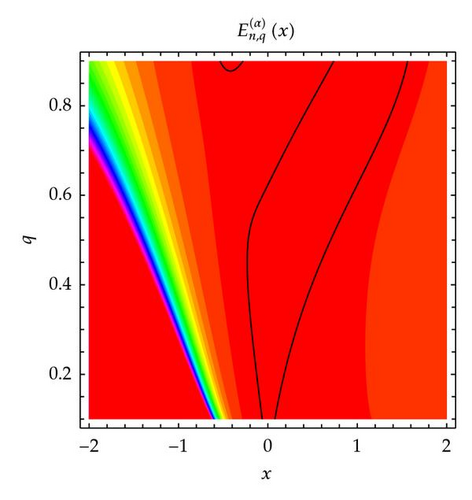
The plot above shows for real 1/10 ≤ q ≤ 9/10 and −2 ≤ x ≤ 2, with the zero contour indicated in black (Figure 6). In Figure 6 (top-left), we choose n = 1 and α = 3. In Figure 6 (top-right), we choose n = 2 and α = 3. In Figure 6 (bottom-left), we choose n = 3 and α = 3. In Figure 6 (bottom-right), we choose n = 4 and α = 3.

4. Direction for Further Research

We observe the behavior of complex roots of the q-Euler polynomials , using numerical investigation. How many roots does have in general? This is an open problem. Prove or disprove: has n distinct solutions, that is, all the zeros are nondegenerate. Find the numbers of complex zeros of . Since n is the degree of the polynomial , the number of real zeros lying on the real plane Im (x) = 0 is then , where denotes complex zeros. See Table 1 for tabulated values of and . We prove that , has Im (x) = 0 reflection symmetry analytic complex functions. If , then , where * denotes complex conjugate (see Figures 1, 2, and 3). The theoretical prediction on the zeros of requires further study. In order to study the q-Euler polynomials , we must understand the structure of the q-Euler polynomials . Therefore, using computer, in a realistic study for the q-Euler polynomials play an important part. The authors have no doubt that investigation along this line will lead to a new approach employing numerical method in the field of research of the q-Euler polynomials to appear in mathematics and physics. For related topics the interested reader is referred to [16].

References

1 Cenkci M., Can M., and Kurt V., q-adic interpolation functions and Kummer-type congruences for q-twisted and q-generalized twisted Euler numbers, Advanced Studies in Contemporary Mathematics. (2004) 9, no. 2, 203–216, 2090123.
Google Scholar
2 Can M., Cenkci M., Kurt V., Simsek Y., and Yilmaz, Twisted Dedekind type sums associated with Barnes′ type multiple Frobenius-Euler l-functions, Advanced Studies in Contemporary Mathematics. (2009) 18, no. 2, 135–160, 2508979.
Google Scholar
3 Bayad A., Modular properties of elliptic Bernoulli and Euler functions, Advanced Studies in Contemporary Mathematics. (2010) 20, no. 3, 389–401, 2676907.
Google Scholar
4 Kim T., An analogue of Bernoulli numbers and their congruences, Reports of the Faculty of Science and Engineering. (1994) 22, no. 2, 21–26, 1257601, ZBL0802.11007.
Google Scholar
5 Kim T., On the q-extension of Euler and Genocchi numbers, Journal of Mathematical Analysis and Applications. (2007) 326, no. 2, 1458–1465, https://doi.org/10.1016/j.jmaa.2006.03.037, 2280996.
10.1016/j.jmaa.2006.03.037
Web of Science® Google Scholar
6 Kim T., q-Volkenborn integration, Russian Journal of Mathematical Physics. (2002) 9, no. 3, 288–299, 1965383, ZBL1092.11045.
Web of Science® Google Scholar
7 Kim T., q-Euler numbers and polynomials associated with p-adic q-integrals, Journal of Nonlinear Mathematical Physics. (2007) 14, no. 1, 15–27, https://doi.org/10.2991/jnmp.2007.14.1.3, 2287831.
10.2991/jnmp.2007.14.1.3
Web of Science® Google Scholar
8 Kim T., [email protected], Choi J., [email protected], Kim Y. H., and [email protected], Ryoo C. S., [email protected], A note on the weighted p-adic q-Euler measure ℤ_p, Advanced Studies in Contemporary Mathematics. (2011) 21, no. 1, 35–40.
Google Scholar
9 Kupershmidt B. A., Reflection symmetries of q-Bernoulli polynomials, Journal of Nonlinear Mathematical Physics. (2005) 12, no. supplement 1, 412–422, https://doi.org/10.2991/jnmp.2005.12.s1.34, 2118876.
10.2991/jnmp.2005.12.s1.34
Web of Science® Google Scholar
10 Kim T., Bayad A., and Kim Y. H., A study on the p-adic q-integral representation on ℤ_p associated with the weighted q-Bernstein and q-Bernoulli polynomials, Journal of Inequalities and Applications. (2011) 2011, 8, 513821, 2765287.
10.1155/2011/513821
Google Scholar
11 Kim T., New approach to q-Euler polynomials of higher order, Russian Journal of Mathematical Physics. (2010) 17, no. 2, 218–225, https://doi.org/10.1134/S1061920810020068, 2660920.
10.1134/S1061920810020068
Web of Science® Google Scholar
12 Kim T., Some identities on the q-Euler polynomials of higher order and q-Stirling numbers by the fermionic p-adic integral on ℤ_p, Russian Journal of Mathematical Physics. (2009) 16, no. 4, 484–491, https://doi.org/10.1134/S1061920809040037, 2587805.
10.1134/S1061920809040037
Web of Science® Google Scholar
13 Kim T., Barnes-type multiple q-zeta functions and q-Euler polynomials, Journal of Physics A. (2010) 43, no. 25, 11, https://doi.org/10.1088/1751-8113/43/25/255201, 2653033, 255201.
10.1088/1751-8113/43/25/255201
Google Scholar
14 Ozden H., Simsek Y., Rim S.-H., and Cangul I. N., A note on p-adic q-Euler measure, Advanced Studies in Contemporary Mathematics. (2007) 14, no. 2, 233–239, 2316989.
Google Scholar
15 Ryoo C. S., On the generalized Barnes type multiple q-Euler polynomials twisted by ramified roots of unity, Proceedings of the Jangjeon Mathematical Society. (2010) 13, no. 2, 255–263, 2676690.
Google Scholar
16 Ryoo C. S. and Kim T., A numerical computation of the structure of the roots of q-Bernoulli polynomials, Journal of Computational and Applied Mathematics. (2008) 214, no. 2, 319–332, https://doi.org/10.1016/j.cam.2007.02.041, 2398335.
10.1016/j.cam.2007.02.041
Web of Science® Google Scholar
17 Simsek Y., Kurt V., and Kim D., New approach to the complete sum of products of the twisted h,q-Bernoulli numbers and polynomials, Journal of Nonlinear Mathematical Physics. (2007) 14, no. 1, 44–56, https://doi.org/10.2991/jnmp.2007.14.1.5, 2287833.
10.2991/jnmp.2007.14.1.5
Web of Science® Google Scholar
18 Simsek Y., Theorems on twisted L-function and twisted Bernoulli numbers, Advanced Studies in Contemporary Mathematics. (2006) 12, 237–246, 2169895.
Google Scholar
19 Rim S.-H., Moon E.-J., Lee S.-J., and Jin J.-H., Multivariate twisted p-adic q-integral on ℤ_p associated with twisted q-Bernoulli polynomials and numbers, Journal of Inequalities and Applications. (2010) 2010, 6, 579509, 2733601.
10.1155/2010/579509
Google Scholar

Citing Literature

All articles

A Note on the q-Euler Numbers and Polynomials with Weak Weight α

Abstract

1. Introduction

2. Basic Properties for q-Euler Numbers and Polynomials with Weak Weight α

3. Distribution and Structure of the Zeros

4. Direction for Further Research

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Note on the q-Euler Numbers and Polynomials with Weak Weight α

Abstract

1. Introduction

2. Basic Properties for q-Euler Numbers and Polynomials with Weak Weight α

3. Distribution and Structure of the Zeros

4. Direction for Further Research

References

Citing Literature

Figures

References

Related

Information