Photoionization Processes of the Single-Ionized Boron
Abstract
The relativistic calculations of the cross-section σ, the angular-distribution parameter β, and spin-polarization parameters {ξ, η, ζ} of photoelectrons using the multiconfiguration relativistic random-phase approximation theory for the photoionization of the B+ ion are presented. Precise energies and widths of all five Rydberg series of doublyexcited states , , , , and are determined. Our predictions are in very close agreement with experiments and are consistent with other calculations.
1. Introduction
Experimental and theoretical studies of photoionization processes are of fundamental importance because they have greatly increased the understanding of the responses of atoms or ions to electromagnetic radiations. In recent years, the development of merged ion-photon beams and third-generation synchrotron radiation facilities provides sufficiently high density of target ions and the required incident photon flux. These high-resolution measurements attributed to rapidly evolving experimental techniques enhanced the ability to study the photoionization of atomic systems along isoelectronic, isonuclear, and isoionic series.
Divalence atomic systems such as the Be-isoelectronic sequence are attractive candidates for the systematic studies of the photoionization processes because of their relatively simple quasi-two-electron structure. In these atomic systems, two loosely bound electrons in the L-shell are well separated from the other two tightly bound K-shell electrons. They are suitable for comprehensive studies of electron-correlation and relativistic effects in photoionization processes. In addition, many works have shown that relativistic effects play an important role in the photoionization of small atoms, such as Be [1–4], Ne [5], and Mg [6–8]. Therefore, it is worthwhile to investigate the interplay between electron-correlation and relativistic effects on the photoionization of atoms or ions with a low nuclear charge.
Considerable theoretical and experimental efforts have been made recently to investigate the photoionization of the B+ ion. Among the theoretical results are the R-matrix calculations of Tully et al. [9, 10], the B-spline-based configuration-interaction approach of Chang and Zhu [11], and the noniterative eigenchannel R-matrix method of Kim and Manson [12].
On the experimental side, the absorption spectrum of B+ has been measured by Esteva [13]. Jannitti et al. [14] investigated the absorption spectrum of B+ for photon energies between 400 and 1700 Å by using two-laser produced plasma. Recently, a good agreement between theory and experiment for the photoionization of the B+ ion was performed by Schippers et al. [15] by using a photon-ion merged-beams arrangement at the advanced light source. They also calculated the photoionization cross section using the semirelativistic Breit-Pauli R-matrix approach.
The multiconfiguration relativistic random-phase approximation theory (MCRRPA) has been successfully applied to photoexcitation [16–29] and photoionization [1, 8, 28, 30–34] of divalence atomic systems. Double-excitation resonances in the photoionization spectrum reveal electron-correlation and relativistic effects and therefore provide a stringent testing ground for the accuracy of theoretical models. In the photon-energy region between (1s22s) 2S1/2 and ionization thresholds of the B+ ion, double-excitation autoionization resonances are the most prominent feature in its photoionization spectrum. These double-excitation resonances may be classified into five Rydberg series: , , , , and .
Most of the earlier nonrelativistic studies have focused only on two singlet Rydberg series and . In the nonrelativistic calculation, the cross section should be similar to the MCRRPA result but without the extremely sharp resonance structures of triplet resonances , , and . These resonances are the result of relativistic effects, without which they are completely forbidden. Because of the incorporation of relativity in the MCRRPA calculation, the double-excitation resonances in the photoionization spectrum belonging to all five Rydberg series of the B+ ion are built-in from the outset.
The main concerns of most photoionization researches are with the corss section. Nevertheless, a complete macroscopic analysis of photoionization processes also requires knowledge of the angular distribution and spin polarization of photoelectrons. In the nonrelativistic limit, these extra parameters are all constant. In this work, we continue our previous investigation of the photoionization processes of the B+ ion by using the MCRRPA theory [35]. The cross section, angular distribution, and spin polarization of photoelectrons including all five Rydberg series of low-lying doubly excited states , , , , and are studied in detail, accounting for all relativistic excitation channels. In Section 2, we review our method briefly. Results are presented in Section 3, and the conclusion is made in Section 4.
2. MCRRPA Theory
- (i)
Photoionization channels:
- (a)
,
- (b)
.
- (a)
- (ii)
Photoexcitation channels:
- (c)
, n ≥ 3,
- (d)
,
- (e)
,
- (f)
,
- (g)
.
- (c)
The couplings between the photoionization and photoexcitation channels generate five autoionization resonance series in the photoionization spectrum.
We note particularly that for photoionization of an unpolarized B+ ion, only three of the five parameters {σ, β, ξ, η, ζ} are independent, which may be expressed in terms of three independent quantities {|DS|, |DT|, ϕ}.
3. Results and Discussions
In the present work, we investigate the photoionization spectrum of the B+ ion in the region of interest by using the MCRRPA theory. We consider the incident photon with energy between the ionization thresholds (1s22s) 2S1/2 and , where only photoionization channels (a) and (b) are open. The couplings of the two photoionization channels and remaining five photoexcitation channels provide the paths for the doubly excited states to decay through autoionization. As a result, the photoionization cross section in the range is dominated by the five Rydberg series of resonances , , , , and . The comparison of our photoionization cross section with those of selected theory and expreiment is presented in Figure 1. In our calculation, predicted profiles of the autoionization resonances are in very close agreement with experimental measurements.
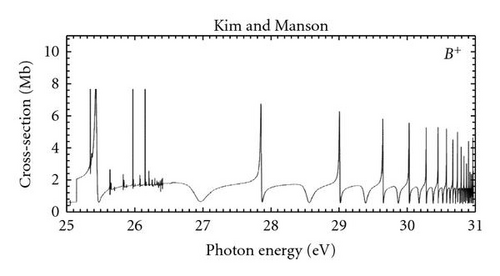
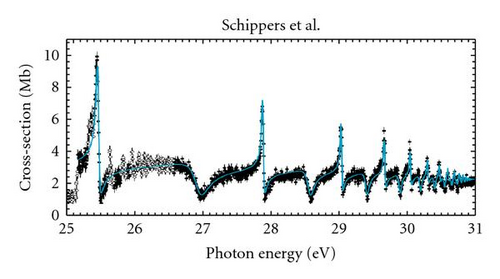
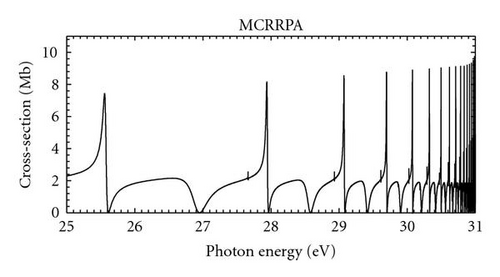
The curve in Figure 1(c) represents the seven-channel MCRRPA calculation which shows all five Rydberg series of resonances obtained from the couplings of the two photoionization channels with all five photoexcitation channels. The photoionization cross section is characterized by a nonresonant background of about 2 Mb with resonance structures. Because the photoionization continuum and the double-excitation series and all arise from the n = 2 atomic complex and with the same total spin and orbital angular-momenta, the couplings between them are strong so that the characteristics of the cross section are completely dominated by double-excitation resonances and . The Rydberg series appear as broad autoionizing resonances in the photoionization cross-section while the narrower Rydberg series is sandwiched amid the Rydberg series . The strong couplings between doubly excited states and the continuum give rise to broad resonances; however, the narrower resonances are due to the weaker couplings between states and continuum . Broad resonances indicate short lifetimes of the corresponding doubly excited states while the narrow profiles reveal long lifetimes.
Photoionization cross sections σ and corresponding phase shifts δ of the first five resonances are shown in Figure 2 as a demonstration, where σm indicates the cross-section minimum, Er the resonance energy, and Γr the width of the resonance. The phase shift δ increases π in the vicinity of each resonance; a slower variation in the phase shift indicates a broader resonance, that is, a shorter lifetime. Phase-shift variations allow us to identify theoretically precise positions and widths of pseudobound states. The precise positions Er and widths Γr of double-excitation resonances belonging to five Rydberg series for the MCRRPA calculation are derived from phase-shift variations.
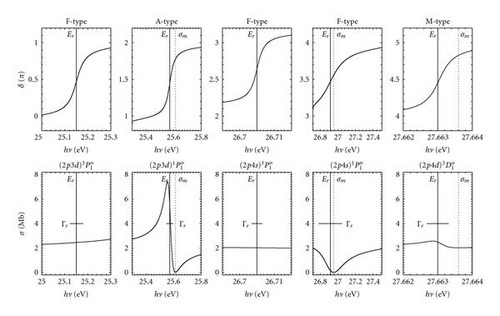
The allowed double-excited states and are well separated for a parametric fit to be made in the way suggested by Dubau and Seaton [41], within the framework of the quantum defect theory. In Tables 1 and 2, we present effective quantum numbers ν, quantum defects μ, resonance energies Er, and the Beutler-Fano parameter q [42], which describe the resonance profiles. Table 3 present the resonance widths Γr of allowed doubly excited states and of our MCRRPA calculations and other currently available data. Our present calculations are compared with theoretical results of Tully et al. [9, 10], Chang and Zhu [11], and Kim and Manson [12]. Experimental results of Esteva [13], Jannitti et al. [14], and Schippers et al. [15] are also listed for comparison. The quantum defects μ of the series are positive and those of the series are negative and small. It shows a fair agreement of our predicted positions Er and widths Γr, as well as parameters ν, μ, and q of the series and with those of previous results. In Tables 4, 5, and 6, we present the effective quantum numbers ν, quantum defects μ, resonance energies Er, and resonance widths Γr of doubly excited states , , and of B+ from the MCRRPA calculation.
| ν | μ | Er (eV) | q | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| State | Present | [11] | [12] | Present | Present | [14] | [9] | [12] | [15] | Present | [15] |
| 3.58398749 | 3.6014 | 3.6036 | 0.41590601 | 26.9137 | 26.91 | 26.96 | 26.9405 | 26.923 | −0.30281 | −0.46(3) | |
| 4.58645218 | 4.6003 | 4.5994 | 0.41344131 | 28.5634 | 28.58 | 28.59 | 28.5568 | 28.580 | −0.29740 | −0.22(3) | |
| 5.58917807 | 5.5995 | 5.5975 | 0.41071543 | 29.4084 | 29.44 | 29.42 | 29.3924 | 29.420 | −0.29246 | −0.16(5) | |
| 6.59248356 | 6.5994 | 6.5966 | 0.40740993 | 29.8983 | 29.8787 | 29.895 | −0.29025 | −0.34(7) | |||
| 7.59693592 | 7.5994 | 7.5955 | 0.40295757 | 30.2075 | 30.1861 | 30.205 | −0.28880 | −0.35(9) | |||
| 8.60267519 | 8.5952 | 0.39721830 | 30.4151 | 30.3927 | 30.409 | −0.29036 | −0.4(2) | ||||
| 9.61018655 | 9.5944 | 0.38970694 | 30.5612 | 30.5382 | 30.562 | −0.29370 | −0.2(3) | ||||
| 10.61981847 | 10.5953 | 0.38007502 | 30.6680 | 30.6444 | −0.29820 | ||||||
| 11.63196241 | 11.5927 | 0.36793108 | 30.7483 | 30.7244 | −0.30278 | ||||||
| 12.64717198 | 0.35272151 | 30.8103 | −0.30577 | ||||||||
| 13.66560285 | 0.33429064 | 30.8591 | −0.30698 | ||||||||
| 14.68741014 | 0.31248335 | 30.8982 | −0.30498 | ||||||||
| 15.71318796 | 0.28670553 | 30.9301 | −0.30013 | ||||||||
| 16.74273514 | 0.25715835 | 30.9564 | −0.29126 | ||||||||
| 17.77644603 | 0.22344747 | 30.9783 | −0.27782 | ||||||||
| 18.81451302 | 0.18538047 | 30.9968 | −0.25592 | ||||||||
| 19.85735657 | 0.14253693 | 31.0125 | −0.21239 | ||||||||
| ν | μ | Er (eV) | q | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| State | Present | [11] | [12] | Present | Present | [14] | [9] | [12] | [13] | [15] | Present | [15] |
| 3.12372213 | 3.0948 | 3.0891 | −0.12375763 | 25.5731 | 25.43 | 25.47 | 25.4262 | 25.44 | 25.458(1) | −1.58033 | −2.21(8) | |
| 4.12062029 | 4.0883 | 4.0862 | −0.12065579 | 27.9453 | 27.91 | 27.90 | 27.8610 | 27.90 | 27.889(1) | −1.74855 | −1.86(6) | |
| 5.12036077 | 5.0849 | 5.0753 | −0.12039627 | 29.0747 | 29.06 | 29.05 | 29.0166 | 29.04 | 29.041(1) | −1.83648 | −2.0(1) | |
| 6.12180122 | 6.0832 | 6.0720 | −0.12183672 | 29.6983 | 29.70 | 29.68 | 29.6533 | 29.676(1) | −1.88850 | −2.3(2) | ||
| 7.12467028 | 7.0824 | 7.0708 | −0.12470578 | 30.0784 | 30.0408 | 30.064(2) | −1.92160 | −1.9(2) | ||||
| 8.12901572 | 8.0689 | −0.12905122 | 30.3269 | 30.2935 | 30.320(2) | −1.94378 | −1.4(3) | |||||
| 9.13497539 | 9.0681 | −0.13501089 | 30.4983 | 30.4676 | 30.490(4) | −1.96123 | −1.8(7) | |||||
| 10.14277810 | 10.0668 | −0.14281360 | 30.6215 | 30.5924 | 30.61(1) | −1.97372 | −2(3) | |||||
| 11.15267006 | 11.0667 | −0.15270556 | 30.7130 | 30.6850 | −1.98510 | |||||||
| 12.16500247 | 12.0664 | −0.16503797 | 30.7828 | 30.7556 | −2.00091 | |||||||
| 13.18004710 | −0.18008260 | 30.8372 | −2.00782 | |||||||||
| 14.19816003 | −0.19819553 | 30.8805 | −2.02644 | |||||||||
| 15.21966360 | −0.21969910 | 30.9156 | −2.04491 | |||||||||
| 16.24485313 | −0.24488863 | 30.9443 | −2.05882 | |||||||||
| 17.27398677 | −0.27402227 | 30.9681 | −2.08818 | |||||||||
| 18.30732396 | −0.30735946 | 30.9881 | −2.13133 | |||||||||
| 19.34503370 | −0.34506920 | 31.0051 | −2.17179 | |||||||||
| 20.38717585 | −0.38721135 | 31.0196 | −2.21833 | |||||||||
| State | Present | [9] | [12] | [15] | State | Present | [9] | [12] | [15] |
|---|---|---|---|---|---|---|---|---|---|
| 5.1662 [−2] | 0.0338 | 0.0312 | 0.034(2) | ||||||
| 2.6625 [−1] | 0.241 | 0.2453 | 0.22(1) | 2.2066 [−2] | 0.0178 | 0.0141 | 0.016(2) | ||
| 1.1884 [−1] | 0.110 | 0.1153 | 0.106(7) | 1.1369 [−2] | 0.0101 | 0.0095 | 0.010(3) | ||
| 6.3431 [−2] | 0.059 | 0.0635 | 0.048(6) | 6.6047 [−3] | 0.0061 | 0.0064 | 0.008(3) | ||
| 3.7884 [−2] | 0.0384 | 0.029(7) | 4.1691 [−3] | 0.0044 | 0.008(4) | ||||
| 2.4421 [−2] | 0.0249 | 0.020(6) | 2.7948 [−3] | 0.0031 | 0.001(6) | ||||
| 1.6628 [−2] | 0.0171 | 0.04(1) | 1.9600 [−3] | 0.0023 | 0.005(8) | ||||
| 1.1792 [−2] | 0.0122 | 0.02(2) | 1.4224 [−3] | 0.0017 | |||||
| 8.6287 [−3] | 0.0090 | 1.0597 [−3] | 0.0013 | ||||||
| 6.4650 [−3] | 0.0069 | 8.0546 [−4] | 0.0011 | ||||||
| 4.9271 [−3] | 6.2136 [−4] | ||||||||
| 3.8080 [−3] | 4.8446 [−4] | ||||||||
| 2.9780 [−3] | 3.8033 [−4] | ||||||||
| 2.3560 [−3] | 2.9932 [−4] | ||||||||
| 1.8842 [−3] | 2.3491 [−4] | ||||||||
| 1.5206 [−3] | 1.8234 [−4] | ||||||||
| 1.2342 [−3] | 1.3760 [−4] | ||||||||
| 9.9928 [−4] | 9.6857 [−5] |
| State | ν | μ | Er(eV) | Γr(eV) |
|---|---|---|---|---|
| 3.49886452 | 0.50102897 | 26.7050 | 3.1666 [−3] | |
| 4.50647877 | 0.49341472 | 28.4707 | 2.2077 [−3] | |
| 5.51095458 | 0.48893891 | 29.3586 | 1.4766 [−3] | |
| 6.51427249 | 0.48562100 | 29.8680 | 1.0529 [−3] | |
| 7.51718124 | 0.48271226 | 30.1874 | 8.2485 [−4] | |
| 8.51997402 | 0.47991948 | 30.4008 | 7.1353 [−4] | |
| 9.52274311 | 0.47715038 | 30.5504 | 6.7072 [−4] | |
| 10.52545978 | 0.47443371 | 30.6593 | 6.6420 [−4] | |
| 11.52799675 | 0.47189674 | 30.7410 | 6.7133 [−4] | |
| 12.53029879 | 0.46959470 | 30.8039 | 6.7618 [−4] | |
| 13.53230180 | 0.46759169 | 30.8533 | 6.7006 [−4] | |
| 14.53396478 | 0.46592871 | 30.8929 | 6.5118 [−4] | |
| 15.53535434 | 0.46453915 | 30.9250 | 6.2169 [−4] | |
| 16.53651255 | 0.46338095 | 30.9515 | 5.8588 [−4] | |
| 17.53755426 | 0.46233923 | 30.9736 | 5.4804 [−4] | |
| 18.53863090 | 0.46126259 | 30.9922 | 5.1127 [−4] | |
| 19.53981972 | 0.46007377 | 31.0080 | 4.7834 [−4] |
| State | ν | μ | Er(eV) | Γr(eV) |
|---|---|---|---|---|
| 3.01169305 | −0.01174631 | 25.1505 | 5.7916 [−2] | |
| 4.00040202 | −0.00045527 | 27.7498 | 2.6153 [−2] | |
| 4.99656346 | 0.00338328 | 28.9706 | 1.3576 [−2] | |
| 5.99639543 | 0.00355132 | 29.6370 | 7.8561 [−3] | |
| 6.99873582 | 0.00121093 | 30.0394 | 4.9165 [−3] | |
| 8.00324320 | −0.00329645 | 30.3008 | 3.2572 [−3] | |
| 9.00993439 | −0.00998764 | 30.4801 | 2.2500 [−3] | |
| 10.01894075 | −0.01899400 | 30.6083 | 1.6047 [−3] | |
| 11.03048438 | −0.03053763 | 30.7032 | 1.1743 [−3] | |
| 12.04477723 | −0.04483048 | 30.7754 | 8.7870 [−4] | |
| 13.06207788 | −0.06213113 | 30.8315 | 6.7093 [−4] | |
| 14.08255995 | −0.08261320 | 30.8761 | 5.2178 [−4] | |
| 15.10650188 | −0.10655513 | 30.9120 | 4.1276 [−4] | |
| 16.13412774 | −0.13418099 | 30.9414 | 3.3160 [−4] | |
| 17.16567630 | −0.16572955 | 30.9658 | 2.7007 [−4] | |
| 18.20134937 | −0.20140262 | 30.9862 | 2.2275 [−4] | |
| 19.24138849 | −0.24144174 | 31.0035 | 1.8576 [−4] | |
| 20.28601671 | −0.28606996 | 31.0183 | 1.5654 [−4] |
| State | ν | μ | Er(eV) | Γr(eV) |
|---|---|---|---|---|
| 3.95032905 | 0.04961770 | 27.6630 | 6.4052 [−4] | |
| 4.95151535 | 0.04843140 | 28.9308 | 2.1109 [−4] | |
| 5.95309632 | 0.04685043 | 29.6149 | 1.1973 [−4] | |
| 6.95516111 | 0.04478564 | 30.0255 | 9.9782 [−5] | |
| 7.95771747 | 0.04222927 | 30.2911 | 1.0149 [−4] | |
| 8.96071925 | 0.03922750 | 30.4727 | 1.1066 [−4] | |
| 9.96407888 | 0.03586787 | 30.6023 | 1.2114 [−4] | |
| 10.96768768 | 0.03225907 | 30.6981 | 1.2967 [−4] | |
| 11.97143623 | 0.02851052 | 30.7708 | 1.3501 [−4] | |
| 12.97522199 | 0.02472476 | 30.8272 | 1.3728 [−4] | |
| 13.97894846 | 0.02099829 | 30.8720 | 1.3730 [−4] | |
| 14.98255856 | 0.01738819 | 30.9081 | 1.3584 [−4] | |
| 15.98600505 | 0.01394170 | 30.9375 | 1.3417 [−4] | |
| 16.98928921 | 0.01065753 | 30.9620 | 1.3295 [−4] | |
| 17.99240347 | 0.00754328 | 30.9824 | 1.3334 [−4] | |
| 18.99541257 | 0.00453418 | 30.9997 | 1.3705 [−4] | |
| 19.99837621 | 0.00157054 | 31.0144 | 1.4764 [−4] |
Physically, the coupling strength between the bound and continuum components of the wave function of a doubly excited state is measured by the resonant width Γr, which also determines the nonradiative decay rate of an autoionization state. Because the orbital symmetries of the photoionization channels and are of P-type, the coupling of resonances with these photoionization channels are weaker such that their widths are much narrower. There are, however, some discrepancies between theoretical results for resonance widths. Our MCRRPA calculation, which deals with all five Rydberg series, includes relativistic and correlation in an ab initio manner and treats the initial and final states in a balanced fashion; therefore, it should in principle provide reliable lifetimes within the model itself.
In comparison with our previous MCRRPA results for neutral Be [3], the stronger nuclear field of the B+ ion moves a number of the near-threshold resonances below the ionization threshold of the B+ ion and thereby alters the behavior of the cross section considerably. In addition, the couplings among the resonances are greater for the B+ ion than the Be atom, because the energy gap between (1s22s) 2S1/2 and thresholds of the B+ ion are smaller than that of the Be atom. This compression leads to the implication that couplings of resonances will become stronger for the photoionization of higher members of the Be isoelectronic sequence.
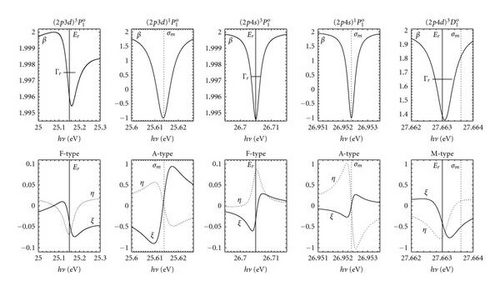
The angular-distribution and spin-polarization parameters {β, ξ, η, ζ} for photoelectrons by seven-channel MCRRPA calculations in the double-excitation resonance region are given in Figure 3. These parameters deviate from their nonrelativistic limits due to relativistic effects which permit couplings with forbidden channels. In the nonrelativistic limit, the final state should be of the type and DT = 0 such that β = 2 and ξ = η = ζ = 0. All these parameters, which have varied sharply at locations of resonances, display primarily three classes of characteristic behaviors, A-type for allowed resonances and , F-type for forbidden resonances and , and M-type for forbidden resonances , which resemble a mixture of A-type and F-type.
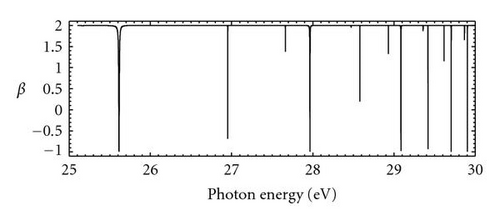
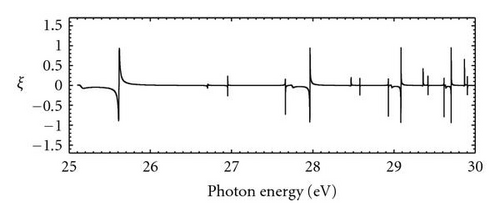
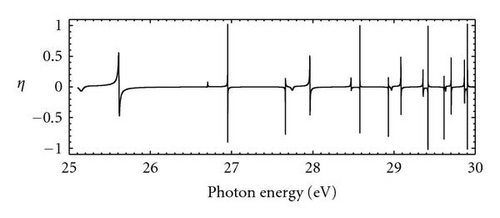
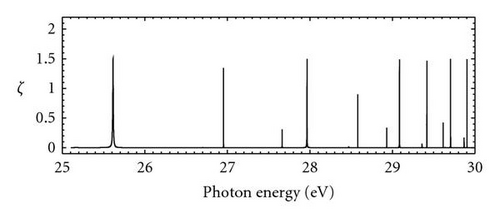
The parameters {β, ξ, η} for A-type resonances and , F-type resonances for and , and M-type resonance for (2p4d) around the resonances are given in Figure 4 as a demonstration. Around the A-type resonances, we observe marked departures of β from its background value 2, and β reaches its minimum −1 at the resonance minimum σm. The parameters ξ and η change sign through the resonance minimum and vary reciprocally to the energy departure from the resonance minimum. Furthermore, it is worth noting that although the cross section in (2) is independent of the relative phase, the resonance minimum reveal the position where the relative phase goes through π rapidly. In the neighborhood of F-type resonances, the variations of photoionization parameters are much smaller and less symmetric about the resonance energy Er, compared to those of the A-type resonances. It is also reasonable that the variations of β and ζ reach their extrema near the resonance energy Er for resonances and , and the half-width of the variations is also approximately the resonance width Γr. The resonance structures of photoionization parameters for the M-type resonance take place at the resonance energy Er, which resembles that of F-type whereas a very deep cross section minimum also occurs near the resonance structure, similar to that of A-type. These near-resonance characteristics of the interesting detuning for photoionization parameters of photoelectrons from the Single-Ionized boron share the similar features of those from the neutral beryllium [3] and may be understood by considering the behaviors of photoionization amplitudes DS, DT, and the relative phase ϕ.
4. Conclusion
In summary, notable features in the processes of the simultaneous excitation of two valence electrons of the B+ ion by a single photon are the double-excitation resonances in the photoionization spectrum, angular distributions, and spin polarizations of photoelectrons. Resonance energies Er and widths Γr of all five Rydberg series, , , , , and , of low-lying doubly excited states of the B+ ion are studied in detail including electron-correlation and relativistic effects. The angular-distribution and spin-polarization parameters {β, ξ, η, ζ}, which have pronounced variations in the vicinity of each double-excitation resonance, display primarily three classes of characteristic behaviors, namely, A-type for allowed resonances and , F-type for forbidden resonances and , and M-type for forbidden resonances with large spin-orbit coupling effects.
The positions of resonance energies Er are in general agreement with previous experiments and theoretical calculations. The B+ ion with a low nuclear charge behaves more or less nonrelativistically, only two of the five resonance series dominate the photoionization cross section. Therefore, experimental data are only available for the energies Er and widths Γr of two singlet Rydberg series and and do not provide much information on the triplet Rydberg series. Consequently, the MCRRPA results for resonance structures in general agree well with previous nonrelativistic theoretical and experimental results, apart from the extremely sharp resonances for triplet Rydberg series. However, it is possible to experimentally obtain both energies and widths of the triplet Rydberg series , , and by measuring the photoelectron angular-distribution parameter β. Nevertheless, for this purpose, spin-polarization measurements of photoelectrons could always be independent verifications. Experimental studies on angular distribution of photoelectrons are suggested to obtain information on widths of some states, which cannot be obtained from total cross section measurements.
Acknowledgment
This paper was supported in part by the National Science Council of Taiwan under Grant no. NSC99-2112-M-001-023.




