A Statistical Approach to the Forward Kinematics Nonlinearity Analysis of Gough-Stewart Mechanism

1. Introduction

The Gough-Stewart platform mechanism (GSPM), introduced by Gough and Whitehall [1] and Stewart [2], was originally used as a universal six degree of freedom (6-DOF) mechanism in a tire test machine and a flight simulator. Later on, the mechanism found various applications in many industries like aviation, entertainment, health, surgery, and most recently machine tools. The Stewart platform is a six-degree of freedom parallel mechanism which most commonly comprises a moving platform (referred to as upper platform here) and a fixed platform (referred to as lower platform), six pods, six spherical joints, and six universal joints as shown in Figure 1.

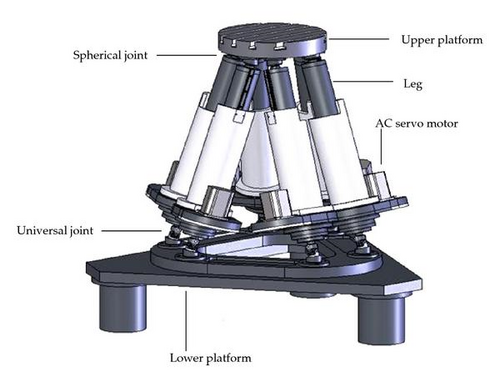
Determination of the lengths of pods and the first and second rate of change in these lengths forms basis of the inverse kinematics analysis of the mechanism. This is done by using the position and orientation, translational and angular velocities, and translational and angular accelerations of the upper platform.

The kinematic chain of the mechanism is illustrated in Figure 2. The ith pod is represented by vector L_i in global coordinate system, connecting the nominal position of the ith universal joint to the nominal position of the ith spherical joint. The nominal positions of the ith spherical and universal joints in global coordinate system are defined by vectors S_i and U_i, respectively.

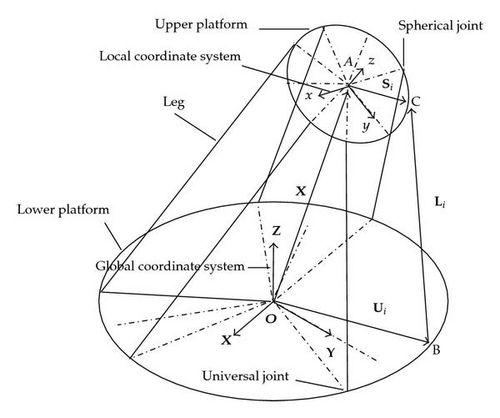
The inverse kinematics problem of the mechanism is fairly simple as discussed exhaustively by Harib and Srinivasan [3], Karimi et al. [4], and Karimi and Nategh [5]. On the contrary, the problem of the forward kinematics is not straightforward. Forward kinematics analysis is concerned with the problem of finding the position/orientation of the upper platform when the lengths of pods are available.

Various methods have already been applied to solve the forward displacement problem of the general Stewart mechanism. Raghavan [6] numerically proved that there are at most 40 possible solutions in the complex domain. Zhang and Song [7] presented closed-form solution to this problem, but without achieving rigorous solutions. Husty [8] produced a 40th-degree univariate polynomial by finding the greatest common divisor of the intermediate polynomials of degree 320. Innocenti [9] obtained a solution from the two 56th-degree univariate equations that are obtained from respective 45   ×   45 matrices. Wampler conducted the forward kinematic analysis of the mechanism using Soma coordinates [10]. Dhingra et al. [11] used the Gröbner-Sylvester hybrid method to obtain a 40th-degree polynomial from the 68   ×   68 Sylvester’s matrix formed by 68 equations of calculated Gröbner basis. Lee and Shim [12] developed an elimination method to derive directly a univariate polynomial of degree 40 from a 28   ×   28 matrix. Later on, they improved the dialytic elimination algorithm [13], with which the size of the Sylvester’s matrix leading to a 40th-degree univariate equation has been reduced to 15 × 15. Huang et al. presented a concise algebraic elimination algorithm to solve the closed-form forward kinematics of the Stewart platform. Based on the presented algebraic method, the forward kinematics problem was reduced to solve a univariate polynomial equation of degree at most 14. The 14th degree univariate polynomial is derived from the determinant of the 15   ×   15 Sylvester’s matrix, which is relatively small in size, without factoring out or deriving the greatest common divisor [14]. Gan et al. presented an algorithm to directly obtain a 40th degree univariate equation from a constructed 13   ×   13 Sylvester’s matrix without factoring out or deriving the greatest common divisor [15]. Hui et al. presented a multivariate polynomial equations set with respect to the moving platform’s position and orientation parameters [16].

Although it is known that at most 40 possible solutions exist for the forward kinematic problem of a general GSPM, only one solution corresponds to the actual pose of a physical machine [3]. Two most common approaches to find directly the actual solution are (i) to use an iterative numerical procedure or (ii) to use extra sensors. Harib employed a numerical iterative technique, based on the Newton-Raphson method [3]. Bonev and Ryu presented a method to solve direct kinematics problem of a general GSPM using three linear extra sensors [17].

Both the inverse and forward kinematics of GSPM exhibit nonlinear behavior. In the inverse kinematics the pods’ lengths do not change linearly with a linear path travelled by the upper platform. In the forward kinematics, when pods are actuated linearly the upper platform moves along a nonlinear path. This makes the path control and interpolation functions in Stewart-based machine tools become more complex than in conventional machine tools. Zheng et al. [18] investigated path control for a novel 5-DOF parallel machine tool. They demonstrated the nonlinearity of both inverse and forward kinematics of the parallel machine tool. Based on the error introduced by the kinematic nonlinearity of the mechanism, they proposed a novel interpolation algorithm, however they did not elaborate the nonlinearity of the mechanism. Beale made the first serious attempt to measure nonlinearity. He proposed four measures of nonlinearity [19]. This problem has been tackled in several research works. Guttman and Meeter showed that Beale’s measures tend to predict that a model will behave linearly even when considerable nonlinearity is present [20]. Box presented a formula for estimating the bias in the LS estimators [21]. Using simulation studies, Gillis and Ratkowsky [22] found that this formula not only predicted bias to the correct order of magnitude in yield-density models, but also gave a good indication of the extent of nonlinear behavior of the model. Bates and Watts developed new measures of nonlinearity based on the geometric concept of curvature [23]. They used the maximum relative intrinsic and parameter-effects curvatures of the solution locus for estimating the extent of nonlinearity. They showed that the projections of the straight and equispaced parametric lines in the parameter space onto the plane tangent to the solution locus are, in general, neither straight, nor equispaced. They established a relationship between their measures of nonlinearity and those of Beale and Box’s bias expressions. They explained that since Beale’s measures yield the average nonlinearity, they tend to underestimate the true nonlinearity. Bates and Watts’s measures of nonlinearity have found various applications in studying nonlinearities.

To the extent that the authors of the present paper are aware, little attention has been paid to the nonlinearity analysis of GSPM. This is especially important for the hexapod machine tools where nonlinearity of the mechanism considerably adds to the interpolation algorithms requiring an insightful analysis. The problem of path control in parallel mechanisms has recently been tackled in some studies, for example [20, 24]. As a continuation of their studies on the hexapod machine tools, the authors have investigated the nonlinearity of the GSPM mechanism employing the Bates and Watts measures of nonlinearity.

2. Kinematics of GSPM

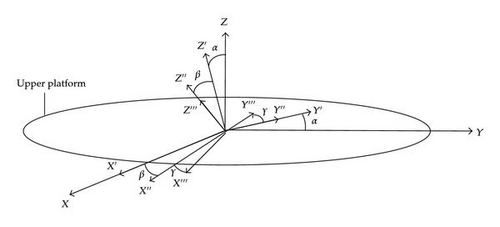
As illustrated in Figure 3, xyz coordinate system is rotated around x-axis by the angle of α, thus obtained x^′y^′z^′. The latter coordinate system is rotated around y^′ by the angle of β to produce x^′′y^′′z^′′. The rotation of x^′′y^′′z^′′ around z^′′ by the angle of γ produces the x^′′′y^′′′z^′′′ coordinate system.

3. Kinematics Nonlinearity

3.2. Nonlinearity of Forward Kinematics

The nonlinearity of forward kinematics is not however as straightforwardly clear. The Bates and Watts measures of nonlinearity are used to study the nonlinearity of the forward kinematics in this section.

Bates and Watts introduced the concept of relative curvature and illustrated that the relative curvature can be decomposed into intrinsic curvature and parameter-effects curvature [23]. Seber and Wild showed that since their measures are scale free, they can be used for different scales of data and parameters [25]. Their methodology is suitable for the consideration of the nonlinearity of regression models in the vicinity of a point on expectation surface, thus validating the linear approximation of the model. To test the linear approximation validity, they suggested to compare both the intrinsic and parameter-effects curvatures to $$ in the 100(1 − a)% confidence region where a is the statistical significance level and p and n − p are the degrees of freedom of numerator and denominator in the F distribution table.

The methodology proposed by Bates and Watts applies well to the nonlinearity analysis of the forward kinematics of GSPM since forward kinematics maps a linear relation in parameter space (known here as joints space, l ∈ τ, a subspace of ℜ⁶) into a nonlinear relation in solution space (known here as upper platform space, P ∈ η, a subspace of ℜ⁶). Although no model is present for the forward kinematics of GSPM, it will be shown that its first and second derivatives can be obtained by using the forward kinematics relations.

The forward kinematic relation is mathematically represented as follows:

$$ ()

where $$ is the length vector, and $$. It is assumed that P is well apart from the singular points and, therefore, f is continuous and twice differentiable in the vicinity of l. It is worthy of mention that the singularity analysis of GSPM has attracted the attention of many researchers over decades. There is a finite number of singular points in the workspace of the mechanism where J_v is irreversible and J_I does not exist so the kinematics does not produce a nontrivial solution. In that case, f is neither continuous nor differentiable in a singular point. The function f can be approximated in the vicinity of any set of pod lengths designated by $$ using the first two terms of the Taylor series, as follows:

$$ ()

where δ^T is the transpose of δ and

$$ ()

The kinematics relations discussed earlier are used to derive $$ and $$. Differentiation (3.3) with respect to time gives

$$ ()

Comparing (3.6) with (2.8) reveals that

$$ ()

where $$ is an element of $$ located in the ith row and jth column of matrix $$. $$ can be calculated at any point from (2.10). Now consider a linear relationship in τ (defined as joints space, l ∈ τ, a subspace of ℜ⁶), as follows:

$$ ()

where

$$ ()

Mapping l onto the expectation surface gives a curve called lifted line as follows [25]:

$$ ()

Bates and Watts [26] considered reparametrizing the model and then rotating the axes of the sample space using an orthogonal matrix obtained by the QR decomposition of matrix $$. This way, they introduced the formulation of the components of curvature. They further suggested an algorithm to maximize the curvature and evaluate the nonlinearity by comparing it with the curvature of the so-called standard sphere [25]. Their algorithm is presented in the appendix.

The maximum curvature of the solution locus in a GSPM is dependent on the position and orientation of the upper platform. It is noteworthy that both $$ and $$ are calculated from Jacobian and its derivative, both of which are functions of position and orientation of the upper platform.

In order to investigate the nonlinearity of the mechanism throughout its workspace, different regions in the solution locus are considered. Region is defined as the linear approximation of the lifted line. The difference between a point on the lifted line and that of the region produces the so-called kinematics error which roots in nonlinear behavior of the forward kinematics of GSPM. Regions are different in the position/orientation of the upper platform, together with their sizes and directions. A typical region can be embodied by position/orientation vector of the upper platform at the beginning, designated by P_s, its length designated by ζ, and its direction as shown in Figure 4. For the sake of simplicity the upper platform is assumed to have the same orientation as P_s all along the region.

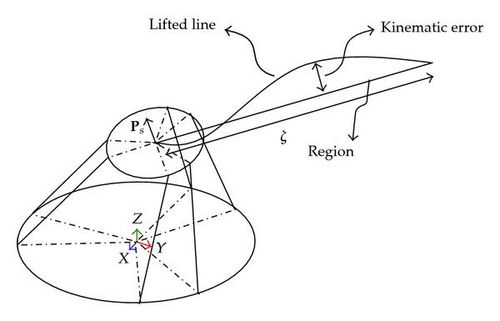
To study the effect of P_s and ζ on the curvature, different levels are chosen for them as is presented in Table 1. For the sake of simplicity, the position and orientation of the upper platform, both of which are included in P_s, are separated and designated by X and O, respectively.

Table 1. Levels of P_s and ζ.

Levels	X  (mm)	O (degree)	ζ (mm)
Level 1	$$	$$	0.05
Level 2	$$	$$	0.08
Level 3	$$	$$	0.1
Level 4	$$	$$	0.5
Level 5	$$	$$	1
Level 6	$$	$$	10
Level 7	$$	$$	50
Level 8	$$	$$	100

The maximum curvature is obtained for any permutation of X, O, and ζ levels as illustrated Figure 5.

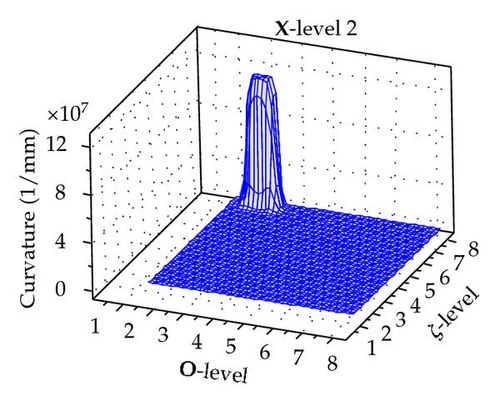
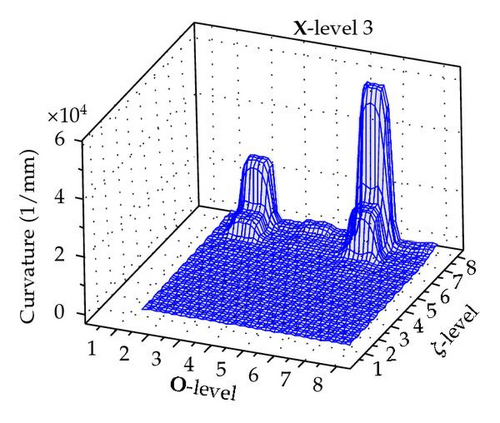
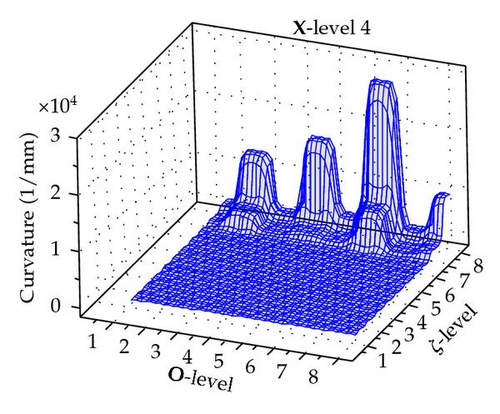
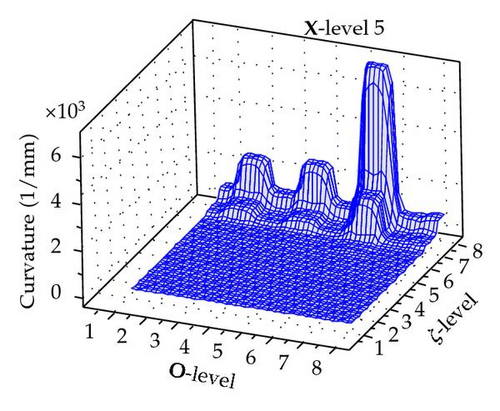
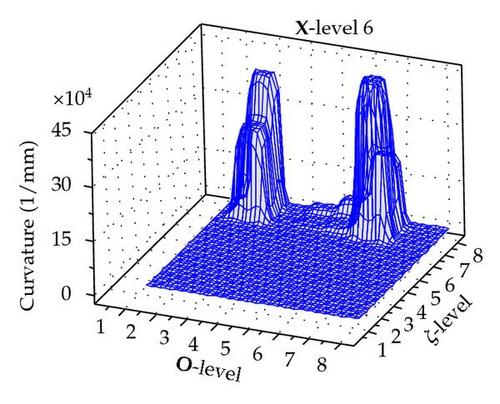
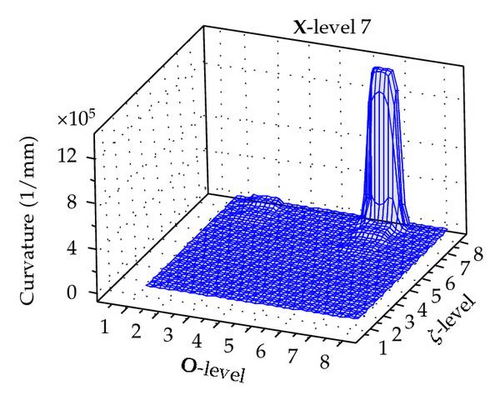
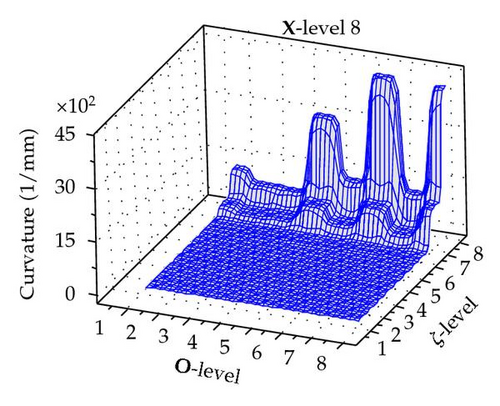
It is apparent that ζ has the greatest impact on the curvature. As it increases the curvature also increases. However there is a clear interaction between the position, orientation, and ζ.

Bates and Watts suggested comparing the maximum parameters-effect curvature with the curvature of 100(1 − a)% confidence region obtained by $$. Here the data in Figure 5 are determined for p = 6 and n = 20. Therefore,

$$ ()

which suggests that linearity assumption should be rejected at 0.05 level of significance, if the curvature in Figure 5 exceed 0.5923.

To elaborate effects of X, O, and ζ on the curvature, plots of main effect and interaction effects are illustrated in Figure 6. Main effect plot of ζ is shown in Figure 7.

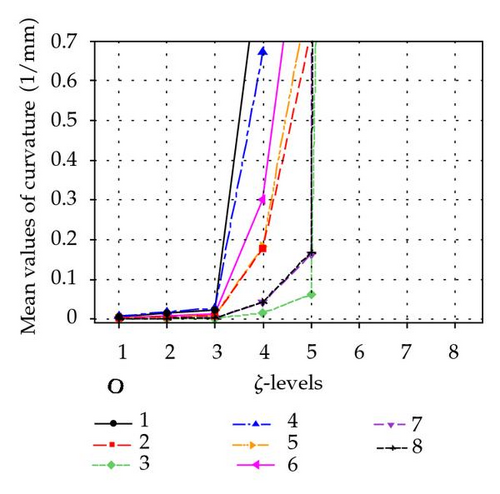
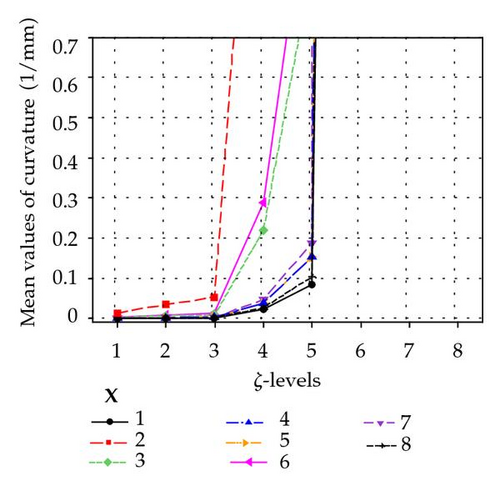
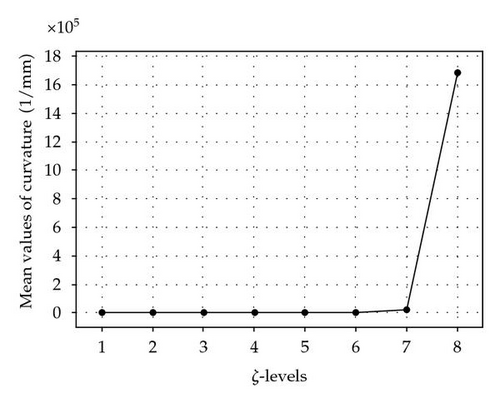
Figure 7 illustrates the mean values of the curvature for levels of ζ, which can be an indicator of the mean effect of ζ on the curvature. As it can be seen from this figure, curvature increases rapidly as the ζ grows, especially for ζ > 1 mm. To check the Bates and Watts measure of nonlinearity, Figure 7 is zoomed around the value of the radius of standard sphere as illustrated in Figure 7.

Figure 8 reveals the fact that for ζ < 0.5 mm, the curvature is less than the radius of standard sphere which correspondingly implies that nonlinearity becomes significant for ζ > 0.5 (mm) the mechanism exhibits nonlinear behavior. Whereas for ζ < 0.5 it can be roughly stated that the mechanism behaves linearly. Interaction plot of location and orientation with ζ is shown as follows.

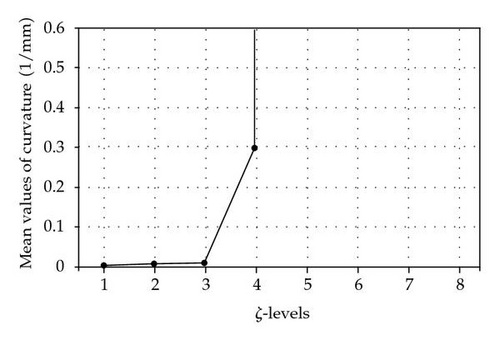
Figure 9 indicates that for ζ < 0.5 mm the nonlinear behavior of the mechanism can be overlooked for all levels of location and orientation based on Bates and Watts measure of nonlinearity.

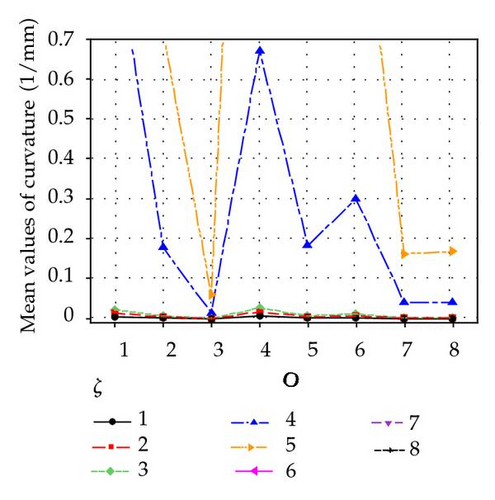
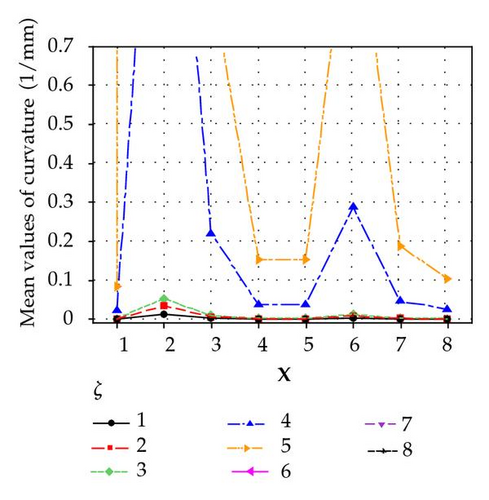
The above discussion leads to the following statement as a rule of thumb that for values of ζ < 0.5 mm the mechanism, shown in Figure 1, exhibits linear behavior.

4. Conclusion

Nonlinearity analysis of GSPM forward and inverse kinematics was presented and considered in this investigation. To quantitatively consider the nonlinearity of the mechanism Bates and Watts measure of nonlinearity was employed. Bates and Watts formulation was developed for the forward kinematics of the mechanism. It was implied that the most significant effect on the nonlinearity of the mechanism is that of the size of the region in the solution locus and it was shown that the nonlinearity of the mechanism is negligible if this size does not exceed 0.5 (mm). Such a conclusion is of significant importance in the interpolation of curves in hexapod machine tool. It was demonstrated that the nonlinear behavior of the mechanism is attributed to the parameter-effect curvature as Bates and Watts classified.