Volume 2011, Issue 1 262316

Research Article

Open Access

Convergence and Divergence of the Solutions of a Neutral Difference Equation

Corresponding Author

G. E. Chatzarakis

[email protected]

Department of Electrical Engineering Educators, School of Pedagogical and Technological Education (ASPETE), N. Heraklion, 14121 Athens, Greece aspete.gr

Search for more papers by this author

G. N. Miliaras,

G. N. Miliaras

Department of Electrical Engineering Educators, School of Pedagogical and Technological Education (ASPETE), N. Heraklion, 14121 Athens, Greece aspete.gr

Search for more papers by this author

G. E. Chatzarakis,

Corresponding Author

G. E. Chatzarakis

[email protected]

Department of Electrical Engineering Educators, School of Pedagogical and Technological Education (ASPETE), N. Heraklion, 14121 Athens, Greece aspete.gr

Search for more papers by this author

G. N. Miliaras,

G. N. Miliaras

Department of Electrical Engineering Educators, School of Pedagogical and Technological Education (ASPETE), N. Heraklion, 14121 Athens, Greece aspete.gr

Search for more papers by this author

First published: 25 October 2011

https://doi.org/10.1155/2011/262316

Citations: 5

Academic Editor: Alexandre Carvalho

Share a link

Email
Wechat
Bluesky

Abstract

We investigate the asymptotic behavior of the solutions of a neutral type difference equation of the form Δ[x(n) + cx(τ(n))] + p(n)x(σ(n)) = 0, where τ(n) is a general retarded argument, σ(n) is a general deviated argument (retarded or advanced), c ∈ ℝ, (p(n)) _n≥0 is a sequence of positive real numbers such that p(n) ≥ p, p ∈ ℝ₊, and Δ denotes the forward difference operator Δx(n) = x(n + 1) − x(n). Also, we examine the asymptotic behavior of the solutions in case they are continuous and differentiable with respect to c.

1. Introduction

Neutral type differential equations are differential equations in which the highest-order derivative of the unknown function appears in the equation both with and without delays (or delays advanced). See Driver [1], Bellman and Cooke [2], and Hale [3] for questions of existence, uniqueness, and continuous dependence.

It is to be noted that, in general, the theory of neutral differential equations presents extra complications, and basic results which are true for delay differential equations may not be true for neutral equations. For example, Snow [4] has shown that, even though the characteristic roots of a neutral differential equation may all have negative real parts, it is still possible for some solutions to be unbounded.

The discrete counterparts of neutral differential equations are called neutral difference equations, and it is a well-known fact that there is a similarity between the qualitative theories of neutral differential equations and neutral difference equations.

Besides its theoretical interest, strong interest in the study of the asymptotic and oscillatory behavior of solutions of neutral type equations (difference or differential) is motivated by the fact that they arise in many areas of applied mathematics, such as circuit theory [5, 6], bifurcation analysis [7], population dynamics [8, 9], stability theory [10], and dynamical behavior of delayed network systems [11]. See, also, Driver [12], Hale [3], Brayton and Willoughby [13], and the references cited therein. This is the reason that during the last few decades these equations are in the main interest of the literature.

In the present paper, we are interested in the first-order neutral type difference equation of the form

()

where (p(n))_n≥0 is a sequence of positive real numbers such that p(n) ≥ p, p ∈ ℝ₊, c ∈ ℝ, (τ(n))_n≥0 is an increasing sequence of integers which satisfies

()

and (σ(n))_n≥0 is an increasing sequence of integers such that

()

Define

()

(Clearly, k is a positive integer.)

By a solution of the neutral type difference equation (E), we mean a sequence of real numbers (x(n)) _n≥−k which satisfies (E) for all n ≥ 0. It is clear that, for each choice of real numbers c_−k, c_−k+1, …, c₋₁,c₀, there exists a unique solution (x(n)) _n≥−k of (E) which satisfies the initial conditions x(−k) = c_−k, x(−k + 1) = c_−k+1, …, x(−1) = c₋₁, x(0) = c₀.

A solution (x(n)) _n≥−k of the neutral type difference equation (E) is called oscillatory if for every positive integer n there exist n₁, n₂ ≥ n such that x(n₁)x(n₂) ≤ 0. In other words, a solution (x(n)) _n≥−k is oscillatory if it is neither eventually positive nor eventually negative. Otherwise, the solution is said to be nonoscillatory.

In the special case where τ(n) = n − a and σ(n) = n − b, a, b ∈ ℕ, (E) takes the form

()

Equation (E) represents a discrete analogue of the neutral type differential equations

()

which, in the special case where τ(t) = t − τ₀ and σ(t) = t − σ₀, τ₀, σ₀ ∈ ℝ₊, takes the form (see e.g., [14, 15])

()

The search for the asymptotic behavior and, especially, for oscillation criteria and stability of neutral type (difference or differential) equations has received a great attention in the last few years. Hence, a large number of related papers have been published. See [4, 9, 10, 14–52] and the references cited therein. Most of these papers are concerning the special case of the delay difference equations (E1) and (E3) where the algebraic characteristic equation gives useful information about oscillation and stability.

The purpose of this paper is to investigate the convergence and divergence of the solutions of (E) in the case of a general delay argument τ(n) and of a general deviated (retarded or advanced) argument σ(n).

2. Some Preliminaries

Assume that (x(n)) _n≥−k is a nonoscillatory solution of (E). Then it is either eventually positive or eventually negative. As (−x(n)) _n≥−k is also a solution of (E), we may (and do) restrict ourselves only to the case where x(n) > 0 for all large n. Let n₁ ≥ −k be an integer such that x(n) > 0 for all n ≥ n₁. Then, there exists n₀ ≥ n₁ such that

()

Set

()

Then, in view of (E) and taking into account the fact that p(n) ≥ p > 0, we have

()

which means that the sequence

is strictly decreasing, regardless of the value of the real constant c.

Throughout this paper, we are going to use the following notation:

()

Let the domain of τ be the set

, where n_* is the smallest natural number that τ is defined with. Then for every n > n_* it is clear that there exists a natural number m(n) such that

()

since (m(n)) is increasing and unbounded function of n.

The following lemma provides some tools which are useful for the main results.

Lemma 2.1. Assume that (x(n)) _n≥−k is a positive solution of (E). Then, one has the following.

(i)
If c ≠ 0 and
()
then
()
(ii)
If
()
then
()
(iii)
If c ≥ −1, then
()
(iv)
If c < −1, then
()

Proof. Summing up (2.3) from n₀ to n, we obtain

()

For the above relation, there are only two possible cases:

()

Assume that (2.15a) holds. Since p(n) ≥ p > 0, we have

()

The last inequality guarantees that

()

and, consequently,

()

Also, (2.15a) guarantess that lim _n→∞z(n) exists as a real number. Now, assume that

()

Since (z(σ(n))) is a subsequence of (z(n)), it is obvious that

()

and, in view of (2.18), we obtain

()

Hence,

()

The proof of part (i) of the lemma is complete.

Assume that (2.15b) holds. Then, by taking limits on both sides of (2.14) we obtain

()

which, in view of the fact that the sequence (z(n)) is strictly decreasing, means that

()

The proof of part (ii) of the lemma is complete.

Assume that −1 ≤ c < 0, and suppose, for the sake of contradiction, that . Then, in view of part (ii), we have z(n) < 0 eventually. Thus,

()

Repeating the above procedure we obtain

()

If −1 < c < 0, clearly, (−c) ^m(n) → 0 since m(n) → ∞ as n → ∞. Since x(n) > 0 for all large n, (2.28) guarantees that

()

This implies that

()

and consequently

, which contradicts our assumption.

If c = −1, by (2.28) we obtain

()

which means that (x(n)) is bounded and therefore (z(n)) is bounded. Hence,

, which contradicts our assumption.

Assume that c ≥ 0 and that . In view of part (ii), (2.10) holds, that is, z(n) < 0 eventually. This contradicts z(n) = x(n) + cx(τ(n)) > 0. Therefore . The proof of part (iii) of the lemma is complete.

In the remainder of this proof, it will be assumed that c < −1.

If (2.15a) holds, that is, , then, in view of part (i), (2.8) is satisfied, that is,

()

If L > 0, then

()

Since (z(n)) is strictly decreasing, we have

()

Repeating this procedure m(n_ℓ) times we have

()

Now, if for this index λ we have x(τ(n_λ)) − (cL/(1 + c)) > 0, then, as n → ∞, x(n) → ∞, which contradicts (2.18). Therefore, there exists an index s such that

()

with

()

Then since lim _n→∞z(n) = cL, for every ɛ > 0 there exists n₂(ɛ) such that

()

where τ(n_s) is satisfying the previous inequality.

Hence,

()

Repeating this procedure m(n_μ) times we have

()

Then, for sufficiently large n the above inequality gives

()

which condradicts x(n) > 0.

If L = 0, then

()

and since (z(n)) is stricly decreasing, it is obvious that z(n) > 0 eventually or

()

In view of (2.6), the last inequality becomes

()

and consequently

()

which contradicts (2.18). Hence, it is clear that

. The proof of part (iv) of the lemma is complete.

The proof of the lemma is complete.

3. Main Results

The asymptotic behavior of the solutions of the neutral type difference equation (E) is described by the following theorem.

Theorem 3.1. For (E) one has the following.

(I)
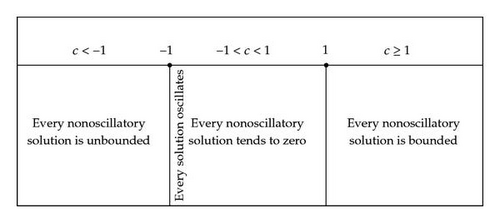
Every nonoscillatory solution is unbounded if c < −1.
(II)
Every solution oscillates if c = −1.
(III)
Every nonoscillatory solution tends to zero if −1 < c < 1.
(IV)
Every nonoscillatory solution is bounded if c ≥ 1.

Furthermore, if any solution of (E) is continuous with respect to c, one has the following.

(V)
Every solution is zero if c ≤ −1.
(VI)
Every solution tends to zero if −1 < c ≤ 1.
(VII)
If, additionally, any solution of (E) has continuous derivatives of any order and convergent Taylor series for every c ∈ ℝ, then the solution is zero.

Proof. Assume that (x(n)) _n≥−k is a nonoscillatory solution of (E). Then it is either eventually positive or eventually negative. As (−x(n)) _n≥−k is also a solution of (E), we may (and do) restrict ourselves only to the case where x(n) > 0 for all large n. Let n₁ ≥ −k be an integer such that x(n) > 0 for all n ≥ n₁. Then, there exists n₀ ≥ n₁ such that

()

which, in view of the previous section, means that the sequence

is strictly decreasing, regardless of the value of the real constant c.

Assume that c < −1. Then, in view of part (iv) of Lemma 2.1, we have , and, consequently, in view of part (ii) of Lemma 2.1, z(n) < 0 eventually. Therefore,

()

Since c < −1, the last relation guarantees that

()

which means that (x(n)) is unbounded. The proof of part (I) of the theorem is complete.

Assume that c = −1. Then, in view of part (iii) of Lemma 2.1, we have , and, therefore, in view of part (i) of Lemma 2.1, we obtain

()

Assume that L > 0. Then there exists a natural number n_λ such that z(n) < 0 for every n ≥ n_λ, and therefore

()

which means that (x(n)) is bounded. Since (x(n)) is bounded, let

()

Then there exists a subsequence (x(θ(n))) of (x(n)) such that

()

Thus,

()

which contradicts (3.7). Therefore, L > 0 is not valid. Hence, L = 0 and consequently lim _n→∞z(n) = 0. Furthermore, taking into account the fact that the sequence (z(n)) is strictly decreasing we conclude that z(n) > 0 or equivalently

()

Since (x(n)) has a lower bound greater than zero, it cannot have any subsequence that tends to zero. Thus, lim _n→∞x(σ(n)) = 0 is not valid, and therefore

which contradicts our previous conclusions. Hence, if c = −1, (x(n)) oscillates. The proof of part (II) of the theorem is complete.

Assume that −1 < c < 0.

Assume that L > 0. Then there exists a natural number n_λ such that z(n) < 0 for every n ≥ n_λ, and therefore

()

which means that (x(n)) tends to zero as n → ∞. Therefore, (z(n)) tends to zero as n → ∞, that is, L = 0, which contradicts L > 0. Hence L = 0. Taking into account the fact that the sequence (z(n)) is strictly decreasing, it is obvious that z(n) > 0. Hence, for every ϵ > 0 there exists a natural number n₄ such that for every n ≥ n₄

()

For sufficiently large n, after m-steps we obtain

()

As n → ∞, clearly m → ∞, and therefore

()

Since ϵ is an arbitrary real positive number and, taking into account the fact that (x(n)) > 0, it is clear that

()

Let c = 0. In view of part (iii) of Lemma 2.1, we have

()

This guarantees that (z(n)) is bounded, and therefore, since z(n) = x(n), (x(n)) is bounded. Also, since (z(n)) is stricly decreasing, lim _n→∞z(n) exists, that is, lim _n→∞x(n) exists. In view of (2.18), we conclude that

()

Assume that 0 < c < 1, then

()

Therefore,

()

which means that L = 0. Hence,

()

and since

()

we have

()

The proof of part (III) of the theorem is complete.

Assume that c ≥ 1. In view of Part (iii) of Lemma 2.1, it is clear that which combined with (2.14) implies that (z(n)) is bounded and, therefore (x(n)) is bounded. The proof of part (IV) of the theorem is complete.

In the remainder of this proof, it will be assumed that x(n) is a continuous function with respect to c, and, therefore, instead of x(n) we will write x(c, n).

Let c = −1. Then, in view of part (II), (x(−1, n)) oscillates. On the other hand, since x(c, n) is continuous, we have

()

But x(c, n) > 0 for all large n, and therefore its limit is always nonnegative. Thus, x(−1, n) > 0 for all large n which contradicts that (x(−1, n)) oscillates. Therefore, x(−1, n) = 0 eventually.

Let c < −1. In view of part (I) we have (x(c, n)) is unbounded, and therefore x(c, τ(n)) → ∞. Let M > 0, then there exists an index n₅ such that, for every n ≥ n₅, x(c, τ(n)) > M. Since the function x(c, n) is continuous, x(c, τ(n)) is continuous, and therefore

()

Hence, there exists h > 0 so that, if c > −1 − h then x(c, τ(n)) < M for every n ≥ n₅, which contradicts x(c, τ(n)) > M. This implies that, there exists an interval (a, −1) such that

()

Let

()

Then, with the same argument as above, we conclude that

()

So, by a similar procedure we obtain an interval (B, A] such that

()

This contradicts our assumption for A. Thus, if c < −1, we have x(c, n) = 0 eventually. The proof of part (V) of the theorem is complete.

Assume that −1 < c ≤ 1. Taking into account part (III), it is enough to show part (VI) only for c = 1. In view of parts (iii) and (i) of Lemma 2.1, we have

()

Assume, for the sake of contradiction, that L > 0. Taking into account the fact that lim _n→∞x(c, n) = 0 when 0 < c < 1, there exists n₆ ∈ ℕ such that, for every n ≥ n₆, we have

()

and, since x(c, τ(σ(n))) is continuous,

()

Hence,

()

which contradicts lim _n→∞x(c, τ(σ(n))) = L. Therefore, L > 0 is impossible. Thus, L = 0, and, in view of (2.8), we conclude that

()

which means that

()

The proof of part (VI) of the theorem is complete.

Finally, since x(c, n) has convergent Taylor series, we have

()

Choose a < −1. Then x^(m)(a, n) = 0 and, therefore, x(c, n) = 0. The proof of part (VII) of the theorem is complete.

The proof of the theorem is complete.

By way of illustration and for purely pedagogical purposes, the asymptotic behavior of nonoscillatory solutions of (E) is presented in Figure 1.

Description unavailable — **Figure 1**
Open in figure viewer PowerPoint

Corollary 3.2. For (E1) one has the following.

(i)
Every nonoscillatory solution tends to ±∞ if c < −1.
(ii)
Every solution oscillates if c = −1.
(iii)
Every nonoscillatory solution tends to zero if c > −1.

Furthermore, if any solution of (E1) is continuous with respect to c, one has the following.

(iv)
Every solution is zero if c ≤ −1.
(v)
If, additionally, any solution of (E1) has continuous derivatives of any order and convergent Taylor series for every c ∈ ℝ, then the solution is zero.

Proof. In part (I) of Theorem 3.1 we have proved that

()

and consequently

()

which means that

()

The proof of part (i) of the corollary is complete.

Part (ii) is direct from part (II) of Theorem 3.1.

As we have proved in parts (III) and (IV) of Theorem 3.1, if c > −1, then

()

and consequently

()

which means that

()

The proof of part (iii) of the corollary is complete.

Parts (iv) and (v) are direct from parts (V) and (VII) of Theorem 3.1.

The proof of the corollary is complete.

References

1 Driver R. D., Existence and continuous dependence of solutions of a neutral functional-differential equation, Archive for Rational Mechanics and Analysis. (1965) 19, 149–166, 0179406, https://doi.org/10.1007/BF00282279, ZBL0148.05703.
10.1007/BF00282279
Google Scholar
2 Bellman R. and Cooke K. L., Differential-Difference Equations, 1963, Academic Press, New York, NY, USA, 0147745.
10.1063/1.3050672
Google Scholar
3 Hale J., Theory of Functional Differential Equations, 1977, 2nd edition, Springer, New York, NY, USA, 0508721.
10.1007/978-1-4612-9892-2
Web of Science® Google Scholar
4 Snow W., Existence, Uniqueness, and Stability for Nonlinear Differential-Difference Equations in the Neutral Case, 1965, New York: Courant Institute of Mathematical Sciences, New York University, New York, NY, USA, IMM-NYU 3282614521.
Google Scholar
5 Agarwal R. P., Bohner M., Grace S. R., and O′D′Regan D., Discrete Oscillation Theory, 2005, Hindawi Publishing Corporation, New York, NY, USA, https://doi.org/10.1155/9789775945198, 2179948, ZBL1211.90152.
10.1155/9789775945198
Google Scholar
6 Bellen A., Guglielmi N., and Ruehli A. E., Methods for linear systems of circuit delay differential equations of neutral type, IEEE Transactions on Circuits and Systems. I. (1999) 46, no. 1, 212–216, 1683187, https://doi.org/10.1109/81.739268, ZBL0952.94015.
10.1109/81.739268
Web of Science® Google Scholar
7 Balanov A. G., Janson N. B., McClintock P. V. E., Tucker R. W., and Wang C. H. T., Bifurcation analysis of a neutral delay differential equation modelling the torsional motion of a driven drill-string, Chaos, Solitons and Fractals. (2003) 15, no. 2, 381–394, https://doi.org/10.1016/S0960-0779(02)00105-4.
10.1016/S0960-0779(02)00105-4
Web of Science® Google Scholar
8 Gopalsamy K., Stability and Oscillations in Population Dynamics, 1992, 74, Kluwer Academic Publishers, Boston, Mass, USA, 1163190.
Google Scholar
9 Tang X. H. and Cheng S. S., Positive solutions of a neutral difference equation with positive and negative coefficients, Georgian Mathematical Journal. (2004) 11, no. 1, 177–185, 2065549, ZBL1059.39009.
10.1515/GMJ.2004.177
Google Scholar
10 Xiong W. and Liang J., Novel stability criteria for neutral systems with multiple time delays, Chaos, Solitons and Fractals. (2007) 32, no. 5, 1735–1741, 2299088, https://doi.org/10.1016/j.chaos.2005.12.020, ZBL1146.34330.
10.1016/j.chaos.2005.12.020
Web of Science® Google Scholar
11 Zhou J., Chen T., and Xiang L., Robust synchronization of delayed neural networks based on adaptive control and parameters identification, Chaos, Solitons & Fractals. (2006) 27, 905–913.
10.1016/j.chaos.2005.04.022
Web of Science® Google Scholar
12 Driver R. D., A mixed neutral system, Nonlinear Analysis. (1984) 8, no. 2, 155–158, https://doi.org/10.1016/0362-546X(84)90066-X, 734448, ZBL0553.34042.
10.1016/0362-546X(84)90066-X
Web of Science® Google Scholar
13 Brayton R. K. and Willoughby R. A., On the numerical integration of a symmetric system of difference-differential equations of neutral type, Journal of Mathematical Analysis and Applications. (1967) 18, 182–189, 0213061, https://doi.org/10.1016/0022-247X(67)90191-6, ZBL0155.47302.
10.1016/0022-247X(67)90191-6
Web of Science® Google Scholar
14 Grammatikopoulos M. K., Grove E. A., and Ladas G., Oscillations of first-order neutral delay differential equations, Journal of Mathematical Analysis and Applications. (1986) 120, no. 2, 510–520, 864767, https://doi.org/10.1016/0022-247X(86)90172-1, ZBL0566.34056.
10.1016/0022-247X(86)90172-1
Web of Science® Google Scholar
15 Stavroulakis I. P., Oscillations of mixed neutral equations, Hiroshima Mathematical Journal. (1989) 19, no. 3, 441–456, 1035136, ZBL0712.34078.
10.32917/hmj/1206129285
Google Scholar
16 Baštinec J., Berezansky L., Diblík J., and Šmarda Z., A final result on the oscillation of solutions of the linear discrete-delayed equation Δx(n) = −p(n)x(n − k) with a positive coeffficient, Abstract and Applied Analysis. (2011) 2011, 28, 586328.
10.1155/2011/586328
Google Scholar
17 Baštinec J., Diblík J., and Šmarda Z., Existence of positive solutions of discrete linear equations with a single delay, Journal of Difference Equations and Applications. (2010) 16, no. 9, 1047–1056, 2722821, https://doi.org/10.1080/10236190902718026, ZBL1207.39014.
10.1080/10236190902718026
Web of Science® Google Scholar
18 Baštinec J., Diblík J., and Šmarda Z., Oscillations of solutions of a linear second order discrete-delayed equation, Advances in Difference Equations. (2010) 2010, 12, https://doi.org/10.1155/2010/693867, 693867.
10.1186/1687-1847-2010-693867
Google Scholar
19 Bezeransky A., Diblík J., Ruzickova M., and Suta Z., Asymtotic convergence of the solutions of a discrete equation with delays in the critical case, Abstract and Applied Analysis. (2011) 2011, 15, https://doi.org/10.1155/2011/709427, 709427.
10.1155/2011/709427
Google Scholar
20 Chatzarakis G. E., Karakostas G. L., and Stavroulakis I. P., Convergence of the positive solutions of a nonlinear neutral difference equation, Nonlinear Oscillations. (2011) 14, no. 3, 407–418.
Google Scholar
21 Chen M.-P., Lalli B. S., and Yu J. S., Oscillation in neutral delay difference equations with variable coefficients, Computers & Mathematics with Applications. (1995) 29, no. 3, 5–11, https://doi.org/10.1016/0898-1221(94)00223-8, 1326277, ZBL0819.39004.
10.1016/0898-1221(94)00223-8
Web of Science® Google Scholar
22 Cheng S. S. and Lin Y.-Z., Complete characterizations of an oscillatory neutral difference equation, Journal of Mathematical Analysis and Applications. (1998) 221, no. 1, 73–91, 1619135, https://doi.org/10.1006/jmaa.1997.5341, ZBL0911.39004.
10.1006/jmaa.1997.5341
Web of Science® Google Scholar
23 Diblík J. and Ružičková M., Convergence of the solutions of the equation y^′(t) = β(t)[y(t − δ) − y(t − τ)] in the critical case, Journal of Mathematical Analysis and Applications. (2007) 331, 1361–1370.
Web of Science® Google Scholar
24 Diblík J., Ružičková M., and Šmarda Z., Ważewski′s method for systems of dynamic equations on time scales, Nonlinear Analysis: Theory, Methods and Applications. (2009) 71, no. 12, e1124–e1131, https://doi.org/10.1016/j.na.2009.01.098.
10.1016/j.na.2009.01.098
Web of Science® Google Scholar
25 Diblík J., Ružičková M., and Šutá Z., Asymptotical convergence of the solutions of a linear differential equation with delays, Advances in Difference Equations. (2010) 2010, 12, 749852, 2660941, ZBL1203.34122, https://doi.org/10.1155/2010/749852.
10.1186/1687-1847-2010-749852
Google Scholar
26 Dong J.-G., Oscillation of solutions for first order neutral differential equations with distributed deviating arguments, Computers & Mathematics with Applications. (2009) 58, no. 4, 784–790, 2554022, https://doi.org/10.1016/j.camwa.2009.06.003, ZBL1189.34131.
10.1016/j.camwa.2009.06.003
Web of Science® Google Scholar
27 Domshlak Y., Partsvania N., and Stavroulakis I. P., Oscillation properties of first order neutral differential equations near the critical states, Nonlinear Functional Analysis and Applications. (2004) 9, no. 2, 173–184, 2071533, ZBL1069.34092.
Google Scholar
28 Gao Y. and Zhang G., Oscillation of nonlinear first order neutral difference equations, Applied Mathematics E-Notes. (2001) 1, 5–10, 1833830, ZBL0977.39009.
Google Scholar
29 Georgiou D. A., Grove E. A., and Ladas G., Oscillations of neutral difference equations, Applicable Analysis. (1989) 33, no. 3-4, 243–253, https://doi.org/10.1080/00036818908839876, 1030111, ZBL0685.39003.
10.1080/00036818908839876
Google Scholar
30 Győri I. and Horváth L., Asymptotic constancy in linear difference equations: limit formulae and sharp conditions, Advances in Difference Equations. (2010) 2010, 20, 789302, 2652453, https://doi.org/10.1155/2010/789302.
10.1186/1687-1847-2010-789302
Google Scholar
31 Gong X., Zhong X., Jia J., Quyang R., and Han H., Oscillation of first-order neutral difference equation, Modern Applied Science. (2009) 3, no. 8, 90–94.
10.5539/mas.v3n8p90
Google Scholar
32 Huong D. C., Oscillation and Convergence for a neutral difference equation, Journal of Science, Mathematics-Physics. (2008) 24, 133–143.
Google Scholar
33 Jia J., Zhong X., Gong X., Quyang R., and Han H., Nonoscillation of first-order neutral difference equation, Modern Applied Science. (2009) 3, no. 11, 30–33.
10.5539/mas.v3n11p30
Google Scholar
34 Ladas G. and Sficas Y. G., Oscillations of neutral delay differential equations, Canadian Mathematical Bulletin. (1986) 29, no. 4, 438–445, https://doi.org/10.4153/CMB-1986-069-2, 860851, ZBL0566.34056.
10.4153/CMB-1986-069-2
Web of Science® Google Scholar
35 Lalli B. S., Oscillation theorems for neutral difference equations, Computers & Mathematics with Applications. (1994) 28, no. 1–3, 191–202, Advances in difference equation1284234, https://doi.org/10.1016/0898-1221(94)00107-3, ZBL0812.39002.
10.1016/0898-1221(94)00107-3
Web of Science® Google Scholar
36 Lalli B. S. and Zhang B. G., On existence of positive solutions and bounded oscillations for neutral difference equations, Journal of Mathematical Analysis and Applications. (1992) 166, no. 1, 272–287, 1159653, https://doi.org/10.1016/0022-247X(92)90342-B, ZBL0763.39002.
10.1016/0022-247X(92)90342-B
Web of Science® Google Scholar
37 Li J. W., Wang Z. C., and Zhang H. Q., Oscillation of neutral delay difference equations, Differential Equations and Dynamical Systems. (1996) 4, no. 1, 113–121, 1652834, ZBL0871.39004.
Google Scholar
38 Migda M. and Zhang G., On unstable neutral difference equations with “maxima”, Mathematica Slovaca. (2006) 56, no. 4, 451–463, 2267766, ZBL1141.39002.
Google Scholar
39 Marian S. L., Loganathan M. P., and Selvan A. G. M., Oscillatory behavior of forced neutral difference equations with positive and negative coefficients, International Journal of Computational and Applied Mathematics. (2010) 5, 253–265.
Google Scholar
40 Öcalan O., Oscillation criteria for forced neutral difference equation with positive and negative coefficients, Dynamics of Continuous, Discrete & Impulsive Systems. (2008) 15, no. 2, 151–161, 2400635, ZBL1147.39003.
Google Scholar
41 Öcalan O. and Duman O., Oscillation analysis of neutral difference equations with delays, Chaos, Solitons and Fractals. (2009) 39, no. 1, 261–270, 2504564, https://doi.org/10.1016/j.chaos.2007.01.094, ZBL1197.39004.
10.1016/j.chaos.2007.01.094
Web of Science® Google Scholar
42 Péics H., Positive solutions of neutral delay difference equation, Novi Sad Journal of Mathematics. (2005) 35, no. 2, 111–122, 2244836.
Google Scholar
43 Sficas Y. G. and Stavroulakis I. P., Necessary and sufficient conditions for oscillations of neutral differential equations, Journal of Mathematical Analysis and Applications. (1987) 123, no. 2, 494–507.
10.1016/0022-247X(87)90326-X
Web of Science® Google Scholar
44 Shan W. and Weigao G., Oscillation of neutral difference equations with positive and negative coefficients, Computers & Mathematics with Applications. (2004) 47, no. 10-11, 1647–1657, 2079871, https://doi.org/10.1016/j.camwa.2004.06.012, ZBL1066.39012.
10.1016/j.camwa.2004.06.012
Web of Science® Google Scholar
45 Tang X. H. and Lin X., Necessary and sufficient conditions for oscillation of first-order nonlinear neutral difference equations, Computers & Mathematics with Applications. (2008) 55, no. 6, 1279–1292, 2394367, https://doi.org/10.1016/j.camwa.2007.06.009, ZBL1200.39004.
10.1016/j.camwa.2007.06.009
Web of Science® Google Scholar
46 Thandapani E., Arul R., and Raja P. S., Oscillation of first order neutral delay difference equations, Applied Mathematics E-Notes. (2003) 3, 88–94, 1980570, ZBL1027.39003.
Google Scholar
47 Thandapani E. and Kumar P. M., Oscillation and nonoscillation of nonlinear neutral delay difference equations, Tamkang Journal of Mathematics. (2007) 38, no. 4, 323–333, 2388783, ZBL1149.39008.
10.5556/j.tkjm.38.2007.66
Google Scholar
48 Tian C.-J. and Cheng S. S., Oscillation criteria for delay neutral difference equations with positive and negative coefficients, Bulletin of Mathematical Society of Paraná. (2003) 21, no. 1-2, 1–12, https://doi.org/10.5269/bspm.v21i1-2.7504, 2066945, ZBL1085.39013.
10.5269/bspm.v21i1?2.7504
Google Scholar
49 Yu J. S. and Wang Z. C., Asymptotic behavior and oscillation in neutral delay difference equations, Funkcialaj Ekvacioj. (1994) 37, no. 2, 241–248, 1299863, ZBL0808.34083.
Google Scholar
50 Zhang G., Oscillation for nonlinear neutral difference equations, Applied Mathematics E-Notes. (2002) 2, 17–19, 1979405, ZBL0997.39004.
Google Scholar
51 Zhang G. and Cheng S. S., Oscillation criteria for a neutral difference equation with delay, Applied Mathematics Letters. (1995) 8, no. 3, 13–17, https://doi.org/10.1016/0893-9659(95)00022-I, 1356800, ZBL0826.34065.
10.1016/0893-9659(95)00022-I
Web of Science® Google Scholar
52 Zhou Y., Oscillations of neutral difference equations, Kyungpook Mathematical Journal. (1999) 39, 283–291.
Google Scholar

Citing Literature

All articles

Convergence and Divergence of the Solutions of a Neutral Difference Equation

Abstract

1. Introduction

2. Some Preliminaries

3. Main Results

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Convergence and Divergence of the Solutions of a Neutral Difference Equation

Abstract

1. Introduction

2. Some Preliminaries

3. Main Results

References

Citing Literature

Figures

References

Related

Information