International Journal of Mathematics and Mathematical Sciences
Volume 2011, Issue 1 257903
Research Article
Open Access

Analytical Method in Solving Flow of Viscoelastic Fluid in a Porous Converging Channel

M. Esmaeilpour, 

Corresponding Author

M. Esmaeilpour

Department of Mechanical Engineering, Islamic Azad University, Nowshahr-Branch, Nowshahr, Iran iau.ac.ir

Search for more papers by this author
Naeem Roshan, 

Naeem Roshan

Department of Mechanical Engineering, Babol Noshirvani University of Technology, Babol, Iran nit.ac.ir

Search for more papers by this author
Negar Roshan, 

Negar Roshan

Computer Engineering Department, Amir-Kabir University of Technology, Tehran, Iran nit.ac.ir

Search for more papers by this author
D. D. Ganji, 

D. D. Ganji

Department of Mechanical Engineering, Babol Noshirvani University of Technology, Babol, Iran nit.ac.ir

Search for more papers by this author
First published: 23 May 2011
https://doi.org/10.1155/2011/257903
Citations: 3
Academic Editor: Mónica Clapp

Abstract

An analytical method, called homotopy perturbation method (HPM), is used to compute an approximation to the solution of the nonlinear differential equation governing the problem of two-dimensional and steady flow of a second-grade fluid in a converging channel. The table and figures are presented for influencing various parameters on the velocity field. The results compare well with those obtained by the numerical method. The method is straightforward and concise, and it can also be applied to other nonlinear evolution equations in mathematical physics.

1. Introduction

In recent years, there has been a considerable interest in the channel flow of non-Newtonian fluid because of its various applications in different fields of engineering. The problem of laminar flow of a viscous fluid in a parallel-walled channel was first studied by Berman [1] for two-dimensional case and the case of very cross-flow Reynolds number. In 1963, Rosenhead [2] explained this phenomenon more adequately by the theory of converging and diverging channel with a permeable wall and suction or injection at the wall whose magnitude is inversely proportional to the distance along the wall from the origin of the channel. Terrill [3] presented the new form for channel flow and considered suction at one wall and injection at the other wall where the rates of this injection and suction were equal. Some other researchers continued the solution of this phenomenon for different cases [4–7]. In 2001, Baris restated Terrill’s problem by introducing a second-grade fluid and presented the effect of the elasticity of the fluid on the velocity distribution for different values of Reynolds number and cross-flow Reynolds number [8].

In all of these cases, these problems do not admit analytical solution, so these equations should be solved using special techniques. In recent years, much attention has been devoted to the newly developed methods to construct an analytic solution of equation; such methods include the Adomian decomposition method [9–12], the homotopy perturbation method (HPM) [13–24], and the variational iteration method (VIM) [25–31]. HPM is the most effective and convenient one for both linear and nonlinear equations. This method does not depend on a small parameter. Using homotopy technique in topology, a homotopy is constructed with an embedding parameter p ∈ [0,1], which is considered as a “small parameter.” HPM has been shown to effectively, easily, and accurately solve a large class of linear and nonlinear problems with components converging rapidly to accurate solutions. HPM was first proposed by He [14–19] and was successfully applied to various engineering problems.

The organization of this paper is as follows: in Section 2, the mathematical framework of the homotopy perturbation method is illustrated. To present a clear overview of this method, Section 3 contains the description of the laminar flow of a second-grade viscoelastic fluid in a porous converging channel of total opening of 60°. In Section 4, this analytical method is utilized to solve the nonlinear equation governing the described problem. Finally, some results are provided.

2. Fundamentals of the Homotopy Perturbation Method

To illustrate the homotopy perturbation method (HPM) for solving nonlinear differential equations, He [14, 15] considered the following non-linear differential equation:
(2.1)
with the boundary condition of
(2.2)
where A is a general differential operator, B is a boundary operator, f(r) is a known analytic function, Γ is the boundary of the domain Ω, and ∂(  )/∂n denotes differentiation along the normal vector drawn outwards from Ω. The operator A can generally be divided into two parts L and N, where L is linear and N is nonlinear. Therefore, (2.1) can be rewritten as follows:
(2.3)
Homotopy perturbation structure is shown as follows:
(2.4)
where
(2.5)
Equation (2.4) is equivalent to
(2.6)
So, we have
(2.7)
The changing process of p  from zero to unity is just that of H(v, p) from L(v) − L(u0) to A(v) − f(r). In topology, this is called deformation and L(v) − L(u0) and L(v) − L(u0) are called homotopic. According to the homotopy perturbation method, the parameter p is used as a small parameter, and the solution of (2.4) can be expressed as a series in p in the form of
(2.8)
When p → 1, (2.4) corresponds to the original one and (2.5) and (2.8) become the approximate solution of (2.3), that is,
(2.9)
The convergence of the series in (2.9) is discussed by He in [14, 15].

3. Problem Statement and Mathematical Formulation

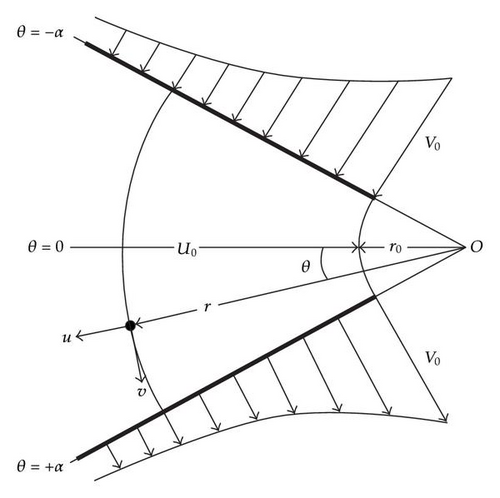
In this section, we state the problem and present the governing equation. The phenomenon of two-dimensional non-Newtonian viscoelastic fluid flow in a converging channel whose wall has suction and injection is considered. The rates of these suction and injection in two walls are equal and vary in inverse proportion to the distance along the wall from the center of the channel. We assume that the wall which has suction is located in θ = +α and the other wall which has injection of fluid is in θ = −α (Figure 1). According to Figure 1, u(r, θ) and ν(r) are velocity components in the directions of r and θ, respectively.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Schematic diagram of the physical system.
The governing equations for this problem are

  • continuity equation:

(3.1)

  • Momentum equation:

(3.2)
where V is the velocity, ρ is the density, and T is The Cauchy stress tensor [5, 9] and it is presented as follows:
(3.3)
Terrill and Roy and Nayak presented velocity field in the form of [3, 6]
(3.4)
where V0 is the velocities of suction and injection at θ = +α and θ = −α, respectively, at the typical length of r0. Also, U0 is the magnitude of the velocity in the direction of r at the center line of the channel.
The boundary conditions for this problem are
(3.5)
Using (3.1)–(3.5), we will have
(3.6)
where, in these equations, prime denotes derivation with respect to θ and ν   is the kinematic viscosity. Using (3.6) and eliminating the pressure term, (3.1) and (3.2) reduce to the following ordinary differential equation or similarity equation:
(3.7)
where R, Re, and N  are the cross-flow Reynolds number, Reynolds number, and elastic number, respectively.
The boundary conditions for this equation are
(3.8)

Equation (3.7) with the boundary conditions (3.8) is solved numerically by Bariş [9] for different cases of R, Re, and N. In this paper, we reconsider the governing equation and solve it by He’s homotopy perturbation method.

4. HPM Solutions for Velocity and Temperature Fields

In this section, we will solve (3.7) using HPM. So, we construct the following homotopy for these equations:
(4.1)
According to the definition of the HPM, we consider function f(θ) as follows:
(4.2)
Assuming substituting f(θ) from (4.2) into (4.1), and using some simplification and rearranging based on powers of p-terms, we have
(4.3)
(4.4)
(4.5)
(4.6)
(4.7)
(4.8)
By using Maple software, we solve (4.3), (4.5), and (4.7) with considering boundary conditions (4.4), (4.6), and (4.8). We have obtained the 4-term approximations to f(θ), but for lack of space, only the first 3 terms produced are given below
(4.9)
According to the definition of the HPM in Section 2 ((2.8) and (2.9)), we consider 4-order solution of f(θ) as following:
(4.10)
In the case of  Re = 3,  R = 5, and N = 0.015 (Table 1), functions f(θ) are
(4.11)
Table 1. The results of HPM and NM methods for Re = 3, R = 5, and N = 0.015.
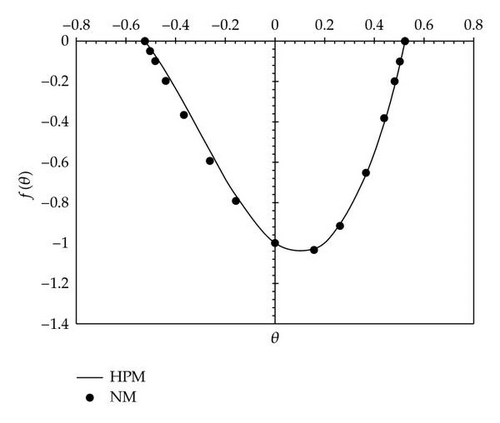
θ fHPM fNM |  fNM − fHPM|
−π/6 0.000024651 0.000000000 0.000025
−0.5235 −0.000133055 −0.000232980 0.000100
−0.5027 −0.034635498 −0.049303900 0.014668
−0.4817 −0.071891003 −0.098813000 0.026922
−0.4398 −0.152402362 −0.197161000 0.044759
−0.3665 −0.307655871 −0.366006250 0.058350
−0.2617 −0.542915584 −0.593305700 0.050390
−0.1571 −0.764703592 −0.791658300 0.026955
0.0000 −1.000000000 −1.000000000 0.000000
0.1571 −1.028797379 −1.034518440 0.005721
0.2617 −0.905274553 −0.915206190 0.009932
0.3665 −0.659877151 −0.652557500 0.007320
0.4398 −0.405545492 −0.381704720 0.023841
0.4817 −0.221073168 −0.198909090 0.022164
0.5027 −0.115346628 −0.100998040 0.014349
0.5235 −0.000482123 −0.000485050 0.000003
+π/6 0.000096447 0.000000000 0.000096

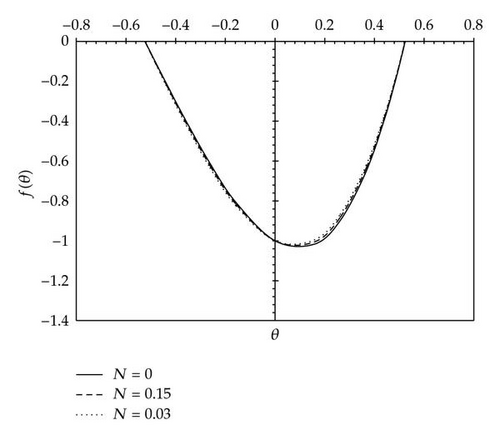
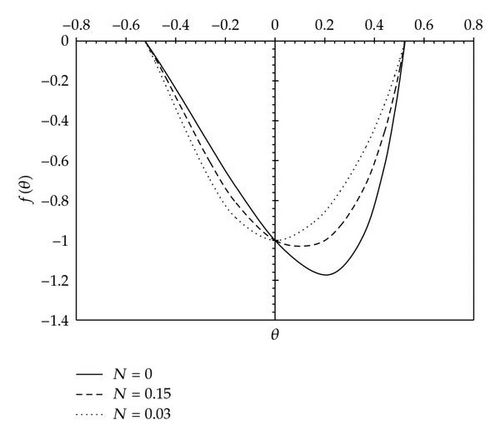
In the same manner, we have obtained the other cases for Re,  R, and N. The results are presented in Figures 2, 3, 4, and 5.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Comparison of HPM and the numerical method for  Re = 3, R = 5, and N = 0.015.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Velocity distribution for Re = 0.5, R = 2, and different N using HPM.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Velocity distribution for Re = 0.5, R = 5, and different N using HPM.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Velocity distribution for Re = 5, R = 2, and different N using HPM.

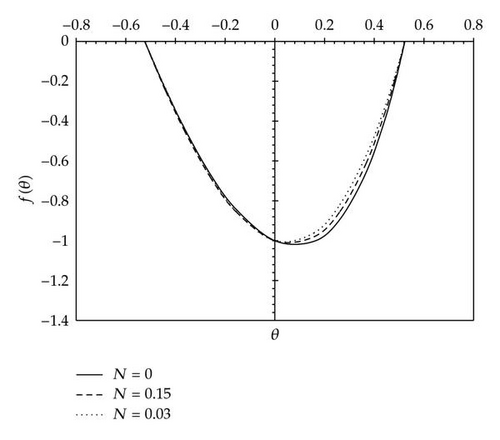
5. Conclusion

In this paper, we have successfully developed HPM to obtain the solutions of non-Newtonian viscoelastic fluid flow in a porous channel with suction and injection in their walls. The governing equation is solved for different cases of Reynolds number,  Re, the cross-flow Reynolds number, R, and elastic number, N. It is apparently seen that homotopy perturbation method is a very powerful and efficient technique for solving different kinds of problems arising in various fields of science and engineering and present a rapid convergence for the solutions.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.