Nonlinear Magnetoconvection in a Sparsely Packed Porous Medium
Abstract
Linear and weakly nonlinear properties of magnetoconvection in a sparsely packed porous medium are investigated. We have obtained the values of Takens-Bogdanov bifurcation points and codimension two bifurcation points by plotting graphs of neutral curves corresponding to stationary and oscillatory convection for different values of physical parameters relevant to magnetoconvection in a sparsely packed porous medium near a supercritical pitchfork bifurcation. We have derived a nonlinear two-dimensional Ginzburg-Landau equation with real coefficients by using Newell-Whitehead (1969) method. The effect of the parameter values on the stability mode is investigated and shown the occurrence of secondary instabilities namely, Eckhaus and Zigzag instabilities. We have studied Nessult number contribution at the onset of stationary convection. We have also derived two nonlinear one-dimensional coupled Ginzburg-Landau-type equations with complex coefficients near the onset of oscillatory convection at a supercritical Hopf bifurcation and discussed the stability regions of standing and travelling waves.
1. Introduction
Magnetoconvection in a porous medium uniformly heated from below is of considerable interest in geophysical fluid dynamics, as this phenomena may occur within the mushy layer of Earth′s outer core. Earth′s outer core consists of molten iron and lighter alloying element, sulphur in its molten form. This lighter alloying element present in the liquid phase is released as the new iron freezes due to supercooling onto the solid inner core. Hence we get mushy layer near the inner core boundary where the problem becomes convective instability in a porous medium [1]. The effect of geomagnetic field on the magnetoconvection instability is of interest in geophysics, particular in the study of Earth′s interior where the molten liquid Iron is electrically conducting, which can become convectively unstable as a result of differential diffusion.
In this paper we investigate the problem of magnetoconvection in a sparsely packed porous medium. The multiplicity of control parameters makes this system an interesting one for the study of hydrodynamic stability, bifurcation and turbulence [15]. Rudraiah [16] and Rudraiah and Vortmeyer [17] have studied both linear and steady nonlinear magnetoconvection in a sparsely packed porous medium using Brinkman model but they have taken effective viscosity μe same as fluid viscosity μ. However, experiments show that the ratio of effective viscosity μe to fluid viscosity μ takes the value ranging from 0.5 to 10.9 [18]. In Section 2, we write basic dimensionless equations in Boussinesq approximation for magnetoconvection in a sparsely packed medium by using a momentum equation with effective viscosity different from fluid viscosity. In Section 3, we study linear stability analysis. In Section 4.1, by using multiple-scale analysis of Newell and Whitehead [19], we derive two-dimensional nonlinear Ginzburg-Landau equation in complex amplitude A(X, Y, T) with real coefficients near the super critical pitchfork bifurcation. In Section 4.2, we show the occurrence of secondary instabilities such as Eckhaus instability and Zigzag instability. We have also considered the effect of Nusselt number on heat transport by magnetoconvection in a sparsely packed porous medium. In Section 5, we derive two nonlinear one-dimensional coupled Ginzburg-Landau type equations with complex coefficients near the onset of oscillatory convection at a supercritical Hopf bifurcation. Following Matthews and Rucklidge [20], we have dropped slow space dependence in X and obtained two coupled ordinary differential equations in A1R and A1L and discussed the stability regions of travelling and standing waves. By obtaining a one-dimensional Ginzburg-Landau equation in complex amplitude A(X, Y, T) with complex coefficients near a supercritical Hopf bifurcation, we have shown the condition for occurrence of Benjamin-Feir-type instability [21] for travelling and standing waves. In Section 6, we write conclusions of the paper.
2. Basic Equations
Boundary Conditions We assume that fluid is contained between z = 0 and z = 1, where z = 0 corresponds to boundary of solid iron core with Earth′s mushy layer and z = 1 corresponds to boundary of Earth′s mushy layer with Earth′s outer liquid core. For perfectly conducting boundary with temperature, we have
3. Linear Stability Analysis
3.1. Stationary Convection (ω = 0)
3.2. Oscillatory Convection (ω2 > 0)

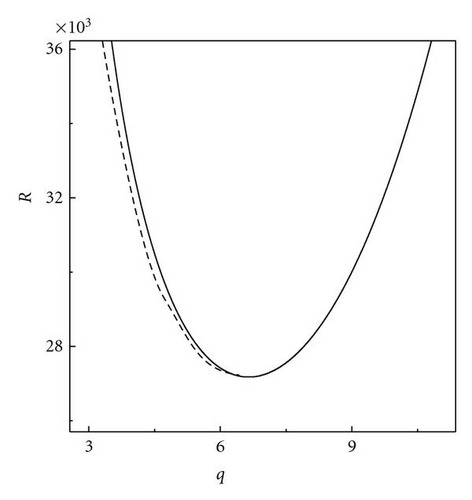
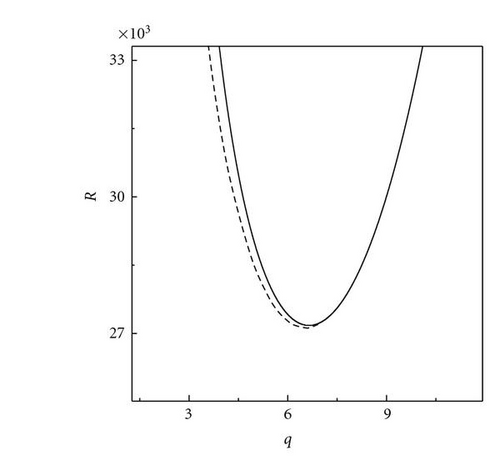
4. Onset of Stationary Convection at Supercritical Pitchfork Bifurcation
4.1. Derivation of Two-Dimensional Nonlinear Ginzburg-Landau Equation Using Newell-Whitehead [19] Method
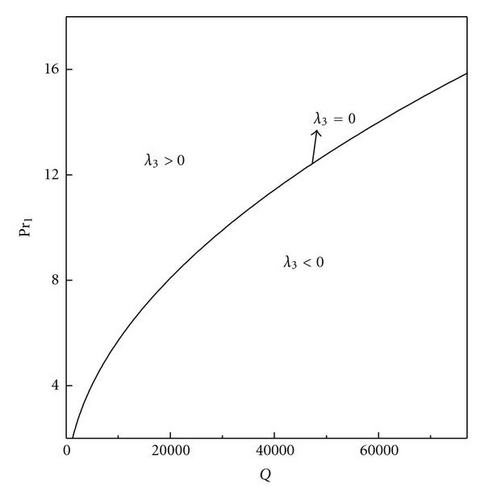
4.2. Long Wavelength Instabilities (Secondary Instabilities)
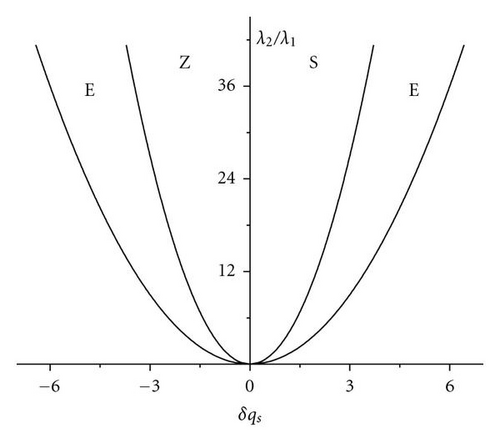
4.2.1. Longitudinal Perturbations and Eckhaus Instability
4.2.2. Transverse Perturbations and Zigzag Instability
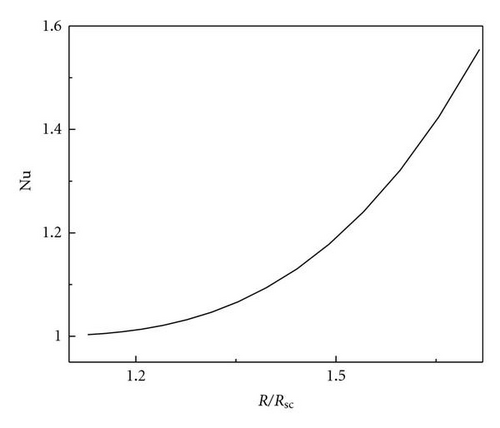
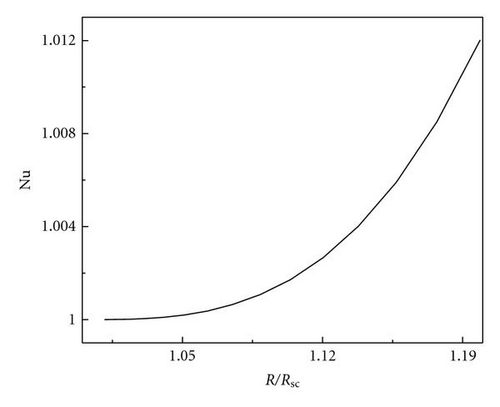
4.3. Heat Transport by Convection
5. Oscillatory Convection at the Supercritical Hopf Bifurcation
5.1. Travelling Wave and Standing Wave Convection
To study the stability regions of travelling waves and standing waves, Coullet et al. [24]. we proceed as follows.
If real parts of all eigenvalues of the Jacobian are negative at an equilibrium point, then that point is a stable equilibrium (Lyapunov′s theorem or principle of linearized stability). Some valuable conditions for travelling waves and standing waves are travelling waves are stable if β1 > 0, γ1 < 0 and δ1 < γ1 < 0. Standing waves are stable if β1 > 0, γ1 < 0 and (i) if δ1 > 0, then −γ1 > δ1 > 0 and (ii) if δ1 < 0, then −γ1 > −δ1 > 0.
The stability regions of travelling waves and standing waves are summarized in Figure 6. Here E is total amplitude and defined as . We do not distinguish between left travelling waves and right travelling waves. For rest state (steady state) E = 0, for travelling waves E = −β1/γ1, for standing waves E = −2β1/(γ1 + ς1). Travelling waves are supercritical if γ1 < 0 and standing waves are supercritical if γ1 + ς1 < 0. Figure 6(a) is drawn for stable travelling wave conditions and Figure 6(b) is drawn for stable standing wave conditions in (β1, E)-plane. The symbols (−, −) and (+, +) in Figures 6(a) and 6(b) indicate that both roots of Jacobian are negative and at least one root is positive between two roots. In Figures 6(a) and 6(b), travelling wave solution and standing wave solution bifurcate simultaneously from the steady-state solution (β1 ≥ 0 at this bifurcation point).
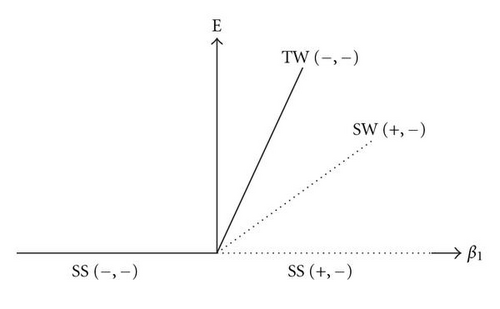
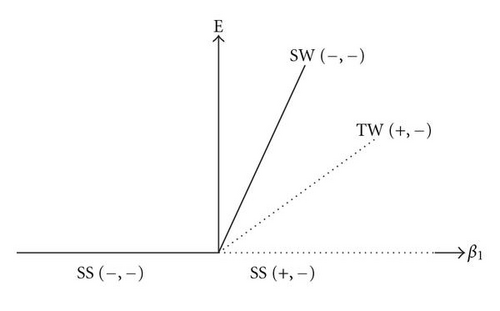
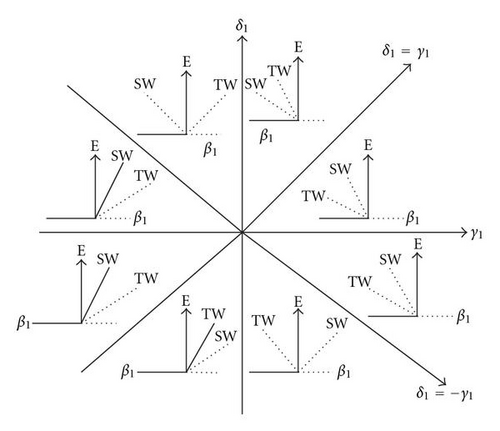
In these Figures 6(a) and 6(b), steady-state solution is stable for β1 < 0 and unstable β1 > 0. These figures show that for β1 > 0 both travelling waves and standing waves are supercritical. When travelling waves and standing waves bifurcate supercritically then at most one solution among travelling waves and standing waves will be stable. Thus, for β1 > 0 (Figure 6(a)) travelling waves are stable and (Figure 6(b)) standing waves are stable. In more detail we reproduce results of the stability analysis of equilibrium solutions in Figure 6(c), which is plotted in (γ1, ς1)-plane. From this figure we can observe that travelling waves are subcritical for γ1 > 0 and standing waves are subcritical for γ1 + ς1 > 0. In Figure 7, We study the stability regions of travelling waves and standing waves at the onset of Hopf bifurcation. The stability regions of standing waves and travelling waves increases when Pr2/Pr1 increases for fixed parameters. For a fixed Pr1 if we get initially travelling waves at the onset of oscillatory convection then they are replaced by standing waves as Q increases.
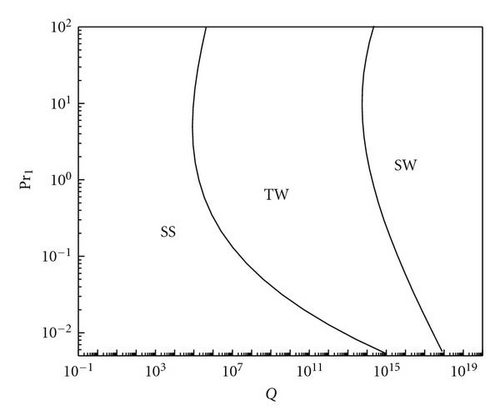
5.2. Long Wavelength Instabilities for the Onset of Travelling Wave Convection (Benjamin-Feir Instability)
6. Conclusions
In this paper we have considered both linear and weakly nonlinear analysis of magnetoconvection in a sparsely packed porous medium in Earth′s outer core by using free-free (stress-free) boundary conditions. Even though free-free boundary conditions cannot be achieved in laboratory, one can use it in geophysical fluid dynamic applications to Earth′s outer core since they allow simple trigonometric eigenfunctions. Our goal is to identify the region of parameter values, for which rolls emerge at the onset of convection.
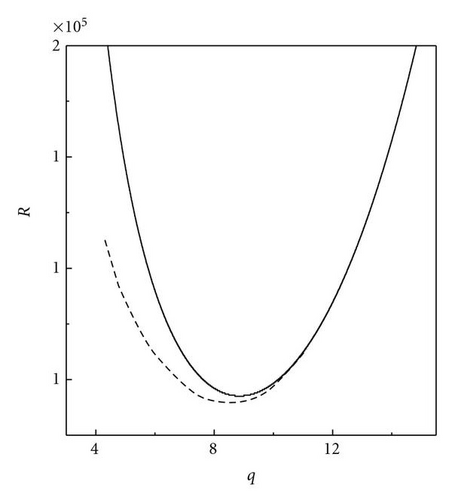
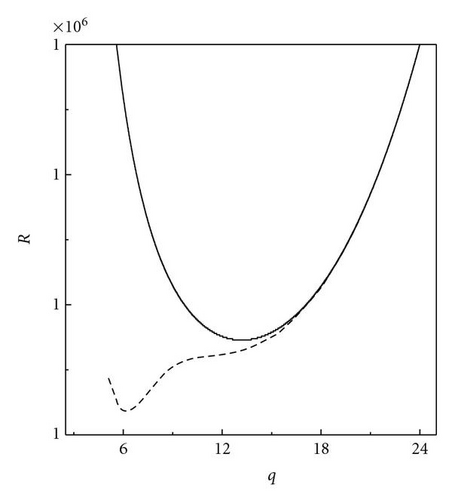
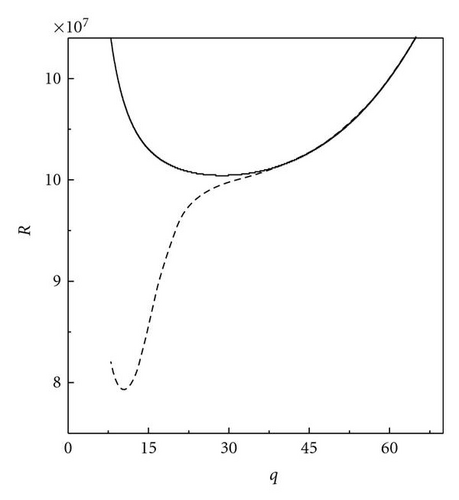
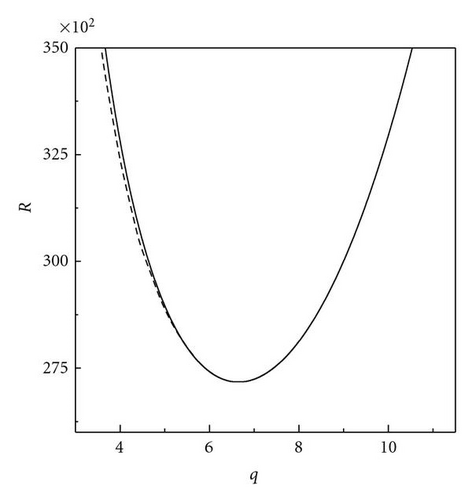
Following Chandrasekhar [2], we have described the stationary convection and oscillatory convection as curves Rs(q) and Ro(q, Pr2) versus wave numbers. The critical wave numbers for stationary convection and oscillatory convection are . For the problem of magnetoconvection in a sparsely packed porous medium, we get Takens-Bogdanov bifurcation point and codimension-two bifurcation point. In the case of linear theory both marginal and overstable motions are discussed. In Figures 1 and 2, is shown that the effect of Chandrasekhar number and porous parameter is to make the system more stable. By drawing stability boundaries in the Rayleigh number plane it is shown that the effect of magnetic field and porous parameter is to decrease the region of stabilities. In the nonlinear equation (60), λ0 = 0 gives the Takens-Bogdanov bifurcation point at qs = qsc and when λ0 = 0, (60) is not valid. The pitchfork bifurcation is supercritical if λ3 > 0 subcritical if λ3 < 0. and we get tricritical point if λ3 = 0. We have obtained from (60), long wave length instabilities, namely, Eckhaus and Zigzag instabilities. From (60) which is valid only for λ3 > 0, we have calculated Nusselt number Nu and studied heat transport by convection. We have also derived two one-dimensional nonlinear coupled Ginzburg-Landau type equations, namely, (98) at the onset of oscillatory convection at supercritical Hopf bifurcation. We have computed stability regions of SW and TW at both Hopf bifurcation. The conditions for SW and TW are AL = AR and AL = 0 or AR = 0, respectively. TW exist if |AL|2 = −β1/γ1 > 0 and they are supercritical if γ1 < 0. SW exist if |AL|2 = |AR|2 = −β1/(γ1 + δ1) > 0 and SW are supercritical if γ1 + δ1 < 0. When both SW and TW are supercritical then at most one equilibrium solution is stable. At Takens-Bogdanov bifurcation point we get both TW and SW. By deriving one-dimensional Ginzburg-Landau equations with complex coefficients, namely, (116) and (117), we have shown the existence of Benjamin-Feir-type of instability for both TW and SW. Near the Takens-Bogdanov bifurcation point the conducting state becomes unstable against both stationary and oscillatory mode, that is, the real parts of two eigenvalues pass through zero simultaneously. This violates the assumption made for deriving amplitude equations (60) and (98). Instead a new equation, which is second order in time, has to be used near the Takens-Bogdanov bifurcation point.




