The Modified Negative Decision Number in Graphs
Abstract
A mapping x : V → {−1,1} is called negative if ∑u∈N[v]x(u) ≤ 1 for every v ∈ V. The maximum of the values of ∑v∈Vx(v) taken over all negative mappings x, is called the modified negative decision number and is denoted by βD ′(G). In this paper, several sharp upper bounds of this number for a general graph are presented. Exact values of these numbers for cycles, paths, cliques and bicliques are found.
1. Introduction
Let G = (V, E) be a graph with vertex set V and edge set E. For a vertex v ∈ V, the open neighbourhood of v in G is N(v) = {u ∈ V∣uv ∈ E}, and N[v] = N(v)∪{v} is its closed neighbourhood. For a graph G, and a subset S⊆V, we let deg S(v) denote the number of vertices in S joined to v. In particular, deg V(v) = deg (v), the degree of v in G. For disjoint subsets S and T of vertices, we use E(S, T) for the set of edges between S and T, and let e(S, T) = |E(S, T)|. Let G[S] denote the subgraph of G induced by S. For an integer k ≥ 3, the bipartite graph K1,k is called a star, and the vertex of degree k is called the central vertex. Let x : V → ℝ be a real-valued function. For convenience, we write x(S) for ∑v∈Sx(v) for S⊆V.
In [1], we initiated the study of the negative decision number in a graph. A function x : V(G)→{−1,1} is called a bad function of G if x(N(v)) ≤ 1 for every v ∈ V(G). The maximum of the values of x(V(G)), taken over all bad functions f, is called the negative decision number and is denoted by βD(G).
The motivation for studying this parameter may be explained from a modelling perspective. For instance, by assigning the values −1 or 1 to the vertices of a graph, one can model networks of people in which global decisions must be made (e.g., positive or negative responses). In certain circumstances, a positive decision can be made only if there are significantly more people voting for than those voting against. We assume that each individual has one vote, and each has an initial opinion. We assign 1 to vertices (individuals) which have a positive opinion and −1 to vertices which have a negative opinion. A voter votes “good” if there are at least two more vertices in its open neighbourhood with positive opinion than with negative opinion, otherwise the vote is “bad”. We seek an assignment of opinions that guarantee a unanimous decision; namely, for which every vertex votes “bad”. Such an assignment of opinions is called a uniformly negative assignment. Among all uniformly negative assignments of opinions, we are particularly interested in the minimum number of vertices (individuals) which have a negative opinion. The negative decision number is the maximum possible sum of all opinions, 1 for a positive opinion and −1 for a negative opinion, in a uniformly negative assignment of opinions. The negative decision number corresponds to the minimum number of individuals who can have negative opinions and in doing so force every individual to vote bad.
In the present paper, we study a variation of the negative decision number in a graph. A mapping x : V → {−1,1} is called negative if ∑u∈N[v]x(u) ≤ 1 for every v ∈ V. The maximum of the values of ∑v∈Vx(v), taken over all negative mappings x, is called the modified negative decision number and is denoted by .
The parameter differs significantly from βD. For instance, for a cycle Cn of order n, βD(Cn)∈{−2, −1,0} ([1] see Theorem 5), while (see Corollary 2.6).
Throughout this paper, if x is a negative mapping of G, then we let P and Q denote the sets of those vertices of G which are assigned (under x) the values +1 and −1, respectively, and we let p = |P| and q = |Q|. Hence, x(V) = p − q.
All graphs considered in this paper are simple, finite, and undirected. For a general reference on graph theory, the reader is referred to [2, 3]. Notice that for two disjoint graphs G and H. Hence, we assume that all graphs are connected in this paper.
In the next section, we present several sharp upper bounds on the modified negative decision number for a general graph. We also establish sharp upper bounds on this number for bipartite graphs and regular graphs. Exact values of these numbers for cycles, paths, cliques, and bicliques are found.
2. Main Results
In this section, we investigate the modified negative decision number of a graph. We first present an upper bound on this number for a general graph in terms of its order.
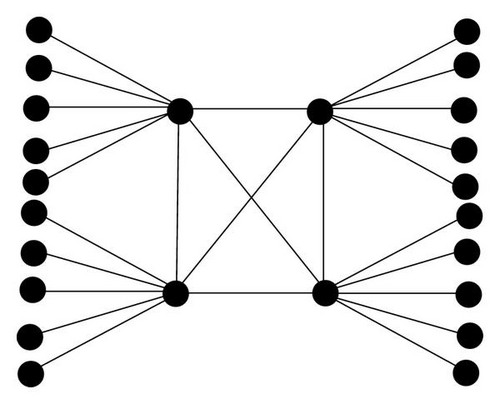
For this purpose, we define a family ℱ of graphs as follows. Let F3 = K1,2, and for k ≥ 4, let Fk be the graph obtained from the disjoint union of k stars K1,k+1 by adding all possible edges between the central vertices of the k stars. See Figure 1 for an example of F4. Let ℱ = {Fk∣k ≥ 3}.
Theorem 2.1. If G is a graph of order n ≥ 2, then
Proof. Let x be a negative mapping such that . Then . Note that every vertex in P must be joined to at least one vertex in Q. By the pigeonhole principle, at least one vertex v in Q is joined to at least |P | /|Q | = (n − q)/q vertices in P. Hence,
To see this bound is sharp, let G ∈ ℱ. Thus, G = Fk for some k ≥ 4. Hence, G has order n = k(k + 2), and so . Assigning the value −1 to each of the k central vertices of the stars, and +1 to all other vertices, we define a negative mapping x of G satisfying . Thus, . It follows that .
Next we give an upper bound of the modified negative decision number for a general graph in terms of its order and size.
Theorem 2.2. If G is a graph of order n ≥ 2 and size m, then
Proof. Let x be a negative mapping such that . Then . As every vertex in P must be joined to at least one vertex in Q, e(P, Q) ≥ p = n − q. For each vertex v of Q, deg Q(v) ≥ deg P(v) − 2, and hence,
In the following theorem, we establish an upper bound of the modified negative decision number for a bipartite graph in terms of its order and we characterize the graphs attaining this bound. We define a family ℋ of bipartite graphs as follows.
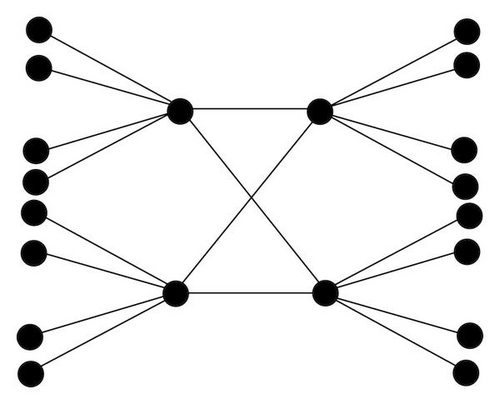
For k ≥ 1, let Hk be the bipartite graph obtained from the disjoint union of 2k stars K1,k+2 with centres {x1, x2, …, xk, y1, y2, …, yk} by adding all edges of the type xiyj, 1 ≤ i, j ≤ k. See Figure 2 for an example of H2. Let ℋ = {Hk∣k ≥ 1}.
Theorem 2.3. If G is a bipartite graph of order n ≥ 2, then
Proof. Let x be a negative mapping of G such that . Let X and Y be the partite sets of G. Further, let X+ and X− be the sets of vertices in X that are assigned the value +1 and −1 (under x), respectively. Let Y+ and Y− be defined analogously. Then P = X+ ∪ Y+ and Q = X− ∪ Y−. For convenience, let |X+ | = k, |X− | = s, |Y+ | = l and |Y− | = t. Hence, .
As every vertex in X+ must be joined to at least one vertex in Y−, by the pigeonhole principle, at least one vertex v in Y− is joined to at least |X+ | /|Y− | = k/t vertices in X+. Hence,
If , then by the above analysis, we have s = t and k = l = s(s + 2). Moreover, each vertex of X+ (resp., Y+) has degree 1 and is joined to one vertex of Y− (resp., X−), while each vertex of Y− is joined to all vertices of X− and s + 2 vertices of X+ and each vertex of X− is joined to all vertices of Y− and s + 2 vertices of Y+. Thus, implies that G ∈ ℋ.
If G ∈ ℋ, then G = Hk for some k ≥ 1. Hence, G has order n = 2k(k + 3), and so . Assigning to the k central vertices of the stars the value −1, and to all other vertices +1, we define a negative mapping x of G satisfying . Hence, . It follows that .
Finally, we present an upper bound of the modified negative decision number for a regular graph in terms of its order in Theorem 2.5. We encourage the reader to verify our next theorem first.
Theorem 2.4. For any integer n ≥ 2, one has
For a general k-regular graph, we have the following.
Theorem 2.5. If G is k-regular graph of order n, then
Proof. Let x be any negative mapping of G. As G is a k-regular graph,
Case 1. k is even. Since x is a negative mapping, for every vertex v ∈ V, x(N[v]) ≤ 1. By (2.20), it follows that
Case 2. k is odd. In this case, |N[v]| is even for every v ∈ V. So, for each v ∈ V, x(N[v]) ≤ 1 implies that x(N[v]) ≤ 0. Thus,
Corollary 2.6. For any integer n ≥ 3, one has
Proof. As Cn is a 2-regular graph, by Theorem 2.5, we have . Let v1, v2, …, vn be the n vertices of Cn in a clockwise order. We discuss the following three cases.
Case 1. n = 3k for some integer k. To show that , it suffices to show that there is a negative mapping x of Cn such that x(V(Cn)) = k. In fact, assigning +1, +1, −1 starting with v1 clockwise, and repeating, we produce a negative mapping x of Cn satisfying x(V(Cn)) = k.
Case 2. n = 3k + 2 for some integer k. To show that , it suffices to show that there is a negative mapping x of Cn such that x(V(Cn)) = k. In fact, if we assign 1,1, −1,1, −1 to the vertices in a clockwise order when n = 5, or assign 1,1, −1, …, 1,1, −1,1, −1 starting with v1 clockwise when n > 5, then we produce a negative mapping x of Cn satisfying x(V(Cn)) = k.
Case 3. n = 3k + 1 for some integer k. To show that , it suffices to show that there is a negative mapping x of Cn such that x(V(Cn)) = k − 1. In fact, if we assign 1, −1,1, −1 to the vertices in a clockwise order when n = 4, or assign 1,1, −1, …, 1,1, −1, −1 starting with v1 clockwise when n > 4, then we produce a negative mapping x of Cn satisfying x(V(Cn)) = k − 1.
To show , we let x be a negative mapping of Cn such that . So . Hence, p ≤ 2k, implying that .
Corollary 2.7. For any integer n ≥ 2, one has
Proof. It is easy to see that Corollary 2.7 is true for 2 ≤ n ≤ 4. So we may assume that n ≥ 5. Let v1, v2, …, vn be the n vertices of Pn with end vertices v1 and vn. We only show that . The rest of the proof is similar to that of Corollary 2.6, so is omitted.
Take any negative mapping x of Pn. For i = 1 or n, as deg (vi) = 1, we have that
Note that ∑v∈Vx(N[v]) = 3x(V) − x(v1) − x(vn). So,
For the biclique Kn,n, we have the following result.
Theorem 2.8. For any integer n ≥ 2, one has
Proof. Let X = {u1, u2, …, un} and Y = {v1, v2, …, vn} be the partite sets of Kn,n. As Kn,n is an n-regular graph, by Theorem 2.5, . Hence, . As Kn,n has order 2n, which is even,
To prove the case when n is even, it suffices to show that there exists a negative mapping x of Kn,n such that x(V(Kn,n)) = 0. In fact, we can produce such x by assigning x(vi) = x(ui) = (−1) i, 1 ≤ i ≤ n.
Now we prove the case when n is odd. Let x be a negative mapping of Kn,n such that . Let X+, X−, Y+, and Y− be defined the same as in the proof of Theorem 2.3. Then P = X+ ∪ Y+ and Q = X− ∪ Y−. Let |X+ | = k, |X− | = s, |Y+ | = l and |Y− | = t. Thus, . As , by (2.30), we have that
Notice that we may assume k ≤ s and l ≤ t. If k + l = s + t, then k = s and l = t contradicting to the fact k + s = l + t = n, where n is odd. Hence, .
To show that , it suffices to show that there is a negative mapping x of Kn,n such that x(V(Kn,n)) = −2. In fact, we can produce such x by assigning x(un) = −1, x(ui) = (−1) i−1 for 1 ≤ i ≤ n − 1 and x(vj) = (−1) j, 1 ≤ j ≤ n.




