Arnold′s Projective Plane and r-Matrices
Abstract
We will explain Arnold′s 2-dimensional (shortly, 2D) projective geometry (Arnold, 2005) by means of lattice theory. It will be shown that the projection of the set of nontrivial triangular r-matrices is the pencil of tangent lines of a quadratic curve on Arnold′s projective plane.
1. Introduction
We briefly describe Arnold′s projective geometry [1]. We recall the ordinary projective plane ℙ(ℝ3) over the real field. We replace ℝ3 to the set of the quadratic functions on the canonical symplectic plane (ℝ2 : p, q). The quadratic functions form into a Lie subalgebra of the canonical Poisson algebra on the symplectic plane. This Lie algebra is isomorphic to sl(2, ℝ); that is, Arnold introduced a projective plane ℙ(sl(2, ℝ)). By the projection, a (nontrivial) quadratic function corresponds to a point Q on the projective plane, and the Killing form on sl(2, ℝ) corresponds to a quadratic curve on the projective plane, because it is a symmetric bilinear form. Since the Killing form is nondegenerate, the associated curve defines a duality (so-called polar system) between the projective lines and the projective points. Arnold showed that the Poisson bracket corresponds to the pole point of the projective line through Q1 and Q2. As an application, it was shown that given a good triangle composed of three points (Q1, Q2, Q3), the three altitudes intersect the same point (altitude theorem). Interestingly, the altitude theorem is shown by the Jacobi identity (see Figure 1).
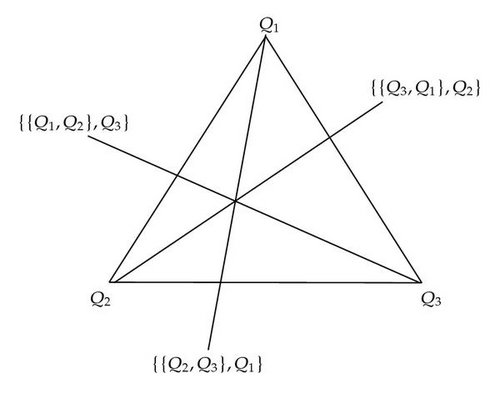
The monomials of double brackets correspond to the three bold lines, via the line-point duality. By the Jacobi identity, the three monomials are linearly dependent. This implies that the three lines intersect the same point.
We suppose that 2D projective geometry is encoded in the Lie algebra. However some information on the Lie algebra is lost in the process of constructing projective geometry; besides, it is not clear why it has to happen, conceptually. So we will reformulate the Arnold construction by means of lattice theory. Since the lattice is an algebra, the problem becomes more clear. We will prove, when the characteristic of the ground field is not 2, that each 3D simple Lie algebra admits a modular lattice structure. This proposition explains why 2D projective geometry can be encoded in sl(2).
It is crucial to consider the Plücker embedding for the algebraic Arnold construction. When 𝔤 is 3D and simple, the Lie algebra multiplication μ : 𝔤⋀𝔤 → 𝔤, x⋀y ↦ [x, y] is an isomorphism, which induces an isomorphism ℙ(𝔤⋀𝔤)≅ℙ(𝔤). We will show that the line-point duality on ℙ(𝔤) is equivalent with the isomorphism ℙ(𝔤⋀𝔤)≅ℙ(𝔤), up to the Plücker embedding.
As an application we study a projective geometry of triangular r-matrices, when 𝔤 = sl(2). We will prove that the projection of the set of nontrivial triangular r-matrices is equivalent to the pencil of tangent lines on the quadratic curve made from the Killing form. This proposition is equivalently translated as follows: the classical Yang-Baxter equation {r, r} = 0 on sl(2) is equivalent to the quadratic curve on the projective plane.
2. Algebraic Arnold Construction
2.1. Subspace Lattices
Example 2.1 (subspace lattices). Let V be a vector space. Consider the set of subspaces of V: Latt(V): = {S∣S ⊂ V}. Define two natural multiplications (cup- and cap-products) on Latt(V) by
The subspace lattices are complementary; that is, the zero space 0 is the unit element with respect to ⌣ and the total space V is ⌢. If V is split for each S, then there exists a cosubspace satisfying and . The subspace (resp., S) is called a complement1 of S (resp., ). Such a lattice is called a complemented lattice. If V is finite dimensional, then the subspace lattice is a complemented-modular-lattice. A projective geometry is axiomatically defined as a complemented-modular-lattice satisfying some additional properties.
Definition 2.2. When V is (n + 1)-dimensional, the subspace lattice Latt(V) is called an n-dimensional projective geometry over V.
The 1D subspaces are regarded as projective points, 2D subspaces are projective lines and so on. The zero space 0 is regarded as the empty set. For instance, given two 2D subspaces S1 and S2, the intersection S1⌢S2( = S1∩S2) is the common point of two projective lines (if it exists).
2.2. Lie Algebra Construction of Projective Plane
Let (𝔤, [−, −]) be a 3D 𝕂-Lie algebra with a nondegenerate symmetric invariant pairing (−, −), where 𝕂 is the ground field char(𝕂) ≠ 2. We assume that [𝔤, 𝔤] = 𝔤, or equivalently, the Lie bracket is an isomorphism from 𝔤⋀𝔤 to 𝔤. This assumption is needed in order to construct projective geometry. Such a Lie algebra is simple. In particular, when 𝕂 is a closed field, 𝔤 is isomorphic to sl(2, 𝕂).
We denote by p(x) the 1D subspace generated by x ∈ 𝔤 and denote by l(x, y) the 2D subspace generated by x, y ∈ 𝔤. We define new cup-and cap-products ⌣′ and ⌢′ on Latt(𝔤).
Definition 2.3 (Arnold products). (i) p(x)⌣′p(y): = p⊥([x, y]), p(x) ≠ p(y), where ⊥ means the orthogonal space with respect to the invariant pairing (−, −).
(ii) l(x, y)⌢′l(z, w): = p([[x, y], [z, w]]), l(x, y) ≠ l(z, w).
(iii) S1⌣′S2 : = S1⌣S2 and S1⌢′S2 : = S1⌢S2, in all other cases.
Proposition 2.4. The set Latt(𝔤) with Arnold products becomes a lattice and it is the same as the classical subspace lattice.
Proof. By the invariancy of the pairing, we have ([x, y], x) = ([x, y], y) = 0. This gives
In the following, we omit the “prime” on the Arnold products.
Remark 2.5 (Lie algebra identities versus lattice identities). We put l([x, y]): = l(x, y). Then the Arnold products are coherent with the Lie bracket, namely,
Example 2.6 (see, [1, 2]). We assume that 𝔤 : = sl(2, ℝ) generated by the standard basis (X, Y, H) satisfying the following relations:
Remark 2.7. The pairing induces a metric (−++) on (ℝ3 : x0, x1, x2). It is well known that the inside of the circle (so-called timelike subspace) is a hyperbolic plane. The altitude theorem is strictly a theorem on the hyperbolic plane because a metric is needed to define the notion of altitude.
Corollary 2.8 (see [1].)Given a line l(x, y), p([x, y]) is the pole of the line.
Figure 2 is depicting the duality defined by an ellipse.
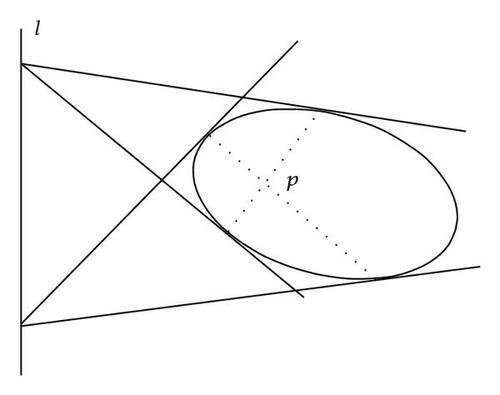
The line l is the polar line of the point p which is inside an ellipse. The line and point are connected by the tangent lines and chords of the ellipse. This figure has been drawn in a book by Kawada in [4].
We did not use Jacobi identity in this section. So we will discuss the Jacobi identity on the Lie algebra in the next section.
2.3. Jacobi Identity
Proposition 2.9. Let V be a 3D 𝕂-vector space equipped with a skew-symmetric bracket product [−, −] and a nondegenerate symmetric invariant pairing (−, −). Then the bracket satisfies the Jacobi identity.
Proof. When x, y, z ∈ V are linearly dependent, Jacobi identity holds. So we assume that x, y, z is linear independent.
Case 1. By the invariancy of the pairing, we have
Case 2. Assume that [x, [y, z]] ≠ 0. We already saw that ([[x, y], z]+[y, [x, z]], x) = 0. We show that ([[x, y], z]+[y, [x, z]], [y, z]) = 0. Since dim (V) = 3, one can put [y, z] = ax + by + cz, for some a, b, c ∈ 𝕂. Then we have
The proposition above indicates that the Jacobi identity is a priori invested in the projective plane.
2.4. Duality Principle
This mapping is called a Plücker embedding.
Proposition 2.10. The diagram below is commutative:
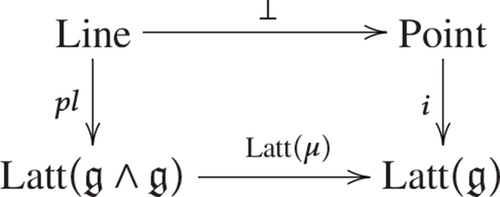 (2.22)
(2.22)Namely, the Lie algebra multiplication is equivalent to the duality principle.
3. r-Matrices
Remark 3.1. When 𝔤 = o(3, ℝ), there is no nontrivial triangular r-matrix.
Proposition 3.2. The set of points p(r) associated with nontrivial triangular r-matrices
Proof. Since dim 𝔤 = 3, one can write r = r1⋀r2 for some r1, r2 ∈ 𝔤. By the biderivation property of the Schouten-Nijenhuis bracket, we have
Lemma 3.3. The set of lines l(x, y) including the pole p([x, y]) corresponds to ℙ(r), via the Plücker embedding.
If p([x, y]) ≤ l(x, y), then the pairing ([x, y], [x, y]) vanishes, because ([x, y], [x, y]) = ([x, y], λx + μy) = 0. Hence p([x, y]) is on the quadratic curve. It is easy to check that l(x, y) is not cross over the curve. Hence the line is tangent to the curve at p([x, y]).
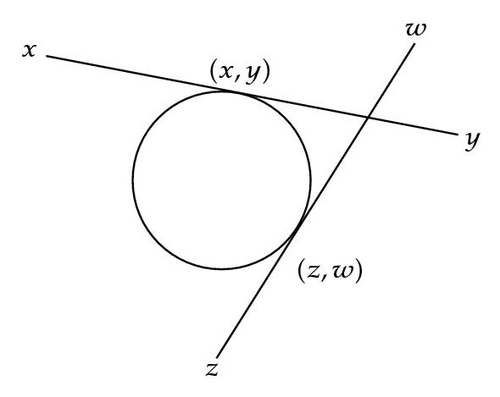
Lemma 3.4. A line is tangent to the quadratic curve if and only if the pole is on the line, and the tangent point is the pole of the line (see Figure 3).
Acknowledgment
The author would like to express his thanks to Professor Akira Yoshioka and Dr. Toshio Tomihisa for their helpful comments.
Endnotes
- 1.
The complement is not unique in general.




