Study of Possible Obstacles Preventing Obtaining a Tokomak Regime in the Egyptian Machine

2.1. Compensation of Stray Magnetic Fields

As the first step, the level of compensation of stray magnetic field with the help of permanent coils should be tested. The main sources of this field could be the toroidal field coils (due to their small misalignment) and the ohmic heating winding (because there is no iron core).

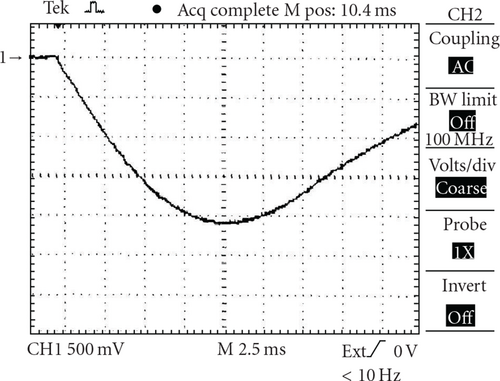
For measurements of the vertical magnetic field from the OH coil, a pick-up coil was used [1]. This coil was placed at the center of the plasma chamber. In Figure 1, one can see the wave-form of the stray magnetic field from the OH coil without compensation. The wave-form of this magnetic field with compensation is presented in Figure 2.

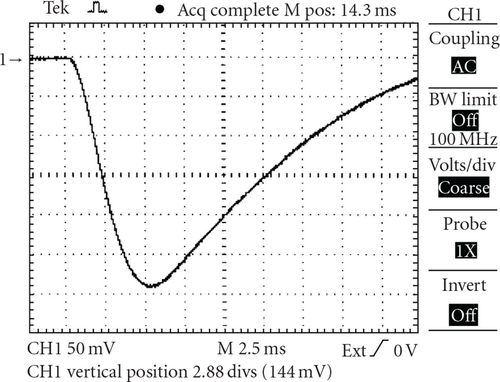
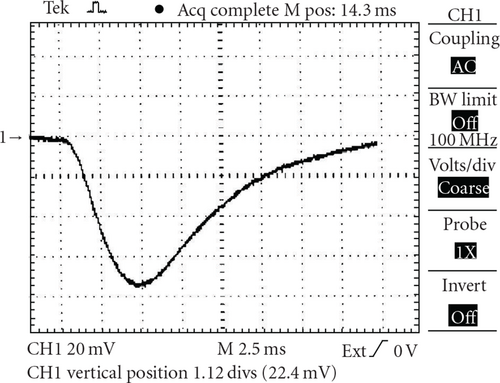
So one can see that the compensation reduces the stray magnetic field about 4.6 times. Taking into account that the sensitivity of the pick-up coil is B[T] = 0.017U[V] (where B is the magnetic field value and U is the signal value), and that in these experiments the voltage on the OH battery was 1 kV, one can find that the value of the stray magnetic field after compensation is about 1.2 × 10⁻³U_OH[kV], where U_OH is the OH battery voltage in kV.

The measurement of the vertical component of the toroidal magnetic field with the help of the same pick-up coil is practically impossible because it is very difficult to place this coil properly (see Figure 3).

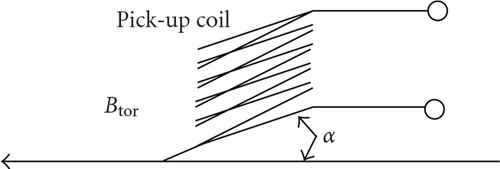
The plane of the pick-up coils must be parallel to the toroidal magnetic field B_tor. If this condition is not met, a signal will be generated in the pick-up coil, which is proportional to sin α. In practice the value of this signal is much greater than the signal from the stray magnetic field.

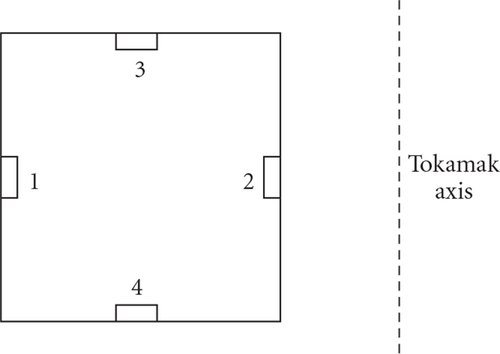
For measurements of the stray vertical field of the toroidal field coils, four (1–4) additional coils were used. These coils were placed on the bottom and top sides of the vacuum chamber as is shown in Figure 4.

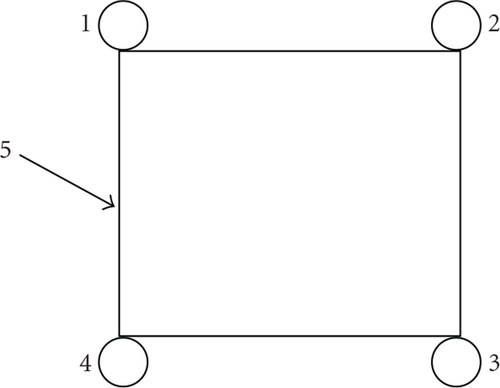
Coil 1 was connected with coil 2 in series as it can be seen in Figure 5.

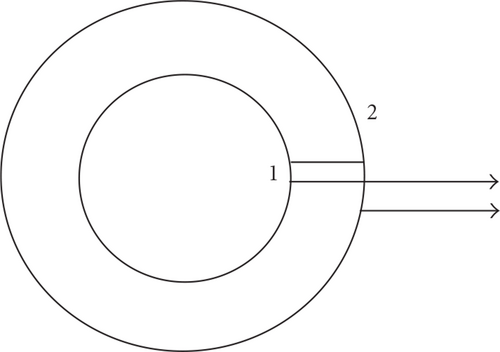
Coil 3 was connected with coil 4 in series, too. The difference between signals from loops 1 and 2 (or 3 and 4), which can be obtained after subtraction (or summation with opposite polarity) on a resistive divider, gives after integration the value of the vertical magnetic flux Ψ_1-2 or Ψ_3-4 between these two loops. Knowing their dimensions (radii) and, accordingly, the surface between them, $$, one can find the average vertical magnetic field $$. Absolute values of B_⊥ field can be determined by comparison with measurements by a calibrated pick-up coil [3]. Since the effective surface of this coil equals to πD²N (D = 1.5 cm is its diameter, N = 120: number of turns), that is, 842 cm², and surface S_1-2 equals to π(45² − 15²) = 5655 cm², so with using the same integrator their sensitivities will differ by a factor 6.7 (loops are more sensitive). So the sensitivity of loops 1-2 is equal to 0.114 T/V. The waveform of the vertical component of the toroidal magnetic field is given in Figure 6.

In a similar manner, one can obtain estimations of the average horizontal magnetic field which determines the equilibrium in vertical direction. For this purpose one should combine the signals of loops 1 and 3 (or 2 and 4), but their effective surface in this case will be S_1-3 = 2πR_1,3Δz, where Δz is vertical distance between loops 1 and 3 (38 cm), that is, S₁₋₃ = 10744 cm².

The signal from 1 + 2 coils is given in Figure 6. Taking into account the radii of the inner and outer coils (15 and 45 cm), we can estimate the value of the stray vertical fields from toroidal coil and ohmic heating coil as being not higher than 5 Gs. So we can conclude that the measured values of stray magnetic fields cannot prevent the discharge breakdown and limit its duration.

2.2. Plasma Equilibrium

Because Mirnov probes and these loops were not calibrated, we could make only some estimations of the plasma equilibrium. If the center of the plasma current coincides with the center of the chamber (i.e., at equal distances from both probes) these signals must be equal (in cylindrical approximation). In a torus these signals will differ due the toroidicity by the ratio (R + b )/(R − b). Due to the lack of equilibrium, that is, displacement Δ of plasma current relative to chamber axis, the signal in one of Mirnov probes (outer) will increase ~J_p/(b − Δ) ((J_p/b)(1 + Δ/b) for small displacements). Analogously, the signal from inner probe will decrease as (J_p/b)(1 − Δ/b) and their difference will be ~2J_pΔ/b². So if we adjust the signals from these two Mirnov probes in accordance with their toroidicity and then subtract these signals, we will obtain the signal proportional to displacement of the plasma current. But as one can see from these signals (Figure 8) their shapes are similar and repeat practically the shape of plasma current signal.

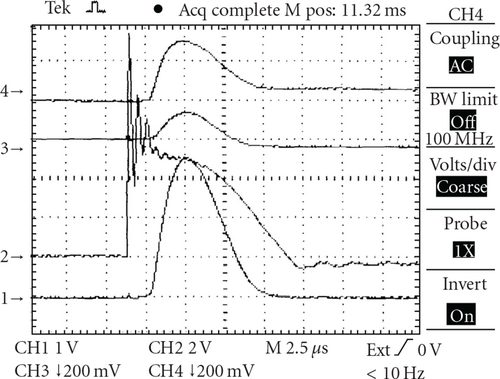
The relative difference between these signals (or signal after their normalization and subtraction—Figure 9) is not more than 0.125 which corresponds to displacement of not more than 0.06 b, that is, ~0.5 cm.

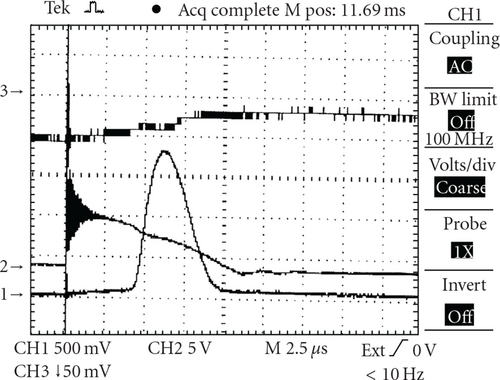
So we can conclude that the plasma equilibrium in these discharges is good enough and in any case could not be the reason for their short duration or small plasma current value.

2.3. MHD Instabilities

For B_t = 0.4 T (corresponding to U_tor = 1 kV), plasma current J_p = 5 kA, and a = 7 cm, the q value equals to 1.7 · 10³ · 0.4 · 49/5 · 10³ = 6.7. This value is large enough because most dangerous MHD modes have q values of 2 and 3. So MHD instabilities most likely cannot be responsible for the short duration and the small amplitude of the plasma current.

2.4. Influence of Impurities

For a plasma current J_p = 5 kA and a loop voltage 25 V and assuming a = 7 cm, we obtain $$. This value is very close to the so-called “radiation limit” which was observed in first tokamaks and is associated with high level of impurities.