We describe our recent results on the resonant perturbation theory of decoherence and relaxation for quantum systems with many qubits. The approach represents a rigorous analysis of the phenomenon of decoherence and relaxation for general N-level systems coupled to reservoirs of bosonic fields. We derive a representation of the reduced dynamics valid for all times t ≥ 0 and for small but fixed interaction strength. Our approach does not involve master equation approximations and applies to a wide variety of systems which are not explicitly solvable.

1. Introduction

Quantum computers (QCs) with large numbers of quantum bits (qubits) promise to solve important problems such as factorization of larger integer numbers, searching large unsorted databases, and simulations of physical processes exponentially faster than digital computers. Recently, many efforts were made for designing scalable (in the number of qubits) QC architectures based on solid-state implementations. One of the most promising designs of a solid-state QC is based on superconducting devices with Josephson junctions and solid-state quantum interference devices (SQUIDs) serving as qubits (effective spins), which operate in the quantum regime: ℏω > >k_BT, where T is the temperature and ω is the qubit transition frequency. This condition is widely used in superconducting quantum computation and quantum measurement, when T~ 10–20 mK and ℏω~ 100–150 mK (in temperature units) [1–8] (see also references therein). The main advantages of a QC with superconducting qubits are: (i) the two basic states of a qubit are represented by the states of a superconducting charge or current in the macroscopic (several μm size) device. The relatively large scale of this device facilitates the manufacturing, and potential controlling and measuring of the states of qubits. (ii) The states of charge- and current-based qubits can be measured using rapidly developing technologies, such as a single electron transistors, effective resonant oscillators and microcavities with RF amplifiers, and quantum tunneling effects. (iii) The quantum logic operations can be implemented exclusively by switching locally on and off voltages on controlling microcontacts and magnetic fluxes. (iv) The devices based on superconducting qubits can potentially achieve large quantum dephasing and relaxation times of milliseconds and more at low temperatures, allowing quantum coherent computation for long enough times. In spite of significant progress, current devices with superconducting qubits only have one or two qubits operating with low fidelity even for simplest operations.

One of the main problems which must be resolved in order to build a scalable QC is to develop novel approaches for suppression of unwanted effects such as decoherence and noise. This also requires to develop rigorous mathematical tools for analyzing the dynamics of decoherence, entanglement, and thermalization in order to control the quantum protocols with needed fidelity. These theoretical approaches must work for long enough times and be applicable to both solvable and not explicitly solvable (nonintegrable) systems.

Here we present a review of our results [9–11] on the rigorous analysis of the phenomenon of decoherence and relaxation for general N-level systems coupled to reservoirs. The latter are described by the bosonic fields. We suggest a new approach which applies to a wide variety of systems which are not explicitly solvable. We analyze in detail the dynamics of an N-qubit quantum register collectively coupled to a thermal environment. Each spin experiences the same environment interaction, consisting of an energy conserving and an energy exchange part. We find the decay rates of the reduced density matrix elements in the energy basis. We show that the fastest decay rates of off-diagonal matrix elements induced by the energy conserving interaction are of order N², while the one induced by the energy exchange interaction is of the order N only. Moreover, the diagonal matrix elements approach their limiting values at a rate independent of N. Our method is based on a dynamical quantum resonance theory valid for small, fixed values of the couplings, and uniformly in time for t ≥ 0. We do not make Markov-, Born- or weak coupling (van Hove) approximations.

2. Presentation of Results

We consider an N-level quantum system S interacting with a heat bath R. The former is described by a Hilbert space 𝔥_s = ℂ^N and a Hamiltonian

(2.1)

The environment R is modelled by a bosonic thermal reservoir with Hamiltonian

(2.2)

acting on the reservoir Hilbert space 𝔥_R, and where a^*(k) and a(k) are the usual bosonic creation and annihilation operators satisfying the canonical commutation relations [a(k), a^*(l)] = δ(k − l). It is understood that we consider R in the thermodynamic limit of infinite volume (ℝ³) and fixed temperature T = 1/β > 0 (in a phase without condensate). Given a form factor f(k), a square integrable function of k ∈ ℝ³ (momentum representation), the smoothed-out creation and annihilation operators are defined as

and

, respectively, and the hermitian field operator is

(2.3)

The total Hamiltonian, acting on 𝔥_S ⊗ 𝔥_R, has the form

(2.4)

where λ is a coupling constant and v is an interaction operator linear in field operators. For simplicity of exposition, we consider here initial states where S and R are not entangled, and where R is in thermal equilibrium. (Our method applies also to initially entangled states, and arbitrary initial states of R normal w.r.t. the equilibrium state; see [10]). The initial density matrix is thus

(2.5)

where

is any state of S and ρ_R,β is the equilibrium state of R at temperature 1/β.

Let A be an arbitrary observable of the system (an operator on the system Hilbert space 𝔥_S) and set

(2.6)

where ρ_t is the density matrix of S + R at time t and

(2.7)

is the reduced density matrix of S. In our approach, the dynamics of the reduced density matrix

is expressed in terms of the resonance structure of the system. Under the noninteracting dynamics (λ = 0), the evolution of the reduced density matrix elements of S, expressed in the energy basis

of H_S, is given by

(2.8)

where e_lk = E_l − E_k. As the interaction with the reservoir is turned on, the dynamics (2.8) undergoes two qualitative changes.

(1)
The “Bohr frequencies”
(2.9)
in the exponent of (2.8) become complex, e ↦ ɛ_e. It can be shown generally that the resonance energies ɛ_e have nonnegative imaginary parts, Im ɛ_e ≥ 0. If Im ɛ_e > 0, then the corresponding dynamical process is irreversible.
(2)
The matrix elements do not evolve independently any more. Indeed, the effective energy of S is changed due to the interaction with the reservoirs, leading to a dynamics that does not leave eigenstates of H_S invariant. (However, to lowest order in the interaction, the eigenspaces of H_S are left invariant and therefore matrix elements with (m, n) belonging to a fixed energy difference E_m − E_n will evolve in a coupled manner.)

Our goal is to derive these two effects from the microscopic (hamiltonian) model and to quantify them. Our analysis yields the thermalization and decoherence times of quantum registers.

2.1. Evolution of Reduced Dynamics of an N-Level System

Let A ∈ ℬ(𝔥_S) be an observable of the system S. We show in [9, 10] that the ergodic averages

(2.10)

exist, that is, 〈A〉_t converges in the ergodic sense as t → ∞. Furthermore, we show that for any t ≥ 0 and for any 0 < ω^′ < 2π/β,

(2.11)

where the complex numbers ɛ are the eigenvalues of a certain explicitly given operator K(ω′), lying in the strip {z ∈ ℂ | 0 ≤ Im z < ω′/2}. They have the expansions

(2.12)

where e ∈ spec(H_S ⊗ 1_S − 1_S ⊗ H_S) = spec(H_S) − spec(H_S) and

are the eigenvalues of a matrix Λ_e, called a level-shift operator, acting on the eigenspace of H_S ⊗ 1_S − 1_S ⊗ H_S corresponding to the eigenvalue e (which is a subspace of 𝔥_S ⊗ 𝔥_S). The R_ɛ(A) in (2.11) are linear functionals of A and are given in terms of the initial state, ρ₀, and certain operators depending on the Hamiltonian H. They have the expansion

(2.13)

where I_e is the collection of all pairs of indices such that e = E_m − E_n, with E_k being the eigenvalues of H_S. Here, A_m,n is the (m, n)-matrix element of the observable A in the energy basis of H_S, and ϰ_m,n are coefficients depending on the initial state of the system (and on e, but not on A nor on λ).

2.1.1. Discussion

(i)
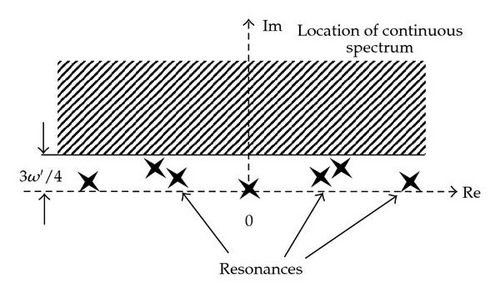
In the absence of interaction (λ = 0), we have ɛ = e ∈ ℝ; see (2.12). Depending on the interaction, each resonance energy ɛ may migrate into the upper complex plane, or it may stay on the real axis, as λ ≠ 0.
(ii)
The averages 〈A〉_t approach their ergodic means 〈〈A〉〉_∞ if and only if Im ɛ > 0 for all ɛ ≠ 0. In this case, the convergence takes place on the time scale [Im ɛ] ⁻¹. Otherwise; 〈A〉_t oscillates. A sufficient condition for decay is that (and λ small, see (2.12)).
(iii)
The error term in (2.11) is small in λ, uniformly in t ≥ 0, and it decays in time quicker than any of the main terms in the sum on the r.h.s.: indeed, Im ɛ = O(λ²) while ω^′ − O(λ) > ω^′/2 independent of small values of λ. However, this means that we are in the regime λ² ≪ ω^′ < 2π/β (see before (2.11)), which implies that λ² must be much smaller than the temperature T = 1/β. Using a more refined analysis, one can get rid of this condition; see also remarks on page 376 of [10].
(iv)
Relation (2.13) shows that to lowest order in the perturbation, the group of (energy basis) matrix elements of any observable A corresponding to a fixed energy difference E_m − E_n evolve jointly, while those of different such groups evolve independently.

It is well known that there are two kinds of processes which drive decay (or irreversibility) of S: energy-exchange processes characterized by [v, H_S] ≠ 0 and energy preserving ones where [v, H_S] = 0. The former are induced by interactions having nonvanishing probabilities for processes of absorption and emission of field quanta with energies corresponding to the Bohr frequencies of S and thus typically inducing thermalization of S. Energy preserving interactions suppress such processes, allowing only for a phase change of the system during the evolution (“phase damping”, [12–18]).

To our knowledge, energy-exchange systems have so far been treated using Born and Markov master equation approximations (Lindblad form of dynamics) or they have been studied numerically, while for energy conserving systems, one often can find an exact solution. The present representation (2.11) gives a detailed picture of the dynamics of averages of observables for interactions with and without energy exchange. The resonance energies ɛ and the functionals R_ɛ can be calculated for concrete models, as illustrated in the next section. We mention that the resonance dynamics representation can be used to study the dynamics of entanglement of qubits coupled to local and collective reservoirs, see [19].

The dynamical resonance method can be generalized to time-dependent Hamiltonians. See [20, 21] for time-periodic Hamiltonians.

2.1.2. Contrast with Weak Coupling Approximation

Our representation (2.11) of the true dynamics of S relies only on the smallness of the coupling parameter λ, and no approximation is made. In the absence of an exact solution, it is common to make a weak coupling Lindblad master equation approximation of the dynamics, in which the reduced density matrix evolves according to , where ℒ is the Lindblad generator, [22–24]. This approximation can lead to results that differ qualitatively from the true behaviour. For instance, the Lindblad master equation predicts that the system S approaches its Gibbs state at the temperature of the reservoir in the limit of large times. However, it is clear that in reality, the coupled system S + R will approach equilibrium, and hence the asymptotic state of S alone, being the reduction of the coupled equilibrium state, is the Gibbs state of S only to first approximation in the coupling (see also illustration below, and [9, 10]). In particular, the system′s asymptotic density matrix is not diagonal in the original energy basis, but it has off-diagonal matrix elements of O(λ²). Features of this kind cannot be captured by the Lindblad approximation, but are captured in our approach.

It has been shown (see, e.g., [23–26]) that the weak coupling limit dynamics generated by the Lindblad operator is obtained in the regime λ → 0, t → ∞, with λ²t fixed. One of the strengths of our approach is that we do not impose any relation between λ and t, and our results are valid for all times t ≥ 0, provided λ is small. It has been observed [25, 26] that for certain systems of the type S + R, the second-order contribution of the exponents in (2.12) correspond to eigenvalues of the Lindblad generator. Our resonance method gives the true exponents, that is, we do not lose the contributions of any order in the interaction. If the energy spectrum of H_S is degenerate, it happens that the second-order contributions to vanish. This corresponds to a Lindblad generator having several real eigenvalues. In this situation, the correct dynamics (approach to a final state) can be captured only by taking into account higher-order contributions to the exponents ; see [27]. To our knowledge, so far this can only be done with the method presented in this paper, and is beyond the reach of the weak coupling method.

2.1.3. Illustration: Single Qubit

Consider S to be a single spin 1/2 with energy gap Δ = E₂ − E₁ > 0. S is coupled to the heat bath R via the operator

(2.14)

where ϕ(g) is the Bose field operator (2.3), smeared out with a coupling function (form factor) g(k), k ∈ ℝ³, and the 2 × 2 coupling matrix (representing the coupling operator in the energy eigenbasis) is hermitian. The operator (2.14)—or a sum of such terms, for which our technique works equally well—is the most general coupling which is linear in field operators. We refer to [10] for a discussion of the link between (2.14) and the spin-boson model. We take S initially in a coherent superposition in the energy basis,

(2.15)

In [10] we derive from representation (2.11) the following expressions for the dynamics of matrix elements, for all t ≥ 0:

(2.16)

(2.17)

where the resonance energies ɛ are given by

(2.18)

with

(2.19)

The remainder terms in (2.17), (2.17) satisfy |R_m,n(λ, t)| ≤ Cλ², uniformly in t ≥ 0, and they can be decomposed into a sum of a constant and a decaying part,

(2.20)

where |R′_m,n(λ, t)| = O(λ²e^−γt), with γ = min {Im ɛ₀, Im ɛ_±Δ}. These relations show the following.

(i)
To second order in λ, convergence of the populations to the equilibrium values (Gibbs law), and decoherence occur exponentially fast, with rates τ_T = [Im ɛ₀(λ)] ⁻¹ and τ_D = [Im ɛ_Δ(λ)] ⁻¹, respectively. (If either of these imaginary parts vanishes then the corresponding process does not take place, of course.) In particular, coherence of the initial state stays preserved on time scales of the order λ⁻²[|c|²ξ(Δ)+(b − a) ²ξ(0)] ⁻¹; compare for example (2.18).
(ii)
The final density matrix of the spin is not the Gibbs state of the qubit, and it is not diagonal in the energy basis. The deviation of the final state from the Gibbs state is given by lim _t→∞R_m,n(λ, t) = O(λ²). This is clear heuristically too, since typically the entire system S + R approaches its joint equilibrium in which S and R are entangled. The reduction of this state to S is the Gibbs state of S modulo O(λ²) terms representing a shift in the effective energy of S due to the interaction with the bath. In this sense, coherence in the energy basis of S is created by thermalization. We have quantified this in [10, Theorem 3.3].
(iii)
In a markovian master equation approach, the above phenomenon (i.e., variations of O(λ²) in the time-asymptotic limit) cannot be detected. Indeed in that approach one would conclude that S approaches its Gibbs state as t → ∞.

2.2. Evolution of Reduced Dynamics of an N-Level System

In the sequel, we analyze in more detail the evolution of a qubit register of size N. The Hamiltonian is

(2.21)

where J_ij are pair interaction constants and B_j is the value of a magnetic field at the location of spin j. The Pauli spin operator is

(2.22)

and

is the matrix S^z acting on the jth spin only.

We consider a collective coupling between the register S and the reservoir R: the distance between the N qubits is much smaller than the correlation length of the reservoir and as a consequence, each qubit feels the same interaction with the reservoir. The corresponding interaction operator is (compare with (2.4))

(2.23)

Here g₁ and g₂ are form factors and the coupling constants λ₁ and λ₂ measure the strengths of the energy conserving (position-position) coupling, and the energy exchange (spin flip) coupling, respectively. Spin-flips are implemented by the

in (2.23), representing the Pauli matrix

(2.24)

acting on the jth spin. The total Hamiltonian takes the form (2.4) with λv replaced by (2.23). It is convenient to represent

as a matrix in the energy basis, consisting of eigenvectors

of H_S. These are vectors in

indexed by spin configurations

(2.25)

where

(2.26)

so that

(2.27)

We denote the reduced density matrix elements as

(2.28)

The Bohr frequencies (2.9) are now

(2.29)

and they become complex resonance energies ɛ_e = ɛ_e(λ₁, λ₂) ∈ ℂ under perturbation.

Assumption of Nonoverlapping Resonances The Bohr frequencies (2.29) represent “unperturbed” energy levels and we follow their motion under perturbation (λ₁, λ₂). In this work, we consider the regime of nonoverlapping resonances, meaning that the interaction is small relative to the spacing of the Bohr frequencies.

We show in [10, Theorem 2.1], that for all t ≥ 0,

(2.30)

This result is obtained by specializing (2.11) to the specific system at hand and considering observables

. In (2.30), we have in accordance with (2.10),

. The coefficients w are overlaps of resonance eigenstates which vanish unless

(see point (2) after (2.9)). They represent the dominant contribution to the functionals R_ɛ in (2.11); see also (2.13). The ɛ_e have the expansion

(2.31)

where the label s = 1, …, ν(e) indexes the splitting of the eigenvalue e into ν(e) distinct resonance energies. The lowest order corrections

satisfy

(2.32)

They are the (complex) eigenvalues of an operator Λ_e, called the level shift operator associated to e. This operator acts on the eigenspace of L_S associated to the eigenvalue e (a subspace of the qubit register Hilbert space; see [10, 11] for the formal definition of Λ_e). It governs the lowest order shift of eigenvalues under perturbation. One can see by direct calculation that

2.2.1. Discussion

(i)
To lowest order in the perturbation, the group of reduced density matrix elements associated to a fixed evolve in a coupled way, while groups of matrix elements associated to different e evolve independently.
(ii)
The density matrix elements of a given group mix and evolve in time according to the weight functions w and the exponentials . In the absence of interaction (λ₁ = λ₂ = 0), all the are real. As the interaction is switched on, the typically migrate into the upper complex plane, but they may stay on the real line (due to some symmetry or due to an “inefficient coupling”).
(iii)
The matrix elements of a group e approach their ergodic means if and only if all the nonzero have strictly positive imaginary part. In this case, the convergence takes place on a time scale of the order 1/γ_e, where
(2.33)
is the decay rate of the group associated to e. If an stays real, then the matrix elements of the corresponding group oscillate in time. A sufficient condition for decay of the group associated to e is γ_e > 0, that is, for all s, and λ₁, λ₂ small.

2.2.2. Decoherence Rates

We illustrate our results on decoherence rates for a qubit register with J_ij = 0 (the general case is treated in [11]). We consider generic magnetic fields defined as follows. For n_j ∈ {0, ±1, ±2}, j = 1, …, N, we have

(2.34)

Condition (2.34) is satisfied generically in the sense that it does not hold only for very special choices of B_j (one such special choice is B_j = constant). For instance, if the B_j are chosen to be independent, and uniformly random from an interval [B_min, B_max], then (2.34) is satisfied with probability one. We show in [11, Theorem 2.3], that the decoherence rates (2.33) are given by

(2.35)

Here, y₁ is contributions coming from the energy conserving interaction; y₀ and y₂ are due to the spin flip interaction. The term y₁₂ is due to both interactions and is of

. We give explicit expressions for y₀, y₁, y₂, and y₁₂ in [11, Section 2]. For the present purpose, we limit ourselves to discussing the properties of the latter quantities.

(i)
Properties of y₁(e): y₁(e) vanishes if either e is such that or the infrared behaviour of the coupling function g₁ is too regular (in three dimensions g₁∝|k|^p with p > −1/2). Otherwise, y₁(e) > 0. Moreover, y₁(e) is proportional to the temperature T.
(ii)
Properties of y₂(e): y₂(e) > 0 if g₂(2B_j, Σ) ≠ 0 for all B_j (form factor g₂(k) = g₂(|k | , Σ) in spherical coordinates). For low temperatures, T, y₂(e) ∝ T, for high temperatures y₂(e) approaches a constant.
(iii)
Properties of y₁₂(e): if either of λ₁, λ₂ or e₀ vanish, or if g₁ is infrared regular as mentioned above, then y₁₂(e) = 0. Otherwise, y₁₂(e) > 0, in which case y₁₂(e) approaches constant values for both T → 0, ∞.
(iv)
Full decoherence: if γ_e > 0 for all e ≠ 0, then all off-diagonal matrix elements approach their limiting values exponentially fast. In this case, we say that full decoherence occurs. It follows from the above points that we have full decoherence if λ₂ ≠ 0 and g₂(2B_j, Σ) ≠ 0 for all j, and provided λ₁, λ₂ are small enough (so that the remainder term in (2.35) is small). Note that if λ₂ = 0, then matrix elements associated to energy differences e such that e₀ = 0 will not decay on the time scale given by the second order in the perturbation (). We point out that generically, S + R will reach a joint equilibrium as t → ∞, which means that the final reduced density matrix of S is its Gibbs state modulo a peturbation of the order of the interaction between S and R; see [9, 10]. Hence generically, the density matrix of S does not become diagonal in the energy basis as t → ∞.
(v)
Properties of y₀: y₀ depends on the energy exchange interaction only. This reflects the fact that for a purely energy conserving interaction, the populations are conserved [9, 10, 17]. If g₂(2B_j, Σ) ≠ 0 for all j, then y₀ > 0 (this is sometimes called the “Fermi Golden Rule Condition”). For small temperatures T, y₀ ∝ T, while y₀ approaches a finite limit as T → ∞.

In terms of complexity analysis, it is important to discuss the dependence of γ_e on the register size N.

(i)
We show in [11] that y₀ is independent of N. This means that the thermalization time, or relaxation time of the diagonal matrix elements (corresponding to e = 0), is O(1) in N.
(ii)
To determine the order of magnitude of the decay rates of the off-diagonal density matrix elements (corresponding to e ≠ 0) relative to the register size N, we assume the magnetic field to have a certain distribution denoted by 〈·〉. We show in [11] that
(2.36)
where C_B and c_B = c_B(λ₁, λ₂) are positive constants (independent of N), with . Here, N₀(e) is the number of indices j such that σ_j = τ_j for each s.t. , and
(2.37)
is the Hamming distance between the spin configurations and (which depends on e only).
(iii)
Consider e ≠ 0. It follows from (2.35)–(2.37) that for purely energy conserving interactions (λ₂ = 0), , which can be as large as . On the other hand, for purely energy exchanging interactions (λ₁ = 0), we have , which cannot exceed . If both interactions are acting, then we have the additional term 〈y₁₂〉, which is of order . This shows the following: The fastest decay rate of reduced off-diagonal density matrix elements due to the energy conserving interaction alone is of order , while the fastest decay rate due to the energy exchange interaction alone is of the order . Moreover, the decay of the diagonal matrix elements is of order , that is, independent of N.

Remark 2.2.2 s. (1) For λ₂ = 0, the model can be solved explicitly [17], and one shows that the fastest decaying matrix elements have decay rate proportional to . Furthermore, the model with a noncollective, energy-conserving interaction, where each qubit is coupled to an independent reservoir, can also be solved explicitly [17]. The fastest decay rate in this case is shown to be proportional to .

(2) As mentioned at the beginning of this section, we take the coupling constants λ₁, λ₂ so small that the resonances do not overlap. Consequently, and are bounded above by a constant proportional to the gradient of the magnetic field in the present situation; see also [11]. Thus the decay rates γ_e do not increase indefinitely with increasing N in the regime considered here. Rather, γ_e are attenuated by small coupling constants for large N. They are of the order γ_e ~ Δ. We have shown that modulo an overall, common (N-dependent) prefactor, the decay rates originating from the energy conserving and exchanging interactions differ by a factor N.

(3) Collective decoherence has been studied extensively in the literature. Among the many theoretical, numerical, and experimental works, we mention here only [12, 14, 17, 28, 29], which are closest to the present work. We are not aware of any prior work giving explicit decoherence rates of a register for not explicitly solvable models, and without making master equation technique approximations.

3. Resonance Representation of Reduced Dynamics

The goal of this section is to give a precise statement of the core representation (2.11), and to outline the main ideas behind the proof of it.

The N-level system is coupled to the reservoir (see also (2.1), (2.2)) through the operator

(3.1)

where each G_r is a hermitian N × N matrix, the g_r(k) are form factors, and the λ_r ∈ ℝ are coupling constants. Fix any phase χ ∈ ℝ and define

(3.2)

where u ∈ ℝ and σ ∈ S². The phase χ is a parameter which can be chosen appropriately as to satisfy the following condition.

(A)
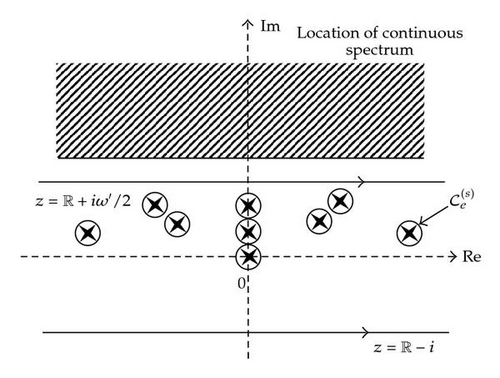
The map ω ↦ g_r,β(u + ω, σ) has an analytic extension to a complex neighbourhood {|z | < ω′} of the origin, as a map from ℂ to L²(ℝ³, d³k).

Examples of g satisfying (A) are given by , where p = −1/2 + n, n = 0,1, …, m = 1,2, and .

This condition ensures that the technically simplest version of the dynamical resonance theory, based on complex spectral translations, can be implemented. The technical simplicity comes at a price: on one hand, it limits the class of admissible functions g(k), which have to behave appropriately in the infrared regime so that the parts of (3.2) fit nicely together at u = 0, to allow for an analytic continuation. On the other hand, the square root in (3.2) must be analytic as well, which implies the condition ω^′ < 2π/β.

It is convenient to introduce the doubled Hilbert space ℋ_S = 𝔥_S ⊗ 𝔥_S, whose normalized vectors accommodate any state on the system S (pure or mixed). The trace state, or infinite temperature state, is represented by the vector

(3.3)

via

(3.4)

Here φ_j are the orthonormal eigenvectors of H_S. This is just the Gelfand-Naimark-Segal construction for the trace state. Similarly, let ℋ_R and Ω_R,β be the Hilbert space and the vector representing the equilibrium state of the reservoirs at inverse temperature β. In the Araki-Woods representation of the field, we have ℋ_R = ℱ ⊗ ℱ, where ℱ is the bosonic Fock space over the one-particle space L²(ℝ³, d³k) and Ω_R,β = Ω ⊗ Ω, with Ω being the Fock vacuum of ℱ (see also [10, 11] for more detail). Let ψ₀ ⊗ Ω_R,β be the vector in ℋ_S ⊗ ℋ_R representing the density matrix at time t = 0. It is not difficult to construct the unique operator in B ∈ 1_S ⊗ 𝔥_S satisfying

(3.5)

(See also [10] for concrete examples.) We define the reference vector

(3.6)

and set

(3.7)

Theorem 3.1 (Dynamical resonance theory [9–11]). Assume condition (A) with a fixed ω^′ satisfying 0 < ω^′ < 2π/β. There is a constant c₀ s.t.; if λ ≤ c₀/β, then the limit 〈〈A〉〉_∞, (2.10), exists for all observables A ∈ ℬ(𝔥_S). Moreover, for all such A and for all t ≥ 0, we have

(3.8)

The

are given by (2.12), 1 ≤ ν(e) ≤ mult(e) counts the splitting of the eigenvalue e into distinct resonance energies

, and the

are (nonorthogonal) finite-rank projections.

This result is the basis for a detailed analysis of the reduced dynamics of concrete systems, like the N-qubit register introduced in Section 2.2. We obtain (2.30) (in particular, the overlap functions w) from (3.8) by analyzing the projections in more detail. Let us explain how to link the overlap to its initial value for a nondegenerate Bohr energy e, and where A = |φ_n〉〈φ_m|. (The latter observables used in (2.11) give the matrix elements of the reduced density matrix in the energy basis.)

The

is the spectral (Riesz) projection of an operator K_λ associated with the eigenvalue

; see (3.19) (In reality, we consider a spectral deformation K_λ(ω), where ω is a complex parameter. This is a technical trick to perform our analysis. Physical quantities do not depend on ω and therefore, we do not display this parameter here). If a Bohr energy e, (2.9), is simple, then there is a single resonance energy ɛ_e bifurcating out of e, as λ ≠ 0. In this case, the projection

has rank one,

, where χ_e and

are eigenvectors of K_λ and its adjoint, with eigenvalue ɛ_e and its complex conjugate, respectively, and

. From perturbation theory, we obtain

, where H_Sφ_j = E_jφ_j and E_k − E_l = e. The overlap in the sum of (3.8) becomes

(3.9)

The choice A = |φ_n〉〈φ_m| in (2.6) gives

, the reduced density matrix element. With this choice of A, the main term in (3.9) becomes (see also (3.3))

(3.10)

In the second-last step, we commute B to the right through |φ_n〉〈φ_m | ⊗ 1_S, since B belongs to the commutant of the algebra of observables of S. In the last step, we use BΩ_S = ψ₀.

Combining (3.9) and (3.10) with Theorem 3.1 we obtain, in case e = E_m − E_n is a simple eigenvalue,

(3.11)

This explains the form (2.30) for a simple Bohr energy e. The case of degenerate e (i.e., where several different pairs of indices k, l satisfy E_k − E_l = e) is analyzed along the same lines; see [11] for details.

3.1. Mechanism of Dynamical Resonance Theory, Outline of Proof of Theorem 3.1

Consider any observable A ∈ B(𝔥_S). We have

(3.12)

In the last step, we pass to the representation Hilbert space of the system (the GNS Hilbert space), where the initial density matrix is represented by the vector ψ₀ (in particular, the Hilbert space of the small system becomes 𝔥_S ⊗ 𝔥_S); see also before (3.3), (3.4). As mentioned above, in this review we consider initial states where S and R are not entangled. The initial state is represented by the product vector ψ₀ = Ω_S ⊗ Ω_R,β, where Ω_S is the trace state of S, (3.4), 〈Ω_S, (A ⊗ 1_S)Ω_S〉 = (1/N)Tr (A), and where Ω_R,β is the equilibrium state of R at a fixed inverse temperature 0 < β < ∞. The dynamics is implemented by the group of automorphisms

. The self-adjoint generator L_λ is called the Liouville operator. It is of the form L_λ = L₀ + λW, where L₀ = L_S + L_R represents the uncoupled Liouville operator, and λW is the interaction (3.1) represented in the GNS Hilbert space. We refer to [10, 11] for the specific form of W.

We borrow a trick from the analysis of open systems far from equilibrium: there is a (nonself-adjoint) generator K_λ s.t.

(3.13)

K_λ can be constructed in a standard way, given L_λ and the reference vector ψ₀. K_λ is of the form K_λ = L₀ + λI, where the interaction term undergoes a certain modification (W → I); see for example [10]. As a consequence, formally, we may replace the propagators in (3.12) by those involving K. The resulting propagator which is directly applied to ψ₀ will then just disappear due to the invariance of ψ₀. One can carry out this procedure in a rigorous manner, obtaining the following resolvent representation [10]

(3.14)

where K_λ(ω) = L₀(ω) + λI(ω), I is representing the interaction, and ω ↦ K_λ(ω) is a spectral deformation (translation) of K_λ. The latter is constructed as follows. There is a deformation transformation U(ω) = e^−iωD, where D is the (explicit) self-adjoint generator of translations [10, 11, 30] transforming the operator K_λ as

(3.15)

Here, N = N₁ ⊗ 1 + 1 ⊗ N₁ is the total number operator of a product of two bosonic Fock spaces ℱ ⊗ ℱ (the Gelfand-Naimark-Segal Hilbert space of the reservoir), and where N₁ is the usual number operator on ℱ. N has spectrum ℕ ∪ {0}, where 0 is a simple eigenvalue (with vacuum eigenvector Ω_R,β = Ω ⊗ Ω). For real values of ω, U(ω) is a group of unitaries. The spectrum of K_λ(ω) depends on Im ω and moves according to the value of Im ω, whence the name “spectral deformation”. Even though U(ω) becomes unbounded for complex ω, the r.h.s. of (3.15) is a well-defined closed operator on a dense domain, analytic in ω at zero. Analyticity is used in the derivation of (3.14) and this is where the analyticity condition (A) after (3.2) comes into play. The operator I(ω) is infinitesimally small with respect to the number operator N. Hence we use perturbation theory in λ to examine the spectrum of K_λ(ω).

The point of the spectral deformation is that the (important part of the) spectrum of K_λ(ω) is much easier to analyze than that of K_λ, because the deformation uncovers the resonances of K_λ. We have (see Figure 1)

(3.16)

because K₀(ω) = L₀ + ωN, L₀ and N commute, and the eigenvectors of L₀ = L_S + L_R are φ_i ⊗ φ_j ⊗ Ω_R,β. Here, we have H_Sφ_j = E_jφ_j. The continuous spectrum is bounded away from the isolated eigenvalues by a gap of size Im ω. For values of the coupling parameter λ small compared to Im ω, we can follow the displacements of the eigenvalues by using analytic perturbation theory. (Note that for Im ω = 0, the eigenvalues are imbedded into the continuous spectrum, and analytic perturbation theory is not valid! The spectral deformation is indeed very useful!)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Spectrum of K₀(ω).

Theorem 3.2 (see [10] and Figure 2.)Fix Im ω s.t. 0 < Im ω < ω^′ (where ω^′ is as in Condition (A)). There is a constant c₀ > 0 s.t. if |λ | ≤ c₀/β then, for all ω with Im ω > 7ω^′/8, the spectrum of K_λ(ω) in the complex half-plane {Im z < ω^′/2} is independent of ω and consists purely of the distinct eigenvalues

(3.17)

where 1 ≤ ν(e) ≤ mult(e) counts the splitting of the eigenvalue e. Moreover,

(3.18)

for all s, and we have

. Also, the continuous spectrum of K_λ(ω) lies in the region {Im z ≥ 3ω^′/4}.

Next we separate the contributions to the path integral in (3.14) coming from the singularities at the resonance energies and from the continuous spectrum. We deform the path of integration z = ℝ − i into the line z = ℝ + iω^′/2, thereby picking up the residues of poles of the integrand at

(all e, s). Let

be a small circle around

, not enclosing or touching any other spectrum of K_λ(ω). We introduce the generally nonorthogonal Riesz spectral projections

(3.19)

It follows from (3.14) that

(3.20)

Note that the imaginary parts of all resonance energies

are smaller than ω^′/2, so that the remainder term in (3.20) is not only small in λ, but it also decays faster than all of the terms in the sum. (See also Figure 3.) We point out also that instead of deforming the path integration contour as explained before (3.19), we could choose z = ℝ + i[ω^′ − O(λ)], hence transforming the error term in (3.20) into the one given in (3.8).

Finally, we notice that all terms in (3.20) with

will vanish in the ergodic mean limit, so

(3.21)

We now see that the linear functionals (2.13) are represented as

(3.22)

This concludes the outline of the proof of Theorem 3.1.

Acknowledgments

This work was carried out under the auspices of the National Nuclear Security Administration of the U.S. Department of Energy at Los Alamos National Laboratory under Contract no. DE-AC52-06NA25396 and by Lawrence Livermore National Laboratory under Contract no. DE-AC52-07NA27344. This research was funded by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA). All statements of fact, opinion or conclusions contained herein are those of the authors and should not be constructed as representing the official views or polices of IARPA, the ODNI, or the U.S. Government. I. M. Sigal also acknowledges a support by NSERC under Grant NA 7901. M. Merkli also acknowledges a support by NSERC under Grant 205247.

References

1 Wendin G. and Shumeiko V. S., [email protected], Quantum bits with Josephson junctions, Low Temperature Physics. (2007) 33, no. 9, 724–744, 2-s2.0-0342281477, https://doi.org/10.1063/1.2780165.
10.1063/1.2780165
CAS Web of Science® Google Scholar
2 Kinion D. and [email protected], Clarke J., Microstrip superconducting quantum interference device radio-frequency amplifier: scattering parameters and input coupling, Applied Physics Letters. (2008) 92, no. 17, 3, 172503, 2-s2.0-0022161989, https://doi.org/10.1063/1.2902173.
10.1063/1.2902173
CAS Web of Science® Google Scholar
3 Makhlin Y., Schön G., and Shnirman A., Quantum-state engineering with Josephson-junction devices, Reviews of Modern Physics. (2001) 73, no. 2, 357–400, https://doi.org/10.1103/RevModPhys.73.357, 2-s2.0-0035535325.
10.1103/RevModPhys.73.357
Web of Science® Google Scholar
4 Yu Y., Han S., Chu X., Chu S.-I., and Wang Z., Coherent temporal oscillations of macroscopic quantum states in a Josephson junction, Science. (2002) 296, no. 5569, 889–892, 2-s2.0-0035943443, https://doi.org/10.1126/science.1069452.
10.1126/science.1069452
CAS PubMed Web of Science® Google Scholar
5 Devoret M. H. and [email protected], Martinis J. M., Implementing qubits with superconducting integrated circuits, Quantum Information Processing. (2004) 3, no. 1–5, 163–203, 2-s2.0-0000897035, https://doi.org/10.1007/s11128-004-3101-5.
10.1007/s11128-004-3101-5
Web of Science® Google Scholar
6 Steffen M., [email protected], Ansmann M., McDermott R. et al., State tomography of capacitively shunted phase qubits with high fidelity, Physical Review Letters. (2006) 97, no. 5, 4, 050502, 2-s2.0-28444481383, https://doi.org/10.1103/PhysRevLett.97.050502.
10.1103/PhysRevLett.97.050502
Web of Science® Google Scholar
7 Katz N., Neeley M., Ansmann M. et al., Reversal of the weak measurement of a quantum state in a superconducting phase qubit, Physical Review Letters. (2008) 101, no. 20, 4, 200401, https://doi.org/10.1103/PhysRevLett.101.200401, 2-s2.0-56249131431.
10.1103/PhysRevLett.101.200401
PubMed Web of Science® Google Scholar
8 Clerk A. A., Devoret M. H., Girvin S. M., Marquardt F., and Schoelkopf R. J., Introduction to quantum noise, measurement and amplifcation, Reviews of Modern Physics. (2010) 82, 1155–1208.
10.1103/RevModPhys.82.1155
Web of Science® Google Scholar
9 Merkli M., [email protected], Sigal I. M., and [email protected], Berman G. P., [email protected], Decoherence and thermalization, Physical Review Letters. (2007) 98, no. 13, 130401, 2-s2.0-33751021446, https://doi.org/10.1103/PhysRevLett.98.130401.
10.1103/PhysRevLett.98.130401
CAS PubMed Web of Science® Google Scholar
10 Merkli M., [email protected], Sigal I. M., and [email protected], Berman G. P., [email protected], Resonance theory of decoherence and thermalization, Annals of Physics. (2008) 323, no. 2, 373–412, 2-s2.0-0043250228, https://doi.org/10.1016/j.aop.2007.04.013.
10.1016/j.aop.2007.04.013
CAS Web of Science® Google Scholar
11 Merkli M., [email protected], Berman G. P., and [email protected], Sigal I. M., [email protected], Dynamics of collective decoherence and thermalization, Annals of Physics. (2008) 323, no. 12, 3091–3112, 2-s2.0-0035804232, https://doi.org/10.1016/j.aop.2008.07.004.
10.1016/j.aop.2008.07.004
CAS Web of Science® Google Scholar
12 Berman G. P., Kamenev D. I., and Tsifrinovich V. I., Collective decoherence of the superpositional entangled states in the quantum Shor algorithm, Physical Review A. (2005) 71, no. 3, 5, 032346, 2-s2.0-4043092517, https://doi.org/10.1103/PhysRevA.71.032346.
10.1103/PhysRevA.71.032346
Web of Science® Google Scholar
13 Dalvit D. A. R., Berman G. P., and Vishik M., Dynamics of open bosonic quantum systems in coherent state representation, Physical Review A. (2006) 73, no. 1, 013803, 2-s2.0-28844467255, https://doi.org/10.1103/PhysRevA.73.013803.
10.1103/PhysRevA.73.013803
Web of Science® Google Scholar
14 Duan L.-M. and Guo G.-C., Reducing decoherence in quantum-computer memory with all quantum bits coupling to the same environment, Physical Review A. (1998) 57, no. 2, 737–741, 2-s2.0-0000379859.
10.1103/PhysRevA.57.737
CAS Web of Science® Google Scholar
15 Joos E., Zeh H. D., Kiefer C., Giulini D., Kupsch J., and Stamatescu I. O., Decoherence and The Appearence of a Classical World in Quantum Theory, 2003, 2nd edition, Springer, Berlin, Germany, Lecture Notes in Mathematics.
10.1007/978-3-662-05328-7
Google Scholar
16 Mozyrsky D. and Privman V., Adiabatic decoherence, Journal of Statistical Physics. (1998) 91, no. 3–4, 787–799, 2-s2.0-34547303281.
10.1023/A:1023042014131
Web of Science® Google Scholar
17 Palma G. M., Suominen K.-A., and Ekert A. K., Quantum computers and dissipation, Proceedings of the Royal Society A. (1996) 452, no. 1946, 567–584, 2-s2.0-33746668224.
10.1098/rspa.1996.0029
Google Scholar
18 Shao J., Ge M.-L., and Cheng H., Decoherence of quantum-nondemolition systems, Physical Review E. (1996) 53, no. 1, 1243–1245, 2-s2.0-0000228726.
10.1103/PhysRevE.53.1243
CAS Web of Science® Google Scholar
19 Merkli M., Berman G. P., Borgonovi F., and Gebresellasie K., Evolution of entanglement of two qubits interacting through local and collective environments, Quantum Physics, preprint, http://arxiv.org/abs/1001.1144.
Google Scholar
20 Merkli M. and Starr S., A resonance theory for open quantum systems with time-dependent dynamics, Journal of Statistical Physics. (2009) 134, 871–898.
10.1007/s10955-008-9645-5
CAS Web of Science® Google Scholar
21 Bach V., Merkli M., Pedra W., and Sigal I. M., Decoherence control, in preparation.
Google Scholar
22 Breuer H.-P and Petruccione F., The Theory of Open Quantum Systems, 2002, Oxford University Press, Oxford, UK.
Google Scholar
23 Davies E. B., Markovian master equations, Communications in Mathematical Physics. (1974) 39, no. 2, 91–110, 2-s2.0-0002335432, https://doi.org/10.1007/BF01608389.
10.1007/BF01608389
Web of Science® Google Scholar
24 Davies E. B., Markovian master equations. II, Mathematische Annalen. (1976) 219, no. 2, 147–158, https://doi.org/10.1007/BF01351898, 2-s2.0-0005184869.
10.1007/BF01351898
Web of Science® Google Scholar
25 Dereziński J. and Früboes R., Fermi Golden Rule and Open Quantum Systems, 2006, 1882, Springer, Berlin, Germany, Lecture Notes in Mathematics.
Google Scholar
26 Jakšić V. and Pillet C. A., From resonances to master equations, Annales de l′Institut Henri Poincaré. (1997) 67, no. 4, 425–445.
Google Scholar
27 Merkli M., Level shift operators for open quantum systems, Journal of Mathematical Analysis and Applications. (2007) 327, no. 1, 376–399, https://doi.org/10.1016/j.jmaa.2006.04.030, 2-s2.0-33750828099.
10.1016/j.jmaa.2006.04.030
Web of Science® Google Scholar
28 Altepeter J. B., Hadley P. G., Wendelken S. M., Berglund A. J., and Kwiat P. G., [email protected], Experimental investigation of a two-qubit decoherence-free subspace, Physical Review Letters. (2004) 92, no. 14, 4, 147901, 2-s2.0-0032184559, https://doi.org/10.1103/PhysRevLett.92.147901.
10.1103/PhysRevLett.92.147901
CAS Web of Science® Google Scholar
29 Fedorov A. and Fedichkin L., [email protected], Collective decoherence of nuclear spin clusters, Journal of Physics Condensed Matter. (2006) 18, no. 12, 3217–3228, 2-s2.0-0000967082, https://doi.org/10.1088/0953-8984/18/12/005.
10.1088/0953-8984/18/12/005
CAS Web of Science® Google Scholar
30 Merkli M., [email protected], Mück M., and [email protected], Sigal I. M., Instability of equilibrium states for coupled heat reservoirs at different temperatures, Journal of Functional Analysis. (2007) 243, no. 1, 87–120, 2-s2.0-0002112903, https://doi.org/10.1016/j.jfa.2006.10.017.
10.1016/j.jfa.2006.10.017
Web of Science® Google Scholar

Citing Literature

All articles

Resonant Perturbation Theory of Decoherence and Relaxation of Quantum Bits

Abstract

1. Introduction

2. Presentation of Results