On the Mini-Superambitwistor Space and 𝒩 = 8 Super-Yang-Mills Theory
Abstract
We construct a new supertwistor space suited for establishing a Penrose-Ward transform between certain bundles over this space and solutions to the 𝒩 = 8 super-Yang-Mills equations in three dimensions. This mini-superambitwistor space is obtained by dimensional reduction of the superambitwistor space, the standard superextension of the ambitwistor space. We discuss in detail the construction of this space and its geometry before presenting the Penrose-Ward transform. We also comment on a further such transform for purely bosonic Yang-Mills-Higgs theory in three dimensions by considering third-order formal “subneighborhoods" of a miniambitwistor space.
1. Introduction and Results
A convenient way of describing solutions to a wide class of field equations has been developed using twistor geometry [1–3]. In this picture, solutions to nonlinear field equations are mapped bijectively via the Penrose-Ward transform to holomorphic structures on vector bundles over an appropriate twistor space. Such twistor spaces are well known for many theories including self-dual Yang-Mills (SDYM) theory and its supersymmetric extensions as well as 𝒩-extended full super-Yang-Mills (SYM) theories. In three dimensions, there are twistor spaces suited for describing the Bogomolny equations and their supersymmetric variants. The purpose of this paper is to fill the gaps for three-dimensional 𝒩 = 8 super-Yang-Mills theory as well as for three-dimensional Yang-Mills-Higgs theory; the cases for intermediate 𝒩 follow trivially. The idea we follow in this paper has partly been presented in [4].
Recall that the supertwistor space describing 𝒩 = 3 SDYM theory is the open subset 𝒫3|3 = ℂP3|3∖ℂP1|3; its anti-self-dual counterpart is , where the parity assignment of the appearing coordinates is simply inverted. Furthermore, we denote by 𝒫2|3 the mini-supertwistor space obtained by dimensional reduction from 𝒫3|3 and used in the description of the supersymmetric Bogomolny equations in three dimensions.
For 𝒩 = 4 SYM theory, the appropriate twistor space L5|6 is now obtained from the product upon imposing a quadric condition reducing the bosonic dimensions by one (in fact, the field theory described by L5|6 is 𝒩 = 3 SYM theory in four dimensions, which is equivalent to 𝒩 = 4 SYM theory on the level of equations of motion; in three dimensions, the same relation holds between 𝒩 = 6 and 𝒩 = 8 SYM theories). We perform an analogous construction for 𝒩 = 8 SYM theory by starting from the product of two mini-supertwistor spaces. The dimensional reduction turning the super-self-duality equations in four dimensions into the super-Bogomolny equations in three dimensions translates into a reduction of the quadric condition, which yields a constraint only to be imposed on the diagonal in the base of the vector bundle . Thus, the resulting space L4|6 is not a vector bundle but only a fibration, and the sections of this fibration form a torsion sheaf, as we will see. More explicitly, the bosonic parts of the fibers of L4|6 over are isomorphic to ℂ2 at generic points, but over the diagonal , they are isomorphic to ℂ.
As expected, we find a twistor correspondence between points in ℂ3|12 and holomorphic sections of L4|6 as well as between points in L4|6 and certain sub-supermanifolds in ℂ3|12. After introducing a real structure on L4|6, one finds a nice interpretation of the spaces involved in the twistor correspondence in terms of lines with marked points in ℝ3, which resembles the appearance of flag manifolds in the well-established twistor correspondences. Recalling that L5|6 is a Calabi-Yau supermanifold (the essential prerequisite for being the target space of a topological B-model), we are led to examine an analogous question for L4|6. The Calabi-Yau property essentially amounts to a vanishing of the first Chern class of TL5|6, which in turn encodes information about the degeneracy locus of a certain set of sections of the vector bundle . We find that the degeneracy loci of L5|6 and L4|6 are equivalent (identical up to a principal divisor).
A Penrose-Ward transform for 𝒩 = 8 SYM theory can now be conveniently established. To define the analogue of a holomorphic vector bundle over the space L4|6, we have to remember that in the Čech description, a holomorphic vector bundle is completely characterized by its transition functions, which in turn form a group-valued Čech 1-cocycle. These objects are still well defined on L4|6 and we will use such a 1-cocycle to define what we will call a pseudobundle over L4|6. In performing the transition between these pseudobundles and solutions to the 𝒩 = 8 SYM equations, care must be taken when discussing these bundles over the subset of their base. Eventually, however, one obtains a bijection between gauge equivalence classes of solutions to the 𝒩 = 8 SYM equations and equivalence classes of holomorphic pseudobundles over L4|6, which turn into holomorphically trivial vector bundles upon restriction to any holomorphic submanifold .
Considering the reduction of to the bodies of the involved spaces (i.e., putting the fermionic coordinates on all the spaces to zero), it is possible to find a twistor correspondence for certain formal neighborhoods of on which a Penrose-Ward transform for purely bosonic Yang-Mills theory in four dimensions can be built. To improve our understanding of the mini-superambitwistor space, it is also helpful to discuss the analogous construction with L4|0. We find that a third-order subthickening, (i.e., a thickening of the fibers which are only of dimension one) inside of must be considered to describe solutions to the Yang-Mills-Higgs equations in three dimensions by using pseudobundles over L4|0.
To clarify the role of the space L4|6 in detail, it would be interesting to establish a dimensionally reduced version of the construction considered by Movshev in [5]. In this paper, the author constructs a “Chern-Simons triple” consisting of a differential graded algebra (A,d) and a d-closed trace functional on a certain space ST related to the superambitwistor space. This Chern-Simons triple on ST is then conjectured to be equivalent to 𝒩 = 4 SYM theory in four dimensions. The way the construction is performed suggests a quite straightforward dimensional reduction to the case of the mini-superambitwistor space. Besides delivering a Chern-Simons triple for 𝒩 = 8 SYM theory in three dimensions, this construction would possibly shed more light on the unusual properties of the fibration L4|6.
Following Witten′s seminal paper [6], there has been growing interest in different supertwistor spaces suited as target spaces for the topological B-model (see e.g. [4, 7–14]). Although it is not clear what the topological B-model on L4|6 looks like exactly (we will present some speculations in Section 3.7), the mini-superambitwistor space might also prove to be interesting from the topological string theory point of view. In particular, the mini-superambitwistor space L4|6 is probably the mirror of the mini-supertwistor space 𝒫2|4. Maybe even the extension of infinite dimensional symmetry algebras [12] from the self-dual to the full case is easier to study in three dimensions due to the greater similarity of self-dual and full theory and the smaller number of conformal generators.
Note that we are not describing the space of null geodesics in three dimensions; this space has been constructed in [13].
The outline of this paper is as follows. In Section 2, we review the construction of the supertwistor spaces for SDYM theory and SYM theory. Furthermore, we present the dimensional reduction yielding the mini-supertwistor space used for capturing solutions to the super-Bogomolny equations. Section 3, the main part, is then devoted to deriving the mini-superambitwistor space in several ways and discussing in detail the associated twistor correspondence and its geometry. Moreover, we comment on a topological B-model on this space. In Section 4, the Penrose-Ward transform for three-dimensional 𝒩 = 8 SYM theory is presented. First, we review both the transform for 𝒩 = 4 SYM theory in four dimensions and aspects of 𝒩 = 8 SYM theory in three dimensions. Then, we introduce the pseudobundles over L4|6, which take over the role of vector bundles over the space L4|6. Eventually, we present the actual Penrose-Ward transform in detail. In the last section, we discuss the third-order subthickenings of L4|0 in , which are used in the Penrose-Ward transform for purely bosonic Yang-Mills-Higgs theory.
2. Review of Supertwistor Spaces
We will briefly review some elementary facts on supertwistor spaces and fix our conventions in this section. For a broader discussion of supertwistor and superambitwistor spaces in conventions close to the ones employed here, see [15]. For more details on the mini-supertwistor spaces, we refer to [4, 14].
2.1. Supertwistor Spaces
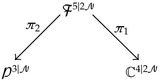 (2.5)
(2.5)The double fibration (2.5) is the foundation of the Penrose-Ward transform between equivalence classes of certain holomorphic vector bundles over 𝒫3|𝒩 and gauge equivalence classes of solutions to the 𝒩-extended supersymmetric self-dual Yang-Mills equations on ℂ4 (see e.g. [15]).
2.2. The Superambitwistor Space
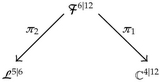 (2.14)
(2.14)Since L5|6 is a Calabi-Yau supermanifold, this space can be used as a target space for the topological B-model. However, it is still unclear what the corresponding gauge theory action will look like. The most obvious guess would be some holomorphic BF-type theory [16–18] with B a “Lagrange multiplier (0, 3)-form."
2.3. Reality Conditions on the Superambitwistor Space
On the supertwistor spaces 𝒫3|𝒩, one can define a real structure which leads to Kleinian signature on the body of the moduli space ℝ4|2𝒩 of real holomorphic sections of the fibration π2 in (2.5). Furthermore, if 𝒩 is even, one can can impose a symplectic Majorana condition which amounts to a second real structure which yields Euclidean signature. We saw above that the superambitwistor space L5|6 originates from two copies of 𝒫3|3 and, therefore, we cannot straightforwardly impose the Euclidean reality condition. However, besides the real structure leading to Kleinian signature, one can additionally define a reality condition by relating spinors of opposite helicities to each other. In this way, we obtain a Minkowski metric on the body of ℝ4|12. In the following, we will focus on the latter.
2.4. The Mini-Supertwistor Spaces
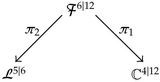 (2.30)
(2.30)The mini-supertwistor space 𝒫2|4 is again a Calabi-Yau supermanifold, and the gauge theory equivalent to the topological B-model on this space is a holomorphic BF theory [4].
3. The Mini-Superambitwistor Space
In this section, we define and examine the mini-superambitwistor space L4|6, which we will use to build a Penrose-Ward transform involving solutions to 𝒩 = 8 SYM theory in three dimensions. We will first give an abstract definition of L4|6 by a short exact sequence, and present more heuristic ways of obtaining the mini-superambitwistor space later.
3.1. Abstract Definition of the Mini-Superambitwistor Space
From the horizontal lines of this diagram and the five lemma, we conclude that . Thus, L4 is not a locally free sheaf (a more sophisticated argumentation would use the common properties of the torsion functor to establish that L4 is a torsion sheaf; furthermore, one can write down a further diagram using the nine lemma which shows that L4 is a coherent sheaf) but a torsion sheaf, whose stalks over are isomorphic to the stalks of , while the stalks over are isomorphic to the stalks of 𝒪(2, 0) ⊕ 𝒪(0, 2). Therefore, L4 is not a vector bundle, but a fibration (the homotopy lifting property typically included in the definition of a fibration is readily derived from the definition of L4) with fibers ℂ2 over generic points and fibers ℂ over . In particular, the total space of L4 is not a manifold.
The fact that the total space of the bundle L4|6 is neither a supermanifold nor a supervector bundle over seems at first slightly disturbing. However, we will show that once one is aware of this new aspect, it does not cause any deep difficulties as far as the twistor correspondence and the Penrose-Ward transform are concerned.
3.2. The Mini-Superambitwistor Space by Dimensional Reduction
3.3. Comments on Further Ways of Constructing L4|6
Although the construction presented above seems most natural, one can imagine other approaches of defining the space L4|6. Completely evident is a second way, which uses the description of L5|6 in terms of coordinates on ℱ6|12. Here, one factorizes the correspondence space ℱ6|12 by the groups generated by the vector field and obtains the correspondence space together with (3.15). A subsequent projection π2 from the dimensionally reduced correspondence space 𝒦5|12 then yields the mini-superambitwistor space L4|6 as defined above.
Furthermore, one can factorize only by 𝒢 to eliminate the dependence on one modulus. This will lead to and following the above discussion of imposing the quadric condition on the appropriate subspace, one arrives again at (3.14) and the space L4|6. Here, the quadric condition already implies the remaining factorization of by 𝒢*.
Eventually, one could anticipate the identification of moduli in (3.15) and, therefore, want to factorize by the group generated by the combination 𝒯 + 𝒯*. Acting with this sum on κ(a) will produce the sum of the results given in (3.13), and the subsequent discussion of the quadric condition follows the one presented above.
3.4. Double Fibration
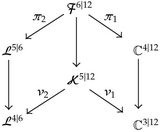 (3.16)
(3.16)3.5. Real Structure on L4|6
The reality condition τM(⋅) = ⋅ is indeed fully compatible with the condition (3.14) which reduces to L4|6. The base space of the fibration L4|6 is reduced to a single sphere S2 with real coordinates and , while the diagonal is reduced to a circle parameterized by the real coordinates . The τM-real sections of L4|6 have to satisfy . Thus, the fibers of the fibration , which are of complex dimension 2 | 6 over generic points in the base and complex dimension 1 | 6 over , are reduced to fibers of real dimension 2 | 6 and 1 | 6, respectively. In particular, note that is purely imaginary and, therefore, the quadric condition (3.14) together with the real structure τM implies that for . Thus, the body of is purely real and we have and on the diagonal .
3.6. Interpretation of the Involved Real Geometries
For the best-known twistor correspondences (i.e., the correspondence (2.5)) (more precisely, the compactified version thereof) its dual, and the correspondence (2.14), there is a nice description in terms of flag manifolds (see e.g., [3]). For the spaces involved in the twistor correspondences including minitwistor spaces, one has a similarly nice interpretation after restricting to the real situation. For simplicity, we reduce our considerations to the bodies (i.e., drop the fermionic directions) of the involved geometries, as the extension to corresponding supermanifolds is quite straightforward.
Let us first discuss the double fibration (2.30), and assume that we have imposed a suitable reality condition on the fiber coordinates, the details of which are not important. We follow again the usual discussion of the real case and leave the coordinates on the sphere complex. As correspondence space on top of the double fibration, we have thus the space ℝ3 × S2, which we can understand as the set of oriented lines (not only the ones through the origin) in ℝ3 with one marked point. Clearly, the point of such a line is given by an element of ℝ3, and the direction of this line in ℝ3 is parameterized by a point on S2. The minitwistor space 𝒫2≅𝒪(2) now is simply the space of all lines in ℝ3 [19]. Similarly to the case of flag manifolds, the projections ν1 and ν2 in (2.30) become, therefore, obvious. For ν1, simply drop the line and keep the marked point. For ν2, drop the marked point and keep the line. Equivalently, we can understand ν2 as moving the marked point on the line to its shortest possible distance from the origin. This leads to the space TS2≅𝒪(2), where the S2 parameterizes again the direction of the line, which can subsequently be still moved orthogonally to this direction, and this freedom is parameterized by the tangent planes to S2 which are isomorphic to ℝ2.
Now in the case of the fibration included in (3.16), we impose the reality condition (3.22) on the fiber coordinates of L4. In the real case, the correspondence space 𝒦5 becomes the space ℝ3 × S2 × S2 and this is the space of two oriented lines in ℝ3 intersecting in a point. More precisely, this is the space of two oriented lines in ℝ3 each with one marked point, for which the two marked points coincide. The projections ν1 and ν2 in (3.16) are then interpreted as follows. For ν1, simply drop the two lines and keep the marked point. For ν2, fix one line and move the marked point (the intersection point) together with the second line to its shortest distance to the origin. Thus, the space L4 is the space of configurations in ℝ3, in which a line has a common point with another line at its shortest distance to the origin.
Let us summarize all the above findings in Table 1.
| Space | Relation to ℝ3 |
|---|---|
| ℝ3 | marked points in ℝ3 |
| ℝ3 × S2 | oriented lines with a marked point in ℝ3 |
| 𝒫2≅𝒪(2) | oriented lines in ℝ3 (with a marked point at shortest distance to the origin.) |
| ℝ3 × S2 × S2 | two oriented lines with a common marked point in ℝ3 |
| L4 | two oriented lines with a common marked point at shortest distance from one of the lines to the origin in ℝ3 |
3.7. Remarks Concerning a Topological B-Model on L4|6
The space L4|6 is not well suited as a target space for a topological B-model since it is not a (Calabi-Yau) manifold. However, one clearly expects that it is possible to define an analogous model since, if we assume that the conjecture in [20, 21] is correct, such a model should simply be the mirror of the minitwistor string theory considered in [14]. This model would furthermore yield some holomorphic Chern-Simons type equations of motion. The latter equations would then define holomorphic pseudobundles over L4|6 by an analogue of a holomorphic structure. These bundles will be introduced in Section 4.3 and in our discussion, they substitute the holomorphic vector bundles.
Interestingly, the space L4|6 has a property which comes close to vanishing of a first Chern class. Recall that for any complex vector bundle, its Chern classes are Poincaré dual to the degeneracy cycles of certain sets of sections (this is a Gauß-Bonnet formula). More precisely, to calculate the first Chern class of a rank r vector bundle, one considers r generic sections and arranges them into an r × r matrix L. The degeneracy loci on the base space are then given by the zero locus of det (L). Clearly, this calculation can be translated directly to L4|6.
When dealing with degenerated twistor spaces, one usually retreats to the correspondence space endowed with some additional symmetry conditions [22]. It is conceivable that a similar procedure will help to define the topological B-model in our case. Also, defining a suitable blowup of L4|6 over could be the starting point for finding an appropriate action.
4. The Penrose-Ward Transform for the Mini-Superambitwistor Space
4.1. Review of the Penrose-Ward Transform on the Superambitwistor Space
We thus showed that there is a correspondence between certain holomorphic structures on L5|6, holomorphic vector bundles over L5|6 which become holomorphically trivial when restricted to certain subspaces and solutions to the 𝒩 = 4 SYM equations on ℂ4. The redundancy in each set of objects is modded out by considering gauge equivalence classes and holomorphic equivalence classes of vector bundles, which renders the above correspondences one-to-one.
4.2. 𝒩 = 8 SYM Theory in Three Dimension
This theory is obtained by dimensionally reducing 𝒩 = 1 SYM theory in ten dimensions to three dimensions, or, equivalently, by dimensionally reducing four-dimensional 𝒩 = 4 SYM theory to three dimensions. As a result, the 16 real supercharges are rearranged in the latter case from four spinors transforming as a 2ℂ of Spin(3, 1)≅SL(2, ℂ) into eight spinors transforming as a 2ℝ of Spin(2, 1)≅SL(2, ℝ).
The automorphism group of the supersymmetry algebra is Spin(8), and the little group of the remaining Lorentz group SO(2, 1) is trivial. As massless particle content, we, therefore, expect bosons transforming in the 8v and fermions transforming in the 8c of Spin(8). One of the bosons will, however, appear as a dual gauge potential on ℝ3 after dimensional reduction, and, therefore, only a Spin(7) R-symmetry group is manifest in the action and the equations of motion. In the mini-superambitwistor formulation, the manifest subgroup of the R-symmetry group is only SU(3) × U(1) × SU(3) × U(1). Altogether, we have a gauge potential Aμ with μ = 1, …,3, seven scalars ϕi with i = 1, …,7, and eight spinors with j = 1, …,8.
Moreover, recall that in four dimensions, 𝒩 = 3 and 𝒩 = 4 super-Yang-Mills theories are equivalent on the level of field content and corresponding equations of motion. The only difference is found in the manifest R-symmetry groups which are SU(3) × U(1) and SU(4), respectively. This equivalence obviously carries over to the three-dimensional situation. 𝒩 = 6 and 𝒩 = 8 super-Yang-Mills theories are equivalent regarding their field content and the equations of motion. Therefore, it is sufficient to construct a twistor correspondence for 𝒩 = 6 SYM theory to describe solutions to the 𝒩 = 8 SYM equations.
4.3. Pseudobundles over L4|6
Because the mini-superambitwistor space is only a fibration and not a manifold, there is no notion of holomorphic vector bundles over L4|6. However, our space is close enough to a manifold to translate all the necessary terms in a simple manner.
Let us fix the covering 𝔘 of the total space of the fibration L4|6 to be given by the patches 𝒱(a) introduced above. Furthermore, define 𝔖 to be the sheaf of smooth GL(n, ℂ)-valued functions on L4|6 and ℌ to be its subsheaf consisting of holomorphic GL(n, ℂ)-valued functions on L4|6, i.e. smooth and holomorphic functions which depend only on the coordinates given in (3.12) and λ(a), μ(a).
We define a complex pseudo-bundle over L4|6 of rank n by a Čech 1-cocycle {fab} ∈ Ž1(𝔘, 𝔖) on L4|6 in full analogy with transition functions defining ordinary vector bundles. If the 1-cocycle is an element of Ž1(𝔘, ℌ), we speak of a holomorphic pseudo-bundle over L4|6. Two pseudo-bundles given by Čech 1-cocycles {fab} and are called topologically equivalent (holomorphically equivalent), if there is a Čech 0-cochain {ψa} ∈ Č0(𝔘, 𝔖) (a Čech 0-cochain {ψa} ∈ Č0(𝔘, ℌ)) such that . A pseudo-bundle is called trivial (holomorphically trivial), if it is topologically equivalent (holomorphically equivalent) to the trivial pseudo-bundle given by {fab} = {⊮ab}.
In the corresponding discussion of Čech cohomology on ordinary manifolds, one can achieve independence of the covering if the patches of the covering are all Stein manifolds. An analogous argument should also be applicable here, but for our purposes, it is enough to restrict to the covering 𝔘.
Besides the Čech description, it is also possible to introduce an equivalent Dolbeault description, which will, however, demand an extended notion of Dolbeault cohomology classes.
4.4. The Penrose-Ward Transform Using the Mini-Superambitwistor Space
With the double fibration contained in (3.16), it is not hard to establish the corresponding Penrose-Ward transform, which is essentially a dimensional reduction of the four-dimensional case presented in Section 4.1.
To sum up, we obtained a correspondence between holomorphic pseudobundles over L4|6 which become holomorphically trivial vector bundles upon reduction to any subspace and solutions to the three-dimensional 𝒩 = 8 SYM equations. As this correspondence arises by a dimensional reduction of a correspondence which is one-to-one, it is rather evident that also in this case, we have a bijection between both the holomorphic pseudobundles over L4|6 and the solutions after factoring out holomorphic equivalence and gauge equivalence, respectively.
5. Purely Bosonic Yang-Mills-Higgs Theory from Third-order Subneighborhoods
In this section, we want to turn to the purely bosonic situation (in other words, all the superspaces used up to now loose their Graßmann-odd dimensions) and describe solutions to the three-dimensional Yang-Mills-Higgs equations using a mini-ambitwistor space (when speaking about Yang-Mills-Higgs theory, we mean a theory without quartic interaction term). That is, we will consider the dimensional reduction of the purely bosonic case discussed in [23, 24] from d = 4 to d = 3. In these papers, it has been shown that solutions to the Yang-Mills field equations are equivalent to holomorphic vector bundles over a third-order thickening of the ambitwistor space L5 in .
5.1. Thickenings of Complex Manifolds
Note that it is easily possible to map L5|6 to a third-order thickening of by identifying the nilpotent even coordinate y with 2θiηi (cf. [27]). However, we will not follow this approach for two reasons. First, the situation is more subtle in the case of L4|6 since L4 only allows for a nilpotent even direction inside for λ± = μ±. Second, this description has several drawbacks when the discussion of the Penrose-Ward transform reaches the correspondence space, where the concepts of thickenings (and the extended fattenings) are not sufficient (see [27]).
5.2. Third-Order Thickenings and d = 4 Yang-Mills Theory
Altogether, we see that a solution to the Yang-Mills equations corresponds to a topologically trivial holomorphic vector bundle over a third-order thickening of L5 in , which becomes holomorphically trivial, when restricted to any .
5.3. Third-Order Subthickenings and d = 3 Yang-Mills-Higgs Theory
Thus, solutions to the Yang-Mills-Higgs equations (5.9) correspond to solutions to (5.15) on ℂ3 × ℂ3. Recall that solutions to the first two equations of (5.15) correspond in the twistor description to holomorphic vector bundles over . Furthermore, the expansion of the gauge potential (5.16) is an expansion in a second-order infinitesimal neighborhood of diag(ℂ3 × ℂ3). As we saw in the construction of the mini-superambitwistor space L4|6, the diagonal for which corresponds to . The neighborhoods of this diagonal will then correspond to subthickenings of L4 inside , that is, for μ± = λ±, we have the additional nilpotent coordinate ξ. In other words, the subthickening of L4 in is obtained by turning one of the fiber coordinates of 𝒫2 × 𝒫2 over into a nilpotent even coordinate (in a suitable basis). Then, we can finally state the following:
Gauge equivalence classes of solutions to the three-dimensional Yang-Mills-Higgs equations are in one-to-one correspondence with gauge equivalence classes of holomorphic pseudobundles over a third-order subthickening of L4, which become holomorphically trivial vector bundles when restricted to a ℂP1 × ℂP1 holomorphically embedded into L4.
Acknowledgments
The author would like to thank Alexander Popov, Sebastian Uhlmann, and Martin Wolf for numerous helpful discussions and comments on a draft of this paper. Furthermore, he is grateful to Klaus Hulek for a discussion on the geometry of the mini-superambitwistor space L4|6. This work was done within the framework of the DFG priority program (SPP 1096) in string theory.




