Modeling a Quantum Hall System via Elliptic Equations
Abstract
Quantum Hall systems are a suitable theme for a case study in the general area of nanotechnology. In particular, it is a good framework to search for universal principles relevant to nanosystem modeling and nanosystem-specific signal processing. Recently, we have been able to construct a partial differential equations-based model of a quantum Hall system, which consists of the Schrödinger equation supplemented with a special-type nonlinear feedback loop. This result stems from a novel theoretical approach, which in particular brings to the fore the notion of quantum information. Here we undertake to modify the original model by substituting the dynamics based on the Dirac operator. This leads to a model that consists of a system of three nonlinearly coupled first-order elliptic equations in the plane.
1. Quantum Entanglement of Composite Systems and Its Associated Hamiltonian Dynamics
In this section, we give a very brief overview of the principles behind the mesoscopic loop models as developed in [1–5]. The theme of quantum information is extremely relevant to our approach, but it has been brought to light in explicit terms only recently; an in-depth discussion will appear elsewhere [6, 7].
2. The Mesoscopic-Loop Model Based on the Dirac-Type Equations
3. Quantization of Hall Resistance
4. The Elliptic System in the Plane
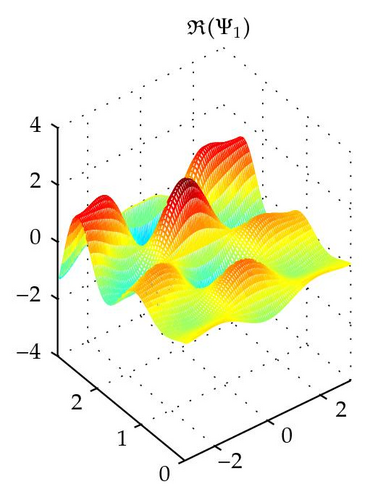
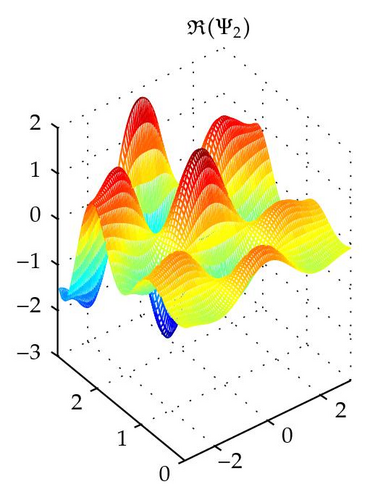
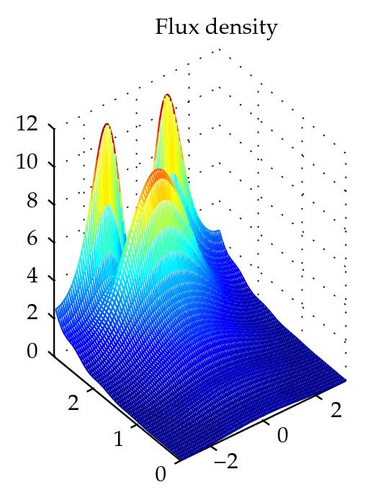
5. Closing Comments
The Dirac equation is undergoing a renaissance in condensed matter physics due to its relevance to the unusual two-dimensional crystal called graphene (see, e.g., [13]). I emphasize that in this paper we have not addressed any of the issues related to that stream of research. Rather, we have used the Dirac equation as an analytic alternative to the Schrödiner equation. It helped us find an almost equivalent reformulation of the nonrelativistic model.
Acknowledgment
The author is grateful to the journal referees whose thoughtful questions and comments helped improve this paper.




